高中数学苏教版(2022春 )选择性必修第二册 §7.4 第3课时 二项式系数的性质(63张PPT)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 §7.4 第3课时 二项式系数的性质(63张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览










文档简介
(共63张PPT)
第3课时 二项式系数的性质
第7章 §7.4 二项式定理
1.了解二项式系数的性质.
2.理解二项式系数性质的应用.
3.掌握应用“赋值法”.
学习目标
被誉为“世界七大奇迹”之一的古埃及的金字塔,以其宏伟的气势、严密的结构、精美绝伦的整体外观让世界叹服.而数学上也有“金字塔”,这就是二项式(a+b)n的展开式在n=1,2,…时的二项式系数而垒成的金字塔,称为杨辉三角,它是我国南宋数学家杨辉首先发现的,比欧洲的帕斯卡整整早发现了500年左右.
导语
随堂演练
课时对点练
一、二项式系数表
二、二项式系数的对称性、增减性、最值
三、二项展开式的系数和问题
内容索引
一、二项式系数表
问题1 根据二项式定理写出(a+b)n(n=1,2,3,4,5,6)的二项式系数.可以写成如下形式,则第7行的数字分别是多少?
提示 1,7,21,35,35,21,7,1.
知识梳理
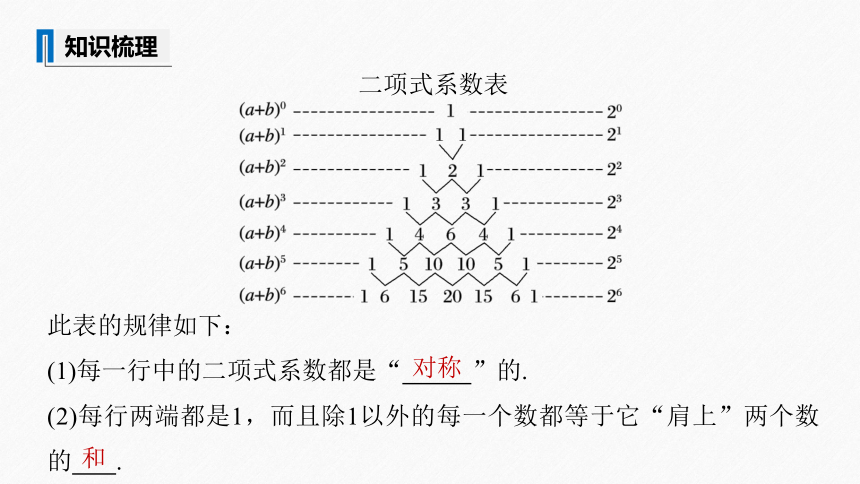
二项式系数表
此表的规律如下:
(1)每一行中的二项式系数都是“ ”的.
(2)每行两端都是1,而且除1以外的每一个数都等于它“肩上”两个数的 .
对称
和
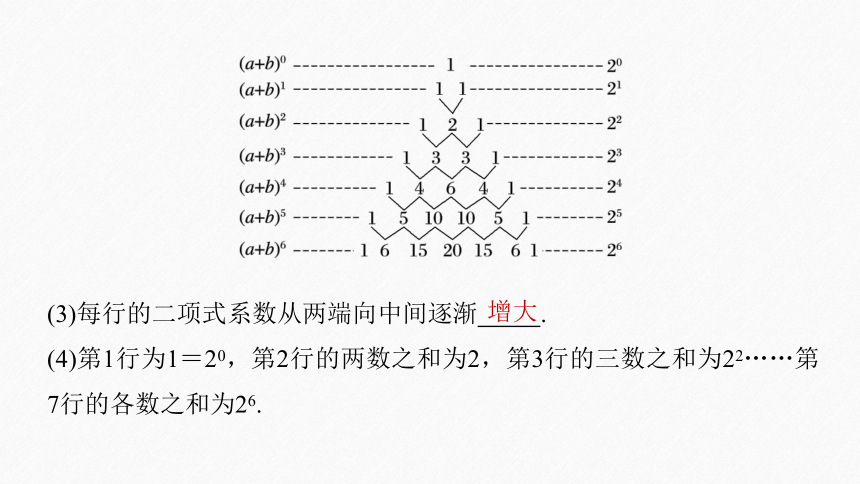
(3)每行的二项式系数从两端向中间逐渐 .
(4)第1行为1=20,第2行的两数之和为2,第3行的三数之和为22……第7行的各数之和为26.
增大
例1 如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:1,2,3,3,6,4,10,5,…,记其前n项和为Sn,求S16的值.
解 由题意及二项式系数表的特点可得
S16=(1+2)+(3+3)+(6+4)+(10+5)+…+(36+9)
=164.
反思感悟 解决与杨辉三角有关问题的一般思路
(1)观察:对题目要横看、竖看、隔行看、连续看,多角度观察.
(2)找规律:通过观察找出每一行的数之间,行与行之间的数据的规律.
(3)将数据间的这种联系用数学式表达出来,使问题得解.
跟踪训练1 如图是与杨辉三角有类似性质的三角形数垒,a,b是某行的前两个数,当a=7时,b等于
A.20 B.21
C.22 D.23
√
解析 由a=7,可知b左肩上的数为6,右肩上的数为11+5,即16,所以b=6+16=22.
二、二项式系数的对称性、增减性、最值
问题2 怎样找二项展开式中的二项式系数的最大值?
知识梳理
二项式系数的对称性、增减性、最值
例2 (1+2x)n展开式第6项与第7项的系数相等,求展开式中二项式系数最大的项.
解得n=8.
反思感悟 求二项式系数的最大项,根据二项式系数的性质对(a+b)n中的n进行讨论.
(1)当n为奇数时,中间两项的二项式系数最大;
(2)当n为偶数时,中间一项的二项式系数最大.
跟踪训练2 (1-x)2n-1展开式中,二项式系数最大的项是
A.第n-1项
B.第n项
C.第n-1项与第n+1项
D.第n项与第n+1项
√
解析 由二项式系数的性质得,二项式系数最大为
分别为第n,n+1项.
三、二项展开式的系数和问题
知识梳理
二项式系数的和
2n
2n-1
例3 已知(2x-1)5=a0x5+a1x4+a2x3+a3x2+a4x+a5.求下列各式的值:
(1)a0+a1+a2+…+a5;
解 令x=1,
得a0+a1+a2+…+a5=1.
(2)|a0|+|a1|+|a2|+…+|a5|;
解 令x=-1,得-35=-a0+a1-a2+a3-a4+a5.
知a1,a3,a5为负值,
所以|a0|+|a1|+|a2|+…+|a5|=a0-a1+a2-a3+a4-a5=35=243.
(3)a1+a3+a5.
解 由a0+a1+a2+…+a5=1,
-a0+a1-a2+…+a5=-35,
得2(a1+a3+a5)=1-35,
延伸探究 在本例条件下,求下列各式的值:
(1)a0+a2+a4;
解 因为a0+a1+a2+…+a5=1,
-a0+a1-a2+…+a5=-35.
(2)a1+a2+a3+a4+a5;
解 因为a0是(2x-1)5的展开式中x5的系数,
所以a0=25=32.
又a0+a1+a2+…+a5=1,
所以a1+a2+a3+a4+a5=-31.
(3)5a0+4a1+3a2+2a3+a4.
解 因为(2x-1)5=a0x5+a1x4+a2x3+a3x2+a4x+a5,
所以两边求导数得
10(2x-1)4=5a0x4+4a1x3+3a2x2+2a3x+a4.
令x=1,得5a0+4a1+3a2+2a3+a4=10.
反思感悟 二项展开式中系数和的求法
(1)对形如(ax+b)n,(ax2+bx+c)m(a,b,c∈R,m,n∈N*)的式子求其展开式的各项系数之和,常用赋值法,只需令x=1即可,对(ax+by)n(a,b∈R,n∈N*)的式子求其展开式的各项系数之和,只需令x=y=1即可.
(2)一般地,若f(x)=a0+a1x+a2x2+…+anxn,则f(x)展开式中各项系数之和为f(1),
跟踪训练3 已知(x2-2x-3)10=a0+a1(x-1)+a2(x-1)2+…+a20(x-1)20.
(1)求a2的值;
解 ∵(x2-2x-3)10=a0+a1(x-1)+a2(x-1)2+…+a20(x-1)20,令x-1=t,
展开式化为(t2-4)10=a0+a1t+a2t2+…+a20t20.
(2)求a1+a3+a5+…+a19的值;
解 令t=1,得a0+a1+a2+…+a20=310,
令t=-1,得a0-a1+a2-…+a20=310,
∴a1+a3+a5+…+a19=0.
(3)求a0+a2+a4+…+a20的值.
解 由(2)得a0+a2+a4+…+a20=310.
1.知识清单:
(1)二项式系数表.
(2)二项式系数的增减性与最值.
(3)二项展开式的系数和问题.
2.方法归纳:赋值法,整体运算.
3.常见误区:系数与二项式系数的区别,中间项的个数,含绝对值的系数.
课堂小结
随堂演练
1.观察图中的数所成的规律,则a所表示的数是
1
2
3
4
A.8 B.6 C.4 D.2
√
解析 由题图知,下一行的数是其肩上两数的和,
所以4+a=10,得a=6.
1
2
3
4
2.在(a-b)20的展开式中,与第6项二项式系数相同的项是
A.第15项 B.第16项
C.第17项 D.第18项
√
1
2
3
4
A.第5项 B.第6项 C.第7项 D.第8项
√
√
1
2
3
4
4.(2x-1)6的展开式中各项系数的和为__;各项的二项式系数的和为___.
1
解析 令x=1,得各项系数的和为1;各二项式系数之和为26=64.
64
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1.在(a+b)n的二项展开式中,与第k项的二项式系数相同的项是
A.第n-k项 B.第n-k-1项
C.第n-k+1项 D.第n-k+2项
16
√
2.已知(1+x)n的展开式中只有第6项的二项式系数最大,则展开式中的奇数项的二项式系数之和为
A.212 B.211 C.210 D.29
解析 ∵展开式中只有第6项的二项式系数最大,
∴n=10,
∵奇数项的二项式系数之和等于偶数项的二项式系数之和,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(1+x)+(1+x)2+…+(1+x)n的展开式中各项系数之和为
A.2n+1 B.2n-1
C.2n+1-1 D.2n+1-2
√
解析 令x=1,则2+22+…+2n=2n+1-2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.在(x+y)n的展开式中,第4项与第8项的系数相等,则展开式中系数最大的项是
A.第6项 B.第5项 C.第5,6项 D.第6,7项
√
∴展开式中二项式系数最大的项为第6项,它也是系数最大的项.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(多选)关于(a-b)11的说法,正确的是
A.展开式中的二项式系数之和为2 048
B.展开式中只有第6项的二项式系数最大
C.展开式中第6项和第7项的二项式系数最大
D.展开式中第6项的系数最大
√
√
解析 (a-b)11的展开式中的二项式系数之和为211=2 048,故A正确;
因为n=11为奇数,所以展开式中有12项,中间两项(第6项和第7项)的二项式系数相等且最大,故B不正确,C正确;
展开式中第6项的系数为负数,不是最大值,故D不正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知(x-1)n的展开式中奇数项的二项式系数之和是64,则
A.n=7 B.所有项的系数和为0
C.偶数项的系数和为-64 D.展开式的中间项为-35x3和35x4
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10
故n=5.
令10-5r=0,得r=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
34
8.如图,在由二项式系数所构成的杨辉三角中,第____行中从左至右的第14个数与第15个数的比为2∶3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.设(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,求:
(1)a1+a2+a3+a4;
解 由(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,
令x=1,得(2-3)4=a0+a1+a2+a3+a4,
令x=0,得(0-3)4=a0,
所以a1+a2+a3+a4=a0+a1+a2+a3+a4-a0
=(2-3)4-81=-80.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)(a0+a2+a4)2-(a1+a3)2;
解 在(2x-3)4=a0+a1x+a2x2+a3x3+a4x4中,
令x=1,得(2-3)4=a0+a1+a2+a3+a4. ①
令x=-1,得(-2-3)4=a0-a1+a2-a3+a4. ②
所以(a0+a2+a4)2-(a1+a3)2
=(a0-a1+a2-a3+a4)(a0+a1+a2+a3+a4)
=(-2-3)4(2-3)4=(2+3)4(2-3)4=625.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)|a1|+|a2|+|a3|+|a4|.
解 由展开式知a0,a2,a4为正,a1,a3为负,
由(2)中①+②得2(a0+a2+a4)=626,
由(2)中①-②得2(a1+a3)=-624,
所以|a1|+|a2|+|a3|+|a4|=-a1+a2-a3+a4
=(a0+a2+a4)-(a1+a3)-a0
=313+312-81=544.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求m,n的值;
解 由题意可得2n=256,解得n=8,
解得m=2或m=-2(舍去).
故m,n的值分别为2,8.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求展开式中偶数项的二项式系数之和;
解 展开式中偶数项的二项式系数之和为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.若x10=a0+a1(x-1)+a2(x-1)2+…+a10(x-1)10,则a8的值为
A.10 B.45 C.-9 D.-45
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.2 B.0 C.-2 D.-1
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.462 B.400 C.390 D.300
√
∵二项式的展开式中所有项的二项式系数和为2n,而所有偶数项的二项式系数和与所有奇数项的二项式系数和相等,故由题意得2n-1=1 024,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.(多选)传说古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.这是因为阿基米德认为这个“圆柱容球”是他最为得意的发现,于是留下遗言:他死后,墓碑上要刻上一个“圆柱容球”的几何图形,设圆柱的体积与球的体积之比为m,圆柱的表面积与球的表面积之比为n,若f(x)= ,则
A.f(x)的展开式中的常数项是56
B.f(x)的展开式中的各项系数之和为0
C.f(x)的展开式中的二项式系数最大值是70
D.f(i)=-16,其中i为虚数单位
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设内切球的半径为r,则圆柱的高为2r,
对于A,f(x)展开式通项公式为
令24-4r=0,解得r=6,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于B,f(1)=0,即f(x)展开式的各项系数之和为0,B正确;
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.杨辉三角是杨辉的一项重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律,如图是一个11阶杨辉三角:
(1)求第20行中从左到右的第4个数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)在第2斜列中,前5个数依次为1,3,6,10,15,在第3斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m-1斜列中(从右上到左下)前k个数之和,一定等于第m斜列中第k个数.
试用含有m,k(m,k∈N*)的数字公式表示上述结论,并给予证明.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明如下:
=右边.
本课结束
第3课时 二项式系数的性质
第7章 §7.4 二项式定理
1.了解二项式系数的性质.
2.理解二项式系数性质的应用.
3.掌握应用“赋值法”.
学习目标
被誉为“世界七大奇迹”之一的古埃及的金字塔,以其宏伟的气势、严密的结构、精美绝伦的整体外观让世界叹服.而数学上也有“金字塔”,这就是二项式(a+b)n的展开式在n=1,2,…时的二项式系数而垒成的金字塔,称为杨辉三角,它是我国南宋数学家杨辉首先发现的,比欧洲的帕斯卡整整早发现了500年左右.
导语
随堂演练
课时对点练
一、二项式系数表
二、二项式系数的对称性、增减性、最值
三、二项展开式的系数和问题
内容索引
一、二项式系数表
问题1 根据二项式定理写出(a+b)n(n=1,2,3,4,5,6)的二项式系数.可以写成如下形式,则第7行的数字分别是多少?
提示 1,7,21,35,35,21,7,1.
知识梳理
二项式系数表
此表的规律如下:
(1)每一行中的二项式系数都是“ ”的.
(2)每行两端都是1,而且除1以外的每一个数都等于它“肩上”两个数的 .
对称
和
(3)每行的二项式系数从两端向中间逐渐 .
(4)第1行为1=20,第2行的两数之和为2,第3行的三数之和为22……第7行的各数之和为26.
增大
例1 如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:1,2,3,3,6,4,10,5,…,记其前n项和为Sn,求S16的值.
解 由题意及二项式系数表的特点可得
S16=(1+2)+(3+3)+(6+4)+(10+5)+…+(36+9)
=164.
反思感悟 解决与杨辉三角有关问题的一般思路
(1)观察:对题目要横看、竖看、隔行看、连续看,多角度观察.
(2)找规律:通过观察找出每一行的数之间,行与行之间的数据的规律.
(3)将数据间的这种联系用数学式表达出来,使问题得解.
跟踪训练1 如图是与杨辉三角有类似性质的三角形数垒,a,b是某行的前两个数,当a=7时,b等于
A.20 B.21
C.22 D.23
√
解析 由a=7,可知b左肩上的数为6,右肩上的数为11+5,即16,所以b=6+16=22.
二、二项式系数的对称性、增减性、最值
问题2 怎样找二项展开式中的二项式系数的最大值?
知识梳理
二项式系数的对称性、增减性、最值
例2 (1+2x)n展开式第6项与第7项的系数相等,求展开式中二项式系数最大的项.
解得n=8.
反思感悟 求二项式系数的最大项,根据二项式系数的性质对(a+b)n中的n进行讨论.
(1)当n为奇数时,中间两项的二项式系数最大;
(2)当n为偶数时,中间一项的二项式系数最大.
跟踪训练2 (1-x)2n-1展开式中,二项式系数最大的项是
A.第n-1项
B.第n项
C.第n-1项与第n+1项
D.第n项与第n+1项
√
解析 由二项式系数的性质得,二项式系数最大为
分别为第n,n+1项.
三、二项展开式的系数和问题
知识梳理
二项式系数的和
2n
2n-1
例3 已知(2x-1)5=a0x5+a1x4+a2x3+a3x2+a4x+a5.求下列各式的值:
(1)a0+a1+a2+…+a5;
解 令x=1,
得a0+a1+a2+…+a5=1.
(2)|a0|+|a1|+|a2|+…+|a5|;
解 令x=-1,得-35=-a0+a1-a2+a3-a4+a5.
知a1,a3,a5为负值,
所以|a0|+|a1|+|a2|+…+|a5|=a0-a1+a2-a3+a4-a5=35=243.
(3)a1+a3+a5.
解 由a0+a1+a2+…+a5=1,
-a0+a1-a2+…+a5=-35,
得2(a1+a3+a5)=1-35,
延伸探究 在本例条件下,求下列各式的值:
(1)a0+a2+a4;
解 因为a0+a1+a2+…+a5=1,
-a0+a1-a2+…+a5=-35.
(2)a1+a2+a3+a4+a5;
解 因为a0是(2x-1)5的展开式中x5的系数,
所以a0=25=32.
又a0+a1+a2+…+a5=1,
所以a1+a2+a3+a4+a5=-31.
(3)5a0+4a1+3a2+2a3+a4.
解 因为(2x-1)5=a0x5+a1x4+a2x3+a3x2+a4x+a5,
所以两边求导数得
10(2x-1)4=5a0x4+4a1x3+3a2x2+2a3x+a4.
令x=1,得5a0+4a1+3a2+2a3+a4=10.
反思感悟 二项展开式中系数和的求法
(1)对形如(ax+b)n,(ax2+bx+c)m(a,b,c∈R,m,n∈N*)的式子求其展开式的各项系数之和,常用赋值法,只需令x=1即可,对(ax+by)n(a,b∈R,n∈N*)的式子求其展开式的各项系数之和,只需令x=y=1即可.
(2)一般地,若f(x)=a0+a1x+a2x2+…+anxn,则f(x)展开式中各项系数之和为f(1),
跟踪训练3 已知(x2-2x-3)10=a0+a1(x-1)+a2(x-1)2+…+a20(x-1)20.
(1)求a2的值;
解 ∵(x2-2x-3)10=a0+a1(x-1)+a2(x-1)2+…+a20(x-1)20,令x-1=t,
展开式化为(t2-4)10=a0+a1t+a2t2+…+a20t20.
(2)求a1+a3+a5+…+a19的值;
解 令t=1,得a0+a1+a2+…+a20=310,
令t=-1,得a0-a1+a2-…+a20=310,
∴a1+a3+a5+…+a19=0.
(3)求a0+a2+a4+…+a20的值.
解 由(2)得a0+a2+a4+…+a20=310.
1.知识清单:
(1)二项式系数表.
(2)二项式系数的增减性与最值.
(3)二项展开式的系数和问题.
2.方法归纳:赋值法,整体运算.
3.常见误区:系数与二项式系数的区别,中间项的个数,含绝对值的系数.
课堂小结
随堂演练
1.观察图中的数所成的规律,则a所表示的数是
1
2
3
4
A.8 B.6 C.4 D.2
√
解析 由题图知,下一行的数是其肩上两数的和,
所以4+a=10,得a=6.
1
2
3
4
2.在(a-b)20的展开式中,与第6项二项式系数相同的项是
A.第15项 B.第16项
C.第17项 D.第18项
√
1
2
3
4
A.第5项 B.第6项 C.第7项 D.第8项
√
√
1
2
3
4
4.(2x-1)6的展开式中各项系数的和为__;各项的二项式系数的和为___.
1
解析 令x=1,得各项系数的和为1;各二项式系数之和为26=64.
64
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1.在(a+b)n的二项展开式中,与第k项的二项式系数相同的项是
A.第n-k项 B.第n-k-1项
C.第n-k+1项 D.第n-k+2项
16
√
2.已知(1+x)n的展开式中只有第6项的二项式系数最大,则展开式中的奇数项的二项式系数之和为
A.212 B.211 C.210 D.29
解析 ∵展开式中只有第6项的二项式系数最大,
∴n=10,
∵奇数项的二项式系数之和等于偶数项的二项式系数之和,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.(1+x)+(1+x)2+…+(1+x)n的展开式中各项系数之和为
A.2n+1 B.2n-1
C.2n+1-1 D.2n+1-2
√
解析 令x=1,则2+22+…+2n=2n+1-2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.在(x+y)n的展开式中,第4项与第8项的系数相等,则展开式中系数最大的项是
A.第6项 B.第5项 C.第5,6项 D.第6,7项
√
∴展开式中二项式系数最大的项为第6项,它也是系数最大的项.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(多选)关于(a-b)11的说法,正确的是
A.展开式中的二项式系数之和为2 048
B.展开式中只有第6项的二项式系数最大
C.展开式中第6项和第7项的二项式系数最大
D.展开式中第6项的系数最大
√
√
解析 (a-b)11的展开式中的二项式系数之和为211=2 048,故A正确;
因为n=11为奇数,所以展开式中有12项,中间两项(第6项和第7项)的二项式系数相等且最大,故B不正确,C正确;
展开式中第6项的系数为负数,不是最大值,故D不正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知(x-1)n的展开式中奇数项的二项式系数之和是64,则
A.n=7 B.所有项的系数和为0
C.偶数项的系数和为-64 D.展开式的中间项为-35x3和35x4
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10
故n=5.
令10-5r=0,得r=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
34
8.如图,在由二项式系数所构成的杨辉三角中,第____行中从左至右的第14个数与第15个数的比为2∶3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.设(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,求:
(1)a1+a2+a3+a4;
解 由(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,
令x=1,得(2-3)4=a0+a1+a2+a3+a4,
令x=0,得(0-3)4=a0,
所以a1+a2+a3+a4=a0+a1+a2+a3+a4-a0
=(2-3)4-81=-80.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)(a0+a2+a4)2-(a1+a3)2;
解 在(2x-3)4=a0+a1x+a2x2+a3x3+a4x4中,
令x=1,得(2-3)4=a0+a1+a2+a3+a4. ①
令x=-1,得(-2-3)4=a0-a1+a2-a3+a4. ②
所以(a0+a2+a4)2-(a1+a3)2
=(a0-a1+a2-a3+a4)(a0+a1+a2+a3+a4)
=(-2-3)4(2-3)4=(2+3)4(2-3)4=625.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)|a1|+|a2|+|a3|+|a4|.
解 由展开式知a0,a2,a4为正,a1,a3为负,
由(2)中①+②得2(a0+a2+a4)=626,
由(2)中①-②得2(a1+a3)=-624,
所以|a1|+|a2|+|a3|+|a4|=-a1+a2-a3+a4
=(a0+a2+a4)-(a1+a3)-a0
=313+312-81=544.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求m,n的值;
解 由题意可得2n=256,解得n=8,
解得m=2或m=-2(舍去).
故m,n的值分别为2,8.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求展开式中偶数项的二项式系数之和;
解 展开式中偶数项的二项式系数之和为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.若x10=a0+a1(x-1)+a2(x-1)2+…+a10(x-1)10,则a8的值为
A.10 B.45 C.-9 D.-45
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.2 B.0 C.-2 D.-1
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.462 B.400 C.390 D.300
√
∵二项式的展开式中所有项的二项式系数和为2n,而所有偶数项的二项式系数和与所有奇数项的二项式系数和相等,故由题意得2n-1=1 024,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.(多选)传说古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.这是因为阿基米德认为这个“圆柱容球”是他最为得意的发现,于是留下遗言:他死后,墓碑上要刻上一个“圆柱容球”的几何图形,设圆柱的体积与球的体积之比为m,圆柱的表面积与球的表面积之比为n,若f(x)= ,则
A.f(x)的展开式中的常数项是56
B.f(x)的展开式中的各项系数之和为0
C.f(x)的展开式中的二项式系数最大值是70
D.f(i)=-16,其中i为虚数单位
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设内切球的半径为r,则圆柱的高为2r,
对于A,f(x)展开式通项公式为
令24-4r=0,解得r=6,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
对于B,f(1)=0,即f(x)展开式的各项系数之和为0,B正确;
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.杨辉三角是杨辉的一项重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律,如图是一个11阶杨辉三角:
(1)求第20行中从左到右的第4个数;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)在第2斜列中,前5个数依次为1,3,6,10,15,在第3斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m-1斜列中(从右上到左下)前k个数之和,一定等于第m斜列中第k个数.
试用含有m,k(m,k∈N*)的数字公式表示上述结论,并给予证明.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
证明如下:
=右边.
本课结束
