高中数学苏教版(2022春 )选择性必修第二册 第7章 计数原理 章末复习课(57张PPT)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 第7章 计数原理 章末复习课(57张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 15:51:57 | ||
图片预览











文档简介
(共48张PPT)
章末复习课
第7章 计数原理
一、两个计数原理
二、排列与组合的综合应用
三、二项式定理及其应用
内容索引
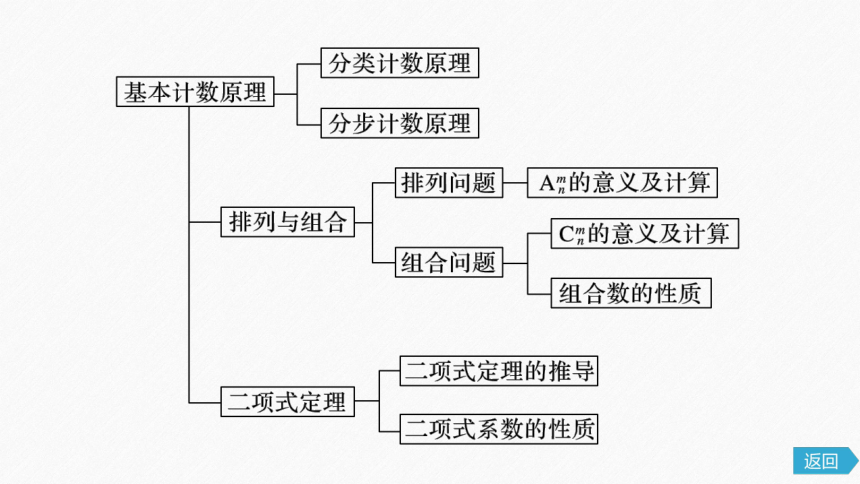
知识网络
随堂演练
知识网络
一、两个计数原理
1.分类计数原理和分步计数原理是本章内容的学习基础,在进行计数过程中,常因分类不明导致增(漏)解,因此在解题中既要保证类与类的互斥性,又要关注总数的完备性.
2.掌握两个计数原理,提升逻辑推理和数学运算素养.
例1 (1)现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这3张卡片不能是同一颜色,且绿色卡片至多1张,则不同的取法种数为
A.484 B.472 C.252 D.232
√
(2)车间有11名工人,其中5名男工是钳工,4名女工是车工,另外两名老师傅既能当车工又能当钳工,现在要在这11名工人里选派4名钳工,4名车工修理一台机床,则有多少种选派方法?
解 方法一 设A,B代表2位老师傅.
所以共有75+100+10=185(种)选派方法.
所以共有35+120+30=185(种)选派方法.
反思感悟 应用两个计数原理计数的四个步骤
(1)明确完成的这件事是什么.
(2)思考如何完成这件事.
(3)判断它属于分类还是分步,是先分类后分步,还是先分步后分类.
(4)选择计数原理进行计算.
跟踪训练1 (1)从1,2,3,4,5,6这6个数字中,任取3个数字组成无重复数字的三位数,其中,若有1和3时,3必须排在1的前面;若只有1和3中的一个时,它应排在其他数字的前面,这样不同的三位数共有____个.(用数字作答)
60
解析 1与3是特殊元素,以此为分类标准进行分类.
(2)由甲、乙、丙、丁4名学生参加数学、写作、英语三科竞赛,每科至少1人(且每人仅报一科),若学生甲、乙不能同时参加同一竞赛,则不同的参赛方案共有____种.
30
所以不同的参赛方案共有36-6=30(种).
二、排列与组合的综合应用
1.排列、组合是两类特殊的计数求解方式,在计数原理求解中起着举足轻重的作用,解决排列与组合的综合问题要树立先选后排,特殊元素(特殊位置)优先的原则.
2.明确排列和组合的运算,重点提升数学建模及数学运算的素养.
例2 在高三(1)班元旦晚会上,有6个演唱节目,4个舞蹈节目.
(1)当4个舞蹈节目要排在一起时,有多少种不同的节目安排顺序?
根据分步计数原理,一共有5 040×24=120 960(种)安排顺序.
(2)当要求每2个舞蹈节目之间至少安排1个演唱节目时,有多少种不同的节目安排顺序?
×□×□×□×□×□×□×
根据分步计数原理,一共有720×840= 604 800(种)安排顺序.
(3)若已定好节目单,后来情况有变,需加上诗朗诵和快板2个节目,但不能改变原来节目的相对顺序,有多少种不同的节目演出顺序?
反思感悟 解决排列、组合综合问题要注意以下几点
(1)首先要分清该问题是排列问题还是组合问题.
(2)对于含有多个限制条件的复杂问题,应认真分析每个限制条件,再考虑是分类还是分步,分类时要不重不漏,分步时要步步相接.
(3)对于含有“至多”“至少”的问题,常采用间接法,此时要考虑全面,排除干净.
跟踪训练2 某局安排3位副局长带5名职员去3地调研,每地至少去1名副局长和1名职员,则不同的安排方法种数为______.
900
三、二项式定理及其应用
1.二项式定理有比较广泛的应用,可用于代数式的化简、变形、证明整除、近似计算、证明不等式等,其原理可以用于二项式相应展开式项的系数求解.
2.二项式原理所体现的是一种数学运算素养.
角度1 二项展开式的“赋值问题”
例3 (1)若(2x+ )4=a0+a1x+a2x2+a3x3+a4x4,则(a0+a2+a4)2-(a1+a3)2的值为
A.-1 B.0 C.1 D.2
√
两式相乘,得
所以(a0+a2+a4)2-(a1+a3)2=(-4+3)4=1.
(2)若(3x2-2x+1)5=a10x10+a9x9+a8x8+…+a1x+a0(x∈C),求:
①(a0+a2+a4+a6+a8+a10)2-(a1+a3+a5+a7+a9)2;
解 令x=1,得a0+a1+…+a10=25;
令x=-1,得(a0+a2+a4+a6+a8+a10)-(a1+a3+a5+a7+a9)=65.
两式相乘,得(a0+a2+a4+a6+a8+a10)2-(a1+a3+a5+a7+a9)2=25×65=125.
②-a2+a4-a6+a8-a10.
解 令x=i,得-a10+a9·i+a8-a7·i-a6+a5·i+a4-a3·i-a2+a1·i+a0=(-2-2i)5=-25(1+i)5=-25[(1+i)2]2(1+i)=128+128i.
整理得(-a10+a8-a6+a4-a2+a0)+(a9-a7+a5-a3+a1)·i=128+128i,
故-a10+a8-a6+a4-a2+a0=128.
因为a0=1,所以-a10+a8-a6+a4-a2=127.
反思感悟 “赋值法”在二项展开式中的应用
(1)观察:先观察二项展开式左右两边式子的结构特征.
(2)赋值:结合待求和上述特征,对变量x赋值,常见的赋值有x=-1,x=0,x=1等,视具体情况而定.
(3)解方程:赋值后结合待求建立方程(组),求解便可.
跟踪训练3 若(x2+1)(x-3)9=a0+a1(x-2)+a2(x-2)2+a3(x-2)3+…+a11(x-2)11,则a1+a2+a3+…+a11的值为____.
5
解析 令x=2,得a0=(22+1)(2-3)9=-5,
令x=3,得a0+a1+a2+a3+…+a11=(32+1)(3-3)9=0,
所以a1+a2+a3+…+a11=-a0=5.
角度2 二项展开式的特定项问题
(1)求展开式中的所有有理项;
解得n=10(负值舍去),
于是有理项为T1=x5和T7=13 440.
(2)求展开式中系数的绝对值最大的项;
又因为r∈N,所以r=7,
解 设第r+1项系数的绝对值最大,则
当r=7时,T8=-15 360 ,
又因为当r=0时,T1=x5,
当r=10时,T11=
所以系数的绝对值最大的项为T8=-15 360 .
解 二项式系数之和为2n=256,可得n=8.
解 设常数项为第r+1项,
故8-2r=0,即r=4,
(3)若(x+m)n展开式中系数最大项只有第6项和第7项,求m的取值情况.
解 易知m>0,设第r+1项系数最大.
由于只有第6项和第7项系数最大,
所以m只能等于2.
反思感悟 二项式特定项的求解策略
(1)确定二项式中的有关元素:一般是根据已知条件,列出等式,从而可解得所要求的二项式中的有关元素.
(2)确定二项展开式中的常数项:先写出其通项公式,令未知数的指数为零,从而确定项数,然后代入通项公式,即可确定常数项.
(3)求二项展开式中条件项的系数:先写出其通项公式,再由条件确定项数,然后代入通项公式求出此项的系数.
(4)确定二项展开式中的系数最大项或最小项:利用二项式系数的性质.
解 由题意得,2n=1 024,∴n=10,
∴展开式的通项为
(2)求(1-x)3+(1-x)4+…+(1-x)n的展开式中x2项的系数.
1.知识清单:
(1)两个计数原理.
(2)排列与组合的综合应用.
(3)二项式定理及其应用.
2.方法归纳:分类讨论、先选后排法、特殊元素优先安置法、捆绑法、插空法、赋值法等.
3.常见误区:一是对于含至多、至少的问题思考不全面;二是特殊元素(位置)考虑不周;三是混淆二项式系数和项的系数.
课堂小结
随堂演练
1.在x(1+x)6的展开式中,含x3项的系数为
A.30 B.20 C.15 D.10
1
2
3
4
√
√
解析 令x=-1,得
(2+1)5=a0-a1+a2-a3+a4-a5=35,
令x=1,得(2-1)5=a0+a1+a2+a3+a4+a5=1,
∴a1+a3+a5=-121,a0+a2+a4=122,
1
2
3
4
1
2
3
4
3.身穿红、黄两种颜色衣服的各有两人,身穿蓝色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法种数共有
A.24种 B.28种 C.36种 D.48种
√
解析 分类计数原理,按红红之间有蓝无蓝两类来分.
因此,这五个人排成一行,穿相同颜色衣服的人不能相邻,则有48种排法.
1
2
3
4
4.从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成______个没有重复数字的四位数.(用数字作答)
1 260
综上,四位数的个数为720+540=1 260.
本课结束
章末复习课
第7章 计数原理
一、两个计数原理
二、排列与组合的综合应用
三、二项式定理及其应用
内容索引
知识网络
随堂演练
知识网络
一、两个计数原理
1.分类计数原理和分步计数原理是本章内容的学习基础,在进行计数过程中,常因分类不明导致增(漏)解,因此在解题中既要保证类与类的互斥性,又要关注总数的完备性.
2.掌握两个计数原理,提升逻辑推理和数学运算素养.
例1 (1)现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这3张卡片不能是同一颜色,且绿色卡片至多1张,则不同的取法种数为
A.484 B.472 C.252 D.232
√
(2)车间有11名工人,其中5名男工是钳工,4名女工是车工,另外两名老师傅既能当车工又能当钳工,现在要在这11名工人里选派4名钳工,4名车工修理一台机床,则有多少种选派方法?
解 方法一 设A,B代表2位老师傅.
所以共有75+100+10=185(种)选派方法.
所以共有35+120+30=185(种)选派方法.
反思感悟 应用两个计数原理计数的四个步骤
(1)明确完成的这件事是什么.
(2)思考如何完成这件事.
(3)判断它属于分类还是分步,是先分类后分步,还是先分步后分类.
(4)选择计数原理进行计算.
跟踪训练1 (1)从1,2,3,4,5,6这6个数字中,任取3个数字组成无重复数字的三位数,其中,若有1和3时,3必须排在1的前面;若只有1和3中的一个时,它应排在其他数字的前面,这样不同的三位数共有____个.(用数字作答)
60
解析 1与3是特殊元素,以此为分类标准进行分类.
(2)由甲、乙、丙、丁4名学生参加数学、写作、英语三科竞赛,每科至少1人(且每人仅报一科),若学生甲、乙不能同时参加同一竞赛,则不同的参赛方案共有____种.
30
所以不同的参赛方案共有36-6=30(种).
二、排列与组合的综合应用
1.排列、组合是两类特殊的计数求解方式,在计数原理求解中起着举足轻重的作用,解决排列与组合的综合问题要树立先选后排,特殊元素(特殊位置)优先的原则.
2.明确排列和组合的运算,重点提升数学建模及数学运算的素养.
例2 在高三(1)班元旦晚会上,有6个演唱节目,4个舞蹈节目.
(1)当4个舞蹈节目要排在一起时,有多少种不同的节目安排顺序?
根据分步计数原理,一共有5 040×24=120 960(种)安排顺序.
(2)当要求每2个舞蹈节目之间至少安排1个演唱节目时,有多少种不同的节目安排顺序?
×□×□×□×□×□×□×
根据分步计数原理,一共有720×840= 604 800(种)安排顺序.
(3)若已定好节目单,后来情况有变,需加上诗朗诵和快板2个节目,但不能改变原来节目的相对顺序,有多少种不同的节目演出顺序?
反思感悟 解决排列、组合综合问题要注意以下几点
(1)首先要分清该问题是排列问题还是组合问题.
(2)对于含有多个限制条件的复杂问题,应认真分析每个限制条件,再考虑是分类还是分步,分类时要不重不漏,分步时要步步相接.
(3)对于含有“至多”“至少”的问题,常采用间接法,此时要考虑全面,排除干净.
跟踪训练2 某局安排3位副局长带5名职员去3地调研,每地至少去1名副局长和1名职员,则不同的安排方法种数为______.
900
三、二项式定理及其应用
1.二项式定理有比较广泛的应用,可用于代数式的化简、变形、证明整除、近似计算、证明不等式等,其原理可以用于二项式相应展开式项的系数求解.
2.二项式原理所体现的是一种数学运算素养.
角度1 二项展开式的“赋值问题”
例3 (1)若(2x+ )4=a0+a1x+a2x2+a3x3+a4x4,则(a0+a2+a4)2-(a1+a3)2的值为
A.-1 B.0 C.1 D.2
√
两式相乘,得
所以(a0+a2+a4)2-(a1+a3)2=(-4+3)4=1.
(2)若(3x2-2x+1)5=a10x10+a9x9+a8x8+…+a1x+a0(x∈C),求:
①(a0+a2+a4+a6+a8+a10)2-(a1+a3+a5+a7+a9)2;
解 令x=1,得a0+a1+…+a10=25;
令x=-1,得(a0+a2+a4+a6+a8+a10)-(a1+a3+a5+a7+a9)=65.
两式相乘,得(a0+a2+a4+a6+a8+a10)2-(a1+a3+a5+a7+a9)2=25×65=125.
②-a2+a4-a6+a8-a10.
解 令x=i,得-a10+a9·i+a8-a7·i-a6+a5·i+a4-a3·i-a2+a1·i+a0=(-2-2i)5=-25(1+i)5=-25[(1+i)2]2(1+i)=128+128i.
整理得(-a10+a8-a6+a4-a2+a0)+(a9-a7+a5-a3+a1)·i=128+128i,
故-a10+a8-a6+a4-a2+a0=128.
因为a0=1,所以-a10+a8-a6+a4-a2=127.
反思感悟 “赋值法”在二项展开式中的应用
(1)观察:先观察二项展开式左右两边式子的结构特征.
(2)赋值:结合待求和上述特征,对变量x赋值,常见的赋值有x=-1,x=0,x=1等,视具体情况而定.
(3)解方程:赋值后结合待求建立方程(组),求解便可.
跟踪训练3 若(x2+1)(x-3)9=a0+a1(x-2)+a2(x-2)2+a3(x-2)3+…+a11(x-2)11,则a1+a2+a3+…+a11的值为____.
5
解析 令x=2,得a0=(22+1)(2-3)9=-5,
令x=3,得a0+a1+a2+a3+…+a11=(32+1)(3-3)9=0,
所以a1+a2+a3+…+a11=-a0=5.
角度2 二项展开式的特定项问题
(1)求展开式中的所有有理项;
解得n=10(负值舍去),
于是有理项为T1=x5和T7=13 440.
(2)求展开式中系数的绝对值最大的项;
又因为r∈N,所以r=7,
解 设第r+1项系数的绝对值最大,则
当r=7时,T8=-15 360 ,
又因为当r=0时,T1=x5,
当r=10时,T11=
所以系数的绝对值最大的项为T8=-15 360 .
解 二项式系数之和为2n=256,可得n=8.
解 设常数项为第r+1项,
故8-2r=0,即r=4,
(3)若(x+m)n展开式中系数最大项只有第6项和第7项,求m的取值情况.
解 易知m>0,设第r+1项系数最大.
由于只有第6项和第7项系数最大,
所以m只能等于2.
反思感悟 二项式特定项的求解策略
(1)确定二项式中的有关元素:一般是根据已知条件,列出等式,从而可解得所要求的二项式中的有关元素.
(2)确定二项展开式中的常数项:先写出其通项公式,令未知数的指数为零,从而确定项数,然后代入通项公式,即可确定常数项.
(3)求二项展开式中条件项的系数:先写出其通项公式,再由条件确定项数,然后代入通项公式求出此项的系数.
(4)确定二项展开式中的系数最大项或最小项:利用二项式系数的性质.
解 由题意得,2n=1 024,∴n=10,
∴展开式的通项为
(2)求(1-x)3+(1-x)4+…+(1-x)n的展开式中x2项的系数.
1.知识清单:
(1)两个计数原理.
(2)排列与组合的综合应用.
(3)二项式定理及其应用.
2.方法归纳:分类讨论、先选后排法、特殊元素优先安置法、捆绑法、插空法、赋值法等.
3.常见误区:一是对于含至多、至少的问题思考不全面;二是特殊元素(位置)考虑不周;三是混淆二项式系数和项的系数.
课堂小结
随堂演练
1.在x(1+x)6的展开式中,含x3项的系数为
A.30 B.20 C.15 D.10
1
2
3
4
√
√
解析 令x=-1,得
(2+1)5=a0-a1+a2-a3+a4-a5=35,
令x=1,得(2-1)5=a0+a1+a2+a3+a4+a5=1,
∴a1+a3+a5=-121,a0+a2+a4=122,
1
2
3
4
1
2
3
4
3.身穿红、黄两种颜色衣服的各有两人,身穿蓝色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法种数共有
A.24种 B.28种 C.36种 D.48种
√
解析 分类计数原理,按红红之间有蓝无蓝两类来分.
因此,这五个人排成一行,穿相同颜色衣服的人不能相邻,则有48种排法.
1
2
3
4
4.从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成______个没有重复数字的四位数.(用数字作答)
1 260
综上,四位数的个数为720+540=1 260.
本课结束
