三角形的内角和
图片预览





文档简介
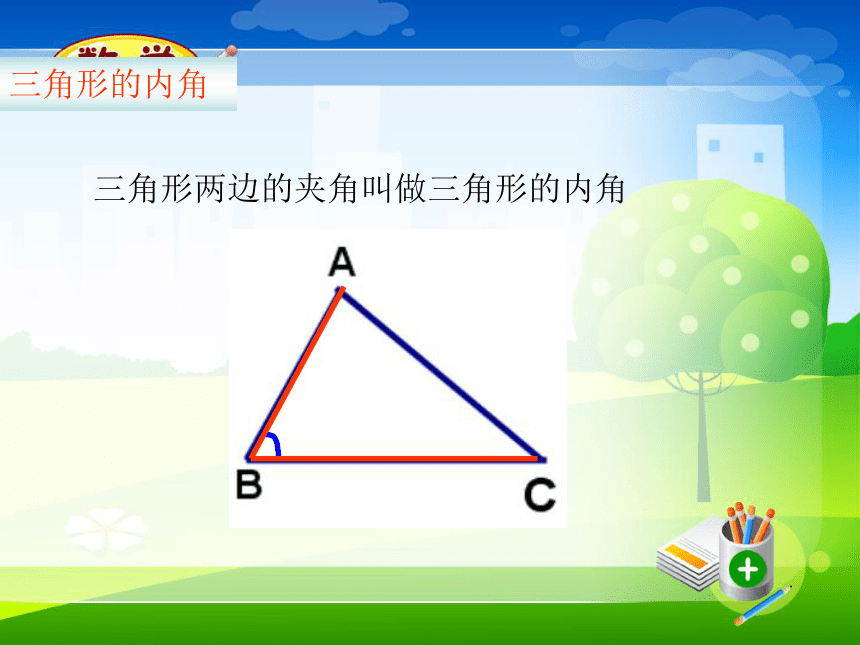
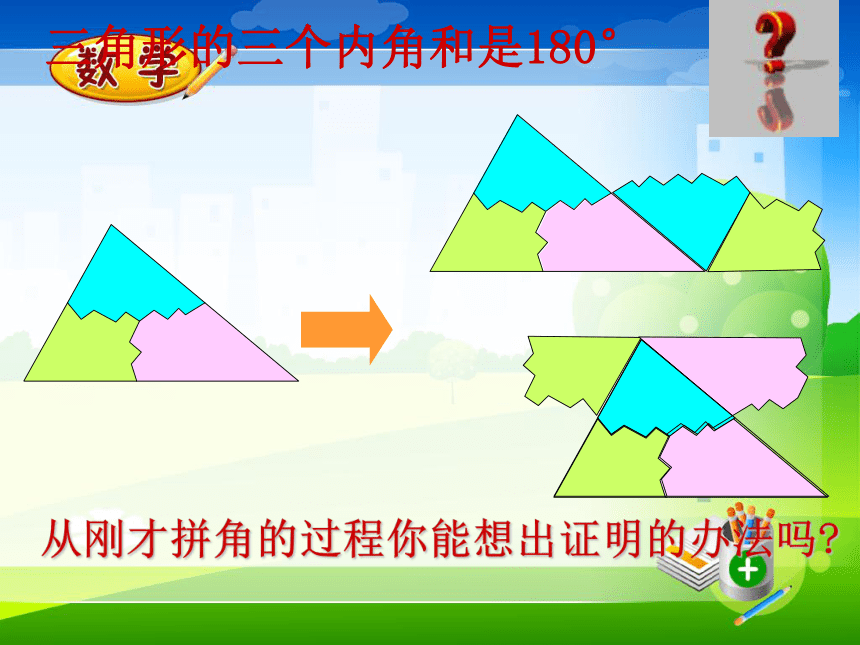
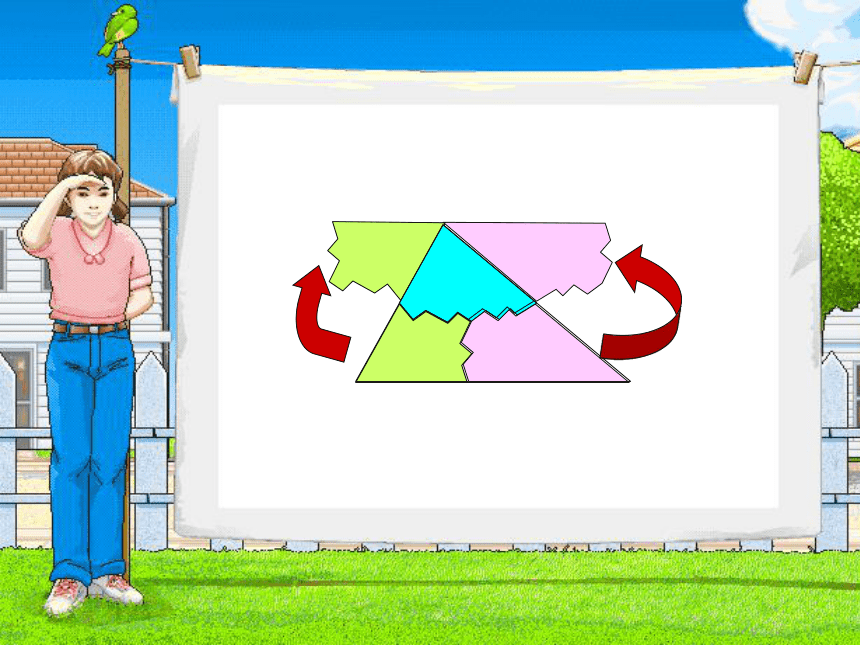
课件27张PPT。 三角形的内角7.2.1 三角形两边的夹角叫做三角形的内角三角形的内角三角形的三个内角和是多少?把三个角拼在一起试试看?你有什么办法可以验证呢?180°三角形的三个内角和是180° 从刚才拼角的过程你能想出证明的办法吗?为什么要证明 按照上面的方法,已经可以验证三角形的内角和是180°,但是由于形状不同的三角形有无数多个,我们不可能通过上面的办法一一验证.再加上其验证过程中可能存在误差,不能保证其有效性.所以我们需要一种能证明任意一个三角形的内角和等于180°的方法.这个方法就是—证明.
一个命题是否正确,需要经过使人信服的推理论证才能得出结论.而证明是由命题的题设(已知)出发,经过严密的推理,最后推出结论(求证)正确的过程. 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成------虚线。
证明一:过A作EF∥BA,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°三角形的内角和等于1800.三角形内角和定理:证明二:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°21EDCBA三角形的内角和等于1800.三角形内角和定理:证明三:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°三角形的内角和等于1800.思路总结 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= . 102 °80 °60 °40 °新知应用(1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?211讨论1 三角形中最大的角是锐角,那么这个三角 形是锐角三角形( )
2 一个三角形中最多只有一个钝角或直角( )
3 一个等腰三角形一定是锐角三角形( )
判断正误×√√ABC已知△ABC中,∠ABC=∠C=2∠A ,
BD是AC边上的高,求∠DBC的度数。解:设∠A=x0,则∠ABC=∠C=2x0∴x+2x+2x=180(三角形内角和定理)解得x=36∴∠C=2×360=720∴∠DBC=1800-900-720(三角形内角和定理)在△BDC中,∵∠BDC=900
(三角形高的定义)∴∠DBC=180?例题讲解1如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求下面各题.(1)∠DAC=_____ ∠DAB=______ ∠EBC=_______ ∠CAB = ______ A(2)从C岛看A 、B两岛的视角∠C是多少?50°80°40°北解:∵ AD∥BE
∴ ∠DAB﹢∠ABE=180° ∴ ∠ABE = 180°-∠DAB = 180° - 80° =100° 在△ABC中,∠C = 180° - ∠CAB - ∠ABC= 180°-30 °-60 °=90°∴ ∠ABC=∠ABE﹣∠CBE30 °=100°﹣40°=60°例题讲解2DCE北A50°∟B40 °北MN在△AMC中 ∠AMC=90°, ∠MAC=50°解:过点C画MN⊥AD分别交AD、BE于点M、N12例:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。∴∠1=180 °-90°-50° =40°∵ AD∥BE∴ ∠AMC+ ∠BNC =180 °∴ ∠BNC =90°同理得∠2 =50°∴ ∠ACB =180 ° -∠1 -∠2=180 °-40°-50° =90°例题讲解2B 你能想出一个更简捷的方法来求∠C的度数吗?1250°40°解: 过点C画CF∥AD ∴ ∠1=∠DAC=50 °, F∵ CF∥AD, 又AD ∥BE∴ CF∥ BE∴∠2=∠CBE =40 °∴ ∠ACB=∠1﹢∠2 =50 °﹢ 40 ° =90 °例题讲解2解:在△ACD中 ∠CAD =30 ° ∠D =90 °∴ ∠ACD =180 ° -30 ° -90 °=6 0 °在△BCD中 ∠CBD = 45 ° ∠D =90 ° ∴ ∠BCD = 180 °- 90°-45 °=45 °∴ ∠ACB = ∠ACD - ∠BCD = 6 0 °- 45 °巩固练习1.如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少?2、已知三角形三个内角的度数之比为
1:3:5,求这三个内角的度数。 解:设三个内角度数分别为:x、3x、5x,
由三角形内角和为180°得3. 如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°, 求∠BDC的度数.解:∵∠A=70° ∴∠ACB=180 °-∠A-∠B=180°-70°-50°=60°∵DE//BC∴∠B=∠ADE=50°∵ CD平分∠ACB巩固练习 在△ABC中,如果∠A= ∠B= ∠ C,那么△ABC是什么三角形?解:设∠A=x°,那么∠B=2x°,∠C=3x°根据题意得:拓展与思考解得∴∠A=30°,∠B=60°,∠C=90°所以△ABC是直角三角形这节课你有那些收获?1、三角形的内角和:三角形三个内角之和为180°2、由三角形内角和等于180°,可得出(1)、直角三角形两锐角互余;(2)、一个三角形最多有一个直角或钝角;(3)、任意一个三角形中,最多有三个锐角,最少有两个锐角;(4)、一个三角形中至少有一个角小于或等于60°3、三角形按角分类:三角形直角三角形斜三角形锐角三角形钝角三角形小结作业:教科书76页习题7.2第3、4题Thanks!
一个命题是否正确,需要经过使人信服的推理论证才能得出结论.而证明是由命题的题设(已知)出发,经过严密的推理,最后推出结论(求证)正确的过程. 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成------虚线。
证明一:过A作EF∥BA,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°三角形的内角和等于1800.三角形内角和定理:证明二:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°21EDCBA三角形的内角和等于1800.三角形内角和定理:证明三:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°三角形的内角和等于1800.思路总结 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= . 102 °80 °60 °40 °新知应用(1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?211讨论1 三角形中最大的角是锐角,那么这个三角 形是锐角三角形( )
2 一个三角形中最多只有一个钝角或直角( )
3 一个等腰三角形一定是锐角三角形( )
判断正误×√√ABC已知△ABC中,∠ABC=∠C=2∠A ,
BD是AC边上的高,求∠DBC的度数。解:设∠A=x0,则∠ABC=∠C=2x0∴x+2x+2x=180(三角形内角和定理)解得x=36∴∠C=2×360=720∴∠DBC=1800-900-720(三角形内角和定理)在△BDC中,∵∠BDC=900
(三角形高的定义)∴∠DBC=180?例题讲解1如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求下面各题.(1)∠DAC=_____ ∠DAB=______ ∠EBC=_______ ∠CAB = ______ A(2)从C岛看A 、B两岛的视角∠C是多少?50°80°40°北解:∵ AD∥BE
∴ ∠DAB﹢∠ABE=180° ∴ ∠ABE = 180°-∠DAB = 180° - 80° =100° 在△ABC中,∠C = 180° - ∠CAB - ∠ABC= 180°-30 °-60 °=90°∴ ∠ABC=∠ABE﹣∠CBE30 °=100°﹣40°=60°例题讲解2DCE北A50°∟B40 °北MN在△AMC中 ∠AMC=90°, ∠MAC=50°解:过点C画MN⊥AD分别交AD、BE于点M、N12例:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。∴∠1=180 °-90°-50° =40°∵ AD∥BE∴ ∠AMC+ ∠BNC =180 °∴ ∠BNC =90°同理得∠2 =50°∴ ∠ACB =180 ° -∠1 -∠2=180 °-40°-50° =90°例题讲解2B 你能想出一个更简捷的方法来求∠C的度数吗?1250°40°解: 过点C画CF∥AD ∴ ∠1=∠DAC=50 °, F∵ CF∥AD, 又AD ∥BE∴ CF∥ BE∴∠2=∠CBE =40 °∴ ∠ACB=∠1﹢∠2 =50 °﹢ 40 ° =90 °例题讲解2解:在△ACD中 ∠CAD =30 ° ∠D =90 °∴ ∠ACD =180 ° -30 ° -90 °=6 0 °在△BCD中 ∠CBD = 45 ° ∠D =90 ° ∴ ∠BCD = 180 °- 90°-45 °=45 °∴ ∠ACB = ∠ACD - ∠BCD = 6 0 °- 45 °巩固练习1.如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少?2、已知三角形三个内角的度数之比为
1:3:5,求这三个内角的度数。 解:设三个内角度数分别为:x、3x、5x,
由三角形内角和为180°得3. 如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°, 求∠BDC的度数.解:∵∠A=70° ∴∠ACB=180 °-∠A-∠B=180°-70°-50°=60°∵DE//BC∴∠B=∠ADE=50°∵ CD平分∠ACB巩固练习 在△ABC中,如果∠A= ∠B= ∠ C,那么△ABC是什么三角形?解:设∠A=x°,那么∠B=2x°,∠C=3x°根据题意得:拓展与思考解得∴∠A=30°,∠B=60°,∠C=90°所以△ABC是直角三角形这节课你有那些收获?1、三角形的内角和:三角形三个内角之和为180°2、由三角形内角和等于180°,可得出(1)、直角三角形两锐角互余;(2)、一个三角形最多有一个直角或钝角;(3)、任意一个三角形中,最多有三个锐角,最少有两个锐角;(4)、一个三角形中至少有一个角小于或等于60°3、三角形按角分类:三角形直角三角形斜三角形锐角三角形钝角三角形小结作业:教科书76页习题7.2第3、4题Thanks!
