用列举法求概率
图片预览





文档简介
课件19张PPT。用列举法求概率 一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含在其中的m种结果,那么事件A发生的概率为:求概率的步骤:(1)列举出一次试验中的所有结果(n个);(2)找出其中事件A发生的结果(m个);(3)运用公式求事件A的概率:知识回顾 小佳在游戏开始时,踩中后
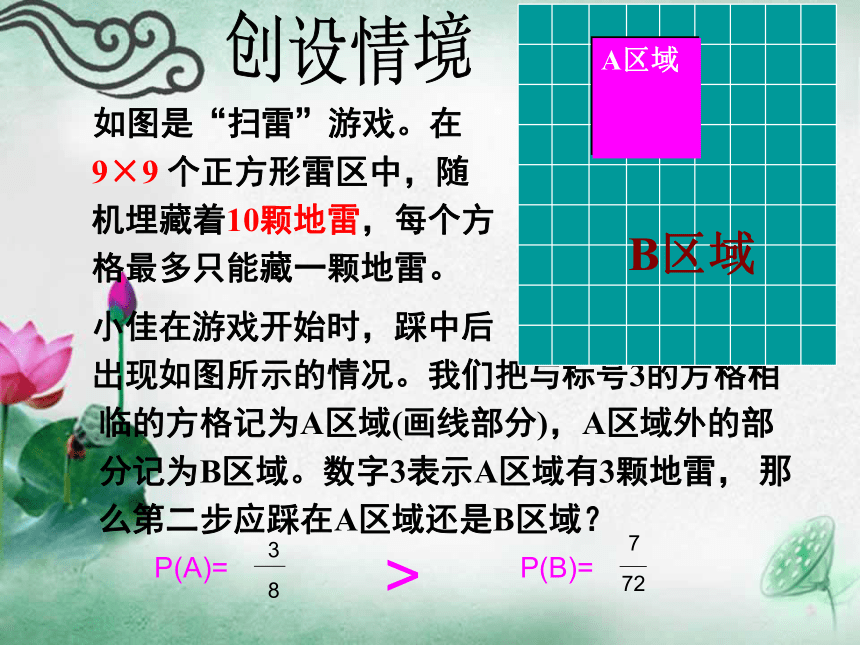
出现如图所示的情况。我们把与标号3的方格相临的方格记为A区域(画线部分),A区域外的部分记为B区域。数字3表示A区域有3颗地雷, 那么第二步应踩在A区域还是B区域?A区域
如图是“扫雷”游戏。在9×9 个正方形雷区中,随机埋藏着10颗地雷,每个方格最多只能藏一颗地雷。B区域创设情境P(A)=P(B)=>掷两枚硬币,求下列事件的概率:
(1)两枚硬币全部正面朝上;
(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上;“掷两枚硬币”共有几种结果?正正正反反正反反引例 同时掷两个质地相同的骰子,计算下列事件的概率:
(1)两个骰子的点数相同;
(2)两个骰子的点数和是9;
(3)至少有个骰子的点数是2。问题为了不重不漏地列出所有这些结果,
你有什么好办法吗?
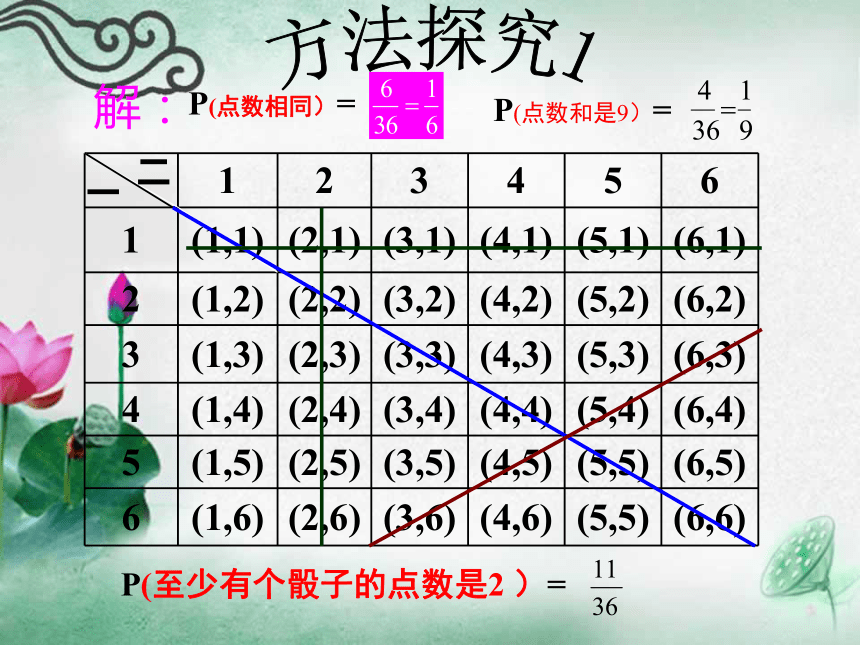
解:二一P(点数相同)=P(点数和是9)=P(至少有个骰子的点数是2 )=方法探究1“列表法”的意义: 当试验涉及两个因素(例如两个转盘,两个骰子)
并且可能出现的结果数目较多时,
为不重不漏地列出所有的结果,
通常采用“列表法”。知识归纳 “同时掷两个质地相同的骰子”与
“把一个骰子掷两次”,所得到的结果有变化吗?“同时掷两个质地相同的骰子”两个骰子各出现的点数为1~6点“把一个骰子掷两次”两次骰子各出现的点数仍为1~6点归纳 “两个相同的随机事件同时发生”与
“一个随机事件先后两次发生”的结果是一样的。随机事件“同时”与“先后”的关系:思考一 如图,甲转盘的三个等分区域分别写有数字1、2、3,乙转盘的四个等分区域分别写有数字4、5、6、7。现分别转动两个转盘,求指针所指数字之和为偶数的概率。解:甲(1,4)(1,5)(1,6)(1,7)(2,4)(2,5)(2,6)(2,7)(3,4)(3,5)(3,6)(3,7)乙共有12种不同结果,每种结果出现的可能性相同,其中数字和为偶数的有 6 种∴P(数字和为偶数)
=例题一同时抛掷三枚硬币,求下列事件的概率:
(1) 三枚硬币全部正面朝上;
(2) 至少有两枚硬币正面朝上.问题二 方法探究2抛掷硬币试验正反正反正反正反正反正反正反第①枚②③解: 由树形图可以看出,抛掷3枚硬币的结果有8种,它们出现的可能性相等.∴ P(A)(1)满足三枚硬币全部正面朝上(记为事件A)的结果只有1种。(2)满足至少有两枚硬币正面朝上(记为事件C)的结果有4种。∴ P(C)用树状图和列表的方法求概率的前提:
1·实验结果有有限多个
2·各种结果出现的可能性务必相同.
当实验涉及3个或3个以上因素时
常采用树形图法
注意:知识归纳一个袋子中装有3个红球和1个绿球1个黄球,任意摸出一个球,记录颜色后放回,连续摸3次,请你计算3次都摸到红球的概率。若第一次摸出一球后,不放回,结果又会怎样?“放回”与“不放回”的区别:(1)“放回”可以看作两次相同的试验;(2)“不放回”则看作两次不同的试验。思考二甲、乙、丙三人打乒乓球.由哪两人先打呢?他们决定用 “石头、剪刀、布”的游戏来决定,游戏时三人每次做“石头” “剪刀”“布”三种手势中的一种,规定“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”. 问一次比赛能淘汰一人的概率是多少?解: 由树形图可以看出,游戏的结果有27种,它们出现的可能性相等. 由规则可知,一次能淘汰一人的结果应是:“石石剪” “剪剪布” “布布石”三类.而满足条件(记为事件A)的结果有9种∴ P(A)=例题二1.小明和小丽都想去看电影,但只有一张电影票.小明提议:利用这三张牌,洗匀后任意抽一张,放回,再洗匀抽一张牌.连续抽的两张牌结果为一张5一张4小明去,抽到两张5的小丽去,两张4重新抽.小明的
办法对双方公平吗?
课堂巩固练习2. 用数字1、2、3,组成三位数,求其中恰有2个相同的数字的概率.解: 由树形图可以看出,所有可能的结果有27种,它们出现的可能性相等.其中恰有2个数字相同的结果有18个.∴ P(恰有两个数字相同)=课堂巩固练习(1) 列表法和树形图法的优点是什么?
(2)什么时候使用“列表法”方便?什么时候使用“树 形图法”方便? 利用树形图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.
当试验包含两步时,列表法比较方便,当然,此时也可以用树形图法;
当试验在三步或三步以上时,用树形图法方便.方法对比奥地利遗传学家孟德尔曾经将纯种的黄豌豆和绿豆杂交,得到杂种第一代豌豆,再用杂种第一代豌豆自交,产生杂交第二代豌豆,孟德尔发现第一代豌豆全是黄的,第二代豌豆有黄的,也有绿的,但黄色和绿色的比是一个常数。孟德尔经过分析以后,可以用遗传学理论解释这个现象,比如设纯种黄豌豆的基因是yy,纯种绿豌豆的基因是gg,黄色基因是显性的,接下来,你可以替孟德尔来解释吗?第二代豌豆是绿豌豆的概率是多少呢?想一想,生活中还有类似现象吗?你能设法解释这一现象吗?拓展延伸列举发求概率的方法
随机事件中同时与先后的关系
随机事件中放回与不放回的区别
灵活选择恰当方法求事件概率
课堂小结
出现如图所示的情况。我们把与标号3的方格相临的方格记为A区域(画线部分),A区域外的部分记为B区域。数字3表示A区域有3颗地雷, 那么第二步应踩在A区域还是B区域?A区域
如图是“扫雷”游戏。在9×9 个正方形雷区中,随机埋藏着10颗地雷,每个方格最多只能藏一颗地雷。B区域创设情境P(A)=P(B)=>掷两枚硬币,求下列事件的概率:
(1)两枚硬币全部正面朝上;
(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上;“掷两枚硬币”共有几种结果?正正正反反正反反引例 同时掷两个质地相同的骰子,计算下列事件的概率:
(1)两个骰子的点数相同;
(2)两个骰子的点数和是9;
(3)至少有个骰子的点数是2。问题为了不重不漏地列出所有这些结果,
你有什么好办法吗?
解:二一P(点数相同)=P(点数和是9)=P(至少有个骰子的点数是2 )=方法探究1“列表法”的意义: 当试验涉及两个因素(例如两个转盘,两个骰子)
并且可能出现的结果数目较多时,
为不重不漏地列出所有的结果,
通常采用“列表法”。知识归纳 “同时掷两个质地相同的骰子”与
“把一个骰子掷两次”,所得到的结果有变化吗?“同时掷两个质地相同的骰子”两个骰子各出现的点数为1~6点“把一个骰子掷两次”两次骰子各出现的点数仍为1~6点归纳 “两个相同的随机事件同时发生”与
“一个随机事件先后两次发生”的结果是一样的。随机事件“同时”与“先后”的关系:思考一 如图,甲转盘的三个等分区域分别写有数字1、2、3,乙转盘的四个等分区域分别写有数字4、5、6、7。现分别转动两个转盘,求指针所指数字之和为偶数的概率。解:甲(1,4)(1,5)(1,6)(1,7)(2,4)(2,5)(2,6)(2,7)(3,4)(3,5)(3,6)(3,7)乙共有12种不同结果,每种结果出现的可能性相同,其中数字和为偶数的有 6 种∴P(数字和为偶数)
=例题一同时抛掷三枚硬币,求下列事件的概率:
(1) 三枚硬币全部正面朝上;
(2) 至少有两枚硬币正面朝上.问题二 方法探究2抛掷硬币试验正反正反正反正反正反正反正反第①枚②③解: 由树形图可以看出,抛掷3枚硬币的结果有8种,它们出现的可能性相等.∴ P(A)(1)满足三枚硬币全部正面朝上(记为事件A)的结果只有1种。(2)满足至少有两枚硬币正面朝上(记为事件C)的结果有4种。∴ P(C)用树状图和列表的方法求概率的前提:
1·实验结果有有限多个
2·各种结果出现的可能性务必相同.
当实验涉及3个或3个以上因素时
常采用树形图法
注意:知识归纳一个袋子中装有3个红球和1个绿球1个黄球,任意摸出一个球,记录颜色后放回,连续摸3次,请你计算3次都摸到红球的概率。若第一次摸出一球后,不放回,结果又会怎样?“放回”与“不放回”的区别:(1)“放回”可以看作两次相同的试验;(2)“不放回”则看作两次不同的试验。思考二甲、乙、丙三人打乒乓球.由哪两人先打呢?他们决定用 “石头、剪刀、布”的游戏来决定,游戏时三人每次做“石头” “剪刀”“布”三种手势中的一种,规定“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”. 问一次比赛能淘汰一人的概率是多少?解: 由树形图可以看出,游戏的结果有27种,它们出现的可能性相等. 由规则可知,一次能淘汰一人的结果应是:“石石剪” “剪剪布” “布布石”三类.而满足条件(记为事件A)的结果有9种∴ P(A)=例题二1.小明和小丽都想去看电影,但只有一张电影票.小明提议:利用这三张牌,洗匀后任意抽一张,放回,再洗匀抽一张牌.连续抽的两张牌结果为一张5一张4小明去,抽到两张5的小丽去,两张4重新抽.小明的
办法对双方公平吗?
课堂巩固练习2. 用数字1、2、3,组成三位数,求其中恰有2个相同的数字的概率.解: 由树形图可以看出,所有可能的结果有27种,它们出现的可能性相等.其中恰有2个数字相同的结果有18个.∴ P(恰有两个数字相同)=课堂巩固练习(1) 列表法和树形图法的优点是什么?
(2)什么时候使用“列表法”方便?什么时候使用“树 形图法”方便? 利用树形图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.
当试验包含两步时,列表法比较方便,当然,此时也可以用树形图法;
当试验在三步或三步以上时,用树形图法方便.方法对比奥地利遗传学家孟德尔曾经将纯种的黄豌豆和绿豆杂交,得到杂种第一代豌豆,再用杂种第一代豌豆自交,产生杂交第二代豌豆,孟德尔发现第一代豌豆全是黄的,第二代豌豆有黄的,也有绿的,但黄色和绿色的比是一个常数。孟德尔经过分析以后,可以用遗传学理论解释这个现象,比如设纯种黄豌豆的基因是yy,纯种绿豌豆的基因是gg,黄色基因是显性的,接下来,你可以替孟德尔来解释吗?第二代豌豆是绿豌豆的概率是多少呢?想一想,生活中还有类似现象吗?你能设法解释这一现象吗?拓展延伸列举发求概率的方法
随机事件中同时与先后的关系
随机事件中放回与不放回的区别
灵活选择恰当方法求事件概率
课堂小结
同课章节目录
