用列举法求概率(2)

课件30张PPT。25.2. 用列举法求概率（2）燕矶中学九年级数学备课组复习引入 等可能性事件（古典概率）的两个特征：
1.出现的结果有限多个;
2.各结果发生的可能性相等；求等可能性事件的概率-----列举法 一个口袋内装有大小相等的1个红球和已编有不同号码的3个黑球，一次从中摸出2个球.
（1）共有多少种不同的结果？
（2）摸出2个黑球有多种不同的结果？
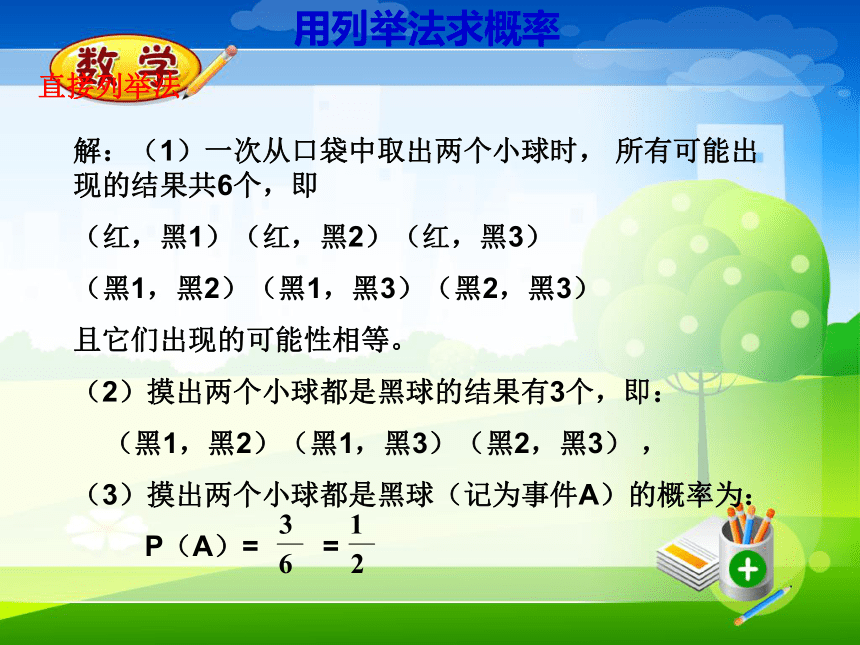
（3）摸出两个黑球的概率是多少？想一想:直接列举法用列举法求概率解：（1）一次从口袋中取出两个小球时， 所有可能出现的结果共6个，即
（红，黑1）（红，黑2）（红，黑3）
（黑1，黑2）（黑1，黑3）（黑2，黑3）
且它们出现的可能性相等。
（2）摸出两个小球都是黑球的结果有3个，即：
（黑1，黑2）（黑1，黑3）（黑2，黑3） ，
（3）摸出两个小球都是黑球（记为事件A）的概率为：
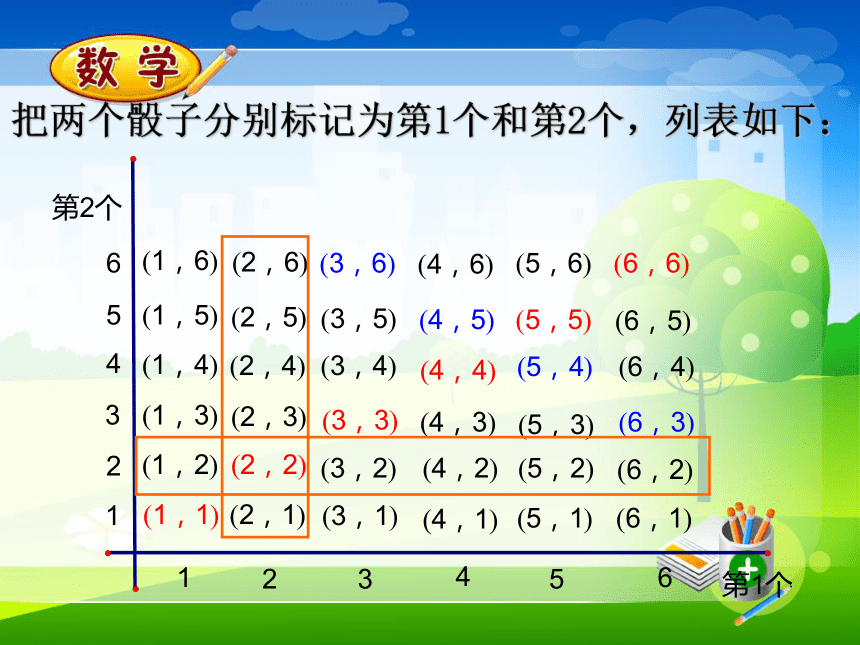
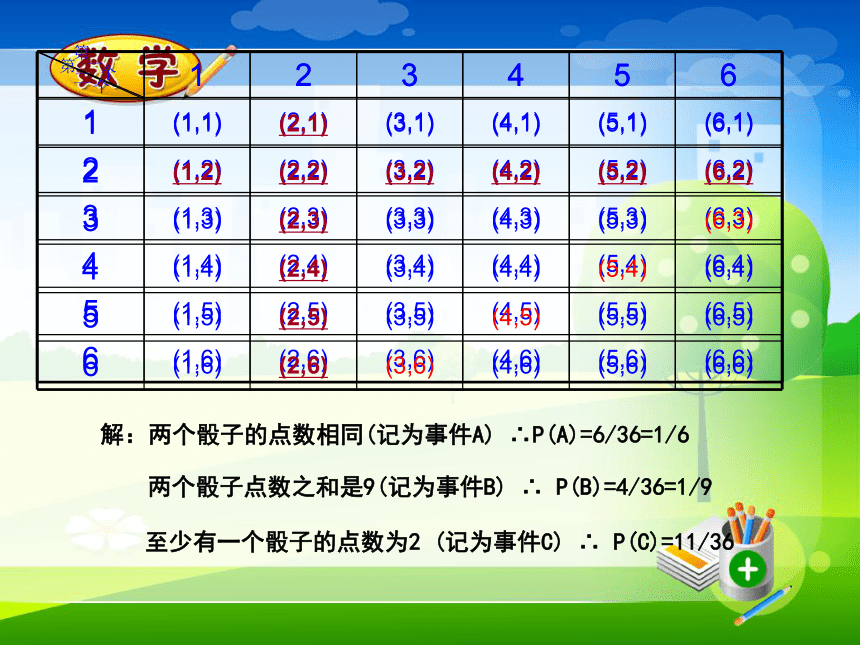
P（A）= =直接列举法问题：利用直接列举法可以看出事件发生的各种情况，对于列举复杂事件的发生情况还有什么更好的方法呢？例.同时掷两个质地均匀的骰子，计算下列事件的概率：（1）两个骰子的点数相同;（2）两个骰子点数的和是9；（3）至少有一个骰子的点数为2。 当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.两个因素所组合的所有可能情况,即n 在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.一个因素所包含的可能情况 另一个因素所包含的可能情况列表法中表格构造特点:把两个骰子分别标记为第1个和第2个，列表如下：解：由表可看出，同时投掷两个骰子，可能
出现的结果有36个，它们出现的可能性相等。（1）满足两个骰子点数相同（记为事件A）的结果有6个（2）满足两个骰子点数和为9（记为事件B）的结果有4个（3）满足至少有一个骰子的点数为2（记为事件C）的结果有11个。解：两个骰子的点数相同(记为事件A) ∴P(A)=6/36=1/6两个骰子点数之和是9(记为事件B) ∴ P(B)=4/36=1/9至少有一个骰子的点数为2 (记为事件C) ∴ P(C)=11/36想一想: 如果把例题中的“同时掷两个骰子”改为
“把一个骰子掷两次”,所得的结果有变化
吗?没有变化 口袋中一红三黑共4个小球，
⑴第一次从中取出一个小球后放回，第二次再取一个小球,求 “两次取出的小球都是黑球”的概率.
⑵一次取出两个小球,求“两个小球都是黑球”的概率。用列举法求概率试一试这个游戏对小亮和小明公平吗？
小明和小亮做扑克游戏，桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时，你得1分，为偶数我得1分,先得到10分的获胜”。如果你是小亮,你愿意接受这个游戏的规则吗? 思考:你能求出小亮得分的概率吗?用列表法求解总结经验:
当一次试验要涉及两个因素,并且可能出
现的结果数目较多时,为了不重不漏的列
出所有可能的结果,通常采用列表的办法解:由表中可以看出,在两堆牌中分别取一张,它可
能出现的结果有36个,它们出现的可能性相等
满足两张牌的数字之积为奇数(记为事件A)
的有(1,1)(1,3)(1,5)(3,1)(3,3)(3,5)(5,1)(5,3)(5,5)
这9种情况,所以

P(A)=
随堂练习
（基础练习）1、一个袋子中装有2个红球和2个绿球,任意摸出一球,记录颜色放回,再任意摸出一球,记录颜色放回,请你估计两次都摸到红球的概率是________。2、某人有红、白、蓝三件衬衫和红、白、蓝三条长裤，该人任意拿一件衬衫和一条长裤，求正好是一套白色的概率_________。3、在6张卡片上分别写有1—6的整数,随机的抽取一张后放回,再随机的抽取一张，那么,第一次取出的数字能够整除第2次取出的数字的概率是多少?解：将两次抽取卡片记为第1个和第2个，用表格列出所有可能出现的情况，如图所示，共有36种情况。 则将第1个数字能整除第2个数字事件记为事件A，满足情况的有（1，1），（2，1），（2，2），（3，1），（3，3），（4，1），（4，2），
（4，4），（5，1），（5，5），（6，1）（6，2），（6，3），（6，6）。 要“玩”出水平“配紫色”游戏4、小颖为联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.(1)利用列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少?
真知灼见源于实践表格可以是：“配紫色”游戏游戏者获胜的概率是1/6.黄蓝绿红(红,黄)(红,蓝)(红,绿)白(白,黄)(白,蓝)(白,绿)行家看“门道” 5、如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.用心领“悟”解:每次游戏时,所有可能出现的结果如下:游戏者获胜的概率为1/6.112(1,1)(1,2)2(2,1)(2,2)3(1,3)(2,3)1、现有两组电灯，每一组中各有红、黄、蓝、绿四盏灯，各组中的灯均为并联，两组灯同时只能各亮一盏，求同时亮红灯的概率。拓展升华将所有可能出现的情况列表如下： 2、染色体隐性遗传病，只有致病基因在纯合状态（dd）时才会发病，在杂合状态（Dd）时，由于正常的显性基因型D存在，致病基因d的作用不能表现出来，但是自己虽不发病，却能将病传给后代，常常父母无病，子女有病，如下表所示：（1）子女发病的概率是多少？
（2）如果父亲基因型为Dd，母亲基因型为dd，问子女发病的概率是多少？利用列表法可以清晰地表示出某个事件发生的所有可能出现的结果;
从而较方便地求出某些事件发生的概率.
对于今天学习列举法求概率时应注意什么？课时小结 用列表法求出所有可能的结果时，要注意表格的设计，做到使各种可能结果既不重复也不遗漏 。课时作业：1、从-1，1，2这三个数中，任取两个不同的数作为一次函数y=kx+b的系数k，b，则一次函数y=kx+b的图象不经过第四象限的概率是 。
你喜欢玩游戏吗现请你玩一个转盘游戏．如图所示的两个转盘中指针落在每一个数字上的机会均等，现同时自由转动甲乙两个转盘，转盘停止后，指针各指向一个数字，用所指的两个数字作乘积．请你：
（1）用列表列举所有可能得到的数字之积；
（2）求出数字之积为奇数的概率．3、如图．电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A，B，C都可使小灯泡发光．（1）任意闭合其中一个开关，则小灯泡发光的概率等于
?（2）任意闭合其中两个开关，请用列表的方法求出小灯泡发光的概率．4、如图所示，两个转盘均被分成三等份，甲、乙二人利用它们做游戏，同时自由转动两个转盘，如果指针所停区域的颜色相同，则甲胜；如果指针所停区域的颜色不相同，则乙获胜．试计算：甲、乙二人获胜的概率各是多少？这个游戏对甲、乙双方公平吗？5、有两个可以自由转动的均匀转盘A、B，都被分成了3等份，并在每份内均标有数字，如图所示，规则如下：①分别转动转盘A、B．②两个转盘停止后，将两个指针所指份内的数字相乘（若指针停在等分线上，那么重转一次，直到指针指向某一份为止）．（1）用列表法分别求出数字之积为3的倍数和为5的倍数的概率；（2）小亮和小芸想用这两个转盘做游戏，他们规定：数字之积为3的倍数时，小亮得2分；数字之积为5的倍数时，小芸得3分．这个游戏对双方公平吗？请说明理由；认为不公平的，试修改得分规定，使游戏双方公平．6、两人要去某风景区游玩，每天某一时段开往该风景区有三辆汽车（票价相同），但是他们不知道这些车的舒适程度，也不知道汽车开过来的顺序．两人采用了不同的乘车方案：甲无论如何总是上开来的第一辆车．而乙则是先观察后上车，当第一辆车开来时，他不上车，而是仔细观察车的舒适状况．如果第二辆车的状况比第一辆好，他就上第二辆车；如果第二辆不比第一辆好，他就上第三辆车．如果把这三辆车的舒适程度分为上、中、下三等，请尝试着解决下面的问题：（1）三辆车按出现的先后顺序共有哪几种不同的可能？（2）你认为甲、乙两人采用的方案，哪一种方案使自己乘坐上等车的可能性大，为什么？再见