2021-2022学年度北师大版七年级数学下册:2.3 平行线的性质 同步练习(word版,含答案)
文档属性
| 名称 | 2021-2022学年度北师大版七年级数学下册:2.3 平行线的性质 同步练习(word版,含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 103.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 00:00:00 | ||
图片预览

文档简介
2021-2022学年度北师大版七年级数学下册
2.3 平行线的性质 同步练习(含答案)
一、单选题
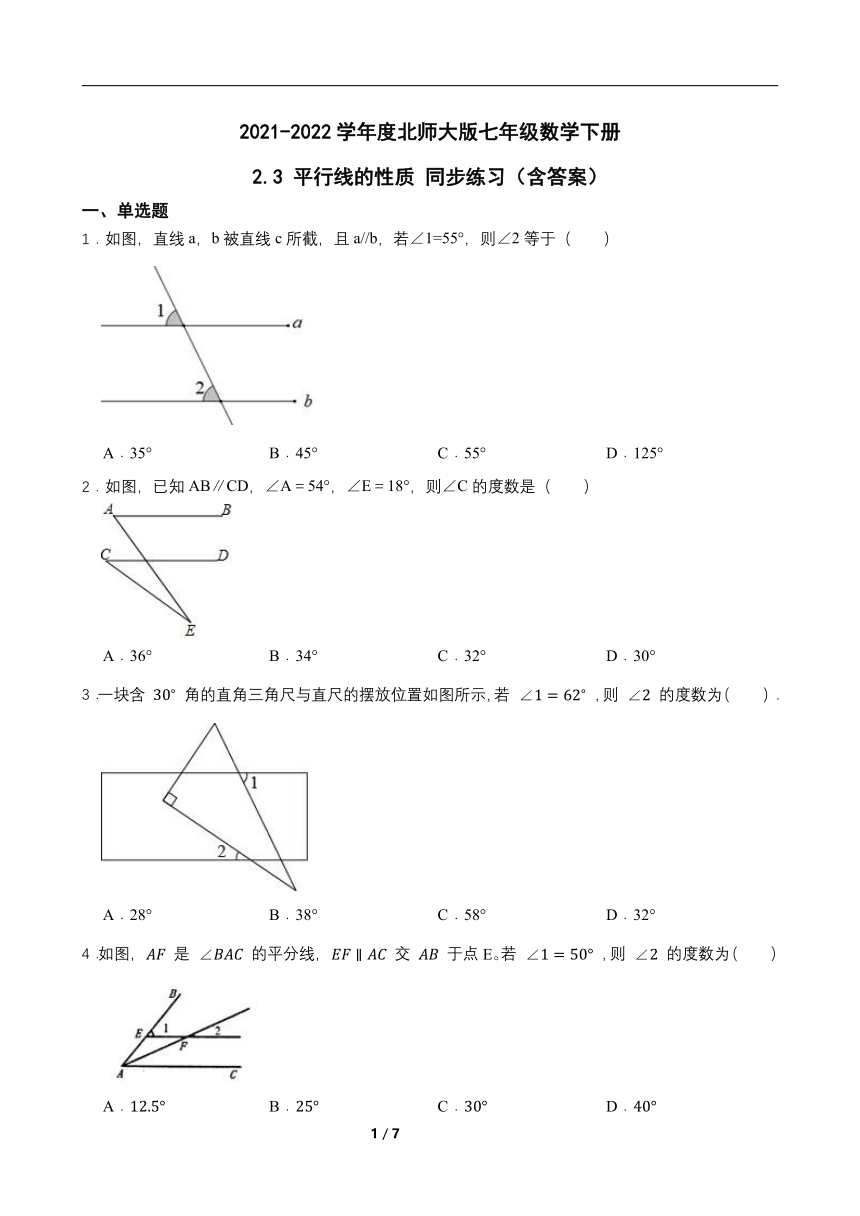
1.如图,直线a,b被直线c所截,且a//b,若∠1=55°,则∠2等于( )
A.35° B.45° C.55° D.125°
2.如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A.36° B.34° C.32° D.30°
3.一块含 角的直角三角尺与直尺的摆放位置如图所示,若 ,则 的度数为( ).
A.28° B.38° C.58° D.32°
4.如图, 是 的平分线, 交 于点E。若 ,则 的度数为( )
A. B. C. D.
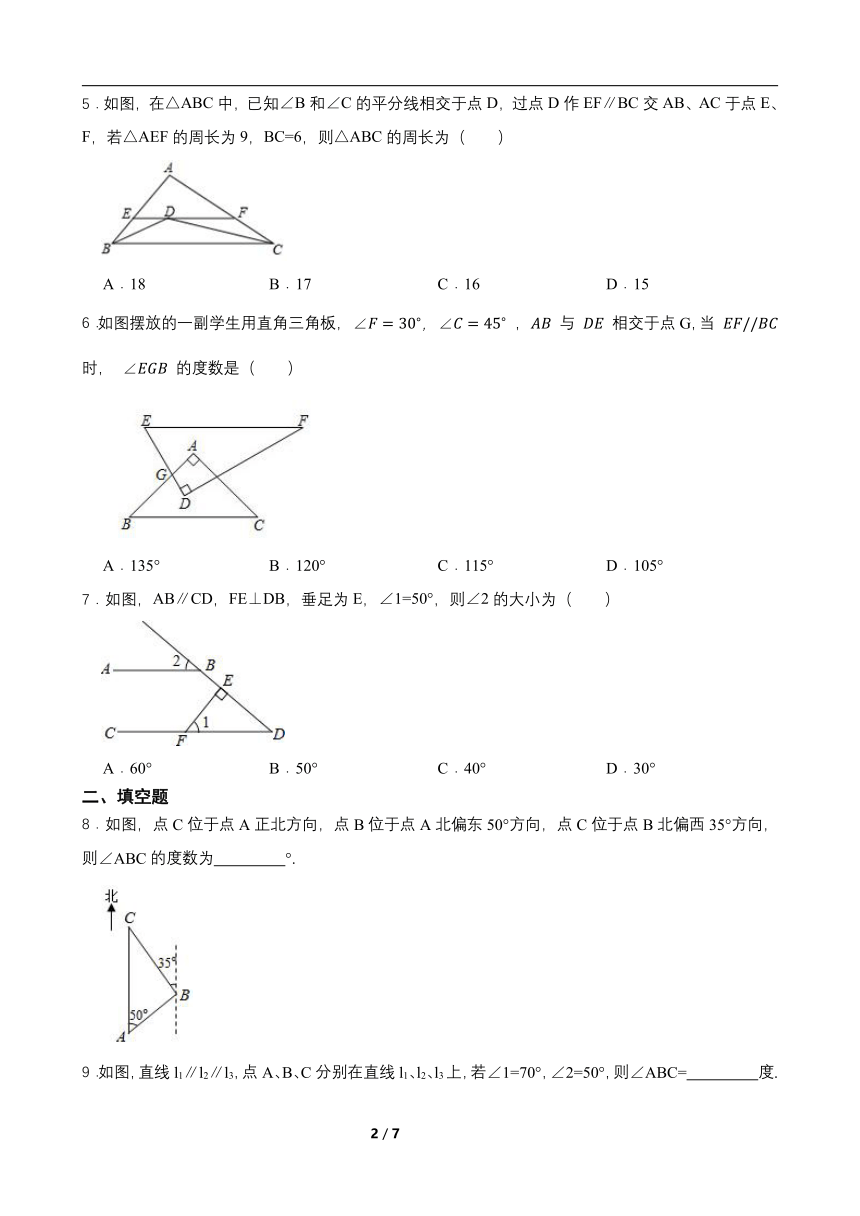
5.如图,在△ABC中,已知∠B和∠C的平分线相交于点D,过点D作EF∥BC交AB、AC于点E、F,若△AEF的周长为9,BC=6,则△ABC的周长为( )
A.18 B.17 C.16 D.15
6.如图摆放的一副学生用直角三角板, , 与 相交于点G,当 时, 的度数是( )
A.135° B.120° C.115° D.105°
7.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的大小为( )
A.60° B.50° C.40° D.30°
二、填空题
8.如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为 °.
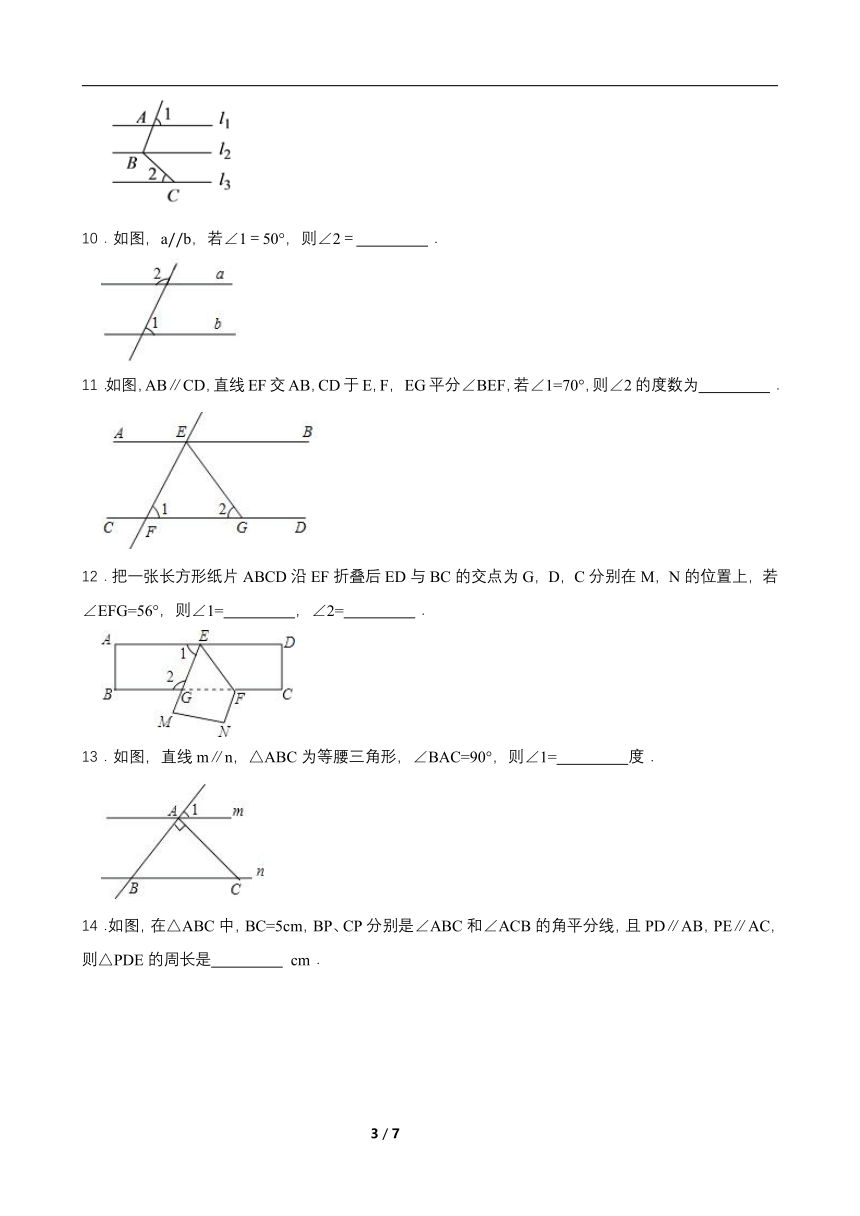
9.如图,直线l1∥l2∥l3,点A、B、C分别在直线l1、l2、l3上,若∠1=70°,∠2=50°,则∠ABC= 度.
10.如图,ab,若∠1=50°,则∠2= .
11.如图,AB∥CD,直线EF交AB,CD于E,F, EG平分∠BEF,若∠1=70°,则∠2的度数为 .
12.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D,C分别在M,N的位置上,若∠EFG=56°,则∠1= ,∠2= .
13.如图,直线m∥n,△ABC为等腰三角形,∠BAC=90°,则∠1= 度.
14.如图,在△ABC中,BC=5cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是 cm.
三、解答题
15.如图,已知 平分 ,且 于 ,点 在同一直线上, ,延长 交 于 ,证明: .
16.如图,在△ABC中,CE平分∠ACB,B、C、G在同一直线上,CF平分∠ACG,EF∥BC交AC于点D,求证:DE= DF.
17.如图,在△ABC中,BE是AC边上的高,DE//BC,∠ADE=48°,∠C=62°,求∠ABE的度数.
18.如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,试说明∠1=∠2的理由.
19.如图所示,点E在直线DF上,点B在直线AC上,直线AF分别交BD,CE于点G,H.若∠AGB=∠EHF,∠C=∠D,请到断∠A与∠F的数量关系,并说明理由.
20.如图,在△ABC中, ∠ABC与 ∠ACB的平分线相交于O.过点O作EF∥BC分别交AB、AC于E、F.若 ∠BOC=130°, ∠ABC: ∠ACB=3:2,求 ∠AEF和 ∠EFC.
答案解析部分
1.C
2.A
3.D
4.B
5.D
6.D
7.C
8.95
9.120
10.130°
11.55°
12.68°;112°
13.45
14.5
15.解: 平分 ,
,
,
,
,
又 ,
.
16.证明:∵CE平分∠ACB,∴∠ACE=∠BCE.
∵CF平分∠ACG,∴∠ACF=∠GCF.
∵EF∥BC,
∴∠GCF=∠F,∠BCE=∠CEFE.∴∠DCE=∠CED,∠F=∠DCF.
∴CD= ED,CD=DF.∴DE=DF.
17.解:∵DE∥BC,∠ADE=48°,
∴∠ABC=∠ADE=48°,
∵BE是AC边上的高,
∴∠BEC =90°,
∵∠C=62°,
∴∠EBC=90°-∠C=28°
∴∠ABE=∠ABC-∠EBC=48°-28°=20°.
18.解:
∵AD⊥BC于D,EG⊥BC于G,
∴AD∥EG,
∴∠1=∠3,∠2=∠E,
∵∠E=∠3,
∴∠1=∠2
19.解:∠A=∠F理由;∵∠AGB=∠DGF(对顶角相等)∠AGB=∠EHF∴∠DGF=∠DGF,∴BD∥CE,∠C=∠ABD,∵∠D=∠C∴∠ABD=∠D∴AC∥DF,∴∠A=∠F
20.解:∵∠ABC: ∠ACB=3:2,
∴设∠ABC=3x, ∠ACB=2x,
∵BO、CO分别平分 ∠ ABC、 ∠ ACB,
∴∠ABO=∠CBO=x,∠ACO=∠BCO=x,
又∵∠BOC=130°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∴130°+x+x=180°,
解得:x=20°,
∴∠ABC=3x=60°, ∠ACB=2x=40°,
∵EF∥BC,
∴∠AEF=∠ABC=60°,
∠EFC+∠ACB=180°,
∴∠EFC=140°.
8 / 8
2.3 平行线的性质 同步练习(含答案)
一、单选题
1.如图,直线a,b被直线c所截,且a//b,若∠1=55°,则∠2等于( )
A.35° B.45° C.55° D.125°
2.如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A.36° B.34° C.32° D.30°
3.一块含 角的直角三角尺与直尺的摆放位置如图所示,若 ,则 的度数为( ).
A.28° B.38° C.58° D.32°
4.如图, 是 的平分线, 交 于点E。若 ,则 的度数为( )
A. B. C. D.
5.如图,在△ABC中,已知∠B和∠C的平分线相交于点D,过点D作EF∥BC交AB、AC于点E、F,若△AEF的周长为9,BC=6,则△ABC的周长为( )
A.18 B.17 C.16 D.15
6.如图摆放的一副学生用直角三角板, , 与 相交于点G,当 时, 的度数是( )
A.135° B.120° C.115° D.105°
7.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的大小为( )
A.60° B.50° C.40° D.30°
二、填空题
8.如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为 °.
9.如图,直线l1∥l2∥l3,点A、B、C分别在直线l1、l2、l3上,若∠1=70°,∠2=50°,则∠ABC= 度.
10.如图,ab,若∠1=50°,则∠2= .
11.如图,AB∥CD,直线EF交AB,CD于E,F, EG平分∠BEF,若∠1=70°,则∠2的度数为 .
12.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D,C分别在M,N的位置上,若∠EFG=56°,则∠1= ,∠2= .
13.如图,直线m∥n,△ABC为等腰三角形,∠BAC=90°,则∠1= 度.
14.如图,在△ABC中,BC=5cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是 cm.
三、解答题
15.如图,已知 平分 ,且 于 ,点 在同一直线上, ,延长 交 于 ,证明: .
16.如图,在△ABC中,CE平分∠ACB,B、C、G在同一直线上,CF平分∠ACG,EF∥BC交AC于点D,求证:DE= DF.
17.如图,在△ABC中,BE是AC边上的高,DE//BC,∠ADE=48°,∠C=62°,求∠ABE的度数.
18.如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,试说明∠1=∠2的理由.
19.如图所示,点E在直线DF上,点B在直线AC上,直线AF分别交BD,CE于点G,H.若∠AGB=∠EHF,∠C=∠D,请到断∠A与∠F的数量关系,并说明理由.
20.如图,在△ABC中, ∠ABC与 ∠ACB的平分线相交于O.过点O作EF∥BC分别交AB、AC于E、F.若 ∠BOC=130°, ∠ABC: ∠ACB=3:2,求 ∠AEF和 ∠EFC.
答案解析部分
1.C
2.A
3.D
4.B
5.D
6.D
7.C
8.95
9.120
10.130°
11.55°
12.68°;112°
13.45
14.5
15.解: 平分 ,
,
,
,
,
又 ,
.
16.证明:∵CE平分∠ACB,∴∠ACE=∠BCE.
∵CF平分∠ACG,∴∠ACF=∠GCF.
∵EF∥BC,
∴∠GCF=∠F,∠BCE=∠CEFE.∴∠DCE=∠CED,∠F=∠DCF.
∴CD= ED,CD=DF.∴DE=DF.
17.解:∵DE∥BC,∠ADE=48°,
∴∠ABC=∠ADE=48°,
∵BE是AC边上的高,
∴∠BEC =90°,
∵∠C=62°,
∴∠EBC=90°-∠C=28°
∴∠ABE=∠ABC-∠EBC=48°-28°=20°.
18.解:
∵AD⊥BC于D,EG⊥BC于G,
∴AD∥EG,
∴∠1=∠3,∠2=∠E,
∵∠E=∠3,
∴∠1=∠2
19.解:∠A=∠F理由;∵∠AGB=∠DGF(对顶角相等)∠AGB=∠EHF∴∠DGF=∠DGF,∴BD∥CE,∠C=∠ABD,∵∠D=∠C∴∠ABD=∠D∴AC∥DF,∴∠A=∠F
20.解:∵∠ABC: ∠ACB=3:2,
∴设∠ABC=3x, ∠ACB=2x,
∵BO、CO分别平分 ∠ ABC、 ∠ ACB,
∴∠ABO=∠CBO=x,∠ACO=∠BCO=x,
又∵∠BOC=130°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∴130°+x+x=180°,
解得:x=20°,
∴∠ABC=3x=60°, ∠ACB=2x=40°,
∵EF∥BC,
∴∠AEF=∠ABC=60°,
∠EFC+∠ACB=180°,
∴∠EFC=140°.
8 / 8
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
