人教版九年级下册26.1.2反比例函数的图象和性质 课件(共16张)
文档属性
| 名称 | 人教版九年级下册26.1.2反比例函数的图象和性质 课件(共16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 314.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
26.1.2反比例函数的图象和性质
复习提问
2. 下列函数中哪些是反比例函数?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1
y = 2x2
y =
x
1
y =
2x
3
y = 3x
y =
x
1
y =
1
3x
y =
3
2x
1. 反比例函数关系式是什么?
x≠0
y≠0
(k ≠0,k是常数)
自变量x的取值范围是什么?
函数y的取值范围是什么?
一次函数y=kx+b(k≠0)的图象是( )
反比例函数 (k≠0 , K是常数)的图象是什么样子呢?性质是什么呢?
一条直线
回顾
思考:
还记得画函数图象的三个步骤是什么?
列表、描点、连线。
x
尝试在坐标纸上画出反比例函数 和 的函数图象。
y =
x
6
y =
x
6
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法画反比例函数图象
活动 1
大胆尝试 ,教师点拨
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
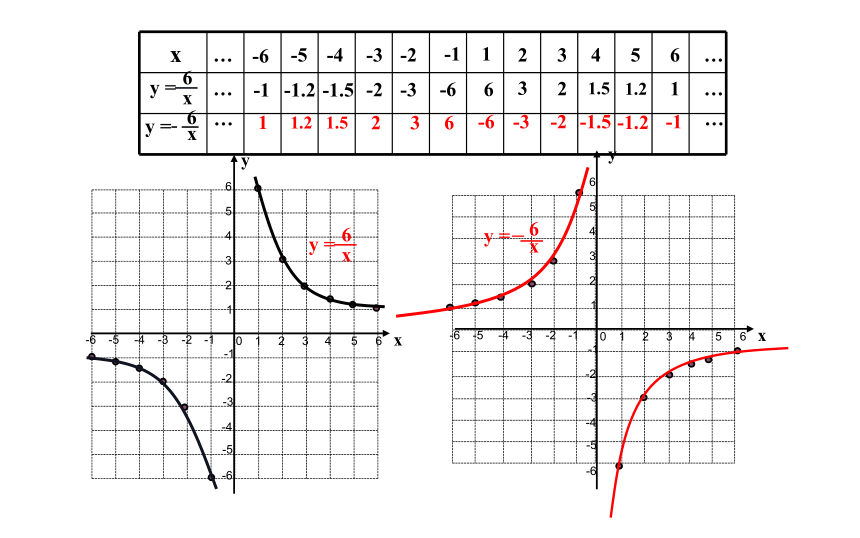
y =
x
6
y =-
x
6
函数图象画法
列
表
描
点
连
线
描点法
心动 不如行动
活动 2
画出反比例函数y= 和 y= - 的函数图象。
观察你所画的函数图象思考:
1、函数y= 与y= 的图象形状? 位置? 函数值y随自变量x是如何变化的?
2、函数y= - 与y= - 的图象形状? 位置? 函数值y随自变量x是如何变化的?
小组互动,知识升华
3、反比例函数 y= (k为常数,k≠0) 的图象形
状?位置?函数值y随自变量x是如何变化的?
y
X
O
k>0
K<0
反比例函数的图象和性质
2、当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。
3、当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。
归纳总结
1、反比例函数 y= (k为常数,k≠0)
的图象是双曲线
当堂练习(一)
2.下列图象中,是反比例函数的图象的是 ( )
1.已知反比例函数y= ( k≠0)的
图象如图所示,则k 0,
在图象的每一支上, y值随x的增大而 .
x
k
>
减小
D
3、函数y= 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
4、 函数y=- 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
5、函数y= ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
1、已知反比例函数y=
若函数的图象位于第一三象限,则k______;
若在每一象限内,y随x增大而增大,则k______.
< 4
> 4
2﹑已知 k<0, 函数 y1=kx, y2= 在同一坐标系中的图象大致是 ( )
x
k
x
x
y
0
x
y
0
(A)
(B)
(C)
(D)
x
y
0
C
当堂练习(二)
我是最棒的
我是最棒的
能力提升
如图,点P是反比例函数
图象上的一点,PD⊥x轴于点D.
则△POD的面积是多少?
y=
2
x
P
D
o
y
x
归纳总结
反比例函数的性质:
1、当k>0时, 图象的两个分支分别在第一、三象限内;在各象限内,函数值y随自变量x的增大而减小。
2、当k<0时, 图象的两个分支分别在第二、四象限内;在各象限内,函数值y随自变量x的增大而增大。
注意:双曲线的两个分支无限接近x轴和y轴,但永远不会与x轴和y轴相交。
对同学说一说这节课你有什么收获?
课后作业:
习题26.1:第3题和第8题.
(选做第9题)
祝同学们学习进步!
谢谢聆听
26.1.2反比例函数的图象和性质
复习提问
2. 下列函数中哪些是反比例函数?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1
y = 2x2
y =
x
1
y =
2x
3
y = 3x
y =
x
1
y =
1
3x
y =
3
2x
1. 反比例函数关系式是什么?
x≠0
y≠0
(k ≠0,k是常数)
自变量x的取值范围是什么?
函数y的取值范围是什么?
一次函数y=kx+b(k≠0)的图象是( )
反比例函数 (k≠0 , K是常数)的图象是什么样子呢?性质是什么呢?
一条直线
回顾
思考:
还记得画函数图象的三个步骤是什么?
列表、描点、连线。
x
尝试在坐标纸上画出反比例函数 和 的函数图象。
y =
x
6
y =
x
6
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法画反比例函数图象
活动 1
大胆尝试 ,教师点拨
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =-
x
6
函数图象画法
列
表
描
点
连
线
描点法
心动 不如行动
活动 2
画出反比例函数y= 和 y= - 的函数图象。
观察你所画的函数图象思考:
1、函数y= 与y= 的图象形状? 位置? 函数值y随自变量x是如何变化的?
2、函数y= - 与y= - 的图象形状? 位置? 函数值y随自变量x是如何变化的?
小组互动,知识升华
3、反比例函数 y= (k为常数,k≠0) 的图象形
状?位置?函数值y随自变量x是如何变化的?
y
X
O
k>0
K<0
反比例函数的图象和性质
2、当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。
3、当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。
归纳总结
1、反比例函数 y= (k为常数,k≠0)
的图象是双曲线
当堂练习(一)
2.下列图象中,是反比例函数的图象的是 ( )
1.已知反比例函数y= ( k≠0)的
图象如图所示,则k 0,
在图象的每一支上, y值随x的增大而 .
x
k
>
减小
D
3、函数y= 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
4、 函数y=- 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
5、函数y= ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
1、已知反比例函数y=
若函数的图象位于第一三象限,则k______;
若在每一象限内,y随x增大而增大,则k______.
< 4
> 4
2﹑已知 k<0, 函数 y1=kx, y2= 在同一坐标系中的图象大致是 ( )
x
k
x
x
y
0
x
y
0
(A)
(B)
(C)
(D)
x
y
0
C
当堂练习(二)
我是最棒的
我是最棒的
能力提升
如图,点P是反比例函数
图象上的一点,PD⊥x轴于点D.
则△POD的面积是多少?
y=
2
x
P
D
o
y
x
归纳总结
反比例函数的性质:
1、当k>0时, 图象的两个分支分别在第一、三象限内;在各象限内,函数值y随自变量x的增大而减小。
2、当k<0时, 图象的两个分支分别在第二、四象限内;在各象限内,函数值y随自变量x的增大而增大。
注意:双曲线的两个分支无限接近x轴和y轴,但永远不会与x轴和y轴相交。
对同学说一说这节课你有什么收获?
课后作业:
习题26.1:第3题和第8题.
(选做第9题)
祝同学们学习进步!
谢谢聆听
