第三单元3.2.2圆锥的体积(课件) 数学六年级下册(共18张PPT)
文档属性
| 名称 | 第三单元3.2.2圆锥的体积(课件) 数学六年级下册(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 997.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
圆锥的认识
人教版六年级下册 第三单元 3.2.1
教学目标
知识目标:推导出圆锥体积的计算公式。
能力目标:运用计算公式求圆锥的体积。
一、复习旧知
日常使用的铅锤是圆锥体吗?
还有哪些物体也是圆锥?
这个小谷堆是一个金黄的圆锥
上节课已认识了圆锥,请大家总结圆锥的特征
二、探究新知
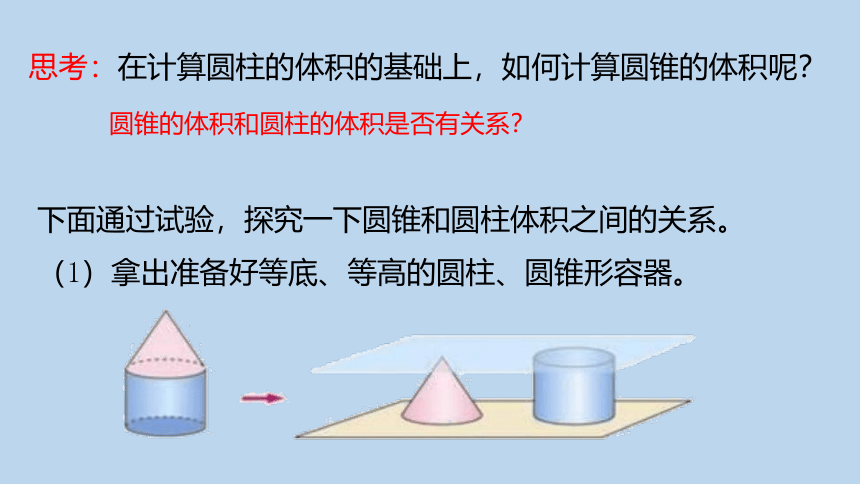
思考:在计算圆柱的体积的基础上,如何计算圆锥的体积呢?
下面通过试验,探究一下圆锥和圆柱体积之间的关系。
(1)拿出准备好等底、等高的圆柱、圆锥形容器。
圆锥的体积和圆柱的体积是否有关系?
(2)用倒水的方法试一试。
三次正好倒满。
我把圆柱装满水,再往圆锥里倒。
正好倒了三次。
(3)通过试验,你发现圆锥的体积与同它等底、等高的圆
柱的体积之间的关系了吗?
圆锥的体积与上面哪一个图形有关呢?
小结
圆锥是一种立体图形,生活中很多物体的形状都是圆锥形。
v=πr2h
1、下图中,圆锥的体积与哪个圆柱的体积相等?说说你是怎么想的。
练习
2、如图,测量中经常使用铅锤。这个铅锤的体积是
多少立方厘米?
≈26.17(cm3)
3、判断。
(1)圆锥的体积等于圆柱体积的 。
(2)圆柱的体积等于与它等底等高的圆锥的体积。
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。
4、如图,这座圆锥形帐篷底面直径约5m,高约3.6m。请计算出它的占地面积和内部的空间。
=23.55(m3)
3.14×(5÷2)2=19.625(m2)
5、圆锥形沙堆底面积是28.26m2,高是2.5m。这堆沙能在10m宽的公路上铺2cm厚的路面铺多少米?
2cm=0.02m
(1)沙堆的体积:
=9.42×2.5
=23.55(m3)
23.55÷10÷0.02
=2.355÷0.02
=117.75(m)
(2)所铺公路的长度
答:能铺117.75m。
×28.26×2.5
3
1
请你想一想,转换前后沙子的体积是否发生变化?
转换前后沙子的体积不变,所以铺成的公路路面的体积等于圆锥形沙堆的体积。
6、 把三角形ABC沿BC边和AB边分别旋转一周,得到2个圆锥(如下图),哪个圆锥的体积大?
以AB边为轴:3×3.14×5 ×3
=3×3.14×25×3
=78.5(cm )
以CB边为轴:3×3.14×3 ×5
=3×3.14×9×5
=47.1(cm )
答:以AB边为轴旋转成圆锥的体积大。
7、一个圆锥的底面直径是8cm,从圆锥的顶点沿着高将它切成相等的两半后,表面积比原来的圆锥增加了48cm .这个圆锥的体积是多少cm
小结
圆锥的体积=底面积×高× ,
用字母表示为V= Sh。
圆锥的认识
人教版六年级下册 第三单元 3.2.1
教学目标
知识目标:推导出圆锥体积的计算公式。
能力目标:运用计算公式求圆锥的体积。
一、复习旧知
日常使用的铅锤是圆锥体吗?
还有哪些物体也是圆锥?
这个小谷堆是一个金黄的圆锥
上节课已认识了圆锥,请大家总结圆锥的特征
二、探究新知
思考:在计算圆柱的体积的基础上,如何计算圆锥的体积呢?
下面通过试验,探究一下圆锥和圆柱体积之间的关系。
(1)拿出准备好等底、等高的圆柱、圆锥形容器。
圆锥的体积和圆柱的体积是否有关系?
(2)用倒水的方法试一试。
三次正好倒满。
我把圆柱装满水,再往圆锥里倒。
正好倒了三次。
(3)通过试验,你发现圆锥的体积与同它等底、等高的圆
柱的体积之间的关系了吗?
圆锥的体积与上面哪一个图形有关呢?
小结
圆锥是一种立体图形,生活中很多物体的形状都是圆锥形。
v=πr2h
1、下图中,圆锥的体积与哪个圆柱的体积相等?说说你是怎么想的。
练习
2、如图,测量中经常使用铅锤。这个铅锤的体积是
多少立方厘米?
≈26.17(cm3)
3、判断。
(1)圆锥的体积等于圆柱体积的 。
(2)圆柱的体积等于与它等底等高的圆锥的体积。
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。
4、如图,这座圆锥形帐篷底面直径约5m,高约3.6m。请计算出它的占地面积和内部的空间。
=23.55(m3)
3.14×(5÷2)2=19.625(m2)
5、圆锥形沙堆底面积是28.26m2,高是2.5m。这堆沙能在10m宽的公路上铺2cm厚的路面铺多少米?
2cm=0.02m
(1)沙堆的体积:
=9.42×2.5
=23.55(m3)
23.55÷10÷0.02
=2.355÷0.02
=117.75(m)
(2)所铺公路的长度
答:能铺117.75m。
×28.26×2.5
3
1
请你想一想,转换前后沙子的体积是否发生变化?
转换前后沙子的体积不变,所以铺成的公路路面的体积等于圆锥形沙堆的体积。
6、 把三角形ABC沿BC边和AB边分别旋转一周,得到2个圆锥(如下图),哪个圆锥的体积大?
以AB边为轴:3×3.14×5 ×3
=3×3.14×25×3
=78.5(cm )
以CB边为轴:3×3.14×3 ×5
=3×3.14×9×5
=47.1(cm )
答:以AB边为轴旋转成圆锥的体积大。
7、一个圆锥的底面直径是8cm,从圆锥的顶点沿着高将它切成相等的两半后,表面积比原来的圆锥增加了48cm .这个圆锥的体积是多少cm
小结
圆锥的体积=底面积×高× ,
用字母表示为V= Sh。
