2021—2022学年人教版九年级数学下册27.2.1相似三角形的判定课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册27.2.1相似三角形的判定课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 276.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览

文档简介
2021——2022学年度人教版九年级数学下册 第二十七章相似
27.2.1相似三角形的判定 课后练习
一、选择题
1.下列说法正确的是( )
A.有两边成比例且有一个角相等的两个三角形相似
B.各有一个角是50°的两个等腰三角形相似
C.有两边对应成比例且夹角相等的两个三角形相似
D.一条直线截三角形两边所得的三角形与原三角形相似
2.如图, 已知在 中, 点 在边 上, 那么下列条件中 不能判定△ABC∽△ACD 的是( )
A. B.
C. D.
3.如图,下列选项中不能判定△ACD∽△ABC的是( )
A.= B.= C.∠ACD=∠B D.∠ADC=∠ACB
4.根据下列条件,判断△ABC与△A′B′C′能相似的条件有( )
①∠C=∠C′=90°,∠A=25°,∠B′=65°;
②∠C=90°,AC=6cm,BC=4cm,,A′C′=9cm,B′C′=6cm;
③AB=10cm,BC=12cm,AC=15cm,A′B′=150cm,B′C′=180cm,A′C′=225cm;
④△ABC与△A′B′C′是有一个角为80°等腰三角形
A.1对 B.2对 C.3对 D.4对
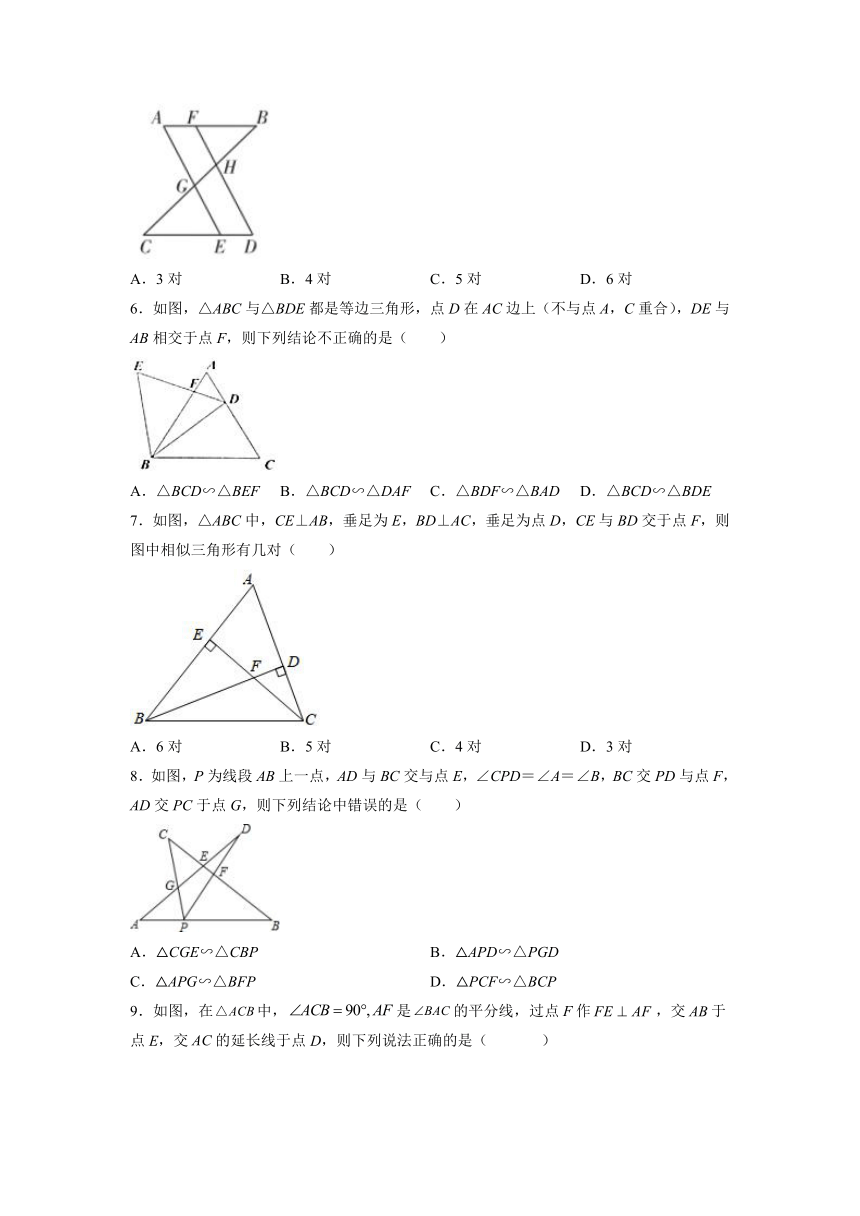
5.如图,,,AE、FD分别交BC于点G、H,则图中的相似三角形共有( )
A.3对 B.4对 C.5对 D.6对
6.如图,△ABC与△BDE都是等边三角形,点D在AC边上(不与点A,C重合),DE与AB相交于点F,则下列结论不正确的是( )
A.△BCD∽△BEF B.△BCD∽△DAF C.△BDF∽△BAD D.△BCD∽△BDE
7.如图,△ABC中,CE⊥AB,垂足为E,BD⊥AC,垂足为点D,CE与BD交于点F,则图中相似三角形有几对( )
A.6对 B.5对 C.4对 D.3对
8.如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC于点G,则下列结论中错误的是( )
A.△CGE∽△CBP B.△APD∽△PGD
C.△APG∽△BFP D.△PCF∽△BCP
9.如图,在中,是的平分线,过点F作,交于点E,交的延长线于点D,则下列说法正确的是( )
A. B. C. D.
10.如图,在中,是边的中点,于点,交边于点,连接,则图中与相似的三角形共有( )
A.个 B.个 C.个 D.个
二、填空题
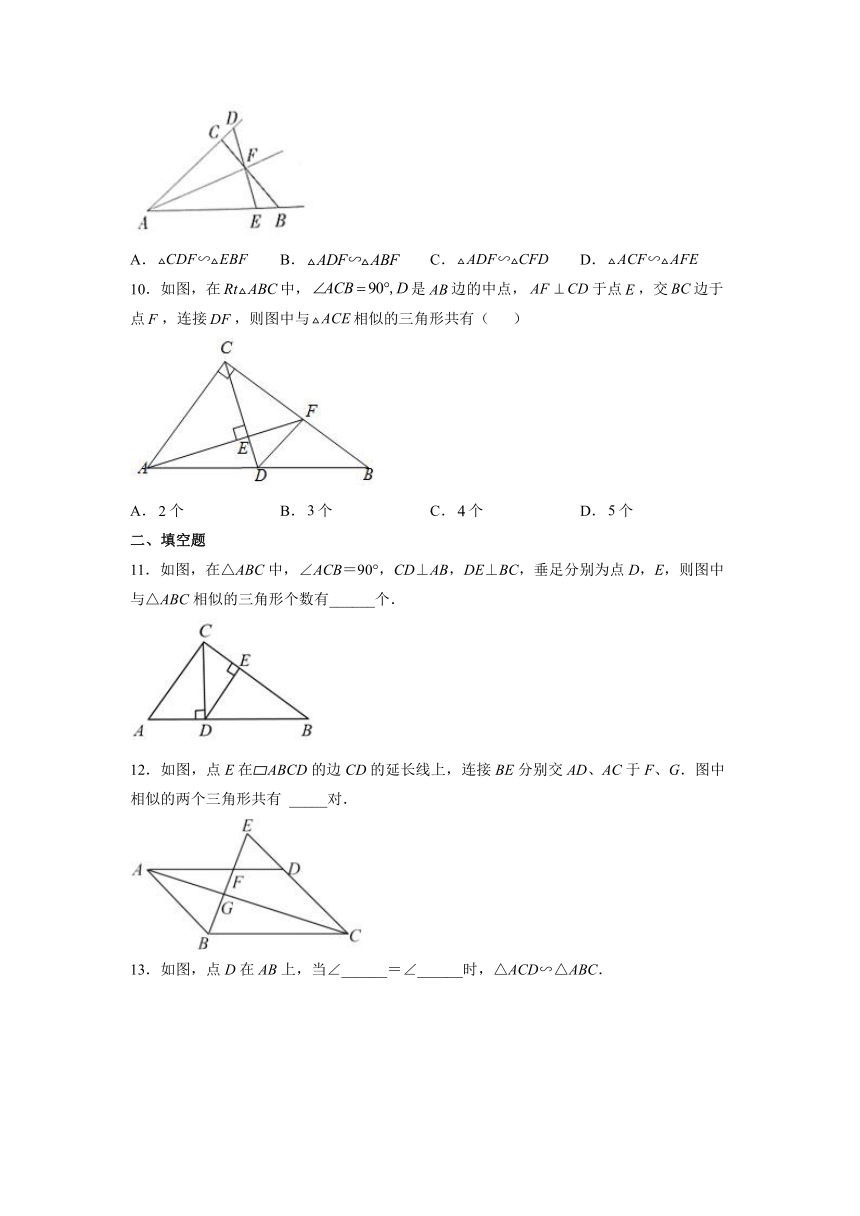
11.如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为点D,E,则图中与△ABC相似的三角形个数有______个.
12.如图,点E在 ABCD的边CD的延长线上,连接BE分别交AD、AC于F、G.图中相似的两个三角形共有 _____对.
13.如图,点D在AB上,当∠______=∠______时,△ACD∽△ABC.
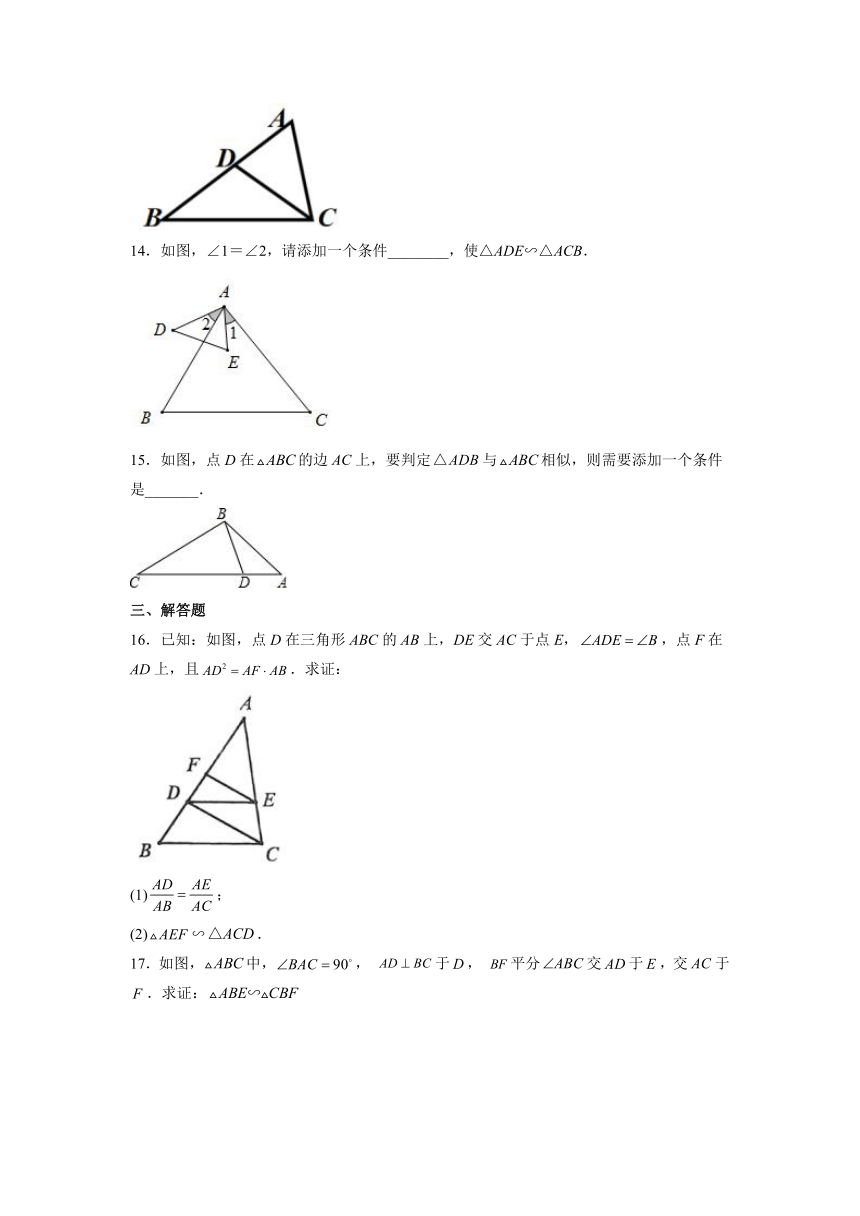
14.如图,∠1=∠2,请添加一个条件________,使△ADE∽△ACB.
15.如图,点D在的边上,要判定与相似,则需要添加一个条件是_______.
三、解答题
16.已知:如图,点D在三角形ABC的AB上,DE交AC于点E,,点F在AD上,且.求证:
(1);
(2)∽.
17.如图,中,, 于, 平分交于,交于.求证:
18.如图,在矩形ABCD中,M为BC上一点,EM⊥AM交AD的延长线于点E.求证:△ABM∽△EMA.
19.如图,在和中,、分别是、上一点,,当时,求证:.
20.如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.求证:△COM∽△CBA.
21.如图,P是的边上的一点.
(1)如果,与是否相似?为什么?
(2)如果,与是否相似?为什么?如果呢?
22.如图,四边形内接于,是的直径,与交于点E,切于点B.
(1)求证:;
(2)若∠PBA=20°,,求证:△OAB∽△CDE.
23.如图1,在矩形中,为边上一点,把沿翻折,使点恰好落在边上的点处.
(1)求证:;
(2)若,,求的长;
(3)如图2,在第(2)问的条件下,若P,Q分别是AE,Ad上的动点,求PD+PQ的最小值.
【参考答案】
1.C 2.A 3.B 4.C 5.D 6.D 7.A 8.A 9.D 10.B
11.4
12.6
13. ACD B
14.∠D=∠C(答案不唯一)
15.(答案不唯一)
16.(1)证明:∵,
∴,
∴,
∴.
(2)证明:∵,
∴,
∵,
∴.
又,
∴∽.
17.证明:∵△ABC中,∠BAC=90°,
∴∠BAD+∠CAD=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠C+∠CAD=90°,
∴∠C=∠BAD,
∵FB平分∠ABC,
∴∠ABF=∠EBD,
∴.
18.证明:矩形ABCD中, ,
,
,
,
,
,
.
19.证明:∵,
∴,
∵,
∴,
∴.
20.证明:∵沿直线MN对折,使A、C重合,
∴A与C关于直线MN对称,
∴AC⊥MN,
∴∠COM=90°,
在矩形ABCD中,∠B=90°,
∴∠COM=∠B,
又∵∠ACB=∠ACB,
∴△COM∽△CBA.
21.解:(1)相似,理由如下:
∵,,
∴;
(2)相似,理由如下:
∵,,
∴;
不相似,理由如下:
因为虽然,但它们的夹角 与 不相等,
所以与不相似.
22.证明:(1)∵是的直径,
∴∠ABC=90°,
∵切于点B,
∴∠OBP=90°,
∴,
∴;
(2)∵,,
∴,
∵OB=OC,
∴,
∴∠AOB=20°+20°=40°,
∵OB=OA,
∴∠OAB=∠OBA=(180°-40°)÷2=70°,
∴∠ADB=∠AOB=20°,
∵是的直径,
∴∠ADC=90°,
∴∠CDE=90°-20°=70°,
∴∠CDE=∠OAB,
∵,
∴,
∴.
23.(1)证明:∵四边形是矩形,
∴,
∴,
∵由翻折得到,
∴,
∴,
∴,,
∴;
(2)∵四边形是矩形,
∴,.
设,则,
在中,,
∴,
在中,,即,
解得,即.
(3)如图,根据折叠的性质,点F、D关于直线AE对称,过F作FQ⊥AD于Q,交AE于P,此时PD+PQ的最小值为FQ,
∵四边形ABCD是矩形,
∴∠C=∠ADC=90,又FQ⊥AD,
∴四边形QFCD是矩形,
∴FQ=CD=AB=3,
∴PD+PQ的最小值为
27.2.1相似三角形的判定 课后练习
一、选择题
1.下列说法正确的是( )
A.有两边成比例且有一个角相等的两个三角形相似
B.各有一个角是50°的两个等腰三角形相似
C.有两边对应成比例且夹角相等的两个三角形相似
D.一条直线截三角形两边所得的三角形与原三角形相似
2.如图, 已知在 中, 点 在边 上, 那么下列条件中 不能判定△ABC∽△ACD 的是( )
A. B.
C. D.
3.如图,下列选项中不能判定△ACD∽△ABC的是( )
A.= B.= C.∠ACD=∠B D.∠ADC=∠ACB
4.根据下列条件,判断△ABC与△A′B′C′能相似的条件有( )
①∠C=∠C′=90°,∠A=25°,∠B′=65°;
②∠C=90°,AC=6cm,BC=4cm,,A′C′=9cm,B′C′=6cm;
③AB=10cm,BC=12cm,AC=15cm,A′B′=150cm,B′C′=180cm,A′C′=225cm;
④△ABC与△A′B′C′是有一个角为80°等腰三角形
A.1对 B.2对 C.3对 D.4对
5.如图,,,AE、FD分别交BC于点G、H,则图中的相似三角形共有( )
A.3对 B.4对 C.5对 D.6对
6.如图,△ABC与△BDE都是等边三角形,点D在AC边上(不与点A,C重合),DE与AB相交于点F,则下列结论不正确的是( )
A.△BCD∽△BEF B.△BCD∽△DAF C.△BDF∽△BAD D.△BCD∽△BDE
7.如图,△ABC中,CE⊥AB,垂足为E,BD⊥AC,垂足为点D,CE与BD交于点F,则图中相似三角形有几对( )
A.6对 B.5对 C.4对 D.3对
8.如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC于点G,则下列结论中错误的是( )
A.△CGE∽△CBP B.△APD∽△PGD
C.△APG∽△BFP D.△PCF∽△BCP
9.如图,在中,是的平分线,过点F作,交于点E,交的延长线于点D,则下列说法正确的是( )
A. B. C. D.
10.如图,在中,是边的中点,于点,交边于点,连接,则图中与相似的三角形共有( )
A.个 B.个 C.个 D.个
二、填空题
11.如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为点D,E,则图中与△ABC相似的三角形个数有______个.
12.如图,点E在 ABCD的边CD的延长线上,连接BE分别交AD、AC于F、G.图中相似的两个三角形共有 _____对.
13.如图,点D在AB上,当∠______=∠______时,△ACD∽△ABC.
14.如图,∠1=∠2,请添加一个条件________,使△ADE∽△ACB.
15.如图,点D在的边上,要判定与相似,则需要添加一个条件是_______.
三、解答题
16.已知:如图,点D在三角形ABC的AB上,DE交AC于点E,,点F在AD上,且.求证:
(1);
(2)∽.
17.如图,中,, 于, 平分交于,交于.求证:
18.如图,在矩形ABCD中,M为BC上一点,EM⊥AM交AD的延长线于点E.求证:△ABM∽△EMA.
19.如图,在和中,、分别是、上一点,,当时,求证:.
20.如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.求证:△COM∽△CBA.
21.如图,P是的边上的一点.
(1)如果,与是否相似?为什么?
(2)如果,与是否相似?为什么?如果呢?
22.如图,四边形内接于,是的直径,与交于点E,切于点B.
(1)求证:;
(2)若∠PBA=20°,,求证:△OAB∽△CDE.
23.如图1,在矩形中,为边上一点,把沿翻折,使点恰好落在边上的点处.
(1)求证:;
(2)若,,求的长;
(3)如图2,在第(2)问的条件下,若P,Q分别是AE,Ad上的动点,求PD+PQ的最小值.
【参考答案】
1.C 2.A 3.B 4.C 5.D 6.D 7.A 8.A 9.D 10.B
11.4
12.6
13. ACD B
14.∠D=∠C(答案不唯一)
15.(答案不唯一)
16.(1)证明:∵,
∴,
∴,
∴.
(2)证明:∵,
∴,
∵,
∴.
又,
∴∽.
17.证明:∵△ABC中,∠BAC=90°,
∴∠BAD+∠CAD=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠C+∠CAD=90°,
∴∠C=∠BAD,
∵FB平分∠ABC,
∴∠ABF=∠EBD,
∴.
18.证明:矩形ABCD中, ,
,
,
,
,
,
.
19.证明:∵,
∴,
∵,
∴,
∴.
20.证明:∵沿直线MN对折,使A、C重合,
∴A与C关于直线MN对称,
∴AC⊥MN,
∴∠COM=90°,
在矩形ABCD中,∠B=90°,
∴∠COM=∠B,
又∵∠ACB=∠ACB,
∴△COM∽△CBA.
21.解:(1)相似,理由如下:
∵,,
∴;
(2)相似,理由如下:
∵,,
∴;
不相似,理由如下:
因为虽然,但它们的夹角 与 不相等,
所以与不相似.
22.证明:(1)∵是的直径,
∴∠ABC=90°,
∵切于点B,
∴∠OBP=90°,
∴,
∴;
(2)∵,,
∴,
∵OB=OC,
∴,
∴∠AOB=20°+20°=40°,
∵OB=OA,
∴∠OAB=∠OBA=(180°-40°)÷2=70°,
∴∠ADB=∠AOB=20°,
∵是的直径,
∴∠ADC=90°,
∴∠CDE=90°-20°=70°,
∴∠CDE=∠OAB,
∵,
∴,
∴.
23.(1)证明:∵四边形是矩形,
∴,
∴,
∵由翻折得到,
∴,
∴,
∴,,
∴;
(2)∵四边形是矩形,
∴,.
设,则,
在中,,
∴,
在中,,即,
解得,即.
(3)如图,根据折叠的性质,点F、D关于直线AE对称,过F作FQ⊥AD于Q,交AE于P,此时PD+PQ的最小值为FQ,
∵四边形ABCD是矩形,
∴∠C=∠ADC=90,又FQ⊥AD,
∴四边形QFCD是矩形,
∴FQ=CD=AB=3,
∴PD+PQ的最小值为
