2021—2022学年人教版九年级数学下册27.2相似三角形课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册27.2相似三角形课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 247.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览



文档简介
2021——2022学年度人教版九年级数学下册 第二十七章 相似 27.2相似三角形课后练习
一、选择题
1.下列各组图形必相似的是( ).A.任意两个等腰三角形 B.两条边之比为2∶3的两个直角三角形
C.两条边成比例的两个直角三角形 D.斜边和一条直角边对应成比例的两个直角三角形
2.在中,D为边上一点,则下列条件一定能得到一对相似三角形的是( )
A. B. C. D.
3.点P是△ABC中AB边上一点(不与A、B重合),过P作直线截△ABC使得截得的三角形与△ABC相似,这样的直线最多作( )
A.2条 B.3条 C.4条 D.5条
4.若,顶点A、B、C分别与D、E、F对应,且,则这两个三角形的对应中线之比为( )
A. B. C. D.
5.如果两个相似三角形对应边的比为1:4,那么它们的周长比是( )
A.1:2 B.1:4 C.1:8 D.1:16
6.如图,已知,若,,,则AC的长是( )
A.12 B.13 C.14 D.15
7.如图,△ABC中,,,则△ADE与△ABC的面积比为( )
A.2:3 B.2:5 C.4:9 D.4:25
8.如图,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点.若△DCE和△ABC相似,则线段CE的长为( )
A. B. C.或3 D.或4
9.如图,中,,是中线, 是上一点,作射线,交于点,若,则 ( )
A. B. C. D.
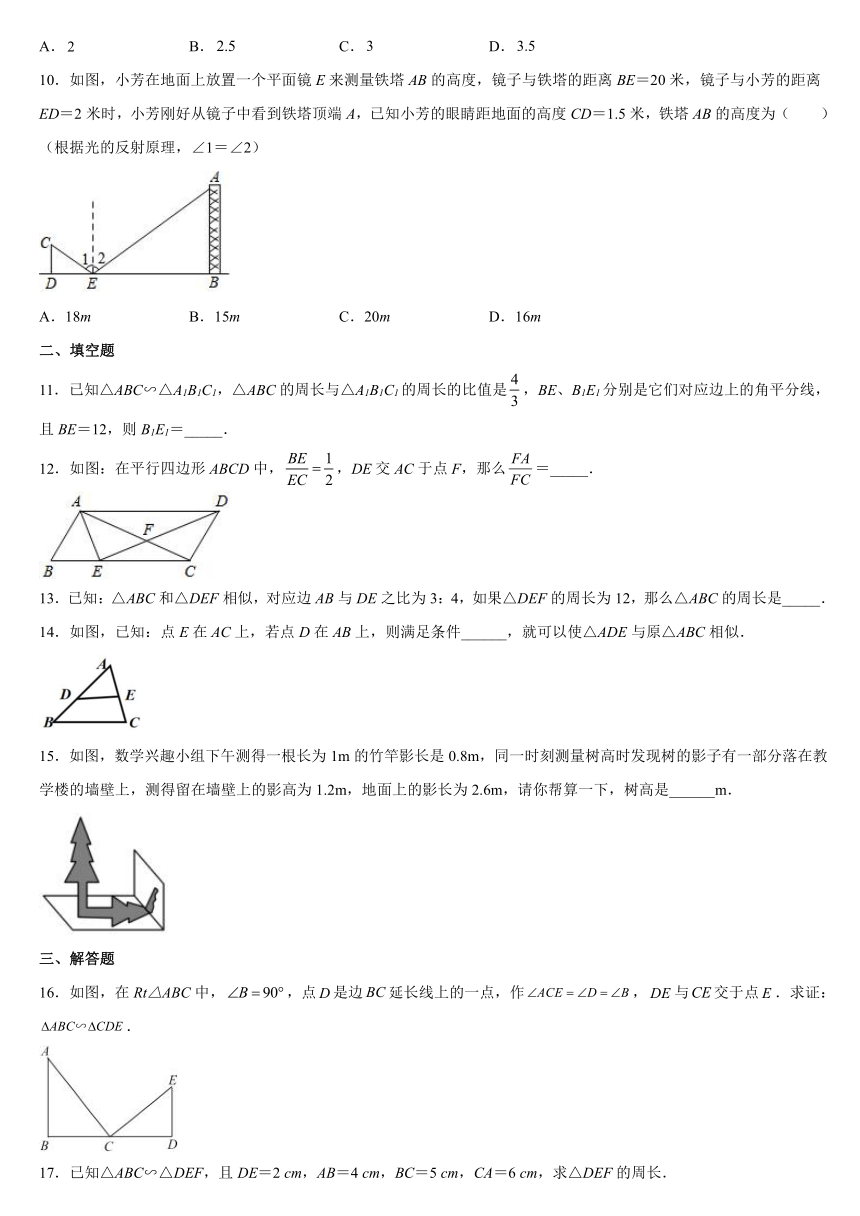
10.如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m B.15m C.20m D.16m
二、填空题
11.已知△ABC∽△A1B1C1,△ABC的周长与△A1B1C1的周长的比值是,BE、B1E1分别是它们对应边上的角平分线,且BE=12,则B1E1=_____.
12.如图:在平行四边形ABCD中,,DE交AC于点F,那么=_____.
13.已知:△ABC和△DEF相似,对应边AB与DE之比为3:4,如果△DEF的周长为12,那么△ABC的周长是_____.
14.如图,已知:点E在AC上,若点D在AB上,则满足条件______,就可以使△ADE与原△ABC相似.
15.如图,数学兴趣小组下午测得一根长为1m的竹竿影长是0.8m,同一时刻测量树高时发现树的影子有一部分落在教学楼的墙壁上,测得留在墙壁上的影高为1.2m,地面上的影长为2.6m,请你帮算一下,树高是______m.
三、解答题
16.如图,在Rt△ABC中,,点是边延长线上的一点,作,与交于点.求证:.
17.已知△ABC∽△DEF,且DE=2 cm,AB=4 cm,BC=5 cm,CA=6 cm,求△DEF的周长.
18.如图,中,,在上分别截取的延长线相交于点F,证明:.
19.如图,在△ABC中,D在AC上,DE∥BC,DF∥AB.
(1)求证:△DFC∽△AED;
(2)若CD=AC,求S△DFC/S△AED的值.
20.如图,在中,,,,为的中点;在上有一点,直线和直线交于点,.
(1)当在的延长线上时,记,试求关于的解析式,并求出的取值范围.
(2)当取什么值的时候,和相似?
21.如图,与交于D,F两点,是直径,.
(1)证明:;
(2)若,求的长度.
22.如图,已知△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,BF、ED的延长线交于点G,连接GC.
(1)求证:AB=GD;
(2)当CG=EG时,且AB=2,求CE.
23.如图,小明和同伴发现在某地小山坡的点E处有一座亭子,他们想利用皮尺、测倾器测量亭子到山脚下的距离(即DE的长度),小明站在点B处,同伴移动侧倾器至点C处时,测得小明头顶A和亭子E的仰角∠ACB=∠ECD(侧倾器的高度忽略不计).已知:AB⊥BC,BC=6米,CD=22米,∠CDE=135°.已知小明的身高AB=1.6米,请根据以上数据,求DE的长度.
【参考答案】
1.D 2.C 3.C 4.B 5.B 6.A 7.D 8.C 9.C 10.B
11.9
12.1.5
13.9
14.DE//BC(或者∠B=∠ADE ) (或者∠C=∠AED )
15.4.45
16.解:∵,
∴,
∴,
又∵,
∴.
17.解:△ABC的周长=AB+BC+CA=4+5+6=15(cm),
∵△ABC∽△DEF,
∴,
∴△DEF的周长=×15=7.5(cm).
18.如图,过点E作 交BC于点M,
∵,
∴ ,,
∴ ,
∴ ,
即 ,
∵
∴ ,
∴,
∴
19.(1)证:∵DE∥BC,
∴∠AED=∠B,∠ADE=∠C,
∵DF∥AB,
∴∠DFC=∠B,
∴∠AED=∠DFC,
∵∠AED=∠DFC,∠ADE=∠C,
∴△DFC∽△AED;
(2)解:∵CD=AC,
∴CD=AD,即:,
∵△DFC∽△AED,
∴△DFC与△AED的相似比为,
∴.
20.(1)如图,延长MP至R,连接CR,使RC∥AB
∵M为BC中点,
∴≌(AAS)
∴RC=BQ=y,
令∠ACB=,则∠RCM=∠QBM=90°+,
∴∠PCR=90°
∵RC//AB,
∴∽
∴ 即,整理得
(2)(i)当点Q在AB延长线上时
因为∠BMQ=∠CMP,∠QBM>90°,
∴∠QBM=∠CPM,∠Q=,
因为∠ABC=∠APQ,
∴∽,
∴,即
所以,解得
(ii)当点Q在BA延长线上时
若和相似,则∠ACB=∠Q,
所以∠QBM=∠CPM=∠APQ,
∴△ABC∽△MBQ∽△APQ∽△MPC
∴△ABC∽△MPC
所以,即,所以
综上所述,当或时,和相似.
21.(1)证明:
四边形是的内接四边形
(2)
,
即
解得
22.解:∵D,E是AC,BC的中点,
∴DE为△ABC的中位线,
∴DE∥AB,AB=2DE,
∴∠ABF=∠DGF,
∵F为AD中点,
∴AF=DF,
在△ABF和△DGF中,
∴△ABF≌△DGF(AAS),
∴AB=GD;
(2)∵AB=2,
∴CD=2,DE=1,
∴GE=3,
∵CA=CB,
∴∠CAB=∠CBA,
∵CG=EG,
∴∠GEC=∠GCE,
∵DE∥AB,
∴∠GEC=∠CBA,
∴△GEC∽△CBA,
设CE=x,
则BC=2x,
∴,即,
解得:,(负值舍去)
∴CE=.
23.解:过E作EF⊥BC于F,
∵∠CDE=135°,
∴∠EDF=45°,
设EF为x米,DF=x米,DE=x米,
∵∠B=∠EFC=90°,
∵∠ACB=∠ECD,
∴△ABC∽△EFC,
∴,
即,
解得:x=8,
经检验:是原方程的根,且符合题意,
∴DE=,
答:DE的长度为米.
一、选择题
1.下列各组图形必相似的是( ).A.任意两个等腰三角形 B.两条边之比为2∶3的两个直角三角形
C.两条边成比例的两个直角三角形 D.斜边和一条直角边对应成比例的两个直角三角形
2.在中,D为边上一点,则下列条件一定能得到一对相似三角形的是( )
A. B. C. D.
3.点P是△ABC中AB边上一点(不与A、B重合),过P作直线截△ABC使得截得的三角形与△ABC相似,这样的直线最多作( )
A.2条 B.3条 C.4条 D.5条
4.若,顶点A、B、C分别与D、E、F对应,且,则这两个三角形的对应中线之比为( )
A. B. C. D.
5.如果两个相似三角形对应边的比为1:4,那么它们的周长比是( )
A.1:2 B.1:4 C.1:8 D.1:16
6.如图,已知,若,,,则AC的长是( )
A.12 B.13 C.14 D.15
7.如图,△ABC中,,,则△ADE与△ABC的面积比为( )
A.2:3 B.2:5 C.4:9 D.4:25
8.如图,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点.若△DCE和△ABC相似,则线段CE的长为( )
A. B. C.或3 D.或4
9.如图,中,,是中线, 是上一点,作射线,交于点,若,则 ( )
A. B. C. D.
10.如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m B.15m C.20m D.16m
二、填空题
11.已知△ABC∽△A1B1C1,△ABC的周长与△A1B1C1的周长的比值是,BE、B1E1分别是它们对应边上的角平分线,且BE=12,则B1E1=_____.
12.如图:在平行四边形ABCD中,,DE交AC于点F,那么=_____.
13.已知:△ABC和△DEF相似,对应边AB与DE之比为3:4,如果△DEF的周长为12,那么△ABC的周长是_____.
14.如图,已知:点E在AC上,若点D在AB上,则满足条件______,就可以使△ADE与原△ABC相似.
15.如图,数学兴趣小组下午测得一根长为1m的竹竿影长是0.8m,同一时刻测量树高时发现树的影子有一部分落在教学楼的墙壁上,测得留在墙壁上的影高为1.2m,地面上的影长为2.6m,请你帮算一下,树高是______m.
三、解答题
16.如图,在Rt△ABC中,,点是边延长线上的一点,作,与交于点.求证:.
17.已知△ABC∽△DEF,且DE=2 cm,AB=4 cm,BC=5 cm,CA=6 cm,求△DEF的周长.
18.如图,中,,在上分别截取的延长线相交于点F,证明:.
19.如图,在△ABC中,D在AC上,DE∥BC,DF∥AB.
(1)求证:△DFC∽△AED;
(2)若CD=AC,求S△DFC/S△AED的值.
20.如图,在中,,,,为的中点;在上有一点,直线和直线交于点,.
(1)当在的延长线上时,记,试求关于的解析式,并求出的取值范围.
(2)当取什么值的时候,和相似?
21.如图,与交于D,F两点,是直径,.
(1)证明:;
(2)若,求的长度.
22.如图,已知△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,BF、ED的延长线交于点G,连接GC.
(1)求证:AB=GD;
(2)当CG=EG时,且AB=2,求CE.
23.如图,小明和同伴发现在某地小山坡的点E处有一座亭子,他们想利用皮尺、测倾器测量亭子到山脚下的距离(即DE的长度),小明站在点B处,同伴移动侧倾器至点C处时,测得小明头顶A和亭子E的仰角∠ACB=∠ECD(侧倾器的高度忽略不计).已知:AB⊥BC,BC=6米,CD=22米,∠CDE=135°.已知小明的身高AB=1.6米,请根据以上数据,求DE的长度.
【参考答案】
1.D 2.C 3.C 4.B 5.B 6.A 7.D 8.C 9.C 10.B
11.9
12.1.5
13.9
14.DE//BC(或者∠B=∠ADE ) (或者∠C=∠AED )
15.4.45
16.解:∵,
∴,
∴,
又∵,
∴.
17.解:△ABC的周长=AB+BC+CA=4+5+6=15(cm),
∵△ABC∽△DEF,
∴,
∴△DEF的周长=×15=7.5(cm).
18.如图,过点E作 交BC于点M,
∵,
∴ ,,
∴ ,
∴ ,
即 ,
∵
∴ ,
∴,
∴
19.(1)证:∵DE∥BC,
∴∠AED=∠B,∠ADE=∠C,
∵DF∥AB,
∴∠DFC=∠B,
∴∠AED=∠DFC,
∵∠AED=∠DFC,∠ADE=∠C,
∴△DFC∽△AED;
(2)解:∵CD=AC,
∴CD=AD,即:,
∵△DFC∽△AED,
∴△DFC与△AED的相似比为,
∴.
20.(1)如图,延长MP至R,连接CR,使RC∥AB
∵M为BC中点,
∴≌(AAS)
∴RC=BQ=y,
令∠ACB=,则∠RCM=∠QBM=90°+,
∴∠PCR=90°
∵RC//AB,
∴∽
∴ 即,整理得
(2)(i)当点Q在AB延长线上时
因为∠BMQ=∠CMP,∠QBM>90°,
∴∠QBM=∠CPM,∠Q=,
因为∠ABC=∠APQ,
∴∽,
∴,即
所以,解得
(ii)当点Q在BA延长线上时
若和相似,则∠ACB=∠Q,
所以∠QBM=∠CPM=∠APQ,
∴△ABC∽△MBQ∽△APQ∽△MPC
∴△ABC∽△MPC
所以,即,所以
综上所述,当或时,和相似.
21.(1)证明:
四边形是的内接四边形
(2)
,
即
解得
22.解:∵D,E是AC,BC的中点,
∴DE为△ABC的中位线,
∴DE∥AB,AB=2DE,
∴∠ABF=∠DGF,
∵F为AD中点,
∴AF=DF,
在△ABF和△DGF中,
∴△ABF≌△DGF(AAS),
∴AB=GD;
(2)∵AB=2,
∴CD=2,DE=1,
∴GE=3,
∵CA=CB,
∴∠CAB=∠CBA,
∵CG=EG,
∴∠GEC=∠GCE,
∵DE∥AB,
∴∠GEC=∠CBA,
∴△GEC∽△CBA,
设CE=x,
则BC=2x,
∴,即,
解得:,(负值舍去)
∴CE=.
23.解:过E作EF⊥BC于F,
∵∠CDE=135°,
∴∠EDF=45°,
设EF为x米,DF=x米,DE=x米,
∵∠B=∠EFC=90°,
∵∠ACB=∠ECD,
∴△ABC∽△EFC,
∴,
即,
解得:x=8,
经检验:是原方程的根,且符合题意,
∴DE=,
答:DE的长度为米.
