2021-2022学年苏科版七年级数学下册7.4认识三角形课前预习练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7.4认识三角形课前预习练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 331.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览




文档简介
7.4认识三角形
一、选择题
1、小明作△ABC中AC边上的高线,下列三角板的摆放位置正确的是( )
A.B. C.D.
2.能将一个三角形分成面积相等的两个三角形的一条线段是( )
A. 三角形的高线 B. 边的中垂线 C. 三角形的中线 D. 三角形的角平分线
3.在下列各图的△ABC中,正确画出AC边上的高的图形是( )
A. B.
C. D.
4.下列说法错误的是( )
A. 任意三角形都有三条高线、中线、角平分线
B. 钝角三角形有两条高线在三角形的外部
C. 直角三角形只有一条高线
D. 锐角三角形的三条高线、三条中线、三条角平分线分别交于一点
5、袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
6.在中作边上的高,下列画法正确的是( )
A. B.
C. D.
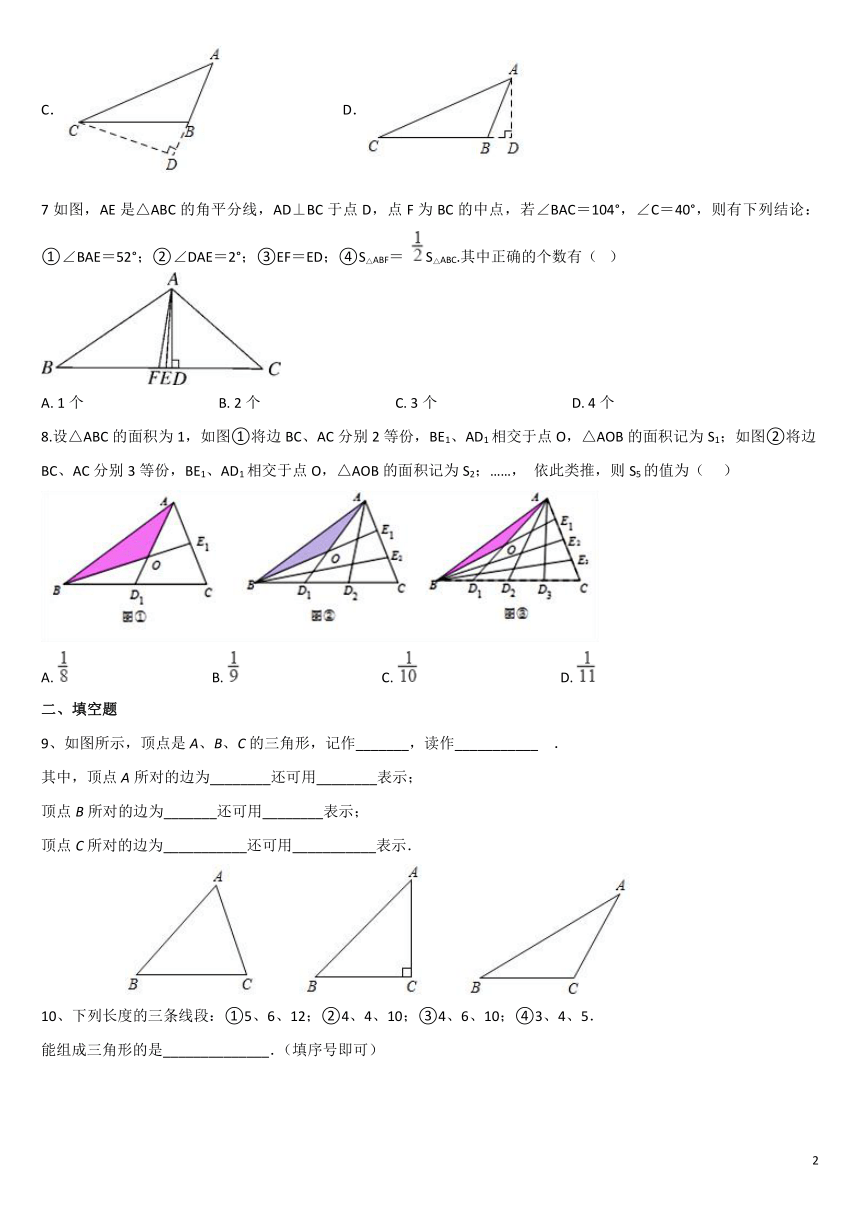
7如图,AE是△ABC的角平分线,AD⊥BC于点D,点F为BC的中点,若∠BAC=104°,∠C=40°,则有下列结论:①∠BAE=52°;②∠DAE=2°;③EF=ED;④S△ABF= S△ABC.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
8.设△ABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……, 依此类推,则S5的值为( )
A. B. C. D.
二、填空题
9、如图所示,顶点是A、B、C的三角形,记作_______,读作___________ .
其中,顶点A所对的边为________还可用________表示;
顶点B所对的边为_______还可用________表示;
顶点C所对的边为___________还可用___________表示.
10、下列长度的三条线段:①5、6、12;②4、4、10;③4、6、10;④3、4、5.
能组成三角形的是______________.(填序号即可)
11.如图,已知是的中线,,,和的周长的差是__________.
12.如图,三边的中线、、相交于点若,则图中阴影部分的面积之和为 .
13.如图,在中,已知点为边上一点,、分别为边、的中点,且,则______.
14.△ABC中,AB=AC,一腰上的中线BD把三角形的周长分为9cm和12cm两部分,则此三角形的腰长是________.
15.如图,△ABC的面积为49cm2 , AE=ED,BD=3DC,则图中△AEF的面积等于________.
16.如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为4、5、7,四边形DHOG面积为________.
三、解答题
17、已知:如图,试回答下列问题:
(1)图中有_______个三角形,其中直角三角形是______.
(2)以线段AC为公共边的三角形是___________.
(3)线段CD所在的三角形是_______,BD边所对的角是________.
(4)、、这三个三角形的面积之比等于_______.
18.如图,在△ABC中,点D、E分别为BC、AD的中点,若S△ABC=1,求S△ABE .
19如图,AD为△ABC的中线,BE为△ABD的中线,过点E作EF垂直BC,垂足为点F.
(1)∠ABE=15 ,∠BAD=55 ,求∠BED的度数;
(2)若△ABC的面积为30,EF=5,求CD.
20如图,在△ABC中,AD⊥BC,AE平分∠BAC
(1)若∠B=70°,∠C=30°,求;
①∠BAE的度数.
②∠DAE的度数.
(2)探究:如果只知道∠B=∠C+40°,那么能求岀∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
21、如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.
1.D.
2.C.
3.C.
4.C.
5.D.
6.C
7.C
8.D
9、 三角形ABC BC a AC b AB c
10:④.
11.【答案】
12.【答案】
13.【答案】
14【答案】8cm或6cm
【考点】三角形三边关系
解:根据题意画出图形,如图,
设等腰三角形的腰长AB=AC=2x,BC=y,
∵BD是腰上的中线,
∴AD=DC=x,
若AB+AD的长为12,则2x+x=12,解得x=4cm,
则x+y=9,即4+y=9,解得y=5cm;
若AB+AD的长为9,则2x+x=9,解得x=3cm,
则x+y=12,即3+y=12,解得y=9cm;
所以等腰三角形的腰长为8cm或6cm.
故答案为:8cm或6cm.
【分析】由于本题没有说明把三角形分成两部分后哪部分长为9cm或12cm,所以需分情况说明,当AB+=9时,AB=6cm,因为三角形的周长为21cm,所以底边长为9cm,6+6>9,所以成立. 当时,AB=8cm,底边长为5cm,因为8+8>5,所以成立.
15.【答案】
【考点】三角形的面积
解:如图:
∵BD=3DC,△ABC的面积为49cm2 ,
∴S△ABD=S△ABC=cm2 , S△ADC=S△ABC=cm2,
∵AE=ED,
∴S△BED=S△ABD=cm2 , S△AEF=S△EFD ,
∴S△BDF=S△BED+S△AEF=+S△AEF ,
∵BD=3DC,
∴S△FDC=S△BDF=+S△AEF ,
∵S△ADC=S△AEF+S△EFD+S△FDC ,
∴=2S△AEF++S△AEF ,
∴S△AEF=cm2.
故答案为: .
【分析】连接DF,根据AE=ED,BD=3DC,及同高三角形的面积的关系得出S△AEF=S△EFD , S△ABE=S△BED , S△BDF=3S△FDC , S△ABD=3S△ADC , 根据△ABC的面积等于49cm2即可得出S△ABD=S△ABC=cm2 , S△ADC=S△ABC=cm2,S△BED=S△ABD=cm2 , S△BDF=S△BED+S△AEF=+S△AEF , S△FDC=S△BDF=+S△AEF , 最后根据S△ADC=S△AEF+S△EFD+S△FDC , 建立方程,求解即可.
16.【答案】 6
【考点】三角形的面积
解:连接OC,OB,OA,OD,
∵E、F、G、H依次是各边中点,
∴△AOE和△BOE等底等高,
∴S△OAE=S△OBE ,
同理可证,S△OBF=S△OCF , S△ODG=S△OCG , S△ODH=S△OAH ,
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE ,
∵S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=7,
∴4+7=5+S四边形DHOG ,
解得,S四边形DHOG=6.
故答案为:6.
【分析】连接OC,OB,OA,OD,易证S△OBF=S△OCF , S△ODG=S△OCG , S△ODH=S△OAH , S△OAE=S△OBE , 所以S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE , 所以可以求出S四边形DHOG.
17、6;,,;,,;;;BC:CD:DE.
18.【答案】 解:∵点D、E分别是BC、AD边的中点,
∴S△ABD= S△ABC , S△ABE= S△ABD ,
∴S△ABE= S△ABC ,
∵S△ABC=1,
∴S△ABE=1× = .
【考点】三角形的角平分线、中线和高,三角形的面积
分析:根据三角形的中线平分三角形面积可得 S △ABE = S △ABC ,代入求解得出答案.
19【答案】 (1)解:如图,∠BED是△ABE的一个外角,
∵∠ABE=15°,∠BAD=55°,
∴∠BED=∠ABE+∠BAD
=15°+55°
=70°;
(2)解:∵AD是△ABC的中线,
∴S△ABD= S△ABC ,
又∵S△ABC=30,
∴S△ABD= ×30=15,
又∵BE为△ABD的中线,
∴S△BDE= S△ABD ,
∴S△BDE= ×15= ,
∵EF⊥BC,且EF=5
∴S△BDE = BD EF,
∴ BD×5= ,
∴BD=3,
∴CD=BD=3.
【考点】三角形的角平分线、中线和高,三角形的面积,三角形的外角性质
分析:(1)根据三角形内角与外角的性质解答即可;(2)根据三角形的中线将三角形分成两个三角形得到S△BDE= ,根据三角形面积公式求得CD=BD=3.
20【答案】 (1)解:①∵∠B=70°,∠C=30°,
∴∠BAC=180°-70°-30°=80°,
∵AE平分∠BAC,
∴∠BAE=40°;
②∵AD⊥BC,∠B=70°,
∴∠BAD=90°-∠B=90°-70°=20°,
而∠BAE=40°,
∴∠DAE=20°
(2)解:∵AE为角平分线,
∴∠BAE= (180°-∠B-∠C),
∵∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD= (180°-∠B-∠C)-(90°-∠B)= (∠B-∠C),
又∵∠B=∠C+40°,
∴∠B-∠C=40°,
∴∠DAE=20°.
【考点】三角形的角平分线、中线和高,三角形内角和定理
分析:(1)①利用三角形的内角和定理求出∠BAC,再利用角平分线定义求∠BAE.②先求出∠BAD,就可知道∠DAE的度数.(2)用∠B,∠C表示∠DAE,即可求岀∠DAE的度数.
21、如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.
【答案】(1)6.5;(2)1:4;(3)或.
【分析】
(1)根据中线的性质可知,点P在AB中点,CP把△ABC的面积分成相等的两部分,进而求解即可;
(2)求出当时,与的长,再根据等高的三角形面积比等于底边的比求解即可;
(3)分两种情况:①当P在AC上时;②当P在AB上时.
【详解】
(1)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时
∵点P在AB中点∴
∴CA+AP=12+7.5=19.5(cm),∴3t=19.5,解得t=6.5.
故当t=6.5时,CP把△ABC的面积分成相等的两部分;
(2)5×3=15,AP=15-12=3,BP=15-3=12,则S△APC:S△BPC=3:12=1:4;
(3)分两种情况:
①当P在AC上时,
∵△BCP的面积=18,∴×9×CP=18,∴CP=4,∴3t=4,∴t=;
②当P在AB上时,
∵△BCP的面积=18,△ABC面积=,
∴,∴3t=12+15×=22,解得t=.
故t=或秒时,△BCP的面积为18.
故答案为: 或.
(
1
)
一、选择题
1、小明作△ABC中AC边上的高线,下列三角板的摆放位置正确的是( )
A.B. C.D.
2.能将一个三角形分成面积相等的两个三角形的一条线段是( )
A. 三角形的高线 B. 边的中垂线 C. 三角形的中线 D. 三角形的角平分线
3.在下列各图的△ABC中,正确画出AC边上的高的图形是( )
A. B.
C. D.
4.下列说法错误的是( )
A. 任意三角形都有三条高线、中线、角平分线
B. 钝角三角形有两条高线在三角形的外部
C. 直角三角形只有一条高线
D. 锐角三角形的三条高线、三条中线、三条角平分线分别交于一点
5、袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
6.在中作边上的高,下列画法正确的是( )
A. B.
C. D.
7如图,AE是△ABC的角平分线,AD⊥BC于点D,点F为BC的中点,若∠BAC=104°,∠C=40°,则有下列结论:①∠BAE=52°;②∠DAE=2°;③EF=ED;④S△ABF= S△ABC.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
8.设△ABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……, 依此类推,则S5的值为( )
A. B. C. D.
二、填空题
9、如图所示,顶点是A、B、C的三角形,记作_______,读作___________ .
其中,顶点A所对的边为________还可用________表示;
顶点B所对的边为_______还可用________表示;
顶点C所对的边为___________还可用___________表示.
10、下列长度的三条线段:①5、6、12;②4、4、10;③4、6、10;④3、4、5.
能组成三角形的是______________.(填序号即可)
11.如图,已知是的中线,,,和的周长的差是__________.
12.如图,三边的中线、、相交于点若,则图中阴影部分的面积之和为 .
13.如图,在中,已知点为边上一点,、分别为边、的中点,且,则______.
14.△ABC中,AB=AC,一腰上的中线BD把三角形的周长分为9cm和12cm两部分,则此三角形的腰长是________.
15.如图,△ABC的面积为49cm2 , AE=ED,BD=3DC,则图中△AEF的面积等于________.
16.如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为4、5、7,四边形DHOG面积为________.
三、解答题
17、已知:如图,试回答下列问题:
(1)图中有_______个三角形,其中直角三角形是______.
(2)以线段AC为公共边的三角形是___________.
(3)线段CD所在的三角形是_______,BD边所对的角是________.
(4)、、这三个三角形的面积之比等于_______.
18.如图,在△ABC中,点D、E分别为BC、AD的中点,若S△ABC=1,求S△ABE .
19如图,AD为△ABC的中线,BE为△ABD的中线,过点E作EF垂直BC,垂足为点F.
(1)∠ABE=15 ,∠BAD=55 ,求∠BED的度数;
(2)若△ABC的面积为30,EF=5,求CD.
20如图,在△ABC中,AD⊥BC,AE平分∠BAC
(1)若∠B=70°,∠C=30°,求;
①∠BAE的度数.
②∠DAE的度数.
(2)探究:如果只知道∠B=∠C+40°,那么能求岀∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
21、如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.
1.D.
2.C.
3.C.
4.C.
5.D.
6.C
7.C
8.D
9、 三角形ABC BC a AC b AB c
10:④.
11.【答案】
12.【答案】
13.【答案】
14【答案】8cm或6cm
【考点】三角形三边关系
解:根据题意画出图形,如图,
设等腰三角形的腰长AB=AC=2x,BC=y,
∵BD是腰上的中线,
∴AD=DC=x,
若AB+AD的长为12,则2x+x=12,解得x=4cm,
则x+y=9,即4+y=9,解得y=5cm;
若AB+AD的长为9,则2x+x=9,解得x=3cm,
则x+y=12,即3+y=12,解得y=9cm;
所以等腰三角形的腰长为8cm或6cm.
故答案为:8cm或6cm.
【分析】由于本题没有说明把三角形分成两部分后哪部分长为9cm或12cm,所以需分情况说明,当AB+=9时,AB=6cm,因为三角形的周长为21cm,所以底边长为9cm,6+6>9,所以成立. 当时,AB=8cm,底边长为5cm,因为8+8>5,所以成立.
15.【答案】
【考点】三角形的面积
解:如图:
∵BD=3DC,△ABC的面积为49cm2 ,
∴S△ABD=S△ABC=cm2 , S△ADC=S△ABC=cm2,
∵AE=ED,
∴S△BED=S△ABD=cm2 , S△AEF=S△EFD ,
∴S△BDF=S△BED+S△AEF=+S△AEF ,
∵BD=3DC,
∴S△FDC=S△BDF=+S△AEF ,
∵S△ADC=S△AEF+S△EFD+S△FDC ,
∴=2S△AEF++S△AEF ,
∴S△AEF=cm2.
故答案为: .
【分析】连接DF,根据AE=ED,BD=3DC,及同高三角形的面积的关系得出S△AEF=S△EFD , S△ABE=S△BED , S△BDF=3S△FDC , S△ABD=3S△ADC , 根据△ABC的面积等于49cm2即可得出S△ABD=S△ABC=cm2 , S△ADC=S△ABC=cm2,S△BED=S△ABD=cm2 , S△BDF=S△BED+S△AEF=+S△AEF , S△FDC=S△BDF=+S△AEF , 最后根据S△ADC=S△AEF+S△EFD+S△FDC , 建立方程,求解即可.
16.【答案】 6
【考点】三角形的面积
解:连接OC,OB,OA,OD,
∵E、F、G、H依次是各边中点,
∴△AOE和△BOE等底等高,
∴S△OAE=S△OBE ,
同理可证,S△OBF=S△OCF , S△ODG=S△OCG , S△ODH=S△OAH ,
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE ,
∵S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=7,
∴4+7=5+S四边形DHOG ,
解得,S四边形DHOG=6.
故答案为:6.
【分析】连接OC,OB,OA,OD,易证S△OBF=S△OCF , S△ODG=S△OCG , S△ODH=S△OAH , S△OAE=S△OBE , 所以S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE , 所以可以求出S四边形DHOG.
17、6;,,;,,;;;BC:CD:DE.
18.【答案】 解:∵点D、E分别是BC、AD边的中点,
∴S△ABD= S△ABC , S△ABE= S△ABD ,
∴S△ABE= S△ABC ,
∵S△ABC=1,
∴S△ABE=1× = .
【考点】三角形的角平分线、中线和高,三角形的面积
分析:根据三角形的中线平分三角形面积可得 S △ABE = S △ABC ,代入求解得出答案.
19【答案】 (1)解:如图,∠BED是△ABE的一个外角,
∵∠ABE=15°,∠BAD=55°,
∴∠BED=∠ABE+∠BAD
=15°+55°
=70°;
(2)解:∵AD是△ABC的中线,
∴S△ABD= S△ABC ,
又∵S△ABC=30,
∴S△ABD= ×30=15,
又∵BE为△ABD的中线,
∴S△BDE= S△ABD ,
∴S△BDE= ×15= ,
∵EF⊥BC,且EF=5
∴S△BDE = BD EF,
∴ BD×5= ,
∴BD=3,
∴CD=BD=3.
【考点】三角形的角平分线、中线和高,三角形的面积,三角形的外角性质
分析:(1)根据三角形内角与外角的性质解答即可;(2)根据三角形的中线将三角形分成两个三角形得到S△BDE= ,根据三角形面积公式求得CD=BD=3.
20【答案】 (1)解:①∵∠B=70°,∠C=30°,
∴∠BAC=180°-70°-30°=80°,
∵AE平分∠BAC,
∴∠BAE=40°;
②∵AD⊥BC,∠B=70°,
∴∠BAD=90°-∠B=90°-70°=20°,
而∠BAE=40°,
∴∠DAE=20°
(2)解:∵AE为角平分线,
∴∠BAE= (180°-∠B-∠C),
∵∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD= (180°-∠B-∠C)-(90°-∠B)= (∠B-∠C),
又∵∠B=∠C+40°,
∴∠B-∠C=40°,
∴∠DAE=20°.
【考点】三角形的角平分线、中线和高,三角形内角和定理
分析:(1)①利用三角形的内角和定理求出∠BAC,再利用角平分线定义求∠BAE.②先求出∠BAD,就可知道∠DAE的度数.(2)用∠B,∠C表示∠DAE,即可求岀∠DAE的度数.
21、如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.
【答案】(1)6.5;(2)1:4;(3)或.
【分析】
(1)根据中线的性质可知,点P在AB中点,CP把△ABC的面积分成相等的两部分,进而求解即可;
(2)求出当时,与的长,再根据等高的三角形面积比等于底边的比求解即可;
(3)分两种情况:①当P在AC上时;②当P在AB上时.
【详解】
(1)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时
∵点P在AB中点∴
∴CA+AP=12+7.5=19.5(cm),∴3t=19.5,解得t=6.5.
故当t=6.5时,CP把△ABC的面积分成相等的两部分;
(2)5×3=15,AP=15-12=3,BP=15-3=12,则S△APC:S△BPC=3:12=1:4;
(3)分两种情况:
①当P在AC上时,
∵△BCP的面积=18,∴×9×CP=18,∴CP=4,∴3t=4,∴t=;
②当P在AB上时,
∵△BCP的面积=18,△ABC面积=,
∴,∴3t=12+15×=22,解得t=.
故t=或秒时,△BCP的面积为18.
故答案为: 或.
(
1
)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
