2021-2022学年华东师大版九年级数学下册第27章圆单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册第27章圆单元测试训练卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 460.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 01:00:27 | ||
图片预览


文档简介
华东师大版九年级数学下册
第27章 圆
单元测试训练卷
一、选择题(共10小题,4*10=40)
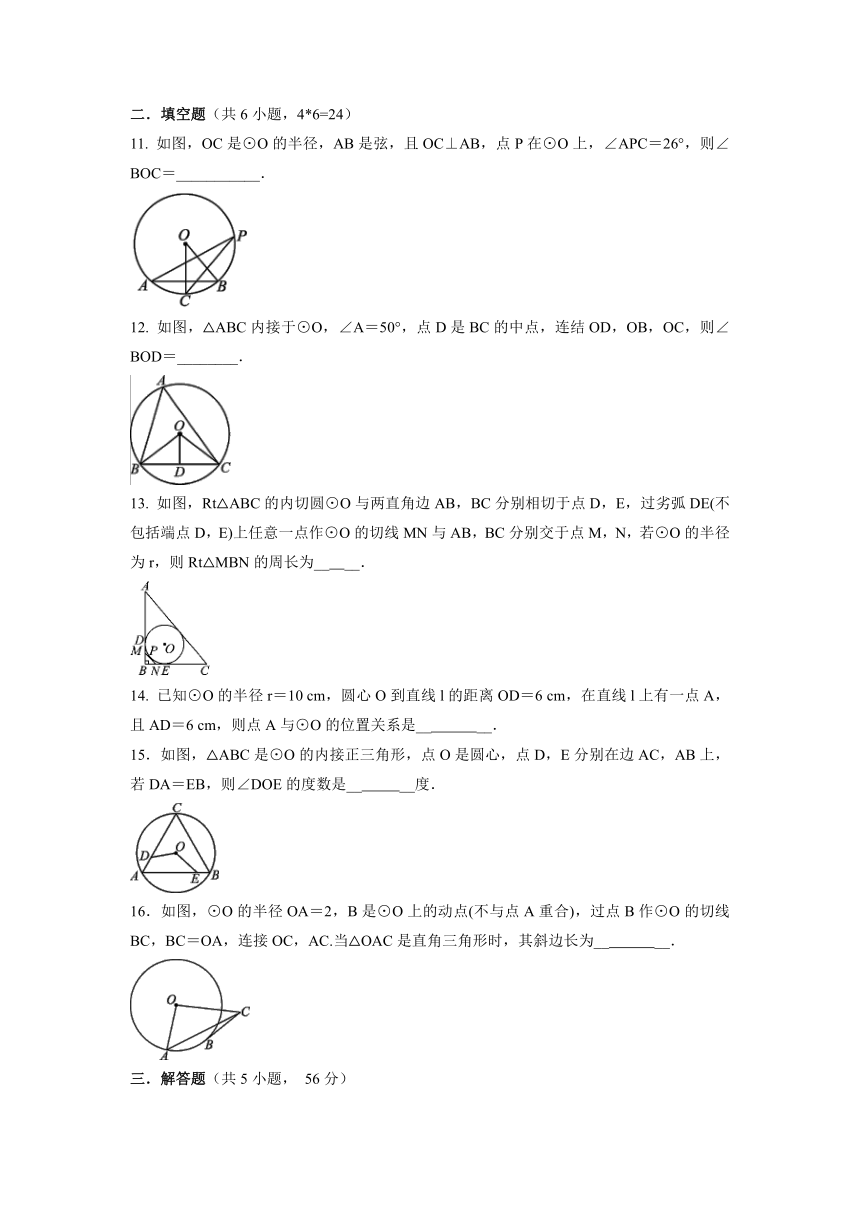
1. 如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数为( )
A.30° B.45° C.60° D.75°
2. 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD
C.= D.∠BCA=∠DCA
3. 在如图所示的网格图中,A、B、C、D、O均在格点上,则点O是( )
A.△ACD的内心 B.△ABC的内心
C.△ACD的外心 D.△ABC的外心
4. 如图,⊙O的直径AB垂直于弦CD,∠CAB=36°,则∠BCD的大小是( )
A.18° B.36° C.54° D.72°
5. 如图,正五边形ABCDE内接于⊙O,若⊙O的半径为5,则\s\up8(︵(︵)的长度为( )
A.π B.2π C.5π D.10π
6. ⊙O的半径为2,圆心O到直线l的距离为m,若m使得关于x的方程2x2-2x+m-1=0有实数根,则直线l与⊙O的位置关系为( )
A.相离或相切 B.相切或相交
C.相离或相交 D.无法确定
7. 如图,在四边形ABCD中,连结AC,BD,点O为AB的中点,若∠ADB=∠ACB=90°,则下面结论不一定正确的是( )
A.DC=CB B.∠DAC=∠DBC
C.∠BCD+∠BAD=180° D.点A,C,D到点O的距离相等
8. 若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )
A.60° B.90° C.120° D.180°
9.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A.- B.-2 C.π- D.-
10. 如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a?3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为4,则a的值是( )
A.4 B.3+ C.3 D.3+
二.填空题(共6小题,4*6=24)
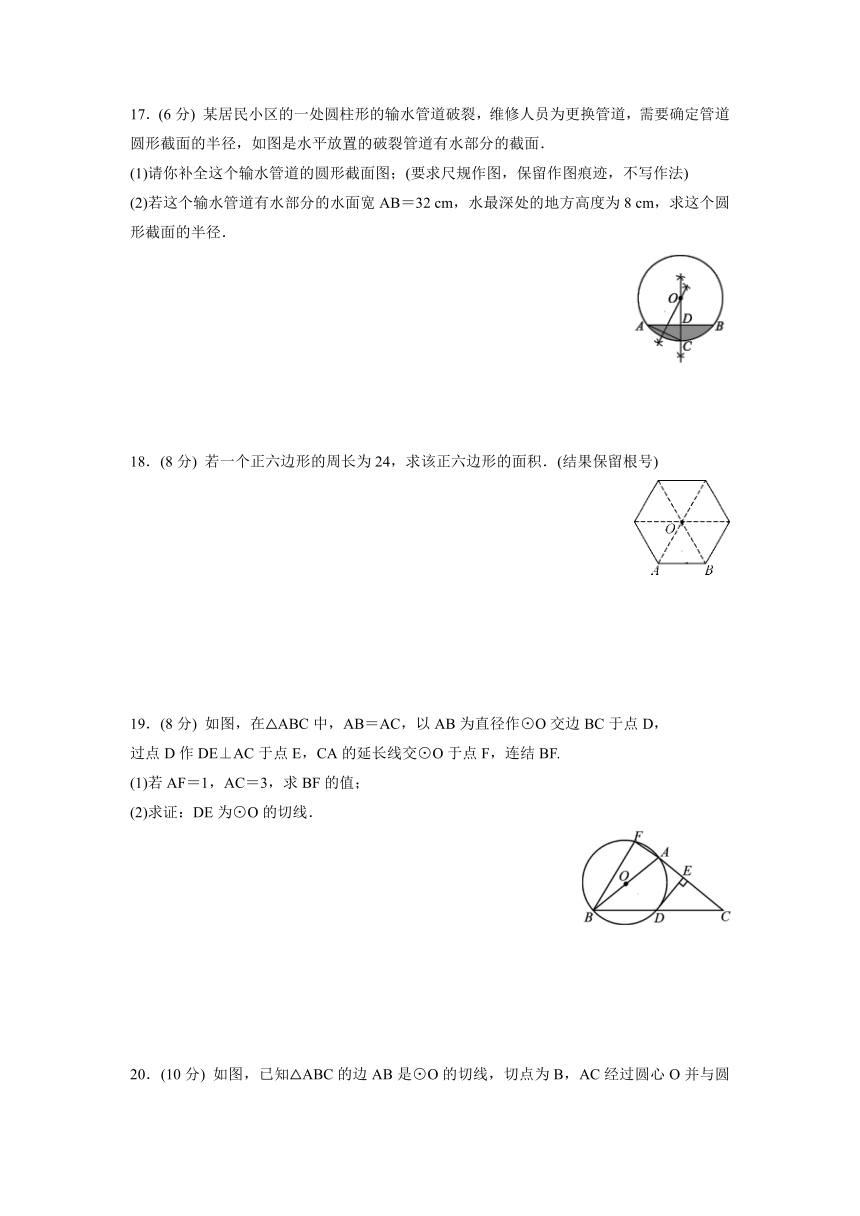
11. 如图,OC是⊙O的半径,AB是弦,且OC⊥AB,点P在⊙O上,∠APC=26°,则∠BOC=___________.
12. 如图,△ABC内接于⊙O,∠A=50°,点D是BC的中点,连结OD,OB,OC,则∠BOD=________.
13. 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任意一点作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为__ __.
14. 已知⊙O的半径r=10 cm,圆心O到直线l的距离OD=6 cm,在直线l上有一点A,且AD=6 cm,则点A与⊙O的位置关系是__ __.
15.如图,△ABC是⊙O的内接正三角形,点O是圆心,点D,E分别在边AC,AB上,若DA=EB,则∠DOE的度数是__ __度.
16.如图,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连接OC,AC.当△OAC是直角三角形时,其斜边长为__ __.
三.解答题(共5小题, 56分)
17.(6分) 某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面图;(要求尺规作图,保留作图痕迹,不写作法)
(2)若这个输水管道有水部分的水面宽AB=32 cm,水最深处的地方高度为8 cm,求这个圆形截面的半径.
18.(8分) 若一个正六边形的周长为24,求该正六边形的面积.(结果保留根号)
19.(8分) 如图,在△ABC中,AB=AC,以AB为直径作⊙O交边BC于点D,
过点D作DE⊥AC于点E,CA的延长线交⊙O于点F,连结BF.
(1)若AF=1,AC=3,求BF的值;
(2)求证:DE为⊙O的切线.
20.(10分) 如图,已知△ABC的边AB是⊙O的切线,切点为B,AC经过圆心O并与圆相交于点D、C,过点C作直线CE⊥AB,交AB的延长线于点E.
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
21.(12分) 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,恰有AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=2,OA=5,求⊙O的半径.
22.(12分) 如图,四边形ABCD为菱形,对角线AC、BD相交于点E,F是边BA的延长线上一点,连结EF,以EF为直径作⊙O,交DC于D、G两点,AD分别交EF、GF于I、H两点.
(1)试判断四边形FACD的形状,并证明你的结论;
(2)当G为线段DC的中点时,
①求证:FD=FI;
②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.
参考答案
1-5 CBDBB 6-10BACAB
11.52°
12.50°
13.2r
14.点A在⊙O内
15.120
16.2或2
17.解:(1)如图所示
(2)连结OA,作OC⊥AB于点D,并延长交⊙O于C,则D为AB的中点,∵AB=32 cm,∴AD=AB=16,设这个圆形截面的半径为x cm,又∵CD=8 cm,∴OD=x-8,在Rt△OAD中,∵OD2+AD2=OA2,即(x-8)2+162=x2,解得x=20,∴圆形截面的半径为20 cm
18.解:如图,过点O作OD⊥AB,垂足为点D.∵∠AOB=360°÷6=60°,OA=OB,∴△AOB为等边三角形,且三条对角线把正六边形分成了六个全等的等边三角形.∵正六边形的周长为24,∴AB=4.∵OD⊥AB,∴∠AOD=30°,AD=2.在Rt△AOD中,根据勾股定理得OD=2.∴S△AOB=×4×2=4.∴S正六边形=6×4=24.
19. 解:(1)∵AB为⊙O的直径,∴∠F=90°.∵AB=AC=3,AF=1,∴BF===2
(2)连结OD.∵AB=AC,OB=OD,∴∠ABC=∠C=∠ODB,∴OD∥AC.∵DE⊥AC,∴OD⊥DE,∴DE为⊙O的切线
20.(1)证明:连接OB.∵AB是⊙O的切线,∴OB⊥AB.又∵CE⊥AB,∴OB∥CE,∴∠OBC=∠BCE.∵OB=OC,∴∠OBC=∠OCB,∴∠BCE=∠OCB,∴CB平分∠ACE.
(2)解:连接BD.∵CD为⊙O的直径,∴∠CBD=90°,∴∠CBD=∠E.又∵∠DCB=∠BCE,∴△DBC∽△BEC,∴=.在Rt△BCE中,BC===5,∴=,即DC=,∴⊙O的半径是DC=.
21.(1)证明:如图,连接OB.∵OA⊥l,∴∠PAC=90°,∴∠APC+∠ACP=90°.∵AB=AC,OB=OP,∴∠ABC=∠ACB,∠OBP=∠OPB.∵∠BPO=∠APC,∴∠ABC+∠OBP=90°,即∠OBA=90°,∴OB⊥AB,∴AB是⊙O的切线.
(2)解:设⊙O的半径为r,则AP=5-r,OB=r.在Rt△OBA中,AB2=OA2-OB2=52-r2,在Rt△APC中,AC2=PC2-AP2=(2)2-(5-r)2.∵AB=AC,∴52-r2=(2)2-(5-r)2,解得r=3,即⊙O的半径为3.
22.解:(1)四边形FACD是平行四边形,理由如下:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴∠AEB=90°.又∵EF是⊙O的直径,∴∠FDE=90°,∴∠AEB=∠FDE,∴AC∥DF,∴四边形FACD是平行四边形.
(2)①证明:连结GE,∵四边形ABCD是菱形,∴点E为AC的中点.∵G为线段DC的中点,∴GE∥DA,∴∠FHI=∠FGE.∵FE是⊙O的直径,∴∠FGE=90°,∴∠FHI=90°.∵∠DEC=∠AEB=90°,G为线段DC的中点,∴DG=GE,∴=,∴∠1=∠2.∵∠1+∠3=90°,∠2+∠4=90°,∴∠3=∠4,∴FD=FI.
②∵AC∥DF,∴∠3=∠6.∵∠4=∠5,∠3=∠4,∴∠5=∠6,∴EI=EA.∵四边形ABCD是菱形,四边形FACD是平行四边形,∴DE=BD=n,AE=AC=m,FD=AC=2m,∴EF=FI+IE=FD+AE=3m.在Rt△EDF中,根据勾股定理可得n2+(2m)2=(3m)2,即n=m,∴S⊙O=π()2=πm2,S菱形ABCD=·2m·2n=2mn=2m2,∴S⊙O∶S菱形ABCD=9π∶40.
第27章 圆
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数为( )
A.30° B.45° C.60° D.75°
2. 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD
C.= D.∠BCA=∠DCA
3. 在如图所示的网格图中,A、B、C、D、O均在格点上,则点O是( )
A.△ACD的内心 B.△ABC的内心
C.△ACD的外心 D.△ABC的外心
4. 如图,⊙O的直径AB垂直于弦CD,∠CAB=36°,则∠BCD的大小是( )
A.18° B.36° C.54° D.72°
5. 如图,正五边形ABCDE内接于⊙O,若⊙O的半径为5,则\s\up8(︵(︵)的长度为( )
A.π B.2π C.5π D.10π
6. ⊙O的半径为2,圆心O到直线l的距离为m,若m使得关于x的方程2x2-2x+m-1=0有实数根,则直线l与⊙O的位置关系为( )
A.相离或相切 B.相切或相交
C.相离或相交 D.无法确定
7. 如图,在四边形ABCD中,连结AC,BD,点O为AB的中点,若∠ADB=∠ACB=90°,则下面结论不一定正确的是( )
A.DC=CB B.∠DAC=∠DBC
C.∠BCD+∠BAD=180° D.点A,C,D到点O的距离相等
8. 若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )
A.60° B.90° C.120° D.180°
9.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A.- B.-2 C.π- D.-
10. 如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a?3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为4,则a的值是( )
A.4 B.3+ C.3 D.3+
二.填空题(共6小题,4*6=24)
11. 如图,OC是⊙O的半径,AB是弦,且OC⊥AB,点P在⊙O上,∠APC=26°,则∠BOC=___________.
12. 如图,△ABC内接于⊙O,∠A=50°,点D是BC的中点,连结OD,OB,OC,则∠BOD=________.
13. 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任意一点作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为__ __.
14. 已知⊙O的半径r=10 cm,圆心O到直线l的距离OD=6 cm,在直线l上有一点A,且AD=6 cm,则点A与⊙O的位置关系是__ __.
15.如图,△ABC是⊙O的内接正三角形,点O是圆心,点D,E分别在边AC,AB上,若DA=EB,则∠DOE的度数是__ __度.
16.如图,⊙O的半径OA=2,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连接OC,AC.当△OAC是直角三角形时,其斜边长为__ __.
三.解答题(共5小题, 56分)
17.(6分) 某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面图;(要求尺规作图,保留作图痕迹,不写作法)
(2)若这个输水管道有水部分的水面宽AB=32 cm,水最深处的地方高度为8 cm,求这个圆形截面的半径.
18.(8分) 若一个正六边形的周长为24,求该正六边形的面积.(结果保留根号)
19.(8分) 如图,在△ABC中,AB=AC,以AB为直径作⊙O交边BC于点D,
过点D作DE⊥AC于点E,CA的延长线交⊙O于点F,连结BF.
(1)若AF=1,AC=3,求BF的值;
(2)求证:DE为⊙O的切线.
20.(10分) 如图,已知△ABC的边AB是⊙O的切线,切点为B,AC经过圆心O并与圆相交于点D、C,过点C作直线CE⊥AB,交AB的延长线于点E.
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
21.(12分) 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,恰有AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=2,OA=5,求⊙O的半径.
22.(12分) 如图,四边形ABCD为菱形,对角线AC、BD相交于点E,F是边BA的延长线上一点,连结EF,以EF为直径作⊙O,交DC于D、G两点,AD分别交EF、GF于I、H两点.
(1)试判断四边形FACD的形状,并证明你的结论;
(2)当G为线段DC的中点时,
①求证:FD=FI;
②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.
参考答案
1-5 CBDBB 6-10BACAB
11.52°
12.50°
13.2r
14.点A在⊙O内
15.120
16.2或2
17.解:(1)如图所示
(2)连结OA,作OC⊥AB于点D,并延长交⊙O于C,则D为AB的中点,∵AB=32 cm,∴AD=AB=16,设这个圆形截面的半径为x cm,又∵CD=8 cm,∴OD=x-8,在Rt△OAD中,∵OD2+AD2=OA2,即(x-8)2+162=x2,解得x=20,∴圆形截面的半径为20 cm
18.解:如图,过点O作OD⊥AB,垂足为点D.∵∠AOB=360°÷6=60°,OA=OB,∴△AOB为等边三角形,且三条对角线把正六边形分成了六个全等的等边三角形.∵正六边形的周长为24,∴AB=4.∵OD⊥AB,∴∠AOD=30°,AD=2.在Rt△AOD中,根据勾股定理得OD=2.∴S△AOB=×4×2=4.∴S正六边形=6×4=24.
19. 解:(1)∵AB为⊙O的直径,∴∠F=90°.∵AB=AC=3,AF=1,∴BF===2
(2)连结OD.∵AB=AC,OB=OD,∴∠ABC=∠C=∠ODB,∴OD∥AC.∵DE⊥AC,∴OD⊥DE,∴DE为⊙O的切线
20.(1)证明:连接OB.∵AB是⊙O的切线,∴OB⊥AB.又∵CE⊥AB,∴OB∥CE,∴∠OBC=∠BCE.∵OB=OC,∴∠OBC=∠OCB,∴∠BCE=∠OCB,∴CB平分∠ACE.
(2)解:连接BD.∵CD为⊙O的直径,∴∠CBD=90°,∴∠CBD=∠E.又∵∠DCB=∠BCE,∴△DBC∽△BEC,∴=.在Rt△BCE中,BC===5,∴=,即DC=,∴⊙O的半径是DC=.
21.(1)证明:如图,连接OB.∵OA⊥l,∴∠PAC=90°,∴∠APC+∠ACP=90°.∵AB=AC,OB=OP,∴∠ABC=∠ACB,∠OBP=∠OPB.∵∠BPO=∠APC,∴∠ABC+∠OBP=90°,即∠OBA=90°,∴OB⊥AB,∴AB是⊙O的切线.
(2)解:设⊙O的半径为r,则AP=5-r,OB=r.在Rt△OBA中,AB2=OA2-OB2=52-r2,在Rt△APC中,AC2=PC2-AP2=(2)2-(5-r)2.∵AB=AC,∴52-r2=(2)2-(5-r)2,解得r=3,即⊙O的半径为3.
22.解:(1)四边形FACD是平行四边形,理由如下:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴∠AEB=90°.又∵EF是⊙O的直径,∴∠FDE=90°,∴∠AEB=∠FDE,∴AC∥DF,∴四边形FACD是平行四边形.
(2)①证明:连结GE,∵四边形ABCD是菱形,∴点E为AC的中点.∵G为线段DC的中点,∴GE∥DA,∴∠FHI=∠FGE.∵FE是⊙O的直径,∴∠FGE=90°,∴∠FHI=90°.∵∠DEC=∠AEB=90°,G为线段DC的中点,∴DG=GE,∴=,∴∠1=∠2.∵∠1+∠3=90°,∠2+∠4=90°,∴∠3=∠4,∴FD=FI.
②∵AC∥DF,∴∠3=∠6.∵∠4=∠5,∠3=∠4,∴∠5=∠6,∴EI=EA.∵四边形ABCD是菱形,四边形FACD是平行四边形,∴DE=BD=n,AE=AC=m,FD=AC=2m,∴EF=FI+IE=FD+AE=3m.在Rt△EDF中,根据勾股定理可得n2+(2m)2=(3m)2,即n=m,∴S⊙O=π()2=πm2,S菱形ABCD=·2m·2n=2mn=2m2,∴S⊙O∶S菱形ABCD=9π∶40.
