激活思维的数学教学——从命题考查意图谈日常数学教学
文档属性
| 名称 | 激活思维的数学教学——从命题考查意图谈日常数学教学 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-29 00:00:00 | ||
图片预览








文档简介
课件71张PPT。激活思维的数学教学——从命题考查意图谈日常数学教学试题是怎么出的?从定义
从定理
从例题
从习题
从试题
从听课
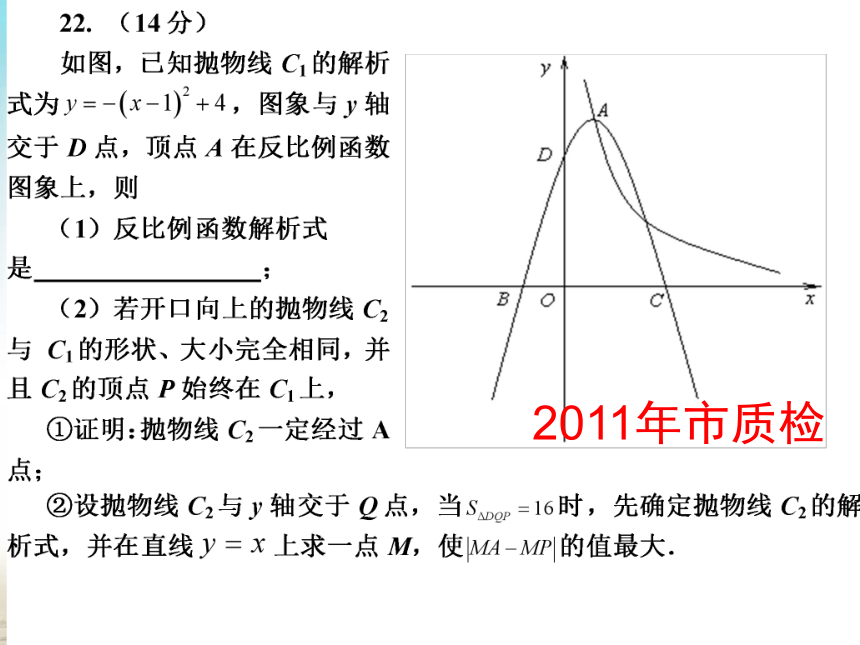
从交流找出题目的家谱1.二次函数y=x2图象的顶点坐标是( ) A.(0,0) B.(1,1) C.(1,0) D.(0,1) 1.顶点是(0,0)的二次函数解析式是?
2.顶点是(1,1)的二次函数解析式是?
3.顶点是(1,0)的二次函数解析式是?
4.顶点是(0,1)的二次函数解析式是?
5.顶点在x轴上的二次函数解析式是?
6.顶点在y轴上的二次函数解析式是?
7.顶点在一、三象限角平分线上的二次函数解析式是?
8.顶点在二、四象限角平分线上的二次函数解析式是?
9.顶点在直线y=kx上的二次函数解析式是?
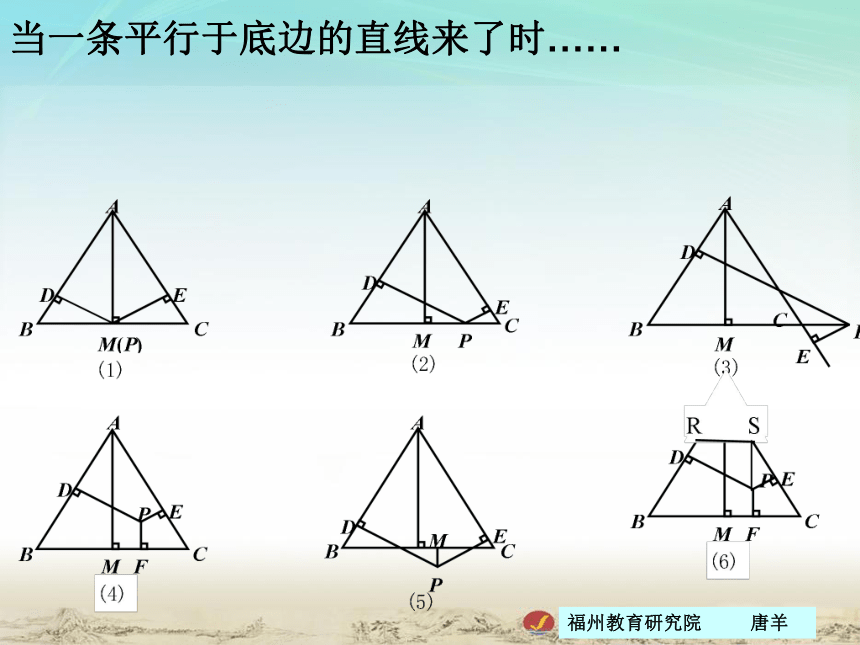
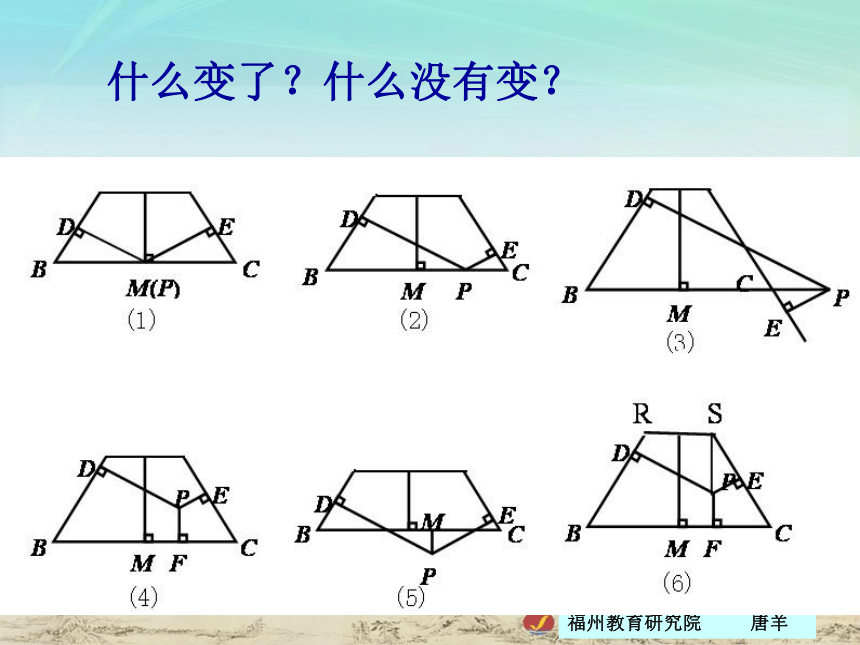
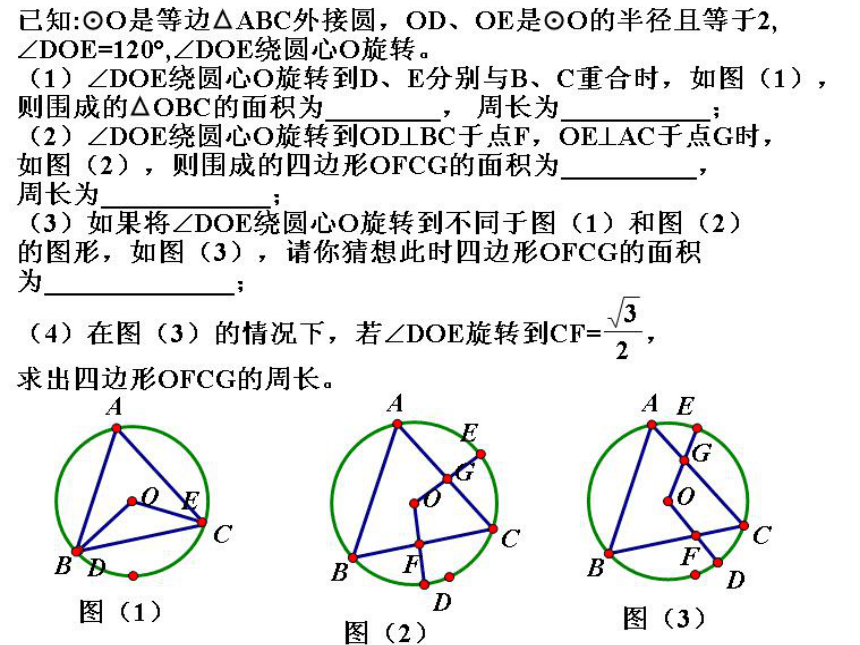
10.顶点在双曲线 上的二次函数解析式是? 上述变式源于课本中的小贴士2011年市质检2011年中考压轴题当一条平行于底边的直线来了时……什么变了?什么没有变?总结提升: 无论∠DOE绕圆心O怎样转动, ∠DOE的两边与
△ABC的两边相交,所围成的图形的面积不变,都
等于 S△ABC,周长为AC+2OG;当OG取最小值时,周
长最小,最小值为2 +2.问题思考: 若将上面问题中的等边三角形换成正方形,探究得到的
结论还成立吗?若不成立,应改变什么条件后可以继续探
究得出类似的结论.技能大赛培训中的一题94年高考题在测量某物理量的过程中,因仪器和观察的误差,使得n次测量分别得到 共n个数据。我们规定所测量的“最佳近视值”a是这样一个量:与其他近似值比较,a与
各数据的差的平方和最小,依次规定,从
推出a=____________________; 期末考试范围——到二次函数关注:
运算能力、
代数式的化简及结构特征、
二次方程求根公式、二次函数顶点式的推导过程、
从函数的观点看方程与不等式、
对课本例习题的变式应用
教师对教材的研读(激活思维)考查意图学生方面:
数学文字的阅读理解能力
数学语言的表达能力
图形识别能力
运算与化简能力
教师方面:
兴趣、思维、习惯……
让学生读懂数学文字与数学图形关于规范化要求何时咬文嚼字——概念、公式、定理
——尺规作图、作图语言
——例题的示范性解答画圆、作角平分线尺规作图——目的是严谨的作图几何语言
用替代品——目的是强调本质属性,为什么可以替代?
只有尺没有规——合理的数学推理
没有尺也没有规——考验你的想像力和应变力
替代的合理性思考——这是我们要教给学生的新课标要求降低难度,
提高要求。
知识的上限,
能力的下限。课标的三个基本要求 激发兴趣
引发思考
培养习惯如何理解平方根、立方根概念?它与方根的区别与联系?听课调研中发现的问题脱离课本资源的经验之谈
取舍、定位、实施、反馈、思考、修正
体罚式的计算训练
一行的专注
“念念不舍”——拖课现象
瘦身、骨感——核心、主线
来无踪去无影——知识的横空出世
上下五千年,纵横八万里学生是怎么做的?学生是怎么想的?解方程公式法解方程配方第二次修正为什么会一错再错?有等根的方程
B.x2+2x-1=0
D.4x2-4x+1=0从模仿走向有思考的学习!b2-4ac何以成为根的判别式?
一个方程有根或无(实数)根,究竟由谁来决定?
建议:将一元二次方程的求根公式认真推导一遍(想一想每一步的理由?根据?)然后再对照着推导二次函数的顶点式。二次函数中对数与式的要求P2
P5
P14第7题
P15
P17
P19
P30
144分的学生怎么错的
2.x取何值时,下列各式有意义
(1) (2) (3)(4)题不在多,不在难而在于让大家
明白、明理、明智!有人说:“世界上两件事最难:
一是把自己的思想装进别人的脑袋,
二是把别人的钱装进自己的口袋。?!半期考试题选析4.把一个正五角星绕着中心旋转到与原来重合,至少需要转动的度数是( )
A.36° B.72° C.108° D.144°
为何得分低?为何多选C?12.请你写出一个有一根为1的一元二次方程: .有一根为1的一元二次方程有何特征?8.如图,量角器外缘上有A、B两点,它们所表示的读数分别是80°、50°,则∠ACB应为( ) A.25° B.15° C.30° D.50°7.在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )
A.12 B.9
C.4 D.35.图中圆与圆之间不同的位置关系有( ) A.2种 B.3种 C.4种 D.5种 还可以怎么考?6.下列关于x的一元二次方程中,有两个相等的实数根的方程是( )
A.x2+4=0 B.x2+2x-1=0 C.x2+x+3=0 D.4x2-4x+1=0换一种方式思考7.在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )
A.12 B.9 C.4 D.313.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=6cm,则此光盘的直径是_____cm.第13题【一万小时定律】一个人的技能要达到大师级水平,工作时间必须超过1万小时——任何行业都不能例外:莫扎特6岁作曲,到20岁才创作世界级作品;甲壳虫乐队1964年风靡全球前已演出1200场;微软创始人比尔盖茨1968年接触计算机,创业前已编程7年。你能在自己的工作上坚持10年甚至以上吗?期待大师级的你! 放开,我就看看,我不碰……
想像一下这会是怎样的情境……
还有其他的可能吗?求边长分别为300、400的三角形第三边上的高。
你希望它是什么三角形?为什么 ?
你希望它的第三边多长?为什么?
当没有出现你所希望的值时怎么办?
如何确定它是可解的?激起学生思维的兴奋点二次函数y=a(x-h)2的图像与性质闽侯六中 高巧燕温故知新向上向下(0 ,0)(0 ,0)直线x=0即y轴当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。 当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。 x=0时,y最小=0x=0时,y最大=0抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来, |a|越大,抛物线的开口就越小.
直线x=0即y轴把二次函数 的图象E向左平移1个单位,得到图形F,如图.EFO'探究由于平移不改变图形的形状和大小,因此在向左平移1个单位后;图形F也是抛物线F的顶点O,(-1, 0)F的对称轴:直线X=-1F也开口向上在抛物线 上任取一点 ,它在向左平移1个单位后,P的对称点Q的坐标是什么?把点P的横坐标a减去1,纵坐标
不变,即对称点Q的坐标为抛物线F是哪个函数的图象呢?这样我们证明了:函数 的图象是抛物线F。它的顶点是O'(-1,0),它的对称轴是直线x =-1,抛物线的开口向上.
这表明:点Q在函数 的图象上,由此得出,抛物线F是函数 的图象,证 明:记x=a-1,则a=x+1,从而点Q的坐标为类似地,我们可以证明得到下述结论:函数y=a(x-h)2的图像是一条抛物线,对称轴是直线x=h,顶点坐标
(h,0),当 a>0时,抛物线开口向上;当a<0时,抛物线开口向下由于我们已经知道了函数 y=a(x-h)2 的图象的性质,因此今后在画y=a(x-h)2 的图象,只要先画出对称轴以及图象在对称轴右边的部分,然后利用对称性,画出左边的部分,在画图象的右边部分时,只需要“列表,描点,连线”三个步骤就可以了.
画函数 的图象.解 抛物线 的对称轴是 直线x=2,顶点坐标是(2,0)列表:自变量x从顶点的横坐标2开始取值.描点和连线:画出图象在对称轴右边的部分.例题:利用对称性画出图象在对称轴左边的部分:这样我们得到了函数 的图象 . 1.画二次函数 的图象X=1例题:说出下列二次函数图象的开口方向,对称轴,顶点坐标,极值和增减性对称轴 :直线 x=5顶点坐标(5,0)对称轴 :直线 x=-2顶点坐标(-2,0)解:解:抛物线开口向上当 x=5时,y有最小值为0当x<5时,y随x的增大而减小
当x>5时,y随x的增大而增大抛物线开口向下当x=-2时,y有最大值为0当x<-2时,y 随x的增大而增大
当x>-2时,y随x的增大而减小填空向下
向下向上向下直线x=-2直线x=2(-2,0)当x=-2时
最大值y=0(2,0)当x=2时
最小值y=0直线x=0即y轴(0,-1)当x=0时
最大值y=-1直线x=0即y轴
(0,1)当 x=0时
最大值y=1(1)抛物线y=2x2向左平移1个单位得到抛物线y=2(x+1)2(2)抛物线y=2x2向右平移2个单位得到抛物线y=2(x-2)2(3)抛物线y=2(x-2)2向左平移2个单位得到抛物线y=2x2(4)抛物线y=2(x-1)2向右平移2个单位得到抛物线y=2(x-3)2(7)抛物线y=2(x+1)2向左平移3个单位后再向下平移1个单位得到抛物线y=2(x+4)2-1(6)小明在白纸上画了直角坐标系,然后把透明纸覆盖在白纸上,在透明纸
上描出了抛物线y=-2(x-3)2,欣赏时不小心把画有坐标系的白纸向右移动了
1个单位,这时透明纸上的抛物线的解析式是y=-2(x-2)2大显身手(5)抛物线向右平移1个单位后得到抛物线y=3(x+2)2,则原抛物线
解析式是y=3(x+3)2小结抛物线y=ax2, y=ax2+k, y=a(x-h)2之间的关系a>0,向上
a<0,向下a>0,向上
a<0,向下a>0,向上
a<0,向下直线x=0
即y轴直线x=0
即y轴
直线x=h(0,0)(0,k)(h,0)a>0,最小值y=0a<0,最大值y=0a>0,最小值y=ka<0,最大值y=ka>0,最小值y=0a<0,最大值y=0y=ax2
上下平移
得到
y=ax2+ky=ax2
左右平移
得到
y=a(x-h)2良好的学习习惯阅读的习惯;
动手的习惯;
思考的习惯;
表达的习惯;
整理、归纳的习惯;
教师生活的理想状态宁静地沉思
执着地追问
潜心地创造
从容地生活
————程光泉(北师大教授)谢谢!
从定理
从例题
从习题
从试题
从听课
从交流找出题目的家谱1.二次函数y=x2图象的顶点坐标是( ) A.(0,0) B.(1,1) C.(1,0) D.(0,1) 1.顶点是(0,0)的二次函数解析式是?
2.顶点是(1,1)的二次函数解析式是?
3.顶点是(1,0)的二次函数解析式是?
4.顶点是(0,1)的二次函数解析式是?
5.顶点在x轴上的二次函数解析式是?
6.顶点在y轴上的二次函数解析式是?
7.顶点在一、三象限角平分线上的二次函数解析式是?
8.顶点在二、四象限角平分线上的二次函数解析式是?
9.顶点在直线y=kx上的二次函数解析式是?
10.顶点在双曲线 上的二次函数解析式是? 上述变式源于课本中的小贴士2011年市质检2011年中考压轴题当一条平行于底边的直线来了时……什么变了?什么没有变?总结提升: 无论∠DOE绕圆心O怎样转动, ∠DOE的两边与
△ABC的两边相交,所围成的图形的面积不变,都
等于 S△ABC,周长为AC+2OG;当OG取最小值时,周
长最小,最小值为2 +2.问题思考: 若将上面问题中的等边三角形换成正方形,探究得到的
结论还成立吗?若不成立,应改变什么条件后可以继续探
究得出类似的结论.技能大赛培训中的一题94年高考题在测量某物理量的过程中,因仪器和观察的误差,使得n次测量分别得到 共n个数据。我们规定所测量的“最佳近视值”a是这样一个量:与其他近似值比较,a与
各数据的差的平方和最小,依次规定,从
推出a=____________________; 期末考试范围——到二次函数关注:
运算能力、
代数式的化简及结构特征、
二次方程求根公式、二次函数顶点式的推导过程、
从函数的观点看方程与不等式、
对课本例习题的变式应用
教师对教材的研读(激活思维)考查意图学生方面:
数学文字的阅读理解能力
数学语言的表达能力
图形识别能力
运算与化简能力
教师方面:
兴趣、思维、习惯……
让学生读懂数学文字与数学图形关于规范化要求何时咬文嚼字——概念、公式、定理
——尺规作图、作图语言
——例题的示范性解答画圆、作角平分线尺规作图——目的是严谨的作图几何语言
用替代品——目的是强调本质属性,为什么可以替代?
只有尺没有规——合理的数学推理
没有尺也没有规——考验你的想像力和应变力
替代的合理性思考——这是我们要教给学生的新课标要求降低难度,
提高要求。
知识的上限,
能力的下限。课标的三个基本要求 激发兴趣
引发思考
培养习惯如何理解平方根、立方根概念?它与方根的区别与联系?听课调研中发现的问题脱离课本资源的经验之谈
取舍、定位、实施、反馈、思考、修正
体罚式的计算训练
一行的专注
“念念不舍”——拖课现象
瘦身、骨感——核心、主线
来无踪去无影——知识的横空出世
上下五千年,纵横八万里学生是怎么做的?学生是怎么想的?解方程公式法解方程配方第二次修正为什么会一错再错?有等根的方程
B.x2+2x-1=0
D.4x2-4x+1=0从模仿走向有思考的学习!b2-4ac何以成为根的判别式?
一个方程有根或无(实数)根,究竟由谁来决定?
建议:将一元二次方程的求根公式认真推导一遍(想一想每一步的理由?根据?)然后再对照着推导二次函数的顶点式。二次函数中对数与式的要求P2
P5
P14第7题
P15
P17
P19
P30
144分的学生怎么错的
2.x取何值时,下列各式有意义
(1) (2) (3)(4)题不在多,不在难而在于让大家
明白、明理、明智!有人说:“世界上两件事最难:
一是把自己的思想装进别人的脑袋,
二是把别人的钱装进自己的口袋。?!半期考试题选析4.把一个正五角星绕着中心旋转到与原来重合,至少需要转动的度数是( )
A.36° B.72° C.108° D.144°
为何得分低?为何多选C?12.请你写出一个有一根为1的一元二次方程: .有一根为1的一元二次方程有何特征?8.如图,量角器外缘上有A、B两点,它们所表示的读数分别是80°、50°,则∠ACB应为( ) A.25° B.15° C.30° D.50°7.在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )
A.12 B.9
C.4 D.35.图中圆与圆之间不同的位置关系有( ) A.2种 B.3种 C.4种 D.5种 还可以怎么考?6.下列关于x的一元二次方程中,有两个相等的实数根的方程是( )
A.x2+4=0 B.x2+2x-1=0 C.x2+x+3=0 D.4x2-4x+1=0换一种方式思考7.在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )
A.12 B.9 C.4 D.313.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=6cm,则此光盘的直径是_____cm.第13题【一万小时定律】一个人的技能要达到大师级水平,工作时间必须超过1万小时——任何行业都不能例外:莫扎特6岁作曲,到20岁才创作世界级作品;甲壳虫乐队1964年风靡全球前已演出1200场;微软创始人比尔盖茨1968年接触计算机,创业前已编程7年。你能在自己的工作上坚持10年甚至以上吗?期待大师级的你! 放开,我就看看,我不碰……
想像一下这会是怎样的情境……
还有其他的可能吗?求边长分别为300、400的三角形第三边上的高。
你希望它是什么三角形?为什么 ?
你希望它的第三边多长?为什么?
当没有出现你所希望的值时怎么办?
如何确定它是可解的?激起学生思维的兴奋点二次函数y=a(x-h)2的图像与性质闽侯六中 高巧燕温故知新向上向下(0 ,0)(0 ,0)直线x=0即y轴当x<0时,
y随着x的增大而减小。
当x>0时,
y随着x的增大而增大。 当x<0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。 x=0时,y最小=0x=0时,y最大=0抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来, |a|越大,抛物线的开口就越小.
直线x=0即y轴把二次函数 的图象E向左平移1个单位,得到图形F,如图.EFO'探究由于平移不改变图形的形状和大小,因此在向左平移1个单位后;图形F也是抛物线F的顶点O,(-1, 0)F的对称轴:直线X=-1F也开口向上在抛物线 上任取一点 ,它在向左平移1个单位后,P的对称点Q的坐标是什么?把点P的横坐标a减去1,纵坐标
不变,即对称点Q的坐标为抛物线F是哪个函数的图象呢?这样我们证明了:函数 的图象是抛物线F。它的顶点是O'(-1,0),它的对称轴是直线x =-1,抛物线的开口向上.
这表明:点Q在函数 的图象上,由此得出,抛物线F是函数 的图象,证 明:记x=a-1,则a=x+1,从而点Q的坐标为类似地,我们可以证明得到下述结论:函数y=a(x-h)2的图像是一条抛物线,对称轴是直线x=h,顶点坐标
(h,0),当 a>0时,抛物线开口向上;当a<0时,抛物线开口向下由于我们已经知道了函数 y=a(x-h)2 的图象的性质,因此今后在画y=a(x-h)2 的图象,只要先画出对称轴以及图象在对称轴右边的部分,然后利用对称性,画出左边的部分,在画图象的右边部分时,只需要“列表,描点,连线”三个步骤就可以了.
画函数 的图象.解 抛物线 的对称轴是 直线x=2,顶点坐标是(2,0)列表:自变量x从顶点的横坐标2开始取值.描点和连线:画出图象在对称轴右边的部分.例题:利用对称性画出图象在对称轴左边的部分:这样我们得到了函数 的图象 . 1.画二次函数 的图象X=1例题:说出下列二次函数图象的开口方向,对称轴,顶点坐标,极值和增减性对称轴 :直线 x=5顶点坐标(5,0)对称轴 :直线 x=-2顶点坐标(-2,0)解:解:抛物线开口向上当 x=5时,y有最小值为0当x<5时,y随x的增大而减小
当x>5时,y随x的增大而增大抛物线开口向下当x=-2时,y有最大值为0当x<-2时,y 随x的增大而增大
当x>-2时,y随x的增大而减小填空向下
向下向上向下直线x=-2直线x=2(-2,0)当x=-2时
最大值y=0(2,0)当x=2时
最小值y=0直线x=0即y轴(0,-1)当x=0时
最大值y=-1直线x=0即y轴
(0,1)当 x=0时
最大值y=1(1)抛物线y=2x2向左平移1个单位得到抛物线y=2(x+1)2(2)抛物线y=2x2向右平移2个单位得到抛物线y=2(x-2)2(3)抛物线y=2(x-2)2向左平移2个单位得到抛物线y=2x2(4)抛物线y=2(x-1)2向右平移2个单位得到抛物线y=2(x-3)2(7)抛物线y=2(x+1)2向左平移3个单位后再向下平移1个单位得到抛物线y=2(x+4)2-1(6)小明在白纸上画了直角坐标系,然后把透明纸覆盖在白纸上,在透明纸
上描出了抛物线y=-2(x-3)2,欣赏时不小心把画有坐标系的白纸向右移动了
1个单位,这时透明纸上的抛物线的解析式是y=-2(x-2)2大显身手(5)抛物线向右平移1个单位后得到抛物线y=3(x+2)2,则原抛物线
解析式是y=3(x+3)2小结抛物线y=ax2, y=ax2+k, y=a(x-h)2之间的关系a>0,向上
a<0,向下a>0,向上
a<0,向下a>0,向上
a<0,向下直线x=0
即y轴直线x=0
即y轴
直线x=h(0,0)(0,k)(h,0)a>0,最小值y=0a<0,最大值y=0a>0,最小值y=ka<0,最大值y=ka>0,最小值y=0a<0,最大值y=0y=ax2
上下平移
得到
y=ax2+ky=ax2
左右平移
得到
y=a(x-h)2良好的学习习惯阅读的习惯;
动手的习惯;
思考的习惯;
表达的习惯;
整理、归纳的习惯;
教师生活的理想状态宁静地沉思
执着地追问
潜心地创造
从容地生活
————程光泉(北师大教授)谢谢!
同课章节目录
