2021-2022学年人教版(五四制)数学九年级下册第33章相似单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版(五四制)数学九年级下册第33章相似单元测试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 351.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教五四新版九年级下册数学《第33章 相似》单元测试卷
一.选择题
1.若,则的值等于( )
A. B. C. D.
2.已知3x=5y(y≠0),则下列比例式成立的是( )
A.= B.= C.= D.=
3.下列各组的四条线段a,b,c,d是成比例线段的是( )
A.a=4,b=6,c=5,d=10 B.a=1,b=2,c=3,d=4
C.,b=3,c=2, D.a=2,,,
4.下列判断正确的是( )
A.所有等腰三角形都相似 B.所有直角三角形都相似
C.所有菱形都相似 D.所有等边三角形都相似
5.若=,则的值是( )
A.3 B. C. D.2
6.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠H等于( )
A.70° B.80° C.110° D.120°
7.若两个相似多边形的面积比为25:36,则它们的对应边的比是( )
A.5:6 B.6:5 C.25:36 D.36:25
8.如图,点B在线段AC上,且,设AC=2,则AB的长为( )
A. B. C. D.
9.如图所示,△ABC∽△DEF,则∠D的度数为( )
A.35° B.45° C.65° D.80°
10.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,若,则的值为( )
A. B. C. D.
二.填空题
11.四边形ABCD∽四边形A′B′C′D′,∠A=70°,∠B′=108°,∠C′=92°,则∠D= 度.
12.如图,在三角形ABC中,AB=24,AC=18,D是AC上一点AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE= .
13.如图所示,已知在梯形ABCD中,AD∥BC,=,则= .
14.如果,那么= .
15.已知,则= .
16.若=,则的值等于 .
17.已知线段a=4,b=8,则a、b的比例中项线段等于 .
18.若点P是线段AB的黄金分割点,且AP>BP,AB=2,则AP= .(保留根号)
19.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
20.如图所示的正方形网格中,每个小正方形的边长均为1,四边形ABCD的面积是 .若四边形EFGH与四边形ABCD相似,则四边形EFGH的面积是 .
三.解答题
21.如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度.
22.已知==,且3a﹣2b+c=9,求2a+4b﹣3c的值.
23.已知==,且a+b+c=68.求a、b、c的值.
24.如图,已知线段AB上有两点M,N,满足AM:MB=5:11,AN:NB=5:7,NM=1.5,求AB的长.
25.已知a:b=3:2,求:
(1);
(2)的值.
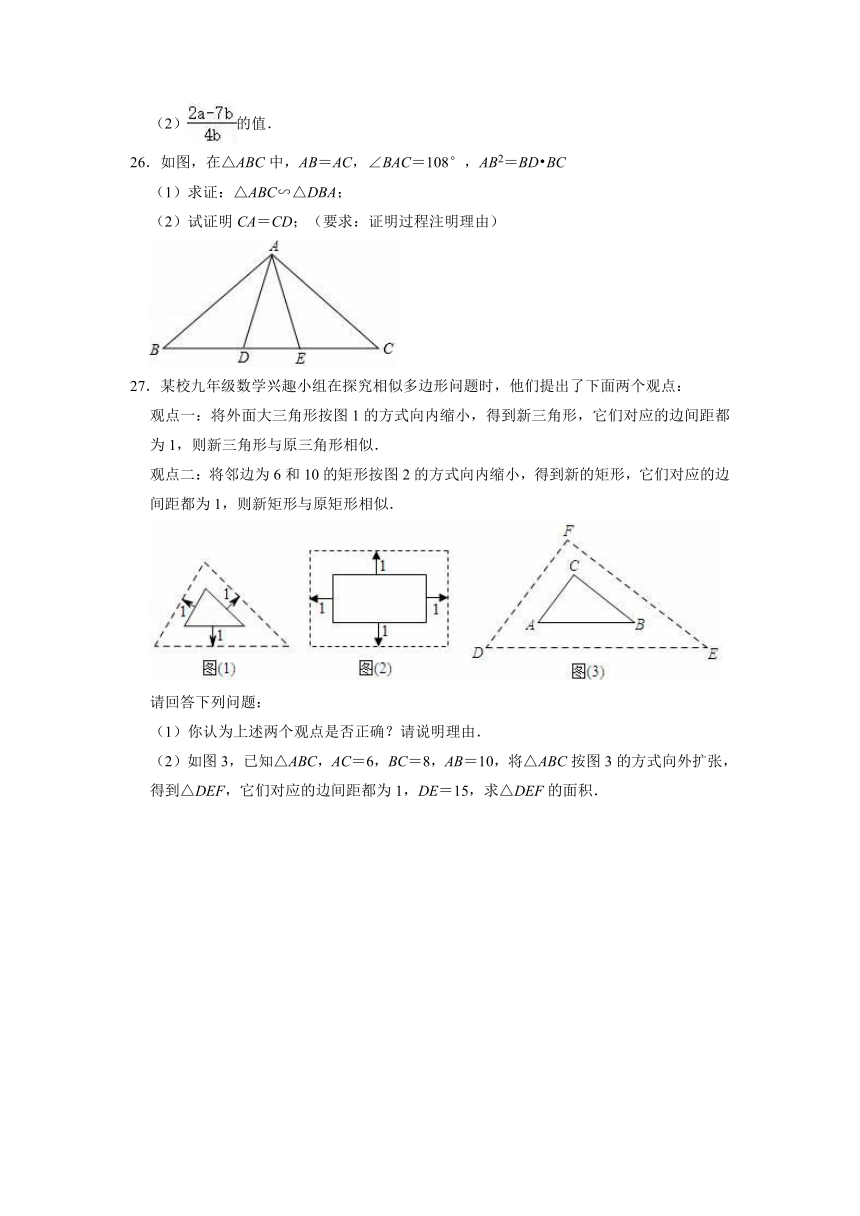
26.如图,在△ABC中,AB=AC,∠BAC=108°,AB2=BD BC
(1)求证:△ABC∽△DBA;
(2)试证明CA=CD;(要求:证明过程注明理由)
27.某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确?请说明理由.
(2)如图3,已知△ABC,AC=6,BC=8,AB=10,将△ABC按图3的方式向外扩张,得到△DEF,它们对应的边间距都为1,DE=15,求△DEF的面积.
参考答案与试题解析
一.选择题
1.解:∵,
∴设b=3k,a=2k,
∴==,
故选:B.
2.解:A、=,可以化成:xy=15,故此选项错误;
B、=,可以化成:3x=5y,故此选项正确;
C、=,可以化成:5x=3y,故此选项错误;
D、=,可以化成:5x=3y,故此选项错误.
故选:B.
3.解:A.4×10≠6×5,故不符合题意,
B.1×4≠2×3,故不符合题意,
C.≠2×3,故不符合题意,
D.,故符合题意,
故选:D.
4.解:A、所有等腰三角形都相似,错误,对应角不一定相等;
B、所有直角三角形都相似,错误,对应角不一定相等;
C、所有菱形都相似,错误,对应角不一定相等;
D、所有等边三角形都相似,正确.
故选:D.
5.解:∵=,
∴b=2a,
∴===,
故选:C.
6.解:∵四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,
∴∠E=∠A=80°,∠G=∠C=90°,
∴∠H=360°﹣∠E﹣∠F﹣∠G=360°﹣80°﹣70°﹣90°=120°,
故选:D.
7.解:∵相似多边形的面积比等于相似比的平方,面积比为25:36,
∴对应边的比为5:6,
故选:A.
8.解:∵,
∴AB2=2×(2﹣AB),
∴AB2+2AB﹣4=0,
解得,AB1=,AB2=﹣﹣1(舍去),
故选:C.
9.解:∵△ABC∽△DEF,
∴∠B=∠E=35°,∠C=∠F=80°,
∴∠D=180°﹣35°﹣80°=65°.
故选:C.
10.解:∵l1∥l2∥l3,
∴,
∵,
∴;
故选:A.
二.填空题
11.解:四边形ABCD∽四边形A′B′C′D′,
则∠B=∠B′=108°,∠C=∠C′=92′
四边形ABCD的内角和是360°,
因而∠D=360°﹣70°﹣108°﹣92°=90°.
12.解:①AD与AC是对应边时,
∵AB=24,AC=18,AD=12,
∴=,
即=,
解得AE=16;
②AD与AB是对应边时,
∵AB=24,AC=18,AD=12,
∴=,
即=,
解得AE=9,
∴AE=16或9.
故答案为:16或9.
13.解:过D作DM⊥BC于M,过B作BN⊥AD于N,如图:
∵AD∥BC,DM⊥BC,BN⊥AD,
∴四边形BMDN是矩形,DM=BN,
∵=,
∴=,
∴=,
∵AD∥BC,
∴==,
∴=,
∴=,
故答案为:.
14.解:∵,
∴2y=3(x﹣y),
整理,得3x=5y,
∴=.
故答案为.
15.解:由题意,设x=3k,y=5k,
∴==.
故答案为:
16.解:∵=,
∴==.
故答案为:.
17.解:设a、b的比例中项为λ,
∵a=4,b=8,
∴λ2=ab=32,
∴λ=±,
即a、b的比例中等于.
18.解:由于P为线段AB=2的黄金分割点,
且AP是较长线段;
则AP=AB=×2=﹣1.
故答案为﹣1.
19.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,
所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.
20.解:∵S四边形ABCD=2×4﹣×1×2﹣×1×2﹣1×1﹣×1×1=.
又∵四边形EFGH与四边形ABCD相似,
∴S四边形EFGH:S四边形ABCD=()2=()2=,
∴S四边形EFGH=×=.
故答案为:,.
三.解答题
21.解:∵b∥c,
∴,
∴OE=EF=,
∵a∥c,
∴,
∴DO=OF=×(+5)=,
∴DE=DO+OE=+=.
22.解:设===k(k≠0),
则a=5k,b=7k,c=8k,
代入3a﹣2b+c=9得,15k﹣14k+8k=9,
解得k=1,
所以,a=5,b=7,c=8,
所以,2a+4b﹣3c=2×5+4×7﹣3×8=10+28﹣24=14.
23.解:设===k,则a=9k,b=11k,c=14k,
∵a+b+c=68,
∴9k+11k+14k=68,
解得:k=2,
则a=18,b=22,c=28.
24.解:设AM=5x,则MB=11x,
∵AN:NB=5:7,
∴AN=AB=x,
∴x﹣5x=1.5,
解得x=0.9,
∴AB=16x=16×0.9=14.4.
∴AB长度为14.4.
25.解:∵a:b=3:2,
∴设a=3k,b=2k,
(1)==;
(2)==﹣1.
26.(1)证明:∵AB2=BD BC,
∴=,
∵∠B=∠B,
∴△ABC∽△DBA.
(2)证明:∵AB=AC,∠BAC=108°,
∴∠B=∠C=36°(等边对等角),
∵△ABC∽△DBA(已证)
∴∠BAD=∠C=36°(相似三角形的对应角相等)
∴∠CAD=72°(角的和差定义)
∴∠CDA=180°﹣∠C﹣∠CAD=72°(三角形内角和定理),
∴∠CAD=∠ADC(等量代换)
∴CA=CD(等角对等边).
27.解:(1)观点一正确;观点二不正确.
理由:①如图(1)连接并延长DA,交FC的延长线于点O,
∵△ABC和△DEF对应的边的距离都为1,
∴AB∥DE,AC∥DF,
∴∠FDO=∠CAO,∠ODE=∠OAB,
∴∠FDO+∠ODE=∠CAO+∠OAB,
即∠FDE=∠CAB,同理∠DEF=∠ABC,
∴△ABC∽△DEF,
∴观点一正确;
②如图(2)由题意可知,原矩形的邻边为6和10,
则新矩形邻边为4和8,
∵=,=,
∴,
∴新矩形于原矩形不相似,
∴观点二不正确;
(2)如图(3),延长DA、EB交于点O,
∵A到DE、DF的距离都为1,
∴DA是∠FDE的角平分线,
同理,EB是∠DEF的角平分线,
∴点O是△ABC的内心,
∵AC=6,BC=8,AB=10,
∴△ABC是直角三角形,
设△ABC的内切圆的半径为r,
则6﹣r+8﹣r=10,
解得r=2,
过点O作OH⊥DE于点H,交AB于G,
∵AB∥DE,
∴OG⊥AB,
∴OG=r=2,
∴==,
同理===,
∴DF=9,EF=12,
∴△DEF的面积为:×9×12=54.
一.选择题
1.若,则的值等于( )
A. B. C. D.
2.已知3x=5y(y≠0),则下列比例式成立的是( )
A.= B.= C.= D.=
3.下列各组的四条线段a,b,c,d是成比例线段的是( )
A.a=4,b=6,c=5,d=10 B.a=1,b=2,c=3,d=4
C.,b=3,c=2, D.a=2,,,
4.下列判断正确的是( )
A.所有等腰三角形都相似 B.所有直角三角形都相似
C.所有菱形都相似 D.所有等边三角形都相似
5.若=,则的值是( )
A.3 B. C. D.2
6.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠H等于( )
A.70° B.80° C.110° D.120°
7.若两个相似多边形的面积比为25:36,则它们的对应边的比是( )
A.5:6 B.6:5 C.25:36 D.36:25
8.如图,点B在线段AC上,且,设AC=2,则AB的长为( )
A. B. C. D.
9.如图所示,△ABC∽△DEF,则∠D的度数为( )
A.35° B.45° C.65° D.80°
10.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,若,则的值为( )
A. B. C. D.
二.填空题
11.四边形ABCD∽四边形A′B′C′D′,∠A=70°,∠B′=108°,∠C′=92°,则∠D= 度.
12.如图,在三角形ABC中,AB=24,AC=18,D是AC上一点AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE= .
13.如图所示,已知在梯形ABCD中,AD∥BC,=,则= .
14.如果,那么= .
15.已知,则= .
16.若=,则的值等于 .
17.已知线段a=4,b=8,则a、b的比例中项线段等于 .
18.若点P是线段AB的黄金分割点,且AP>BP,AB=2,则AP= .(保留根号)
19.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
20.如图所示的正方形网格中,每个小正方形的边长均为1,四边形ABCD的面积是 .若四边形EFGH与四边形ABCD相似,则四边形EFGH的面积是 .
三.解答题
21.如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度.
22.已知==,且3a﹣2b+c=9,求2a+4b﹣3c的值.
23.已知==,且a+b+c=68.求a、b、c的值.
24.如图,已知线段AB上有两点M,N,满足AM:MB=5:11,AN:NB=5:7,NM=1.5,求AB的长.
25.已知a:b=3:2,求:
(1);
(2)的值.
26.如图,在△ABC中,AB=AC,∠BAC=108°,AB2=BD BC
(1)求证:△ABC∽△DBA;
(2)试证明CA=CD;(要求:证明过程注明理由)
27.某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确?请说明理由.
(2)如图3,已知△ABC,AC=6,BC=8,AB=10,将△ABC按图3的方式向外扩张,得到△DEF,它们对应的边间距都为1,DE=15,求△DEF的面积.
参考答案与试题解析
一.选择题
1.解:∵,
∴设b=3k,a=2k,
∴==,
故选:B.
2.解:A、=,可以化成:xy=15,故此选项错误;
B、=,可以化成:3x=5y,故此选项正确;
C、=,可以化成:5x=3y,故此选项错误;
D、=,可以化成:5x=3y,故此选项错误.
故选:B.
3.解:A.4×10≠6×5,故不符合题意,
B.1×4≠2×3,故不符合题意,
C.≠2×3,故不符合题意,
D.,故符合题意,
故选:D.
4.解:A、所有等腰三角形都相似,错误,对应角不一定相等;
B、所有直角三角形都相似,错误,对应角不一定相等;
C、所有菱形都相似,错误,对应角不一定相等;
D、所有等边三角形都相似,正确.
故选:D.
5.解:∵=,
∴b=2a,
∴===,
故选:C.
6.解:∵四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,
∴∠E=∠A=80°,∠G=∠C=90°,
∴∠H=360°﹣∠E﹣∠F﹣∠G=360°﹣80°﹣70°﹣90°=120°,
故选:D.
7.解:∵相似多边形的面积比等于相似比的平方,面积比为25:36,
∴对应边的比为5:6,
故选:A.
8.解:∵,
∴AB2=2×(2﹣AB),
∴AB2+2AB﹣4=0,
解得,AB1=,AB2=﹣﹣1(舍去),
故选:C.
9.解:∵△ABC∽△DEF,
∴∠B=∠E=35°,∠C=∠F=80°,
∴∠D=180°﹣35°﹣80°=65°.
故选:C.
10.解:∵l1∥l2∥l3,
∴,
∵,
∴;
故选:A.
二.填空题
11.解:四边形ABCD∽四边形A′B′C′D′,
则∠B=∠B′=108°,∠C=∠C′=92′
四边形ABCD的内角和是360°,
因而∠D=360°﹣70°﹣108°﹣92°=90°.
12.解:①AD与AC是对应边时,
∵AB=24,AC=18,AD=12,
∴=,
即=,
解得AE=16;
②AD与AB是对应边时,
∵AB=24,AC=18,AD=12,
∴=,
即=,
解得AE=9,
∴AE=16或9.
故答案为:16或9.
13.解:过D作DM⊥BC于M,过B作BN⊥AD于N,如图:
∵AD∥BC,DM⊥BC,BN⊥AD,
∴四边形BMDN是矩形,DM=BN,
∵=,
∴=,
∴=,
∵AD∥BC,
∴==,
∴=,
∴=,
故答案为:.
14.解:∵,
∴2y=3(x﹣y),
整理,得3x=5y,
∴=.
故答案为.
15.解:由题意,设x=3k,y=5k,
∴==.
故答案为:
16.解:∵=,
∴==.
故答案为:.
17.解:设a、b的比例中项为λ,
∵a=4,b=8,
∴λ2=ab=32,
∴λ=±,
即a、b的比例中等于.
18.解:由于P为线段AB=2的黄金分割点,
且AP是较长线段;
则AP=AB=×2=﹣1.
故答案为﹣1.
19.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,
所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.
20.解:∵S四边形ABCD=2×4﹣×1×2﹣×1×2﹣1×1﹣×1×1=.
又∵四边形EFGH与四边形ABCD相似,
∴S四边形EFGH:S四边形ABCD=()2=()2=,
∴S四边形EFGH=×=.
故答案为:,.
三.解答题
21.解:∵b∥c,
∴,
∴OE=EF=,
∵a∥c,
∴,
∴DO=OF=×(+5)=,
∴DE=DO+OE=+=.
22.解:设===k(k≠0),
则a=5k,b=7k,c=8k,
代入3a﹣2b+c=9得,15k﹣14k+8k=9,
解得k=1,
所以,a=5,b=7,c=8,
所以,2a+4b﹣3c=2×5+4×7﹣3×8=10+28﹣24=14.
23.解:设===k,则a=9k,b=11k,c=14k,
∵a+b+c=68,
∴9k+11k+14k=68,
解得:k=2,
则a=18,b=22,c=28.
24.解:设AM=5x,则MB=11x,
∵AN:NB=5:7,
∴AN=AB=x,
∴x﹣5x=1.5,
解得x=0.9,
∴AB=16x=16×0.9=14.4.
∴AB长度为14.4.
25.解:∵a:b=3:2,
∴设a=3k,b=2k,
(1)==;
(2)==﹣1.
26.(1)证明:∵AB2=BD BC,
∴=,
∵∠B=∠B,
∴△ABC∽△DBA.
(2)证明:∵AB=AC,∠BAC=108°,
∴∠B=∠C=36°(等边对等角),
∵△ABC∽△DBA(已证)
∴∠BAD=∠C=36°(相似三角形的对应角相等)
∴∠CAD=72°(角的和差定义)
∴∠CDA=180°﹣∠C﹣∠CAD=72°(三角形内角和定理),
∴∠CAD=∠ADC(等量代换)
∴CA=CD(等角对等边).
27.解:(1)观点一正确;观点二不正确.
理由:①如图(1)连接并延长DA,交FC的延长线于点O,
∵△ABC和△DEF对应的边的距离都为1,
∴AB∥DE,AC∥DF,
∴∠FDO=∠CAO,∠ODE=∠OAB,
∴∠FDO+∠ODE=∠CAO+∠OAB,
即∠FDE=∠CAB,同理∠DEF=∠ABC,
∴△ABC∽△DEF,
∴观点一正确;
②如图(2)由题意可知,原矩形的邻边为6和10,
则新矩形邻边为4和8,
∵=,=,
∴,
∴新矩形于原矩形不相似,
∴观点二不正确;
(2)如图(3),延长DA、EB交于点O,
∵A到DE、DF的距离都为1,
∴DA是∠FDE的角平分线,
同理,EB是∠DEF的角平分线,
∴点O是△ABC的内心,
∵AC=6,BC=8,AB=10,
∴△ABC是直角三角形,
设△ABC的内切圆的半径为r,
则6﹣r+8﹣r=10,
解得r=2,
过点O作OH⊥DE于点H,交AB于G,
∵AB∥DE,
∴OG⊥AB,
∴OG=r=2,
∴==,
同理===,
∴DF=9,EF=12,
∴△DEF的面积为:×9×12=54.
