2.4用单摆测量重力加速度 自主提升过关练(word版含答案)
文档属性
| 名称 | 2.4用单摆测量重力加速度 自主提升过关练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 462.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-15 07:28:12 | ||
图片预览



文档简介
2.4用单摆测量重力加速度 自主提升过关练(含解析)
一、选择题
1.在利用单摆测定重力加速度的实验中,下列说法正确的是
A.把单摆从平衡位置拉开的摆角,并在释放摆球的同时开始计时
B.测量摆球通过最低点100次的时间t,则单摆周期为
C.用悬线的长度加摆球的直径作为摆长,代入单摆周期公式计算得到的重力加速度值偏大
D.选择密度较小的摆球,测得的重力加速度值误差较小
2.用单摆测重力加速度的实验中,测出的重力加速度的值大于当地的重力加速度,下列原因中可能的是( )
A.振幅太小导致测得的周期偏小
B.计算摆长时,只考虑线长,没有加上摆球半径
C.将n次全振动误记为(n-1)次全振动
D.将n次全振动误记为(n+1)次全振动
3.在利用单摆测重力加速度的实验中,下列哪些操作会使得测得的重力加速度 g 的值偏大( )
A.摆线过长,摆角过小
B.在测量摆长时,将线长和小球直径之和作为了摆长
C.摆球的质量过大
D.测量周期时,时间t内全振动次数少数了一次
4.以下实验不需要打点计时器的是( )
A.研究匀变速直线运动 B.验证牛顿运动定律
C.探究动能定理 D.用单摆测定重力加速度
5.某同学利用如图甲所示的单摆测量当地重力加速度,他通过多次改变摆长,并测出不同摆长对应的周期,作出的图像如图乙所示。下列选项正确的是( )
A.为减小误差,应尽量增大摆角
B.为减小误差,应尽量选择质量较大、体积较小的摆球
C.为减小误差,测周期时应从摆球经过最低点时开始计时
D.图乙中图线延长线不过坐标原点的原因可能是将摆球的直径计入了摆长
E.由图乙可得,当地重力加速度
6.在“利用单摆测重力加速度”的实验中,如果得出的重力加速度的测量值偏大,其可能的原因是( )
A.测量周期时,时间内全振动的次数少数了一次
B.测量周期时,时间内全振动的次数多数了一次
C.摆线上端固定不牢固,振动中出现松动,使摆线变长
D.在测量摆长时,将细线的长度加上小球的直径作为摆长.
E.小球没有在同一竖直面内运动,形成了圆锥摆
7.在“探究单摆周期与摆长的关系”的实验中,下列说法正确的是( )
A.制作单摆时,应选用密度较大的实心金属小球
B.记录摆长时,将摆线长与小球直径相加
C.小球摆角应较小,近似满足简谐运动条件
D.测出一次摆长和对应的周期,可以得出周期与摆长的关系
二、实验题
8.某同学利用单摆测定当地的重力加速度。
(1)实验室已经提供的器材有:铁架台、夹子、秒表、游标卡尺。除此之外,还需要的器材有____。
A.长度约为1m的细线 B.长度约为30cm的细线
C.直径约为2cm的钢球 D.直径约为2cm的木球
E.最小刻度为1cm的直尺 F.最小刻度为1mm的直尺
(2)为了减小测量周期的误差,实验时需要在适当的位置做一标记,当摆球通过该标记时开始计时,该标记应该放置在摆球摆动的______。
A.最高点 B.最低点 C.任意位置
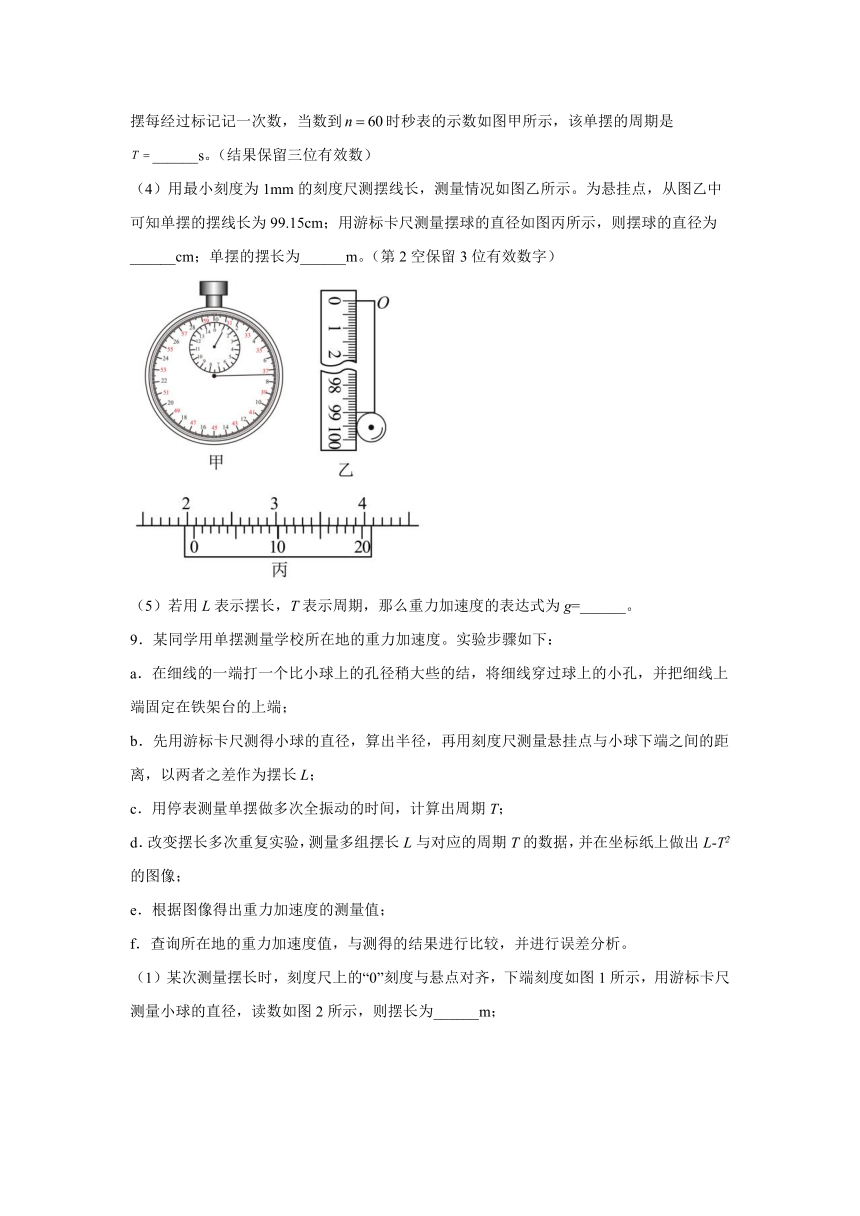
(3)用秒表测量单摆的周期。当单摆摆动稳定且到达计时标记时开始计时并记为,单摆每经过标记记一次数,当数到时秒表的示数如图甲所示,该单摆的周期是______s。(结果保留三位有效数)
(4)用最小刻度为1mm的刻度尺测摆线长,测量情况如图乙所示。为悬挂点,从图乙中可知单摆的摆线长为99.15cm;用游标卡尺测量摆球的直径如图丙所示,则摆球的直径为______cm;单摆的摆长为______m。(第2空保留3位有效数字)
(5)若用L表示摆长,T表示周期,那么重力加速度的表达式为g=______。
9.某同学用单摆测量学校所在地的重力加速度。实验步骤如下:
a.在细线的一端打一个比小球上的孔径稍大些的结,将细线穿过球上的小孔,并把细线上端固定在铁架台的上端;
b.先用游标卡尺测得小球的直径,算出半径,再用刻度尺测量悬挂点与小球下端之间的距离,以两者之差作为摆长L;
c.用停表测量单摆做多次全振动的时间,计算出周期T;
d.改变摆长多次重复实验,测量多组摆长L与对应的周期T的数据,并在坐标纸上做出L-T2的图像;
e.根据图像得出重力加速度的测量值;
f.查询所在地的重力加速度值,与测得的结果进行比较,并进行误差分析。
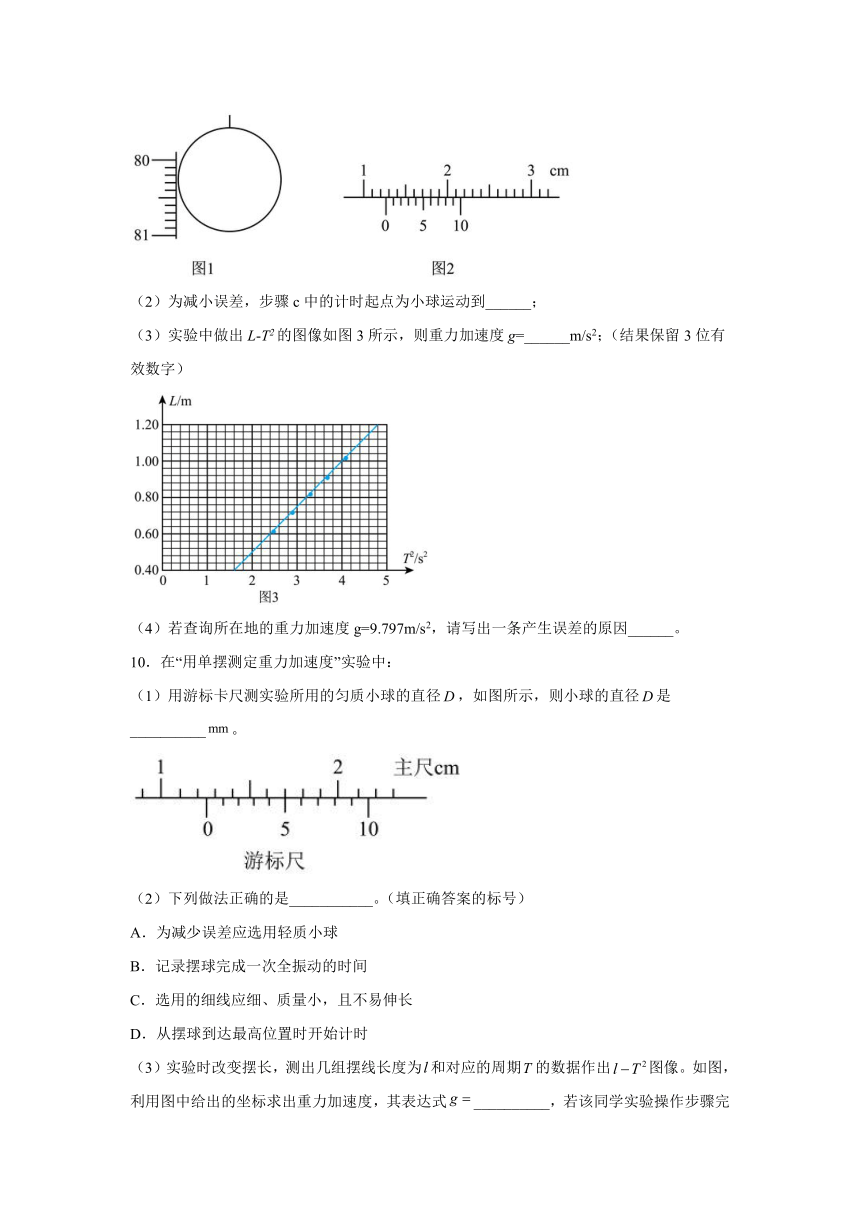
(1)某次测量摆长时,刻度尺上的“0”刻度与悬点对齐,下端刻度如图1所示,用游标卡尺测量小球的直径,读数如图2所示,则摆长为______m;
(2)为减小误差,步骤c中的计时起点为小球运动到______;
(3)实验中做出L-T2的图像如图3所示,则重力加速度g=______m/s2;(结果保留3位有效数字)
(4)若查询所在地的重力加速度g=9.797m/s2,请写出一条产生误差的原因______。
10.在“用单摆测定重力加速度”实验中:
(1)用游标卡尺测实验所用的匀质小球的直径,如图所示,则小球的直径是__________。
(2)下列做法正确的是___________。(填正确答案的标号)
A.为减少误差应选用轻质小球
B.记录摆球完成一次全振动的时间
C.选用的细线应细、质量小,且不易伸长
D.从摆球到达最高位置时开始计时
(3)实验时改变摆长,测出几组摆线长度为和对应的周期的数据作出图像。如图,利用图中给出的坐标求出重力加速度,其表达式__________,若该同学实验操作步骤完全正确,那么纵轴截距的绝对值是____________。(用表示)
11.小福同学做“用单摆测量重力加速度的大小”实验。
(1)下列最合理的装置是_____;
A. B. C. D.
(2)该同学根据实验数据,利用计算机拟合得到的方程为:T2=4.04l+0.05。由此可以得出当地重力加速度g=__________m/s2(π取3.14,结果保留3位有效数字),从方程中可知T2与l没有成正比关系,其原因可能是_______。
A.开始计时时,小球可能在最高点 B.小球摆动过程中,可能摆角太大
C.计算摆长时,可能加了小球的直径 D.计算摆长时,可能忘了加小球半径
12.某同学在做“利用单摆测重力加速度”的实验中,先测得摆线长为101.00cm,摆球直径为2.00cm,然后用秒表记录了单摆振动50次所用的时间为101.5s。
(1)他测得的重力加速度___________。(计算结果取三位有效数字)
(2)他测得的g值偏小,可能原因是___________。(填正确选项前字母)
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时,秒表未及时按下
D.实验中误将49次全振动计为50次
(3)为了提高实验精确度,在实验中可改变几次摆长L并测出相应的周期T,从而得出一组对应的L和T的数值,再以L为横坐标,为纵坐标将所得数据描点后连成直线,并求得该直线的斜率为k。则重力加速度___________。(用k表示)
13.小华同学在做“用单摆测定重力加速度”的实验。
(1)用游标卡尺测小球的直径时示数如图甲所示,则小球的直径________。
(2)在实验中,若测得的重力加速度值偏大,其原因可能是_______。
A.所用摆球质量偏大
B.振幅太小导致测得的周期偏小
C.将n次摆动的时间误记为次摆动的时间
D.单摆的悬点未固定紧,振动中出现松动,摆长变大
(3)小华同学用标准的实验器材和正确的实验方法测量出几组不同摆长和对应的周期,然后根据数据描绘图像,进一步计算得到图像的斜率为,可知当地的重力加速度大小________(用含k的表达式表示)。
14.利用单摆可以测量地球的重力加速度g,若摆线长为L,摆球直径为D,周期为T,则当地的重力加速度_____利用单摆的等时性,人们制成了摆钟。若地球上标准钟秒针转一周用时,已知,那么将该钟拿到月球上时,秒针转一周所用的时间为_____s(保留到整数位)。
15.某同学做“利用单摆测重力加速度”实验,先用一个游标卡尺测量小球的直径,示数如图甲所示,则该小球的直径为________mm。用秒表测得50个全振动的时间如图乙所示,秒表示数为__________s 。
16.某同学在家里测重力加速度。他找到细线和铁锁,制成一个单摆,如图所示。由于家里只有一根量程为30cm的刻度尺。于是他在细线上的A点做了一个标记,使得悬点O到A点间的细线长度小于刻度尺量程。保持该标记以下的细线长度不变,通过改变O、A间细线长度以改变摆长。实验中,当O、A间细线的长度分别为l1、l2时,测得相应单摆的周期为T1、T2。由此可得重力加速度g=________(用l1、l2、T1、T2表示)。
17.有两个同学利用假期分别去参观北大和南大的物理实验室,各自在那里利用先进的系统较准确地探究了“单摆的周期与摆长的关系”,他们通过校园网交换实验数据,并由计算机绘制了图象,如图甲所示。去北大的同学所测实验结果对应的图线是_______选填“A”或“B”。另外,在南大做探究的同学还利用计算机绘制了在南大实验室摆动的两种摆长的振动图象如图乙,由图可知,两单摆摆长之比________。
试卷第页,共页
参考答案:
1.C
【解析】
A.单摆在摆角很小的情况下才做简谐运动,则单摆偏离平衡位置的角度不能太大,一般不超过,把单摆从平衡位置拉开的摆角,单摆的运动不是简谐运动,故A错误;
B.测量摆球通过最低点100次的时间t,则单摆周期为
故B错误;
C.由单摆周期公式
可知,用悬线的长度加摆球的直径作为摆长,单摆摆长L偏大,由可知,所测重力加速度偏大,故C正确;
D.单摆在运动过程中要受到空气阻力作用,为减小实验误差应选择质量大而体积小,即密度大的球作为摆球,故D错误。
故选C。
2.D
【解析】
A.单摆周期与振幅无关,振幅的大小不会影响周期的测量,A错误;
B.由
得,重力加速度
测得的g偏大,可能是L的测量值偏大,也可能是T的测量值偏小,所以不加摆球半径,是使L偏小,使g偏小,B错误;
C.将n次全振动记为(n-1)次全振动,则T的测量值偏大,使g偏小,C错误;
D.将n次全振动记为(n+1)次全振动,T的测量值偏小,使g偏大,D正确。
故选D。
3.B
【解析】
AC.摆线过长、摆角过小、质量过大对测量结果都没有影响,故AC错误;
BD.根据
得
可知在测量摆长时,将线长和小球直径之和作为了摆长,偏大,偏大;测量周期时,时间t内全振动次数少数了一次,则周期偏大,偏小。故B正确,D错误。
故选B。
4.D
【解析】
A.研究匀变速直线运动,需要打点计时器和纸带来测物体运动的速度和加速度,所以A错误;
B.验证牛顿运动定律,需要打点计时器和纸带来测物体运动的加速度,所以B错误;
C.探究动能定理,需要打点计时器和纸带来测物体运动的速度,所以C错误;
D.用单摆测定重力加速度,不需要打点计时器,使用秒表计时,所以D正确。
故选D。
5.BCE
【解析】
A.单摆在摆角小于5°时的运动是简谐运动,单摆的摆角不能太大,A错误;
B.为减小空气阻力对实验的影响,应选体积较小、质量较大的摆球,B正确;
C.为减小周期测量误差,测量周期时,应取摆球通过最低点做为计时的起、终点位置,C正确;
D.图像不通过坐标原点,从图像可以得到相同的周期下,摆长偏小,故可能是漏加小球半径,D错误;
E.根据
则
解得
E正确。
故选BCE。
6.BDE
【解析】
由单摆的周期公式得
A.数振动次数时,少计了一次,则求出的周期T偏大,由知测量值偏小,则A错误;
B.数振动次数时,多计了一次,则求出的周期T偏小,由知测量值偏大,则B正确;
C.振动中出现松动,使摆线变长,测得的周期变大,则由可知测量值偏小,C错误;
D.测量摆长时,将细线的长度加上小球的直径作为摆长,则由可知测量值偏大,则D正确;
E.形成圆锥摆,如图所示:
根据向心力计算公式可得
解得
则周期偏小,g测量值偏大,则E正确;
故选BDE。
7.AC
【解析】
A.在制作单摆时,摆球直径要尽量远远小于摆线长,摆球质量的选择应远远大于摆线质量,这样才能接近单摆的理想条件,A正确;
B.摆长为悬点到球心的距离,即摆长等于摆线长加小球半径,B错误;
C.要保证单摆做简谐运动,摆角要小于5 ,C正确;
D.实验中为减小误差,测周期时一般需要测出单摆完成n次全振动需要的时间t,然后求出周期,故D错误.
故选AC.
8. ACF B 2.29 2.075 1.00
【解析】
【详解】
(1)AB.为了减小误差,摆线应选择尽量长些的,故A符合题意,B不符合题意;
CD.为了减小空气阻力对实验的影响,摆球应选择密度较大的钢球,故C符合题意,D不符合题意;
EF.实验中需要测量细线的长度,为了能够更加精确,应选择最小刻度为1mm的直尺,故E不符合题意,F符合题意。
故选ACF.
(2)当摆球运动至最低点时速度最大,以此作为计时标记位置对时间的测量相对误差最小,故选B。
(3)秒表读数为
该单摆的周期为
(4)摆球的直径为
摆线长为
所以单摆的摆长为
(5)根据单摆周期公式
可得
9. 0.8034 平衡位置 摆长的测量值偏小或周期的测量值偏大
【解析】
【详解】
(1)如图所示
可知刻度尺的读数为80.97cm,游标卡尺的读数为12.6mm,故小球的半径为6.3mm,故摆长为
(2)由于实际摆动过程最高点的位置会发生变化,且在最高点附近速度较小,为减小误差,步骤c中的计时起点为小球运动到平衡位置。
(3)单摆的周期公式为
整理得
由图线的斜率可得
解得
(4)若查询所在地的重力加速度g=9.797m/s2,可知测量值偏小,由周期公式可得
故可能的原因是:摆长的测量值偏小或周期的测量值偏大。
10. 12.5 C
【解析】
【详解】
(1)小球的直径为
(2) A.为减少误差应选用密度较大、体积较小的小球,A错误;
B.应记录摆球完成次全振动的时间,再计算周期,B错误;
C.选用的细线应细、质量小,且不易伸长,C正确;
D.计时起点应从摆球经过最低点时开始计时,D错误。
故选C。
(3)据单摆周期公式可得
整理得
可知,图线的斜率为
故重力加速度的表达式为
当时,,可知纵轴截距的绝对值是小球的半径。
11. D 9.76 D
【解析】
(1)单摆摆动过程中,摆线要求长度不变,摆线应该选择弹性小的细线,且摆球应选择密度大的铁球,以减小阻力的影响,故选D;
(2)根据单摆周期公式
有
而T2=4.04l+0.05,从方程中可知
解得
从方程中可知T2与l没有成正比,说明l等于0,周期不为0,即可能忘了加小球半径,与小球的计时位置,及小球摆角均无关;故选D。
12. 9.76 B
【解析】
【详解】
(1)摆长
周期
则由公式
可得
(2)A.测摆线长时摆线拉得过紧,会使摆长的测量值偏大,则g测量值偏大,A错误;
B.由公式
知当实际摆长变长时,实际的周期就变大,那么测量的加速度就变小,B正确;
C.开始计时时,秒表过迟按下,会使周期T的测量值偏小,则g测量值偏大,C错误;
D.实验中误将49次全振动计为50次,会使周期T的测量值偏小,则g测量值偏大,D错误。
故选B。
(3)把公式
变为
易知斜率
则
13. 2.18 C
【解析】
【详解】
(1)游标卡尺读数是主尺读数(mm的整数位)加上游标尺读数(mm的小数位),由甲图可读出游标卡尺读数为。
(2)AB.由单摆周期公式得
周期测量值
可知重力加速度测量值偏大与摆球质量、振幅(不能太大)无关;AB错误;
D.单摆的悬点为固定,导致摆长变大,但是数据处理仍旧按照原来的摆长来计算加速度则测量值偏小,D错误;
C.将n次摆动当成(n+1)次则周期变小,因此测量值偏大,C正确;
故选C。
(3)由可得
则图像的斜率
得
14. 147
【解析】
单摆的摆长
由单摆的周期公式
可得
地球上标准钟秒针转一周用时,则在月球上
15. 29.8mm 99.8s
【解析】
【详解】
图甲所示游标卡尺主尺的示数是29mm,游标尺的示数是8×0.1mm=0.8mm,
小球的直径d=29mm+0.8mm=29.8mm;
图乙所示秒表分针示数是1.5min,秒针示数是9.8s,秒表所示是90s+9.8s=99.8s
16.
【解析】
设A到铁锁重心的距离为l,则第1、2次的摆长分别为l+l1、l+l2,由
T1=2π
T2=2π
联立解得
g=
17. B
【解析】
根据单摆的周期公式可得
根据图甲可知
即
因为从赤道到两级重力加速度变大,故在北大的斜率小,因此是B;
由图乙可知
两摆的摆长之比等于周期的平方比,由
,
可得摆长比为。
试卷第页,共页
一、选择题
1.在利用单摆测定重力加速度的实验中,下列说法正确的是
A.把单摆从平衡位置拉开的摆角,并在释放摆球的同时开始计时
B.测量摆球通过最低点100次的时间t,则单摆周期为
C.用悬线的长度加摆球的直径作为摆长,代入单摆周期公式计算得到的重力加速度值偏大
D.选择密度较小的摆球,测得的重力加速度值误差较小
2.用单摆测重力加速度的实验中,测出的重力加速度的值大于当地的重力加速度,下列原因中可能的是( )
A.振幅太小导致测得的周期偏小
B.计算摆长时,只考虑线长,没有加上摆球半径
C.将n次全振动误记为(n-1)次全振动
D.将n次全振动误记为(n+1)次全振动
3.在利用单摆测重力加速度的实验中,下列哪些操作会使得测得的重力加速度 g 的值偏大( )
A.摆线过长,摆角过小
B.在测量摆长时,将线长和小球直径之和作为了摆长
C.摆球的质量过大
D.测量周期时,时间t内全振动次数少数了一次
4.以下实验不需要打点计时器的是( )
A.研究匀变速直线运动 B.验证牛顿运动定律
C.探究动能定理 D.用单摆测定重力加速度
5.某同学利用如图甲所示的单摆测量当地重力加速度,他通过多次改变摆长,并测出不同摆长对应的周期,作出的图像如图乙所示。下列选项正确的是( )
A.为减小误差,应尽量增大摆角
B.为减小误差,应尽量选择质量较大、体积较小的摆球
C.为减小误差,测周期时应从摆球经过最低点时开始计时
D.图乙中图线延长线不过坐标原点的原因可能是将摆球的直径计入了摆长
E.由图乙可得,当地重力加速度
6.在“利用单摆测重力加速度”的实验中,如果得出的重力加速度的测量值偏大,其可能的原因是( )
A.测量周期时,时间内全振动的次数少数了一次
B.测量周期时,时间内全振动的次数多数了一次
C.摆线上端固定不牢固,振动中出现松动,使摆线变长
D.在测量摆长时,将细线的长度加上小球的直径作为摆长.
E.小球没有在同一竖直面内运动,形成了圆锥摆
7.在“探究单摆周期与摆长的关系”的实验中,下列说法正确的是( )
A.制作单摆时,应选用密度较大的实心金属小球
B.记录摆长时,将摆线长与小球直径相加
C.小球摆角应较小,近似满足简谐运动条件
D.测出一次摆长和对应的周期,可以得出周期与摆长的关系
二、实验题
8.某同学利用单摆测定当地的重力加速度。
(1)实验室已经提供的器材有:铁架台、夹子、秒表、游标卡尺。除此之外,还需要的器材有____。
A.长度约为1m的细线 B.长度约为30cm的细线
C.直径约为2cm的钢球 D.直径约为2cm的木球
E.最小刻度为1cm的直尺 F.最小刻度为1mm的直尺
(2)为了减小测量周期的误差,实验时需要在适当的位置做一标记,当摆球通过该标记时开始计时,该标记应该放置在摆球摆动的______。
A.最高点 B.最低点 C.任意位置
(3)用秒表测量单摆的周期。当单摆摆动稳定且到达计时标记时开始计时并记为,单摆每经过标记记一次数,当数到时秒表的示数如图甲所示,该单摆的周期是______s。(结果保留三位有效数)
(4)用最小刻度为1mm的刻度尺测摆线长,测量情况如图乙所示。为悬挂点,从图乙中可知单摆的摆线长为99.15cm;用游标卡尺测量摆球的直径如图丙所示,则摆球的直径为______cm;单摆的摆长为______m。(第2空保留3位有效数字)
(5)若用L表示摆长,T表示周期,那么重力加速度的表达式为g=______。
9.某同学用单摆测量学校所在地的重力加速度。实验步骤如下:
a.在细线的一端打一个比小球上的孔径稍大些的结,将细线穿过球上的小孔,并把细线上端固定在铁架台的上端;
b.先用游标卡尺测得小球的直径,算出半径,再用刻度尺测量悬挂点与小球下端之间的距离,以两者之差作为摆长L;
c.用停表测量单摆做多次全振动的时间,计算出周期T;
d.改变摆长多次重复实验,测量多组摆长L与对应的周期T的数据,并在坐标纸上做出L-T2的图像;
e.根据图像得出重力加速度的测量值;
f.查询所在地的重力加速度值,与测得的结果进行比较,并进行误差分析。
(1)某次测量摆长时,刻度尺上的“0”刻度与悬点对齐,下端刻度如图1所示,用游标卡尺测量小球的直径,读数如图2所示,则摆长为______m;
(2)为减小误差,步骤c中的计时起点为小球运动到______;
(3)实验中做出L-T2的图像如图3所示,则重力加速度g=______m/s2;(结果保留3位有效数字)
(4)若查询所在地的重力加速度g=9.797m/s2,请写出一条产生误差的原因______。
10.在“用单摆测定重力加速度”实验中:
(1)用游标卡尺测实验所用的匀质小球的直径,如图所示,则小球的直径是__________。
(2)下列做法正确的是___________。(填正确答案的标号)
A.为减少误差应选用轻质小球
B.记录摆球完成一次全振动的时间
C.选用的细线应细、质量小,且不易伸长
D.从摆球到达最高位置时开始计时
(3)实验时改变摆长,测出几组摆线长度为和对应的周期的数据作出图像。如图,利用图中给出的坐标求出重力加速度,其表达式__________,若该同学实验操作步骤完全正确,那么纵轴截距的绝对值是____________。(用表示)
11.小福同学做“用单摆测量重力加速度的大小”实验。
(1)下列最合理的装置是_____;
A. B. C. D.
(2)该同学根据实验数据,利用计算机拟合得到的方程为:T2=4.04l+0.05。由此可以得出当地重力加速度g=__________m/s2(π取3.14,结果保留3位有效数字),从方程中可知T2与l没有成正比关系,其原因可能是_______。
A.开始计时时,小球可能在最高点 B.小球摆动过程中,可能摆角太大
C.计算摆长时,可能加了小球的直径 D.计算摆长时,可能忘了加小球半径
12.某同学在做“利用单摆测重力加速度”的实验中,先测得摆线长为101.00cm,摆球直径为2.00cm,然后用秒表记录了单摆振动50次所用的时间为101.5s。
(1)他测得的重力加速度___________。(计算结果取三位有效数字)
(2)他测得的g值偏小,可能原因是___________。(填正确选项前字母)
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时,秒表未及时按下
D.实验中误将49次全振动计为50次
(3)为了提高实验精确度,在实验中可改变几次摆长L并测出相应的周期T,从而得出一组对应的L和T的数值,再以L为横坐标,为纵坐标将所得数据描点后连成直线,并求得该直线的斜率为k。则重力加速度___________。(用k表示)
13.小华同学在做“用单摆测定重力加速度”的实验。
(1)用游标卡尺测小球的直径时示数如图甲所示,则小球的直径________。
(2)在实验中,若测得的重力加速度值偏大,其原因可能是_______。
A.所用摆球质量偏大
B.振幅太小导致测得的周期偏小
C.将n次摆动的时间误记为次摆动的时间
D.单摆的悬点未固定紧,振动中出现松动,摆长变大
(3)小华同学用标准的实验器材和正确的实验方法测量出几组不同摆长和对应的周期,然后根据数据描绘图像,进一步计算得到图像的斜率为,可知当地的重力加速度大小________(用含k的表达式表示)。
14.利用单摆可以测量地球的重力加速度g,若摆线长为L,摆球直径为D,周期为T,则当地的重力加速度_____利用单摆的等时性,人们制成了摆钟。若地球上标准钟秒针转一周用时,已知,那么将该钟拿到月球上时,秒针转一周所用的时间为_____s(保留到整数位)。
15.某同学做“利用单摆测重力加速度”实验,先用一个游标卡尺测量小球的直径,示数如图甲所示,则该小球的直径为________mm。用秒表测得50个全振动的时间如图乙所示,秒表示数为__________s 。
16.某同学在家里测重力加速度。他找到细线和铁锁,制成一个单摆,如图所示。由于家里只有一根量程为30cm的刻度尺。于是他在细线上的A点做了一个标记,使得悬点O到A点间的细线长度小于刻度尺量程。保持该标记以下的细线长度不变,通过改变O、A间细线长度以改变摆长。实验中,当O、A间细线的长度分别为l1、l2时,测得相应单摆的周期为T1、T2。由此可得重力加速度g=________(用l1、l2、T1、T2表示)。
17.有两个同学利用假期分别去参观北大和南大的物理实验室,各自在那里利用先进的系统较准确地探究了“单摆的周期与摆长的关系”,他们通过校园网交换实验数据,并由计算机绘制了图象,如图甲所示。去北大的同学所测实验结果对应的图线是_______选填“A”或“B”。另外,在南大做探究的同学还利用计算机绘制了在南大实验室摆动的两种摆长的振动图象如图乙,由图可知,两单摆摆长之比________。
试卷第页,共页
参考答案:
1.C
【解析】
A.单摆在摆角很小的情况下才做简谐运动,则单摆偏离平衡位置的角度不能太大,一般不超过,把单摆从平衡位置拉开的摆角,单摆的运动不是简谐运动,故A错误;
B.测量摆球通过最低点100次的时间t,则单摆周期为
故B错误;
C.由单摆周期公式
可知,用悬线的长度加摆球的直径作为摆长,单摆摆长L偏大,由可知,所测重力加速度偏大,故C正确;
D.单摆在运动过程中要受到空气阻力作用,为减小实验误差应选择质量大而体积小,即密度大的球作为摆球,故D错误。
故选C。
2.D
【解析】
A.单摆周期与振幅无关,振幅的大小不会影响周期的测量,A错误;
B.由
得,重力加速度
测得的g偏大,可能是L的测量值偏大,也可能是T的测量值偏小,所以不加摆球半径,是使L偏小,使g偏小,B错误;
C.将n次全振动记为(n-1)次全振动,则T的测量值偏大,使g偏小,C错误;
D.将n次全振动记为(n+1)次全振动,T的测量值偏小,使g偏大,D正确。
故选D。
3.B
【解析】
AC.摆线过长、摆角过小、质量过大对测量结果都没有影响,故AC错误;
BD.根据
得
可知在测量摆长时,将线长和小球直径之和作为了摆长,偏大,偏大;测量周期时,时间t内全振动次数少数了一次,则周期偏大,偏小。故B正确,D错误。
故选B。
4.D
【解析】
A.研究匀变速直线运动,需要打点计时器和纸带来测物体运动的速度和加速度,所以A错误;
B.验证牛顿运动定律,需要打点计时器和纸带来测物体运动的加速度,所以B错误;
C.探究动能定理,需要打点计时器和纸带来测物体运动的速度,所以C错误;
D.用单摆测定重力加速度,不需要打点计时器,使用秒表计时,所以D正确。
故选D。
5.BCE
【解析】
A.单摆在摆角小于5°时的运动是简谐运动,单摆的摆角不能太大,A错误;
B.为减小空气阻力对实验的影响,应选体积较小、质量较大的摆球,B正确;
C.为减小周期测量误差,测量周期时,应取摆球通过最低点做为计时的起、终点位置,C正确;
D.图像不通过坐标原点,从图像可以得到相同的周期下,摆长偏小,故可能是漏加小球半径,D错误;
E.根据
则
解得
E正确。
故选BCE。
6.BDE
【解析】
由单摆的周期公式得
A.数振动次数时,少计了一次,则求出的周期T偏大,由知测量值偏小,则A错误;
B.数振动次数时,多计了一次,则求出的周期T偏小,由知测量值偏大,则B正确;
C.振动中出现松动,使摆线变长,测得的周期变大,则由可知测量值偏小,C错误;
D.测量摆长时,将细线的长度加上小球的直径作为摆长,则由可知测量值偏大,则D正确;
E.形成圆锥摆,如图所示:
根据向心力计算公式可得
解得
则周期偏小,g测量值偏大,则E正确;
故选BDE。
7.AC
【解析】
A.在制作单摆时,摆球直径要尽量远远小于摆线长,摆球质量的选择应远远大于摆线质量,这样才能接近单摆的理想条件,A正确;
B.摆长为悬点到球心的距离,即摆长等于摆线长加小球半径,B错误;
C.要保证单摆做简谐运动,摆角要小于5 ,C正确;
D.实验中为减小误差,测周期时一般需要测出单摆完成n次全振动需要的时间t,然后求出周期,故D错误.
故选AC.
8. ACF B 2.29 2.075 1.00
【解析】
【详解】
(1)AB.为了减小误差,摆线应选择尽量长些的,故A符合题意,B不符合题意;
CD.为了减小空气阻力对实验的影响,摆球应选择密度较大的钢球,故C符合题意,D不符合题意;
EF.实验中需要测量细线的长度,为了能够更加精确,应选择最小刻度为1mm的直尺,故E不符合题意,F符合题意。
故选ACF.
(2)当摆球运动至最低点时速度最大,以此作为计时标记位置对时间的测量相对误差最小,故选B。
(3)秒表读数为
该单摆的周期为
(4)摆球的直径为
摆线长为
所以单摆的摆长为
(5)根据单摆周期公式
可得
9. 0.8034 平衡位置 摆长的测量值偏小或周期的测量值偏大
【解析】
【详解】
(1)如图所示
可知刻度尺的读数为80.97cm,游标卡尺的读数为12.6mm,故小球的半径为6.3mm,故摆长为
(2)由于实际摆动过程最高点的位置会发生变化,且在最高点附近速度较小,为减小误差,步骤c中的计时起点为小球运动到平衡位置。
(3)单摆的周期公式为
整理得
由图线的斜率可得
解得
(4)若查询所在地的重力加速度g=9.797m/s2,可知测量值偏小,由周期公式可得
故可能的原因是:摆长的测量值偏小或周期的测量值偏大。
10. 12.5 C
【解析】
【详解】
(1)小球的直径为
(2) A.为减少误差应选用密度较大、体积较小的小球,A错误;
B.应记录摆球完成次全振动的时间,再计算周期,B错误;
C.选用的细线应细、质量小,且不易伸长,C正确;
D.计时起点应从摆球经过最低点时开始计时,D错误。
故选C。
(3)据单摆周期公式可得
整理得
可知,图线的斜率为
故重力加速度的表达式为
当时,,可知纵轴截距的绝对值是小球的半径。
11. D 9.76 D
【解析】
(1)单摆摆动过程中,摆线要求长度不变,摆线应该选择弹性小的细线,且摆球应选择密度大的铁球,以减小阻力的影响,故选D;
(2)根据单摆周期公式
有
而T2=4.04l+0.05,从方程中可知
解得
从方程中可知T2与l没有成正比,说明l等于0,周期不为0,即可能忘了加小球半径,与小球的计时位置,及小球摆角均无关;故选D。
12. 9.76 B
【解析】
【详解】
(1)摆长
周期
则由公式
可得
(2)A.测摆线长时摆线拉得过紧,会使摆长的测量值偏大,则g测量值偏大,A错误;
B.由公式
知当实际摆长变长时,实际的周期就变大,那么测量的加速度就变小,B正确;
C.开始计时时,秒表过迟按下,会使周期T的测量值偏小,则g测量值偏大,C错误;
D.实验中误将49次全振动计为50次,会使周期T的测量值偏小,则g测量值偏大,D错误。
故选B。
(3)把公式
变为
易知斜率
则
13. 2.18 C
【解析】
【详解】
(1)游标卡尺读数是主尺读数(mm的整数位)加上游标尺读数(mm的小数位),由甲图可读出游标卡尺读数为。
(2)AB.由单摆周期公式得
周期测量值
可知重力加速度测量值偏大与摆球质量、振幅(不能太大)无关;AB错误;
D.单摆的悬点为固定,导致摆长变大,但是数据处理仍旧按照原来的摆长来计算加速度则测量值偏小,D错误;
C.将n次摆动当成(n+1)次则周期变小,因此测量值偏大,C正确;
故选C。
(3)由可得
则图像的斜率
得
14. 147
【解析】
单摆的摆长
由单摆的周期公式
可得
地球上标准钟秒针转一周用时,则在月球上
15. 29.8mm 99.8s
【解析】
【详解】
图甲所示游标卡尺主尺的示数是29mm,游标尺的示数是8×0.1mm=0.8mm,
小球的直径d=29mm+0.8mm=29.8mm;
图乙所示秒表分针示数是1.5min,秒针示数是9.8s,秒表所示是90s+9.8s=99.8s
16.
【解析】
设A到铁锁重心的距离为l,则第1、2次的摆长分别为l+l1、l+l2,由
T1=2π
T2=2π
联立解得
g=
17. B
【解析】
根据单摆的周期公式可得
根据图甲可知
即
因为从赤道到两级重力加速度变大,故在北大的斜率小,因此是B;
由图乙可知
两摆的摆长之比等于周期的平方比,由
,
可得摆长比为。
试卷第页,共页
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
