苏教版 数学六年级下册 第4单元比例常考题型归类(无答案)
文档属性
| 名称 | 苏教版 数学六年级下册 第4单元比例常考题型归类(无答案) | 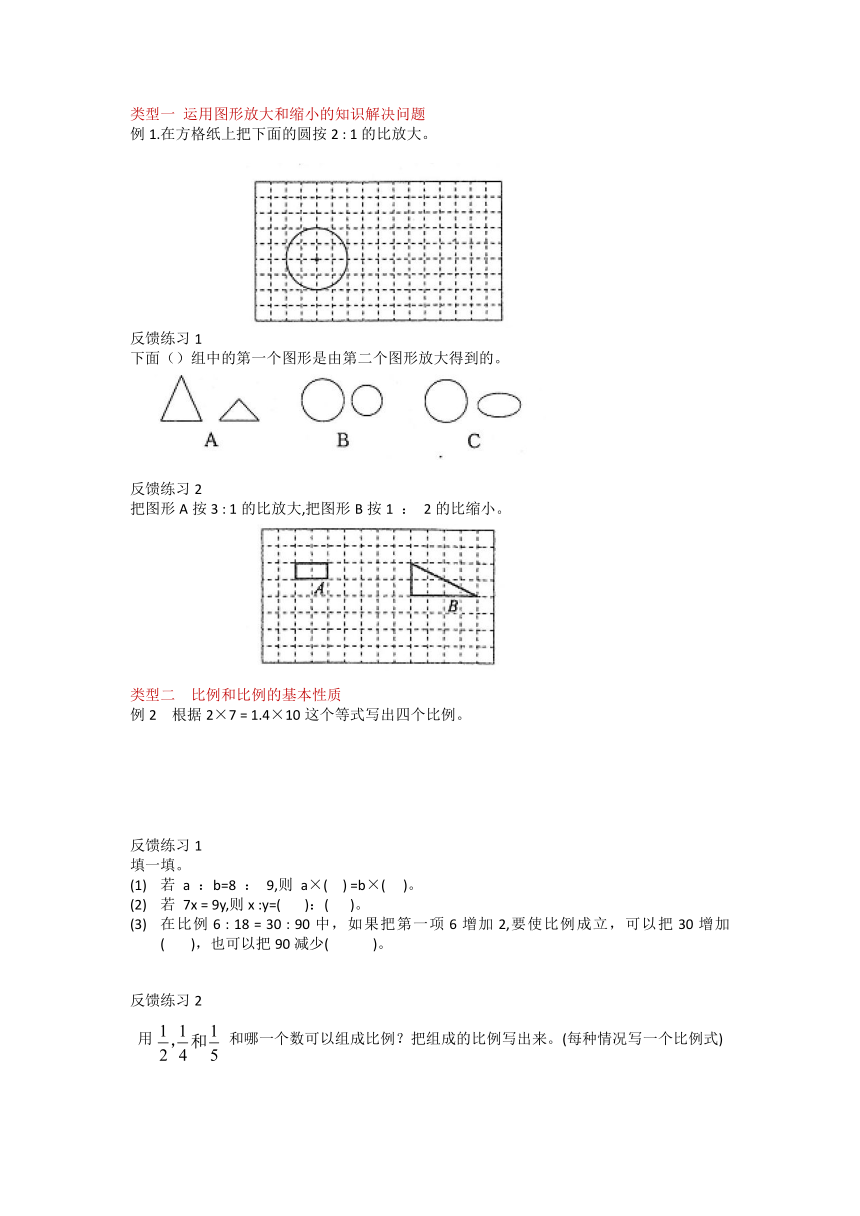 | |
| 格式 | zip | ||
| 文件大小 | 83.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 21:19:18 | ||
图片预览


文档简介
类型一 运用图形放大和缩小的知识解决问题
例1.在方格纸上把下面的圆按2 : 1的比放大。
反馈练习1
下面()组中的第一个图形是由第二个图形放大得到的。
反馈练习2
把图形A按3 : 1的比放大,把图形B按1 : 2的比缩小。
类型二 比例和比例的基本性质
例2 根据2×7 = 1.4×10这个等式写出四个比例。
反馈练习1
填一填。
(1) 若 a :b=8 : 9,则 a×( ) =b×( )。
(2) 若 7x = 9y,则x :y=( ):( )。
(3) 在比例6 : 18 = 30 : 90中,如果把第一项6增加2,要使比例成立,可以把30增加 ( ),也可以把90减少( )。
反馈练习2
用 和哪一个数可以组成比例?把组成的比例写出来。(每种情况写一个比例式)
类型三 比例尺
例3 一幅地图,图上距离20厘米表示实际距离10千米。求这幅地图的比例尺。
反馈练习1
选一选。
(1)选择合适的比例尺的字母填在括号里。
① 图上距离是实际距离的四百万分之一。 ( )
② 图上1厘米表示实际4000米。 ( )
③ 实际距离是图上距离的4000倍。 ( )
④ ( )
A. 1 : 400000 B. 1 : 4000000
C. 1 : 4000 D. 1 : 40000000
(2)有一张边长7分米的正方形纸,要在上面画长120米、宽90米的长方形操场平面
图,以下比例尺中,较合适的是( )。
A. 1 : 15 B. 1 : 20
C. 1 : 150 D. 1 : 200
反馈练习2
第31届夏季奥林匹克运动会的开幕式在巴西里约热内卢的马拉卡纳体育场举行。这个体育场的草坪长是110米,它在一幅图纸上的长是22厘米,这幅图纸的比例尺是多少?
类型四 比例尺的实际应用
例4 一幅地图的比例尺是1 : 60000,现在改用1 : 50000的比例尺重新绘制,原地图中
5厘米的距离,在新地图中应该画多少厘米?
反馈练习1
甲、乙两地相距140千米,在一幅地图上量得甲、乙之间的长度为35厘米,同时量得乙、丙之间的长度为16厘米。乙、丙两地之间的实际距离是多少千米?
反馈练习2
在比例尺是1 : 2000000的地图上,量得A、B两地之间的距离是3.6厘米。王叔叔上午8时开车从A地前往B地,平均每小时行驶48千米,那么他什么时间到达B地?
类型五 巧用比例解决问题
例5.教院附小组织了一次春游,参加春游的女生人数的 与男生人数的 相等,男生比女生 少2人。参加春游的男生和女生各有多少人?
反馈练习1
一个服装厂生产了一批夏装,已知女装数量的 等于男装数量的 ,男装比女装少150件。这批夏装中男装和女装各有多少件?
反馈练习2
一个玻璃瓶内装有盐水,原来盐的质量占水质量的 ,加入15克盐后,盐的质量占盐水质
量的 。玻璃瓶内原有盐水多少克?
类型六 图形的放大与缩小
例6. 在一幅比例尺是50 : 1的精密零件图上,量得一个半圆形零件的直径是8厘米。这个精密零件的实际面积是多少平方毫米?
反馈练习1
把一个长方体的棱长按3 : 1的比放大,那么放大后与放大前长方体表面积的比是( )。如果放大后长方体的体积是810立方分米,那么放大前长方体的体积是( )立方分米。
反馈练习2
在一幅比例尺是1 : 1000的地图上,量得小区广场上一个等腰直角三角形花坛的直角边长是3厘米,现在要贴着花坛底面铺一层营养土。如果每平方米需要5千克营养土,那么这个花坛需要多少吨营养土?
综合练习
1.把一个正方形按1 : 3的比放大,放大后正方形的边长扩大到原来的3 倍。 ( )
2. 根据要求写出比例。比例的两个内项都是5,且比值都是5。( )
3.在比例尺是1 : 6000000的地图上,量得两地间的距离是4厘米。甲、乙两辆汽车同时从两地相向而行,3小时后相遇。甲、乙两车的速度比是2 : 3,甲、乙两车每小时各行多少千米?
在一个比例中,两个比的比值都等于2,两个内项分别是 和 ,这个比例是( )。
例1.在方格纸上把下面的圆按2 : 1的比放大。
反馈练习1
下面()组中的第一个图形是由第二个图形放大得到的。
反馈练习2
把图形A按3 : 1的比放大,把图形B按1 : 2的比缩小。
类型二 比例和比例的基本性质
例2 根据2×7 = 1.4×10这个等式写出四个比例。
反馈练习1
填一填。
(1) 若 a :b=8 : 9,则 a×( ) =b×( )。
(2) 若 7x = 9y,则x :y=( ):( )。
(3) 在比例6 : 18 = 30 : 90中,如果把第一项6增加2,要使比例成立,可以把30增加 ( ),也可以把90减少( )。
反馈练习2
用 和哪一个数可以组成比例?把组成的比例写出来。(每种情况写一个比例式)
类型三 比例尺
例3 一幅地图,图上距离20厘米表示实际距离10千米。求这幅地图的比例尺。
反馈练习1
选一选。
(1)选择合适的比例尺的字母填在括号里。
① 图上距离是实际距离的四百万分之一。 ( )
② 图上1厘米表示实际4000米。 ( )
③ 实际距离是图上距离的4000倍。 ( )
④ ( )
A. 1 : 400000 B. 1 : 4000000
C. 1 : 4000 D. 1 : 40000000
(2)有一张边长7分米的正方形纸,要在上面画长120米、宽90米的长方形操场平面
图,以下比例尺中,较合适的是( )。
A. 1 : 15 B. 1 : 20
C. 1 : 150 D. 1 : 200
反馈练习2
第31届夏季奥林匹克运动会的开幕式在巴西里约热内卢的马拉卡纳体育场举行。这个体育场的草坪长是110米,它在一幅图纸上的长是22厘米,这幅图纸的比例尺是多少?
类型四 比例尺的实际应用
例4 一幅地图的比例尺是1 : 60000,现在改用1 : 50000的比例尺重新绘制,原地图中
5厘米的距离,在新地图中应该画多少厘米?
反馈练习1
甲、乙两地相距140千米,在一幅地图上量得甲、乙之间的长度为35厘米,同时量得乙、丙之间的长度为16厘米。乙、丙两地之间的实际距离是多少千米?
反馈练习2
在比例尺是1 : 2000000的地图上,量得A、B两地之间的距离是3.6厘米。王叔叔上午8时开车从A地前往B地,平均每小时行驶48千米,那么他什么时间到达B地?
类型五 巧用比例解决问题
例5.教院附小组织了一次春游,参加春游的女生人数的 与男生人数的 相等,男生比女生 少2人。参加春游的男生和女生各有多少人?
反馈练习1
一个服装厂生产了一批夏装,已知女装数量的 等于男装数量的 ,男装比女装少150件。这批夏装中男装和女装各有多少件?
反馈练习2
一个玻璃瓶内装有盐水,原来盐的质量占水质量的 ,加入15克盐后,盐的质量占盐水质
量的 。玻璃瓶内原有盐水多少克?
类型六 图形的放大与缩小
例6. 在一幅比例尺是50 : 1的精密零件图上,量得一个半圆形零件的直径是8厘米。这个精密零件的实际面积是多少平方毫米?
反馈练习1
把一个长方体的棱长按3 : 1的比放大,那么放大后与放大前长方体表面积的比是( )。如果放大后长方体的体积是810立方分米,那么放大前长方体的体积是( )立方分米。
反馈练习2
在一幅比例尺是1 : 1000的地图上,量得小区广场上一个等腰直角三角形花坛的直角边长是3厘米,现在要贴着花坛底面铺一层营养土。如果每平方米需要5千克营养土,那么这个花坛需要多少吨营养土?
综合练习
1.把一个正方形按1 : 3的比放大,放大后正方形的边长扩大到原来的3 倍。 ( )
2. 根据要求写出比例。比例的两个内项都是5,且比值都是5。( )
3.在比例尺是1 : 6000000的地图上,量得两地间的距离是4厘米。甲、乙两辆汽车同时从两地相向而行,3小时后相遇。甲、乙两车的速度比是2 : 3,甲、乙两车每小时各行多少千米?
在一个比例中,两个比的比值都等于2,两个内项分别是 和 ,这个比例是( )。
