2021-2022学年苏科版七年级数学下7.1 探索两直线平行的条件 同步强化训练(一)(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下7.1 探索两直线平行的条件 同步强化训练(一)(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 405.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 13:09:59 | ||
图片预览




文档简介
2021-2022学年苏科版七年级数学下《7.1 探索两直线平行的条件》同步强化训练(一)
(时间:60分钟 满分:120分)
一.选择题(每小题2分 共36分)
1.下列图形中,∠1与∠2是同位角的是( )
A B C D
2.下列图形中,已知∠1=∠2,则可得到AB∥CD的是( )
第2题图 第3题图 第4题图
3.如图直线AB,AF被BC所截,则∠2的同位角是( )
A.∠1 B.∠3 C.∠4 D.∠A
4.如图,∠1=120°,要使a∥b,则∠2的度数是( )
A.60° B.80° C.100° D.120°
5.下面四个图形中,∠1和∠2是同位角的是( )
A.②③④ B.①②③ C.①②③④ D.①②④
第5题图 第6题图 第7题图
6.如图,不能判定AB∥CD的是( )
A. ∠B=∠DCE B. ∠A=∠ACD C. ∠B+∠BCD=180° D. ∠A=∠DCE
7.如图,下列说法正确的是( )
A. 如果∠1和∠2互补,那么l1∥l2 B. 如果∠2=∠3,那么l1∥l2
C. 如果∠1=∠2,那么l1∥l2 D. 如果∠2和∠3互补,那么l1∥l2
8.如图,下面四种沿AB折叠的方法中,不一定能判定两条边线a,b互相平行的是( )
A. 如图①,展开后测得∠1=∠2 B. 如图②,展开后测得∠1=∠2且∠3=∠4
C. 如图③,测得∠1=∠2 D. 如图④,展开后测得∠1+∠2=180°
第8题图 第9题图
9.如图,下列条件中能判定直线l1∥l2的是( )
A. ∠1=∠2 B. ∠1=∠5 C. ∠1+∠3=180° D. ∠3=∠5
10.下列四个图形中,∠1和∠2是内错角的是( )
A.B.C.D.
第10题图 第11题图
11.如图,已知∠1=∠B,则下列说法正确的是( )
A. AB与CD平行 B. AC与DE平行
C. AB与CD平行,AC与DE也平行 D. 以上说法都不正确
12.图中,∠1和∠2是同位角的个数是( )
A.1个 B.2个 C.3个 D.4个
第12题图 第13题图
13.如图所示的四个图形中,∠1和∠2是内错角的是( )
A.① B.② C.③ D.④
14.如图,已知直线a,b被直线c所截,下列有关∠1与∠2说法正确的是( )
A.∠1与∠2是同位角 B.∠1与∠2是内错角
C.∠1与∠2是同旁内角 D.∠1与∠2是对顶角
第14题图 第15题图 第16题图 第17题图
15.如图,直线a、b被直线c所截,与∠1是同位角的( )
A.∠2 B.∠3 C.∠4 D.∠5
16.如图,已知∠1=30°,则下列结论正确的有( )
①若∠2=30°,则AB∥CD;②若∠5=30°,则AB∥CD;③若∠3=150°,则AB∥CD;
④若∠4=150°,则AB∥CD.
A. 1个 B. 2个 C. 3个 D. 4个
17.如图,∠1=120°.要使a∥b,则∠2的度数是( )
A. 60° B. 80° C. 100° D. 120°
18.下列说法错误的是( )
A. 同一平面内的两条直线不平行就相交 B. 同位角相等,两直线平行
C. 过直线外一点只有一条直线与已知直线平行 D. 同位角互补,两直线平行
二.填空题(第24,25,26.27题每空2分,其余每空1分 共28分)
19.如图直线AB,CD被直线EF所截,因为∠1与∠2都在直线EF的 侧,∠1在直线AB的 方,∠2在直线CD的 方,所以∠1与∠2是 角.
第19题图 第20题图 第21题图 第22题图 第23题图
20.如图,∠B与 是直线 和直线 被直线 所截得的同位角.
21.如图,∠1与∠2是直线 , 被直线EF所截得的同位角,且∠1=∠2,根据“ ”得AB∥CD.
22.如图,因为∠ECD=∠B,所以 ∥ , 理由是 .
23.如图在线段CD上,点F在线段AB上,G是线段AD的延长线上一点.
(1)若∠A=∠1,则可判定 ∥ ;
(2)若∠2=∠CDA,则可判定 ∥ ;
(3)若∠B=∠AFE,则可判定 ∥ .
24.如图给出了过直线外一点作已知直线的平行线的方法,其依据是 .
第24题图 第25题图 第26题图 第27题图
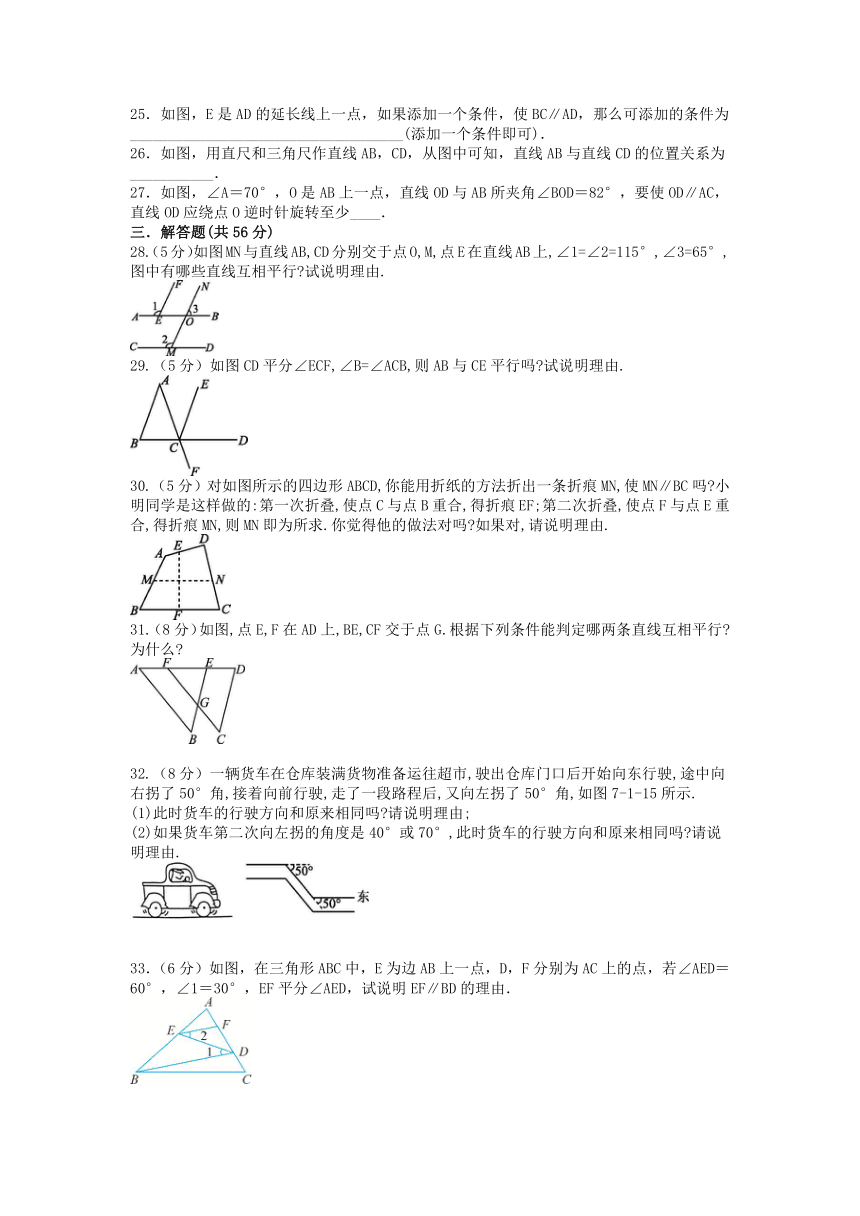
25.如图,E是AD的延长线上一点,如果添加一个条件,使BC∥AD,那么可添加的条件为____________________________________(添加一个条件即可).
26.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为___________.
27.如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD应绕点O逆时针旋转至少____.
三.解答题(共56分)
28.(5分)如图MN与直线AB,CD分别交于点O,M,点E在直线AB上,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行 试说明理由.
29.(5分)如图CD平分∠ECF,∠B=∠ACB,则AB与CE平行吗 试说明理由.
30.(5分)对如图所示的四边形ABCD,你能用折纸的方法折出一条折痕MN,使MN∥BC吗 小明同学是这样做的:第一次折叠,使点C与点B重合,得折痕EF;第二次折叠,使点F与点E重合,得折痕MN,则MN即为所求.你觉得他的做法对吗 如果对,请说明理由.
31.(8分)如图,点E,F在AD上,BE,CF交于点G.根据下列条件能判定哪两条直线互相平行 为什么
32.(8分)一辆货车在仓库装满货物准备运往超市,驶出仓库门口后开始向东行驶,途中向右拐了50°角,接着向前行驶,走了一段路程后,又向左拐了50°角,如图7-1-15所示.
(1)此时货车的行驶方向和原来相同吗 请说明理由;
(2)如果货车第二次向左拐的角度是40°或70°,此时货车的行驶方向和原来相同吗 请说明理由.
33.(6分)如图,在三角形ABC中,E为边AB上一点,D,F分别为AC上的点,若∠AED=60°,∠1=30°,EF平分∠AED,试说明EF∥BD的理由.
34.(6分)如图,∠BAF=46°,∠ACE=136°,CE⊥CD.试说明CD∥AB的理由.
35.(5分)如图,已知∠B=∠D,∠B+∠FCB=180°,试说明BE∥DG的理由.
36.(8分)(1)如图①,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由.
(2)如图②,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.
教师样卷
一.选择题(每小题2分 共36分)
1.下列图形中,∠1与∠2是同位角的是 ( A )
A B C D
2.下列图形中,已知∠1=∠2,则可得到AB∥CD的是 ( B )
第2题图 第3题图 第4题图
3.如图直线AB,AF被BC所截,则∠2的同位角是 ( C )
A.∠1 B.∠3 C.∠4 D.∠A
4.如图,∠1=120°,要使a∥b,则∠2的度数是( D )
A.60° B.80° C.100° D.120°
5.下面四个图形中,∠1和∠2是同位角的是 ( D )
A.②③④ B.①②③ C.①②③④ D.①②④
第5题图 第6题图 第7题图
6.如图,不能判定AB∥CD的是(D)
A. ∠B=∠DCE B. ∠A=∠ACD C. ∠B+∠BCD=180° D. ∠A=∠DCE
7.如图,下列说法正确的是(D)
A. 如果∠1和∠2互补,那么l1∥l2 B. 如果∠2=∠3,那么l1∥l2
C. 如果∠1=∠2,那么l1∥l2 D. 如果∠2和∠3互补,那么l1∥l2
8.如图,下面四种沿AB折叠的方法中,不一定能判定两条边线a,b互相平行的是(C)
A. 如图①,展开后测得∠1=∠2 B. 如图②,展开后测得∠1=∠2且∠3=∠4
C. 如图③,测得∠1=∠2 D. 如图④,展开后测得∠1+∠2=180°
第8题图 第9题图
9.如图,下列条件中能判定直线l1∥l2的是(C)
A. ∠1=∠2 B. ∠1=∠5 C. ∠1+∠3=180° D. ∠3=∠5
10.下列四个图形中,∠1和∠2是内错角的是( C )
A.B.C.D.
第10题图 第11题图
11.如图,已知∠1=∠B,则下列说法正确的是(A)
A. AB与CD平行 B. AC与DE平行
C. AB与CD平行,AC与DE也平行 D. 以上说法都不正确
12.图中,∠1和∠2是同位角的个数是( B )
A.1个 B.2个 C.3个 D.4个
第12题图 第13题图
13.如图所示的四个图形中,∠1和∠2是内错角的是( B )
A.① B.② C.③ D.④
14.如图,已知直线a,b被直线c所截,下列有关∠1与∠2说法正确的是( A )
A.∠1与∠2是同位角 B.∠1与∠2是内错角
C.∠1与∠2是同旁内角 D.∠1与∠2是对顶角
第14题图 第15题图 第16题图 第17题图
15.如图,直线a、b被直线c所截,与∠1是同位角的( A )
A.∠2 B.∠3 C.∠4 D.∠5
16.如图,已知∠1=30°,则下列结论正确的有(B)
①若∠2=30°,则AB∥CD;②若∠5=30°,则AB∥CD;③若∠3=150°,则AB∥CD;
④若∠4=150°,则AB∥CD.
A. 1个 B. 2个 C. 3个 D. 4个
17.如图,∠1=120°.要使a∥b,则∠2的度数是(D)
A. 60° B. 80° C. 100° D. 120°
18.下列说法错误的是(D)
A. 同一平面内的两条直线不平行就相交 B. 同位角相等,两直线平行
C. 过直线外一点只有一条直线与已知直线平行 D. 同位角互补,两直线平行
二.填空题(第24,25,26.27题每空2分,其余每空1分 共28分)
19.如图直线AB,CD被直线EF所截,因为∠1与∠2都在直线EF的 侧,∠1在直线AB的 方,∠2在直线CD的 方,所以∠1与∠2是 角.
【答案】右 上 上 同位
第19题图 第20题图 第21题图 第22题图 第23题图
20.如图,∠B与 是直线 和直线 被直线 所截得的同位角.
【答案】∠DAC BC AC DB
21.如图,∠1与∠2是直线 , 被直线EF所截得的同位角,且∠1=∠2,根据“ ”得AB∥CD.
【答案】AB CD 同位角相等,两直线平行
22.如图,因为∠ECD=∠B,所以 ∥ , 理由是 .
【答案】EC AB 同位角相等,两直线平行
23.如图在线段CD上,点F在线段AB上,G是线段AD的延长线上一点.
(1)若∠A=∠1,则可判定 ∥ ;
(2)若∠2=∠CDA,则可判定 ∥ ;
(3)若∠B=∠AFE,则可判定 ∥ .
【答案】(1)AB CD (2)EF AD (3)BC EF [解析] (1)因为∠A=∠1,根据“同位角相等,两直线平行”,可得AB∥CD;(2)因为∠2=∠CDA,根据“同位角相等,两直线平行”,可得EF∥AD;(3)因为∠B=∠AFE,根据“同位角相等,两直线平行”,可得BC∥EF.
24.如图给出了过直线外一点作已知直线的平行线的方法,其依据是 .
【答案】同位角相等,两直线平行
第24题图 第25题图 第26题图 第27题图
25.如图,E是AD的延长线上一点,如果添加一个条件,使BC∥AD,那么可添加的条件为____________________________________(添加一个条件即可).
【答案】∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE(
26.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为___________.
【答案】平行
27.如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD应绕点O逆时针旋转至少____.
【答案】_12°
三.解答题(共56分)
28.(5分)如图MN与直线AB,CD分别交于点O,M,点E在直线AB上,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行 试说明理由.
解:EF∥MN,AB∥CD. 理由:由∠3=65°,可得到∠AON=115°,从而∠1=∠2=∠AON=115°,再根据“同位角相等,两直线平行”,得到EF∥MN,AB∥CD.
29.(5分)如图CD平分∠ECF,∠B=∠ACB,则AB与CE平行吗 试说明理由.
解:AB∥CE.理由:因为CD平分∠ECF,所以∠ECD=∠DCF.因为∠ACB=∠DCF,所以∠ECD=∠ACB.又因为∠B=∠ACB,所以∠B=∠ECD,所以AB∥CE.
30.(5分)对如图所示的四边形ABCD,你能用折纸的方法折出一条折痕MN,使MN∥BC吗 小明同学是这样做的:第一次折叠,使点C与点B重合,得折痕EF;第二次折叠,使点F与点E重合,得折痕MN,则MN即为所求.你觉得他的做法对吗 如果对,请说明理由.
解:他的做法是对的.理由:设EF与MN交于点O,由两次折叠可知∠EON=∠EFC=90°,根据“同位角相等,两直线平行”,可得MN∥BC.
31.(8分)如图,点E,F在AD上,BE,CF交于点G.根据下列条件能判定哪两条直线互相平行 为什么
解:(1)BE∥CD.理由:因为∠AEB=∠D,根据“同位角相等,两直线平行”,可得BE∥CD.
(2)CF∥AB.理由:因为∠EGF=∠B,根据“同位角相等,两直线平行”,可得CF∥AB.
(3)CF∥AB.理由:因为∠DFG=∠A,根据“同位角相等,两直线平行”,可得CF∥AB.
(4)BE∥CD.理由:因为∠EGF=∠C,根据“同位角相等,两直线平行”,可得BE∥CD.
32.(8分)一辆货车在仓库装满货物准备运往超市,驶出仓库门口后开始向东行驶,途中向右拐了50°角,接着向前行驶,走了一段路程后,又向左拐了50°角,如图7-1-15所示.
(1)此时货车的行驶方向和原来相同吗 请说明理由;
(2)如果货车第二次向左拐的角度是40°或70°,此时货车的行驶方向和原来相同吗 请说明理由.
解:(1)货车的行驶方向和原来相同.理由如下:
如图,因为∠AOO'=∠A'O'B'=50°,根据“同位角相等,两直线平行”可得OA∥O'A',所以货车的行驶方向和原来相同.
(2)货车的行驶方向和原来不相同.理由如下: 因为第二次向左拐的角度是40°或70°,不是50°,即同位角不相等,所以两直线不平行,即O'A'不平行于OA,所以货车的行驶方向和原来不相同.
33.(6分)如图,在三角形ABC中,E为边AB上一点,D,F分别为AC上的点,若∠AED=60°,∠1=30°,EF平分∠AED,试说明EF∥BD的理由.
【解】 ∵∠AED=60°,EF平分∠AED,∴∠2=30°(角平分线的定义).
又∵∠1=30°,∴∠1=∠2,∴EF∥BD(内错角相等,两直线平行).
34.(6分)如图,∠BAF=46°,∠ACE=136°,CE⊥CD.试说明CD∥AB的理由.
【解】 ∵CE⊥CD,∴∠DCE=90°(垂直的定义).又∵∠ACE=136°,∴∠ACD=360°-136°-90°=134°.∵∠BAF=46°,∴∠BAC=180°-∠BAF=180°-46°=134°,∴∠ACD=∠BAC,∴CD∥AB(内错角相等,两直线平行).
35.(5分)如图,已知∠B=∠D,∠B+∠FCB=180°,试说明BE∥DG的理由.
【解】 ∵∠B=∠D,∠B+∠FCB=180°,∴∠D+∠FCB=180°.∵∠ECD=∠FCB,
∴∠D+∠ECD=180°,∴BE∥DG(同旁内角互补,两直线平行).
36.(8分)(1)如图①,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由.
(2)如图②,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.
【解】 (1)AB∥CD.理由如下:∵AB⊥EF,CD⊥EF,
∴AB∥CD(在同一平面内,垂直于同一条直线的两条直线互相平行).
(2)如解图,延长NO′交AB于点P.
∵OM平分∠EOB,O′N平分∠CO′F,∠EOB=∠CO′F=90°,
∴∠EOM=∠FO′N=45°.
又∵∠FO′N=∠EO′P,∴∠EOM=∠EO′P,
∴OM∥O′P,即OM∥O′N(同位角相等,两直线平行).
(时间:60分钟 满分:120分)
一.选择题(每小题2分 共36分)
1.下列图形中,∠1与∠2是同位角的是( )
A B C D
2.下列图形中,已知∠1=∠2,则可得到AB∥CD的是( )
第2题图 第3题图 第4题图
3.如图直线AB,AF被BC所截,则∠2的同位角是( )
A.∠1 B.∠3 C.∠4 D.∠A
4.如图,∠1=120°,要使a∥b,则∠2的度数是( )
A.60° B.80° C.100° D.120°
5.下面四个图形中,∠1和∠2是同位角的是( )
A.②③④ B.①②③ C.①②③④ D.①②④
第5题图 第6题图 第7题图
6.如图,不能判定AB∥CD的是( )
A. ∠B=∠DCE B. ∠A=∠ACD C. ∠B+∠BCD=180° D. ∠A=∠DCE
7.如图,下列说法正确的是( )
A. 如果∠1和∠2互补,那么l1∥l2 B. 如果∠2=∠3,那么l1∥l2
C. 如果∠1=∠2,那么l1∥l2 D. 如果∠2和∠3互补,那么l1∥l2
8.如图,下面四种沿AB折叠的方法中,不一定能判定两条边线a,b互相平行的是( )
A. 如图①,展开后测得∠1=∠2 B. 如图②,展开后测得∠1=∠2且∠3=∠4
C. 如图③,测得∠1=∠2 D. 如图④,展开后测得∠1+∠2=180°
第8题图 第9题图
9.如图,下列条件中能判定直线l1∥l2的是( )
A. ∠1=∠2 B. ∠1=∠5 C. ∠1+∠3=180° D. ∠3=∠5
10.下列四个图形中,∠1和∠2是内错角的是( )
A.B.C.D.
第10题图 第11题图
11.如图,已知∠1=∠B,则下列说法正确的是( )
A. AB与CD平行 B. AC与DE平行
C. AB与CD平行,AC与DE也平行 D. 以上说法都不正确
12.图中,∠1和∠2是同位角的个数是( )
A.1个 B.2个 C.3个 D.4个
第12题图 第13题图
13.如图所示的四个图形中,∠1和∠2是内错角的是( )
A.① B.② C.③ D.④
14.如图,已知直线a,b被直线c所截,下列有关∠1与∠2说法正确的是( )
A.∠1与∠2是同位角 B.∠1与∠2是内错角
C.∠1与∠2是同旁内角 D.∠1与∠2是对顶角
第14题图 第15题图 第16题图 第17题图
15.如图,直线a、b被直线c所截,与∠1是同位角的( )
A.∠2 B.∠3 C.∠4 D.∠5
16.如图,已知∠1=30°,则下列结论正确的有( )
①若∠2=30°,则AB∥CD;②若∠5=30°,则AB∥CD;③若∠3=150°,则AB∥CD;
④若∠4=150°,则AB∥CD.
A. 1个 B. 2个 C. 3个 D. 4个
17.如图,∠1=120°.要使a∥b,则∠2的度数是( )
A. 60° B. 80° C. 100° D. 120°
18.下列说法错误的是( )
A. 同一平面内的两条直线不平行就相交 B. 同位角相等,两直线平行
C. 过直线外一点只有一条直线与已知直线平行 D. 同位角互补,两直线平行
二.填空题(第24,25,26.27题每空2分,其余每空1分 共28分)
19.如图直线AB,CD被直线EF所截,因为∠1与∠2都在直线EF的 侧,∠1在直线AB的 方,∠2在直线CD的 方,所以∠1与∠2是 角.
第19题图 第20题图 第21题图 第22题图 第23题图
20.如图,∠B与 是直线 和直线 被直线 所截得的同位角.
21.如图,∠1与∠2是直线 , 被直线EF所截得的同位角,且∠1=∠2,根据“ ”得AB∥CD.
22.如图,因为∠ECD=∠B,所以 ∥ , 理由是 .
23.如图在线段CD上,点F在线段AB上,G是线段AD的延长线上一点.
(1)若∠A=∠1,则可判定 ∥ ;
(2)若∠2=∠CDA,则可判定 ∥ ;
(3)若∠B=∠AFE,则可判定 ∥ .
24.如图给出了过直线外一点作已知直线的平行线的方法,其依据是 .
第24题图 第25题图 第26题图 第27题图
25.如图,E是AD的延长线上一点,如果添加一个条件,使BC∥AD,那么可添加的条件为____________________________________(添加一个条件即可).
26.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为___________.
27.如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD应绕点O逆时针旋转至少____.
三.解答题(共56分)
28.(5分)如图MN与直线AB,CD分别交于点O,M,点E在直线AB上,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行 试说明理由.
29.(5分)如图CD平分∠ECF,∠B=∠ACB,则AB与CE平行吗 试说明理由.
30.(5分)对如图所示的四边形ABCD,你能用折纸的方法折出一条折痕MN,使MN∥BC吗 小明同学是这样做的:第一次折叠,使点C与点B重合,得折痕EF;第二次折叠,使点F与点E重合,得折痕MN,则MN即为所求.你觉得他的做法对吗 如果对,请说明理由.
31.(8分)如图,点E,F在AD上,BE,CF交于点G.根据下列条件能判定哪两条直线互相平行 为什么
32.(8分)一辆货车在仓库装满货物准备运往超市,驶出仓库门口后开始向东行驶,途中向右拐了50°角,接着向前行驶,走了一段路程后,又向左拐了50°角,如图7-1-15所示.
(1)此时货车的行驶方向和原来相同吗 请说明理由;
(2)如果货车第二次向左拐的角度是40°或70°,此时货车的行驶方向和原来相同吗 请说明理由.
33.(6分)如图,在三角形ABC中,E为边AB上一点,D,F分别为AC上的点,若∠AED=60°,∠1=30°,EF平分∠AED,试说明EF∥BD的理由.
34.(6分)如图,∠BAF=46°,∠ACE=136°,CE⊥CD.试说明CD∥AB的理由.
35.(5分)如图,已知∠B=∠D,∠B+∠FCB=180°,试说明BE∥DG的理由.
36.(8分)(1)如图①,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由.
(2)如图②,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.
教师样卷
一.选择题(每小题2分 共36分)
1.下列图形中,∠1与∠2是同位角的是 ( A )
A B C D
2.下列图形中,已知∠1=∠2,则可得到AB∥CD的是 ( B )
第2题图 第3题图 第4题图
3.如图直线AB,AF被BC所截,则∠2的同位角是 ( C )
A.∠1 B.∠3 C.∠4 D.∠A
4.如图,∠1=120°,要使a∥b,则∠2的度数是( D )
A.60° B.80° C.100° D.120°
5.下面四个图形中,∠1和∠2是同位角的是 ( D )
A.②③④ B.①②③ C.①②③④ D.①②④
第5题图 第6题图 第7题图
6.如图,不能判定AB∥CD的是(D)
A. ∠B=∠DCE B. ∠A=∠ACD C. ∠B+∠BCD=180° D. ∠A=∠DCE
7.如图,下列说法正确的是(D)
A. 如果∠1和∠2互补,那么l1∥l2 B. 如果∠2=∠3,那么l1∥l2
C. 如果∠1=∠2,那么l1∥l2 D. 如果∠2和∠3互补,那么l1∥l2
8.如图,下面四种沿AB折叠的方法中,不一定能判定两条边线a,b互相平行的是(C)
A. 如图①,展开后测得∠1=∠2 B. 如图②,展开后测得∠1=∠2且∠3=∠4
C. 如图③,测得∠1=∠2 D. 如图④,展开后测得∠1+∠2=180°
第8题图 第9题图
9.如图,下列条件中能判定直线l1∥l2的是(C)
A. ∠1=∠2 B. ∠1=∠5 C. ∠1+∠3=180° D. ∠3=∠5
10.下列四个图形中,∠1和∠2是内错角的是( C )
A.B.C.D.
第10题图 第11题图
11.如图,已知∠1=∠B,则下列说法正确的是(A)
A. AB与CD平行 B. AC与DE平行
C. AB与CD平行,AC与DE也平行 D. 以上说法都不正确
12.图中,∠1和∠2是同位角的个数是( B )
A.1个 B.2个 C.3个 D.4个
第12题图 第13题图
13.如图所示的四个图形中,∠1和∠2是内错角的是( B )
A.① B.② C.③ D.④
14.如图,已知直线a,b被直线c所截,下列有关∠1与∠2说法正确的是( A )
A.∠1与∠2是同位角 B.∠1与∠2是内错角
C.∠1与∠2是同旁内角 D.∠1与∠2是对顶角
第14题图 第15题图 第16题图 第17题图
15.如图,直线a、b被直线c所截,与∠1是同位角的( A )
A.∠2 B.∠3 C.∠4 D.∠5
16.如图,已知∠1=30°,则下列结论正确的有(B)
①若∠2=30°,则AB∥CD;②若∠5=30°,则AB∥CD;③若∠3=150°,则AB∥CD;
④若∠4=150°,则AB∥CD.
A. 1个 B. 2个 C. 3个 D. 4个
17.如图,∠1=120°.要使a∥b,则∠2的度数是(D)
A. 60° B. 80° C. 100° D. 120°
18.下列说法错误的是(D)
A. 同一平面内的两条直线不平行就相交 B. 同位角相等,两直线平行
C. 过直线外一点只有一条直线与已知直线平行 D. 同位角互补,两直线平行
二.填空题(第24,25,26.27题每空2分,其余每空1分 共28分)
19.如图直线AB,CD被直线EF所截,因为∠1与∠2都在直线EF的 侧,∠1在直线AB的 方,∠2在直线CD的 方,所以∠1与∠2是 角.
【答案】右 上 上 同位
第19题图 第20题图 第21题图 第22题图 第23题图
20.如图,∠B与 是直线 和直线 被直线 所截得的同位角.
【答案】∠DAC BC AC DB
21.如图,∠1与∠2是直线 , 被直线EF所截得的同位角,且∠1=∠2,根据“ ”得AB∥CD.
【答案】AB CD 同位角相等,两直线平行
22.如图,因为∠ECD=∠B,所以 ∥ , 理由是 .
【答案】EC AB 同位角相等,两直线平行
23.如图在线段CD上,点F在线段AB上,G是线段AD的延长线上一点.
(1)若∠A=∠1,则可判定 ∥ ;
(2)若∠2=∠CDA,则可判定 ∥ ;
(3)若∠B=∠AFE,则可判定 ∥ .
【答案】(1)AB CD (2)EF AD (3)BC EF [解析] (1)因为∠A=∠1,根据“同位角相等,两直线平行”,可得AB∥CD;(2)因为∠2=∠CDA,根据“同位角相等,两直线平行”,可得EF∥AD;(3)因为∠B=∠AFE,根据“同位角相等,两直线平行”,可得BC∥EF.
24.如图给出了过直线外一点作已知直线的平行线的方法,其依据是 .
【答案】同位角相等,两直线平行
第24题图 第25题图 第26题图 第27题图
25.如图,E是AD的延长线上一点,如果添加一个条件,使BC∥AD,那么可添加的条件为____________________________________(添加一个条件即可).
【答案】∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE(
26.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为___________.
【答案】平行
27.如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD应绕点O逆时针旋转至少____.
【答案】_12°
三.解答题(共56分)
28.(5分)如图MN与直线AB,CD分别交于点O,M,点E在直线AB上,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行 试说明理由.
解:EF∥MN,AB∥CD. 理由:由∠3=65°,可得到∠AON=115°,从而∠1=∠2=∠AON=115°,再根据“同位角相等,两直线平行”,得到EF∥MN,AB∥CD.
29.(5分)如图CD平分∠ECF,∠B=∠ACB,则AB与CE平行吗 试说明理由.
解:AB∥CE.理由:因为CD平分∠ECF,所以∠ECD=∠DCF.因为∠ACB=∠DCF,所以∠ECD=∠ACB.又因为∠B=∠ACB,所以∠B=∠ECD,所以AB∥CE.
30.(5分)对如图所示的四边形ABCD,你能用折纸的方法折出一条折痕MN,使MN∥BC吗 小明同学是这样做的:第一次折叠,使点C与点B重合,得折痕EF;第二次折叠,使点F与点E重合,得折痕MN,则MN即为所求.你觉得他的做法对吗 如果对,请说明理由.
解:他的做法是对的.理由:设EF与MN交于点O,由两次折叠可知∠EON=∠EFC=90°,根据“同位角相等,两直线平行”,可得MN∥BC.
31.(8分)如图,点E,F在AD上,BE,CF交于点G.根据下列条件能判定哪两条直线互相平行 为什么
解:(1)BE∥CD.理由:因为∠AEB=∠D,根据“同位角相等,两直线平行”,可得BE∥CD.
(2)CF∥AB.理由:因为∠EGF=∠B,根据“同位角相等,两直线平行”,可得CF∥AB.
(3)CF∥AB.理由:因为∠DFG=∠A,根据“同位角相等,两直线平行”,可得CF∥AB.
(4)BE∥CD.理由:因为∠EGF=∠C,根据“同位角相等,两直线平行”,可得BE∥CD.
32.(8分)一辆货车在仓库装满货物准备运往超市,驶出仓库门口后开始向东行驶,途中向右拐了50°角,接着向前行驶,走了一段路程后,又向左拐了50°角,如图7-1-15所示.
(1)此时货车的行驶方向和原来相同吗 请说明理由;
(2)如果货车第二次向左拐的角度是40°或70°,此时货车的行驶方向和原来相同吗 请说明理由.
解:(1)货车的行驶方向和原来相同.理由如下:
如图,因为∠AOO'=∠A'O'B'=50°,根据“同位角相等,两直线平行”可得OA∥O'A',所以货车的行驶方向和原来相同.
(2)货车的行驶方向和原来不相同.理由如下: 因为第二次向左拐的角度是40°或70°,不是50°,即同位角不相等,所以两直线不平行,即O'A'不平行于OA,所以货车的行驶方向和原来不相同.
33.(6分)如图,在三角形ABC中,E为边AB上一点,D,F分别为AC上的点,若∠AED=60°,∠1=30°,EF平分∠AED,试说明EF∥BD的理由.
【解】 ∵∠AED=60°,EF平分∠AED,∴∠2=30°(角平分线的定义).
又∵∠1=30°,∴∠1=∠2,∴EF∥BD(内错角相等,两直线平行).
34.(6分)如图,∠BAF=46°,∠ACE=136°,CE⊥CD.试说明CD∥AB的理由.
【解】 ∵CE⊥CD,∴∠DCE=90°(垂直的定义).又∵∠ACE=136°,∴∠ACD=360°-136°-90°=134°.∵∠BAF=46°,∴∠BAC=180°-∠BAF=180°-46°=134°,∴∠ACD=∠BAC,∴CD∥AB(内错角相等,两直线平行).
35.(5分)如图,已知∠B=∠D,∠B+∠FCB=180°,试说明BE∥DG的理由.
【解】 ∵∠B=∠D,∠B+∠FCB=180°,∴∠D+∠FCB=180°.∵∠ECD=∠FCB,
∴∠D+∠ECD=180°,∴BE∥DG(同旁内角互补,两直线平行).
36.(8分)(1)如图①,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由.
(2)如图②,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.
【解】 (1)AB∥CD.理由如下:∵AB⊥EF,CD⊥EF,
∴AB∥CD(在同一平面内,垂直于同一条直线的两条直线互相平行).
(2)如解图,延长NO′交AB于点P.
∵OM平分∠EOB,O′N平分∠CO′F,∠EOB=∠CO′F=90°,
∴∠EOM=∠FO′N=45°.
又∵∠FO′N=∠EO′P,∴∠EOM=∠EO′P,
∴OM∥O′P,即OM∥O′N(同位角相等,两直线平行).
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
