(北师大版)八年级下册数学易错题第三章 《 图形的平移与旋转》(含答案)
文档属性
| 名称 | (北师大版)八年级下册数学易错题第三章 《 图形的平移与旋转》(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 18:01:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
(北师大版)八年级下册数学易错题
第三章 图形的平移与旋转
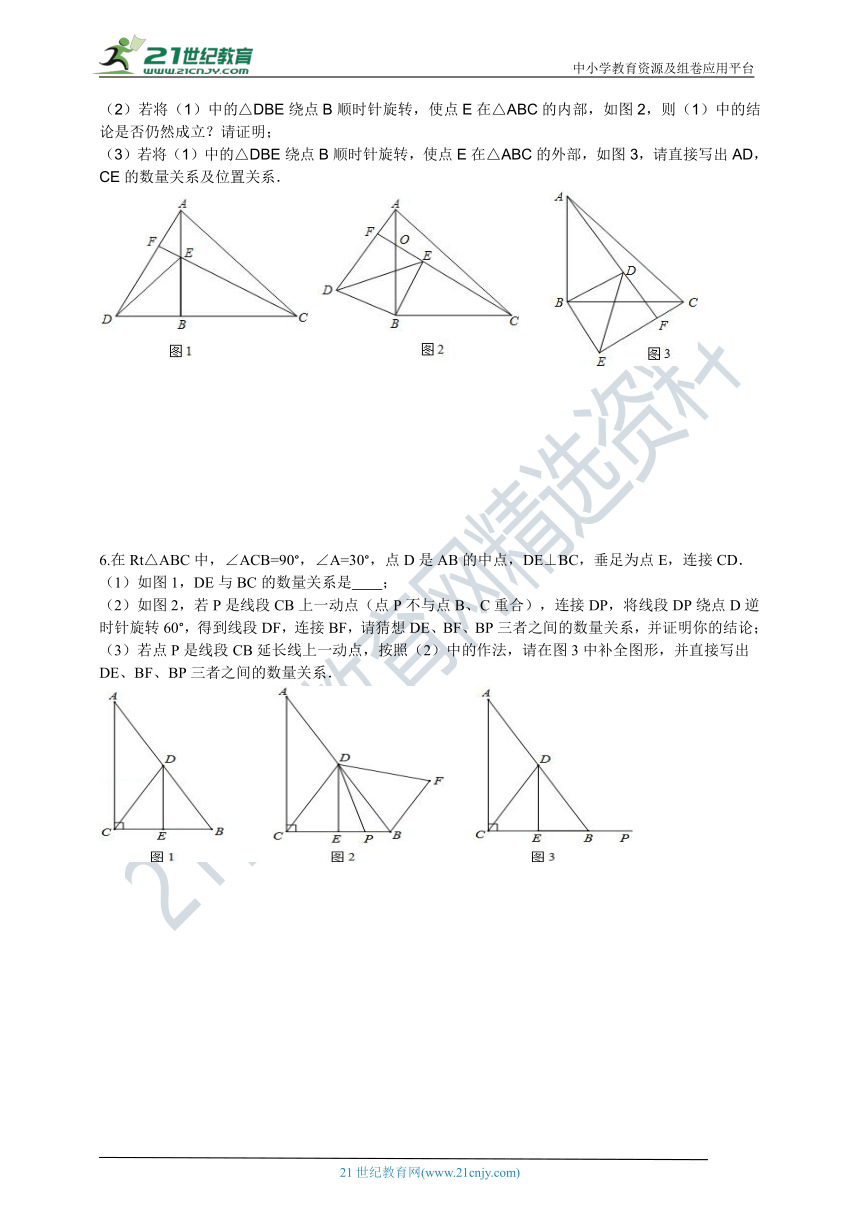
1.下列图形中,既是轴对称图形又是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
2.在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为( )
A.(1.4,-1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
3.如图所示,△DEF是由△ABC绕着某点旋转得到的,则这个点的坐标是 .
4.如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴反射得到△A2B2C2.
5.如图1,已知:Rt△ABC和Rt△DBE,∠ABC=∠DBE=90°,AB=CB,DB=EB.
(1)如图1,点D在△ABC外,点E在AB边上时,求证:AD=CE,AD⊥CE;
(2)若将(1)中的△DBE绕点B顺时针旋转,使点E在△ABC的内部,如图2,则(1)中的结论是否仍然成立?请证明;
(3)若将(1)中的△DBE绕点B顺时针旋转,使点E在△ABC的外部,如图3,请直接写出AD,CE的数量关系及位置关系.
6.在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
(北师大版)八年级下册数学易错题
参考答案及解析
第三章 图形的平移与旋转
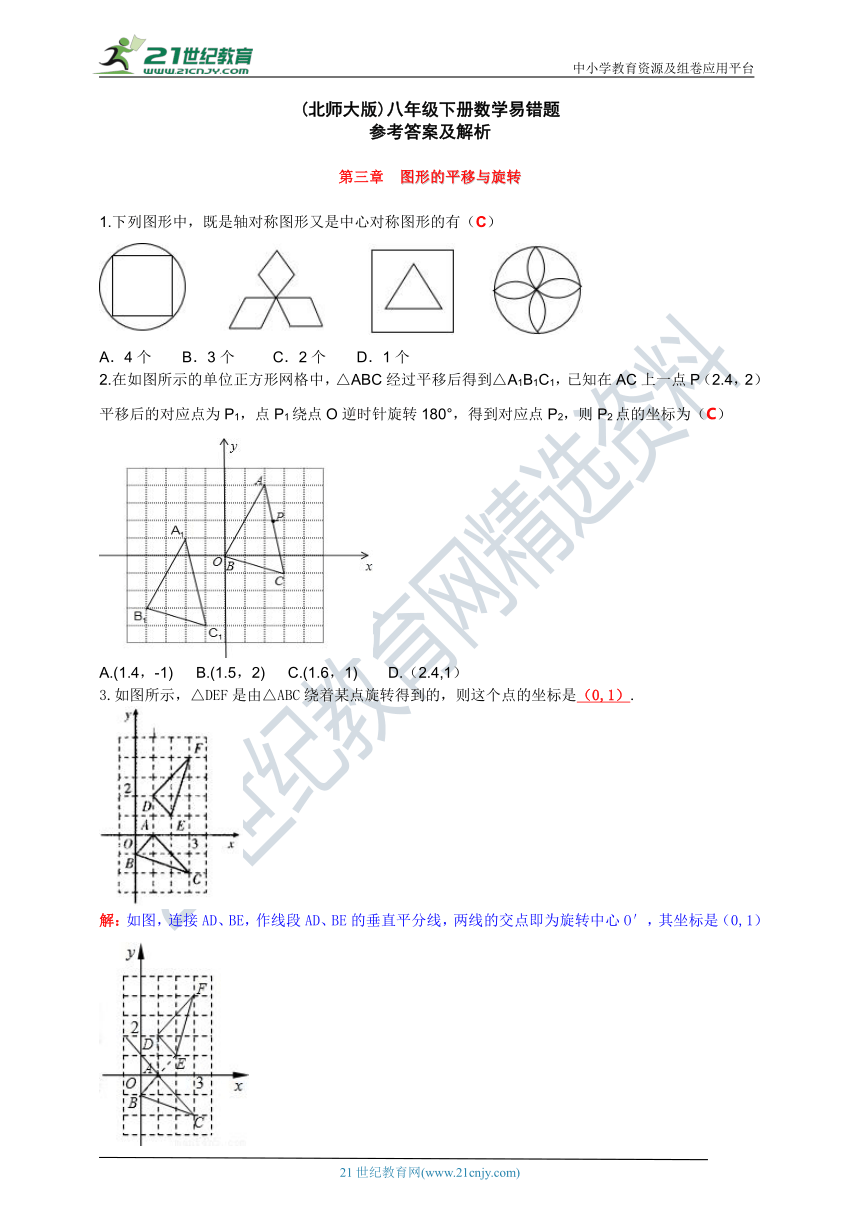
1.下列图形中,既是轴对称图形又是中心对称图形的有(C)
A.4个 B.3个 C.2个 D.1个
2.在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为(C)
A.(1.4,-1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
3.如图所示,△DEF是由△ABC绕着某点旋转得到的,则这个点的坐标是(0,1).
解:如图,连接AD、BE,作线段AD、BE的垂直平分线,两线的交点即为旋转中心O′,其坐标是(0,1)
4.如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴反射得到△A2B2C2.
5.如图1,已知:Rt△ABC和Rt△DBE,∠ABC=∠DBE=90°,AB=CB,DB=EB.
(1)如图1,点D在△ABC外,点E在AB边上时,求证:AD=CE,AD⊥CE;
(2)若将(1)中的△DBE绕点B顺时针旋转,使点E在△ABC的内部,如图2,则(1)中的结论是否仍然成立?请证明;
(3)若将(1)中的△DBE绕点B顺时针旋转,使点E在△ABC的外部,如图3,请直接写出AD,CE的数量关系及位置关系.
解:(1)证明:如图图1所示,
在△ABD和△CBE中,
∴△ABD≌△CBE(SAS)
∴AD=CE,∠BAD=∠BCE,
∵∠BCE+∠BEC=90°,∠AEF=∠BEC,
∴∠BAD+∠AEF=90°
∴∠AFE=90°
∴AD⊥CE
(2)(1)中的结论AD=CE,AD⊥CE仍然成立,理由为:
证明:如图图2所示,
∵∠ABC=∠DBE=90°
∴∠ABC-∠ABE=∠DBE-∠ABE,即∠ABD=∠CBE
在△ABD和△CBE中,
∴△ABD≌△CBE(SAS)
∴AD=CE,∠BAD=∠BCE,
∵∠BCE+∠BOC=90°,∠AOF=∠BOC,
∴∠BAD+∠AOF=90°
∴∠AFE=90°
∴AD⊥CE
(3) AD=CE,AD⊥CE,理由为:
证明:如图图3所示,设AF和BC相交于点M
∵∠ABC=∠DBE=90°
∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE
在△ABD和△CBE中,
∴△ABD≌△CBE(SAS)
∴AD=CE,∠BAD=∠BCE,
∵∠BAD+∠AMB=90°,∠AMB=∠CMF,
∴∠BCE+∠CMF=90°
∴∠AFC=90°
∴AD⊥CE
6.在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
解:(1)∵∠ACB=90°,∠A=30°
∴∠B=60°
∵点D是AB的中点,
∴DB=DC,
∴△DCB为等边三角形
∵DE⊥BC,
∴DE=BC
(2) BF+BP= DE,理由如下:
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
而∠CDB=60°
∴∠CDB-∠PDB=∠PDF-∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中
∴△DCP≌△DBF(SAS)
∴CP=BF
而CP=BC-BP
∴BF+BP=BC
∵DE=BC
∴BC=DE
∴BF+BP=DE
(3)如图,与(2)一样可证明△DCP≌△DBF
∴CP=BF
而CP=BC+BP
∴BF-BP=BC
∴BF-BP=DE
点评:本题考查了全等三角形的判断与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等,也考查了等边三角形的判断与性质以及含30度的直角三角形三边的关系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
(北师大版)八年级下册数学易错题
第三章 图形的平移与旋转
1.下列图形中,既是轴对称图形又是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
2.在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为( )
A.(1.4,-1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
3.如图所示,△DEF是由△ABC绕着某点旋转得到的,则这个点的坐标是 .
4.如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴反射得到△A2B2C2.
5.如图1,已知:Rt△ABC和Rt△DBE,∠ABC=∠DBE=90°,AB=CB,DB=EB.
(1)如图1,点D在△ABC外,点E在AB边上时,求证:AD=CE,AD⊥CE;
(2)若将(1)中的△DBE绕点B顺时针旋转,使点E在△ABC的内部,如图2,则(1)中的结论是否仍然成立?请证明;
(3)若将(1)中的△DBE绕点B顺时针旋转,使点E在△ABC的外部,如图3,请直接写出AD,CE的数量关系及位置关系.
6.在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
(北师大版)八年级下册数学易错题
参考答案及解析
第三章 图形的平移与旋转
1.下列图形中,既是轴对称图形又是中心对称图形的有(C)
A.4个 B.3个 C.2个 D.1个
2.在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为(C)
A.(1.4,-1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
3.如图所示,△DEF是由△ABC绕着某点旋转得到的,则这个点的坐标是(0,1).
解:如图,连接AD、BE,作线段AD、BE的垂直平分线,两线的交点即为旋转中心O′,其坐标是(0,1)
4.如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴反射得到△A2B2C2.
5.如图1,已知:Rt△ABC和Rt△DBE,∠ABC=∠DBE=90°,AB=CB,DB=EB.
(1)如图1,点D在△ABC外,点E在AB边上时,求证:AD=CE,AD⊥CE;
(2)若将(1)中的△DBE绕点B顺时针旋转,使点E在△ABC的内部,如图2,则(1)中的结论是否仍然成立?请证明;
(3)若将(1)中的△DBE绕点B顺时针旋转,使点E在△ABC的外部,如图3,请直接写出AD,CE的数量关系及位置关系.
解:(1)证明:如图图1所示,
在△ABD和△CBE中,
∴△ABD≌△CBE(SAS)
∴AD=CE,∠BAD=∠BCE,
∵∠BCE+∠BEC=90°,∠AEF=∠BEC,
∴∠BAD+∠AEF=90°
∴∠AFE=90°
∴AD⊥CE
(2)(1)中的结论AD=CE,AD⊥CE仍然成立,理由为:
证明:如图图2所示,
∵∠ABC=∠DBE=90°
∴∠ABC-∠ABE=∠DBE-∠ABE,即∠ABD=∠CBE
在△ABD和△CBE中,
∴△ABD≌△CBE(SAS)
∴AD=CE,∠BAD=∠BCE,
∵∠BCE+∠BOC=90°,∠AOF=∠BOC,
∴∠BAD+∠AOF=90°
∴∠AFE=90°
∴AD⊥CE
(3) AD=CE,AD⊥CE,理由为:
证明:如图图3所示,设AF和BC相交于点M
∵∠ABC=∠DBE=90°
∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE
在△ABD和△CBE中,
∴△ABD≌△CBE(SAS)
∴AD=CE,∠BAD=∠BCE,
∵∠BAD+∠AMB=90°,∠AMB=∠CMF,
∴∠BCE+∠CMF=90°
∴∠AFC=90°
∴AD⊥CE
6.在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.
解:(1)∵∠ACB=90°,∠A=30°
∴∠B=60°
∵点D是AB的中点,
∴DB=DC,
∴△DCB为等边三角形
∵DE⊥BC,
∴DE=BC
(2) BF+BP= DE,理由如下:
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
而∠CDB=60°
∴∠CDB-∠PDB=∠PDF-∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中
∴△DCP≌△DBF(SAS)
∴CP=BF
而CP=BC-BP
∴BF+BP=BC
∵DE=BC
∴BC=DE
∴BF+BP=DE
(3)如图,与(2)一样可证明△DCP≌△DBF
∴CP=BF
而CP=BC+BP
∴BF-BP=BC
∴BF-BP=DE
点评:本题考查了全等三角形的判断与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等,也考查了等边三角形的判断与性质以及含30度的直角三角形三边的关系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
