2021-2022学年人教版数学九年级下册26.1.2反比例函数的图象和性质 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册26.1.2反比例函数的图象和性质 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 776.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 09:19:33 | ||
图片预览


文档简介
(共17张PPT)
26.1.2反比例函数的
图象与性质
第一课时
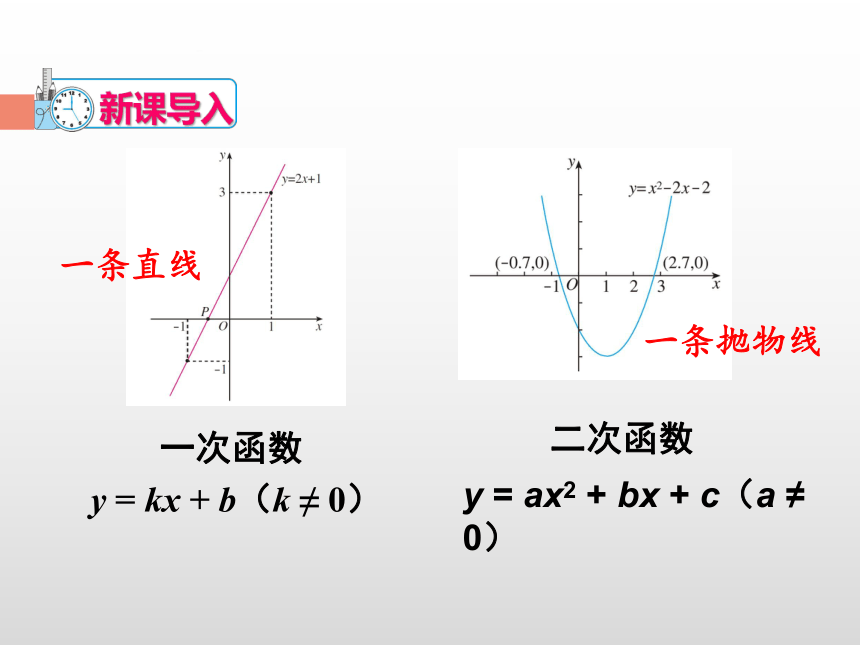
一次函数
y = kx + b(k ≠ 0)
新课导入
一条直线
二次函数
y = ax2 + bx + c(a ≠ 0)
一条抛物线
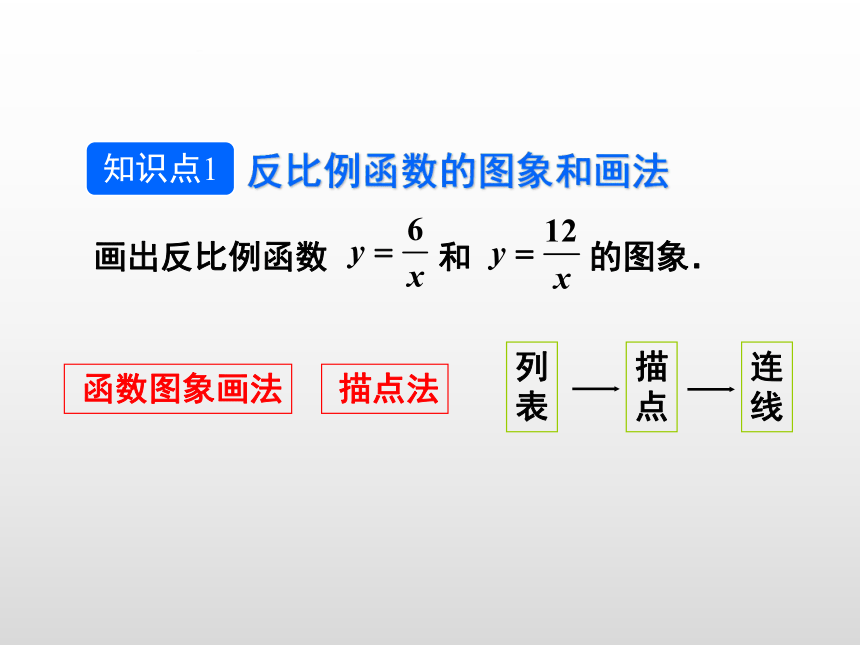
函数图象画法
列
表
描
点
连
线
描点法
画出反比例函数 和 的图象.
反比例函数的图象和画法
知识点1
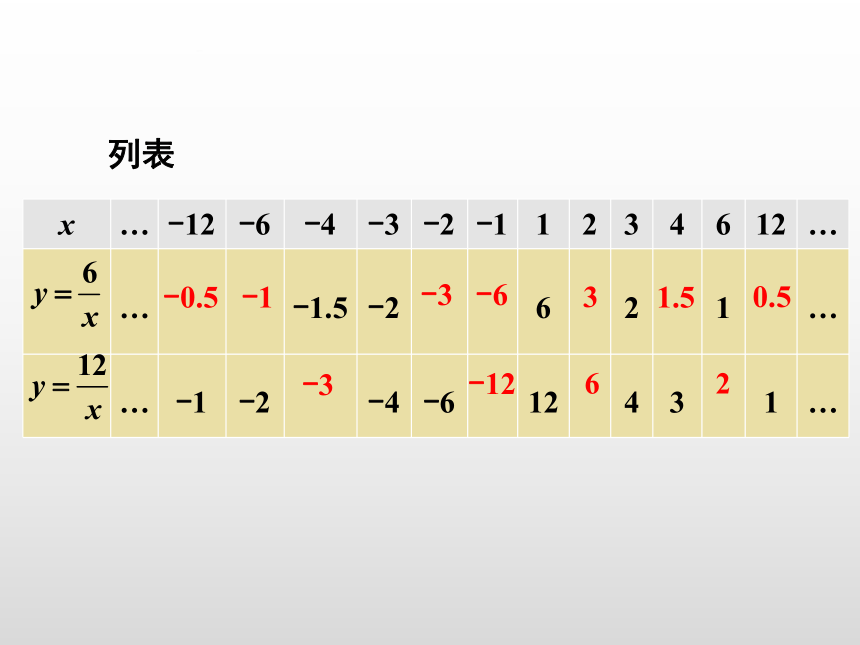
x … -12 -6 -4 -3 -2 -1 1 2 3 4 6 12 …
… -1.5 -2 6 2 1 …
… -1 -2 -4 -6 12 4 3 1 …
3
1.5
-6
-3
-1
-0.5
-12
6
-3
2
0.5
列表
5
10
x
5
10
-5
-10
-5
-10
y
O
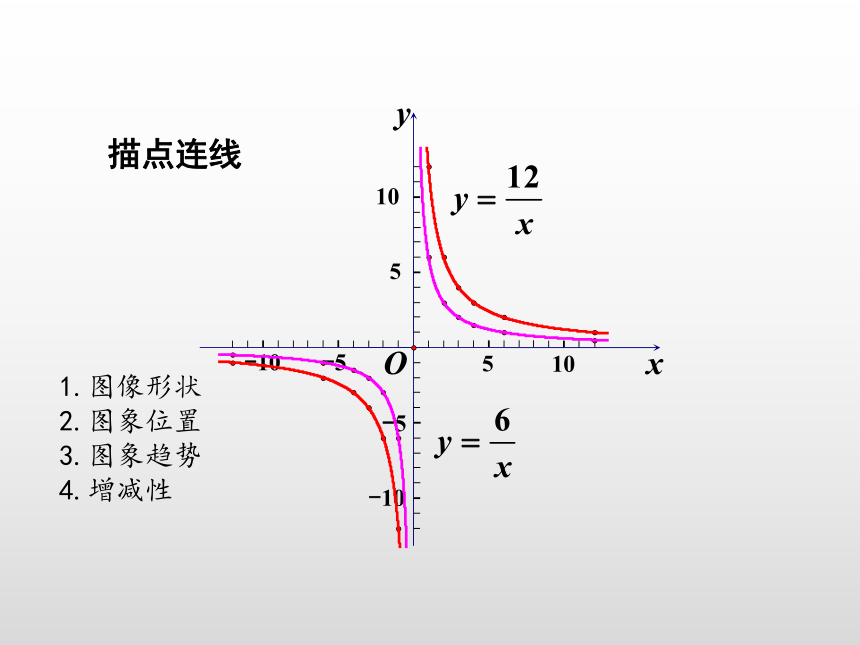
描点连线
1.图像形状
2.图象位置
3.图象趋势
4.增减性
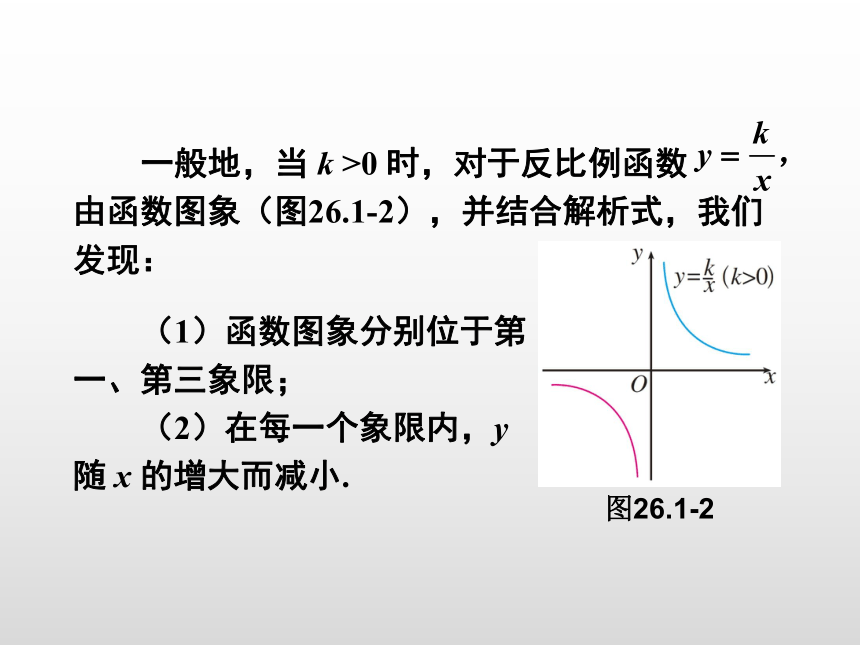
(1)函数图象分别位于第一、第三象限;
(2)在每一个象限内,y随 x 的增大而减小.
一般地,当 k >0 时,对于反比例函数 由函数图象(图26.1-2),并结合解析式,我们发现:
图26.1-2
x … -12 -6 -4 -3 -2 -1 1 2 3 4 6 12 …
… 1.5 2 -6 -2 -1 …
-3
-1.5
6
3
1
0.5
-0.5
列表
画出反比例函数 和 的图象.
画出反比例函数 的图象.
第二象限
第四象限
在每一个象限内,y随 x 的增大而增大.
难点突破
1.图像形状
2.图象位置
3.图象趋势
4.增减性
(1)函数图象分别位于第二、第四象限;
(2)在每一个象限内,y随 x 的增大而增大.
一般地,当 k <0 时,对于反比例函数 由函数图象,并结合解析式,我们发现:
归纳
(1)当 k > 0 时,函数图象分别位于第一、第三象限;在每一个象限内,y 随 x 的增大而减小.
(2)当 k < 0 时,函数图象分别位于第二、第四象限;在每一个象限内,y 随 x 的增大而增大.
一般地,反比例函数 (k≠0)的图象是双曲线,它具有以下性质:
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
一、三
二、四
减小
增大
1.下列图象中是反比例函数图象的是( )
C
A B C D
课堂演练
2.如图是下列四个函数中哪一个函数的图象( )
A. y = 5x
B. y = 2x + 3
C.
D.
C
练习3 反比例函数 ① ;② ;
③ ;④ 的图象:
(1)位于第一、三象限的是 ;
(2)位于第二、四象限的是 .
② ④
① ③
2﹑已知 k<0, 则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
x
k
y
x
y
0
x
x
y
0
x
y
0
(A)
(B)
(C)
(D)
D
三.导学施教
由两支曲线组成的.因此称它的图象为双曲线;
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
反比例函数的图象和性质
形状
位置
增减性
图象的发展趋势
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 的常数)
( k≠0的常数 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
二四象限
y随x的增大而减小
在每个象限内, y随x的增大而增大
比较正比例函数和反比例函数的区别
二四象限
在每个象限内,y随x的增大而减小
26.1.2反比例函数的
图象与性质
第一课时
一次函数
y = kx + b(k ≠ 0)
新课导入
一条直线
二次函数
y = ax2 + bx + c(a ≠ 0)
一条抛物线
函数图象画法
列
表
描
点
连
线
描点法
画出反比例函数 和 的图象.
反比例函数的图象和画法
知识点1
x … -12 -6 -4 -3 -2 -1 1 2 3 4 6 12 …
… -1.5 -2 6 2 1 …
… -1 -2 -4 -6 12 4 3 1 …
3
1.5
-6
-3
-1
-0.5
-12
6
-3
2
0.5
列表
5
10
x
5
10
-5
-10
-5
-10
y
O
描点连线
1.图像形状
2.图象位置
3.图象趋势
4.增减性
(1)函数图象分别位于第一、第三象限;
(2)在每一个象限内,y随 x 的增大而减小.
一般地,当 k >0 时,对于反比例函数 由函数图象(图26.1-2),并结合解析式,我们发现:
图26.1-2
x … -12 -6 -4 -3 -2 -1 1 2 3 4 6 12 …
… 1.5 2 -6 -2 -1 …
-3
-1.5
6
3
1
0.5
-0.5
列表
画出反比例函数 和 的图象.
画出反比例函数 的图象.
第二象限
第四象限
在每一个象限内,y随 x 的增大而增大.
难点突破
1.图像形状
2.图象位置
3.图象趋势
4.增减性
(1)函数图象分别位于第二、第四象限;
(2)在每一个象限内,y随 x 的增大而增大.
一般地,当 k <0 时,对于反比例函数 由函数图象,并结合解析式,我们发现:
归纳
(1)当 k > 0 时,函数图象分别位于第一、第三象限;在每一个象限内,y 随 x 的增大而减小.
(2)当 k < 0 时,函数图象分别位于第二、第四象限;在每一个象限内,y 随 x 的增大而增大.
一般地,反比例函数 (k≠0)的图象是双曲线,它具有以下性质:
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
一、三
二、四
减小
增大
1.下列图象中是反比例函数图象的是( )
C
A B C D
课堂演练
2.如图是下列四个函数中哪一个函数的图象( )
A. y = 5x
B. y = 2x + 3
C.
D.
C
练习3 反比例函数 ① ;② ;
③ ;④ 的图象:
(1)位于第一、三象限的是 ;
(2)位于第二、四象限的是 .
② ④
① ③
2﹑已知 k<0, 则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
x
k
y
x
y
0
x
x
y
0
x
y
0
(A)
(B)
(C)
(D)
D
三.导学施教
由两支曲线组成的.因此称它的图象为双曲线;
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
反比例函数的图象和性质
形状
位置
增减性
图象的发展趋势
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 的常数)
( k≠0的常数 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
二四象限
y随x的增大而减小
在每个象限内, y随x的增大而增大
比较正比例函数和反比例函数的区别
二四象限
在每个象限内,y随x的增大而减小
