华师大版数学七年级下册 第9章 多边形达标达标测试卷(二)(含答案)
文档属性
| 名称 | 华师大版数学七年级下册 第9章 多边形达标达标测试卷(二)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 17:20:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第9章 多边形 达标测试卷(二)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列图形中,不是运用三角形稳定性的是( )
A B C D
2.如图1,在△ABC中,BC边上的高为( )
A.BF B.CF C.BD D.AE
图1
3.下列长度的线段能组成三角形的是( )
A.1cm,2cm,3cm B.4cm,5cm,10cm
C.6cm,8cm,13cm D.5cm,5cm,10cm
4.七边形的内角和是( )
A.360° B.540° C.720° D.900°
用正三角形和正方形镶嵌一个平面,在同一个顶点处,正三角形和正方形的个数之比
( )
A.1:1 B.1:2 C.2:3 D.3:2
6.下列条件中能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C B.∠A=∠B=∠C
C.∠A﹣∠B=90° D.∠A=2∠B=3∠C
7.我们知道,四边形有2条对角线,五边形有5条对角线,那么十二边形对角线的总条数
是( )
A.9 B.54 C.60 D.108
8.将一副三角尺按图2所示的方式放置,则∠1的度数为( )
A.95° B.100° C.105° D.115°
图2
9.将一个三角形纸片剪开并分成两个三角形,这两个三角形不可能( )
A.都是直角三角形 B.都是钝角三角形
C.都是锐角三角形 D.是一个直角三角形和一个钝角三角形
10.把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照图3所示的
方式叠放在一起,延长LG交AF于点P,则∠APG=( )
A.141° B.144° C.147° D.150°
图3
二.填空题(本大题共6小题,每小题3分,共18分)
11.钝角三角形三边上的中线的交点在此三角形 .(填“内”“外”或“边上”)
12.在△ABC中,AB=4,BC=7,则AC的长x的取值范围是 .
13.如图4,△ABC中,∠B=∠DAC,则∠BAC和∠ADC的大小关系是 .
图4
14.如图5,五边形ABCDE的外角中,∠1=∠2=∠3=∠4=75°,则∠A的度数是 .
图5
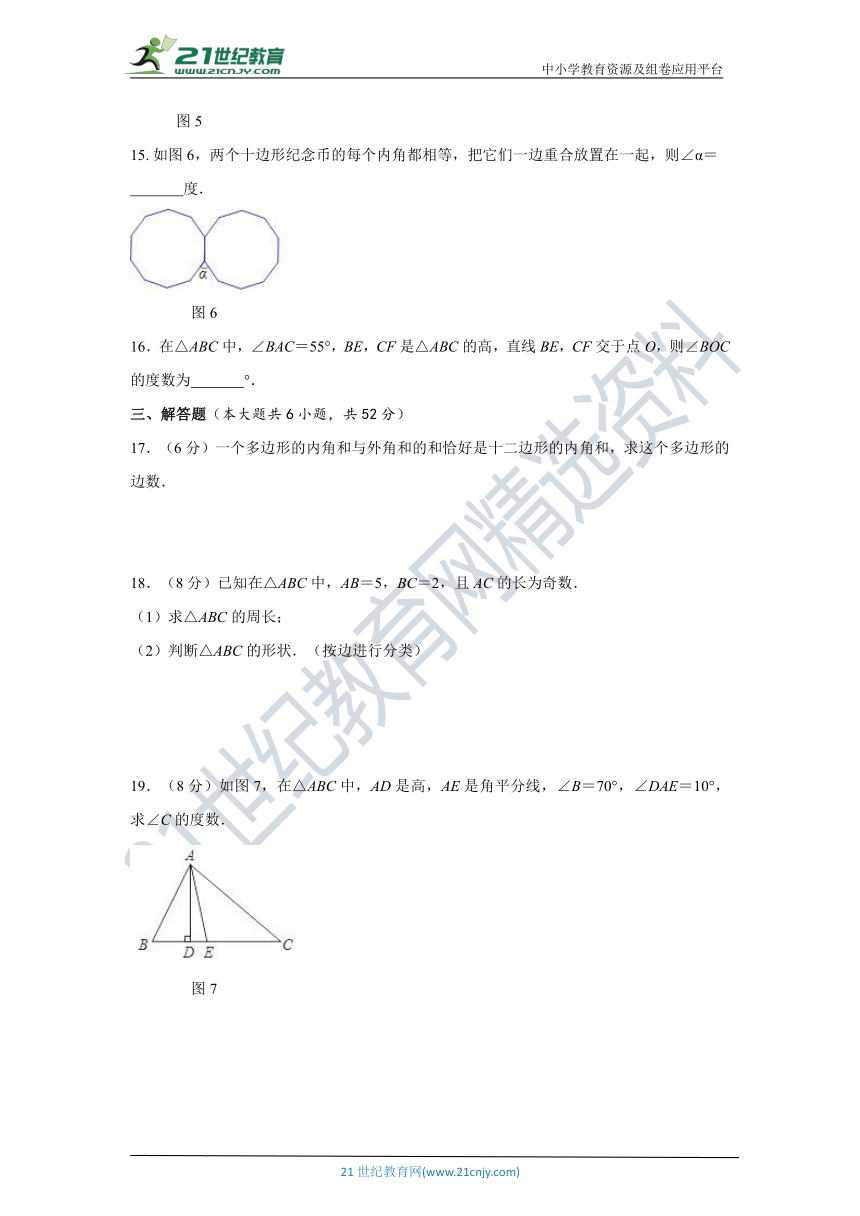
如图6,两个十边形纪念币的每个内角都相等,把它们一边重合放置在一起,则∠α=
度.
图6
16.在△ABC中,∠BAC=55°,BE,CF是△ABC的高,直线BE,CF交于点O,则∠BOC
的度数为 °.
三、解答题(本大题共6小题,共52分)
17.(6分)一个多边形的内角和与外角和的和恰好是十二边形的内角和,求这个多边形的
边数.
18.(8分)已知在△ABC中,AB=5,BC=2,且AC的长为奇数.
(1)求△ABC的周长;
(2)判断△ABC的形状.(按边进行分类)
19.(8分)如图7,在△ABC中,AD是高,AE是角平分线,∠B=70°,∠DAE=10°,求∠C的度数.
图7
20.(8分)已知△ABC中,三边长a,b,c满足a=b+2,b=c+1.
(1)试说明b一定大于3;
(2)若这个三角形的周长为22,求a,b,c的值.
21.(10分)如图8,已知六边形ABCDEF的每个内角都相等,连接AD.
(1)若∠1=48°,求∠2的度数;
(2)试说明AB∥DE.
图8
22.(12分)(1)如图9-①,在∠A内部有一点P,连接BP,CP,试说明∠P=∠1+∠A+∠2;
(2)如图9-②,利用上面的结论,在五角星中,∠A+∠B+∠C+∠D+∠E= ;
(3)如图9-③,如果在∠BAC间有两个向上突起的角,请你根据前面的结论猜想∠1,∠2,∠3,∠4,∠5,∠A之间有什么数量关系,直接写出结论即可.
图9
附加题(20分,不计入总分)
问题解决:如图1,△ABC中,AF为BC边上的中线,则S△ABF= S△ABC.
问题探究:(1)如图2,CD,BE分别是△ABC的中线,S△BOC与S四边形ADOE相等吗?
解:在△ABC中,由问题解决的结论,可得S△BCD=S△ABC,S△ABE=S△ABC.
所以S△BCD=S△ABE.
所以S△BCD﹣S△BOD=S△ABE﹣S△BOD,即S△BOC=S四边形ADOE.
(2)图2中,仿照(1)的方法,试说明S△BOD=S△COE.
(3)如图3,CD,BE,AF分别是△ABC的中线,则S△BOC= S△ABC,S△AOE=
S△ABC,S△BOD= S△ABF.
问题拓展:
(1)如图4,E,F分别为四边形ABCD的边AD,BC的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴影= S四边形ABCD.
(2)如图5,E,F,G,H分别为四边形ABCD的边AD,BC,AB,CD的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴影= S四边形ABCD.
第9章 多边形 达标测试卷(二)
一、1.C 2.D 3.C 4.D 5.D 6.A 7.B 8.C 9.C 10.B
二、11.内 12.3<x<11 13.相等
14.120° 15.72 16.55°或125°
三、17.解:设这个多边形的边数为n.
根据题意,得(n﹣2)×180°+360°=(12﹣2)×180°.
解得n=10.
所以这个多边形的边数为10.
18.解:(1)根据题意,得5﹣2<AC<5+2,即3<AC<7.
因为AC的长为奇数,所以AC=5.所以△ABC的周长为5+5+2=12.
(2)因为AB=AC=5,所以△ABC是等腰三角形.
19.解:因为AD是△ABC的高,∠B=70°,所以∠BAD=20°.
因为∠DAE=10°,所以∠BAE=∠BAD+∠DAE=20°+10°=30°.
因为AE是△ABC的角平分线,所以∠BAC=2∠BAE=60°.所以∠C=180°﹣∠B﹣
∠BAC=180°﹣70°﹣60°=50°.
20.解:(1)因为a=b+2,所以b=a﹣2.
因为b=c+1,所以a﹣2=c+1,即a﹣c=3.所以b一定大于3.
因为b=c+1,所以c=b﹣1.
因为a=b+2,a+b+c=22,所以b+2+b+b﹣1=22,解得b=7.所以a=b+2=9,c=b﹣1=6.
21.解:(1)因为六边形ABCDEF的各内角相等,所以每个内角的大小为(6-2)×180°÷6=120°.所以∠E=∠F=∠FAB=120°.
因为∠1=48°,所以∠FAD=∠FAB﹣∠1=120°﹣48°=72°.
因为四边形AFED的内角和为360°,所以∠2=360°﹣∠FAD﹣∠F﹣∠E=360°﹣72°﹣120°﹣120°=48°.
(2)因为∠1=∠FAB-∠FAD=120°﹣∠FAD,∠2=360°﹣∠F﹣∠E﹣∠FAD=360°﹣120°﹣120°﹣∠FAD=120°﹣∠DAF,所以∠1=∠2.所以AB∥DE.
22.解:(1)如图1,连接AP并延长.
因为∠3是△ABP的外角,∠4是△ACP的外角,所以∠3=∠2+∠BAP,∠4=∠1+∠PAC.所以∠3+∠4=∠2+∠BAP+∠1+∠PAC,即∠BPC=∠1+∠BAC+∠2.
(2)180°
∠4+∠5=∠1+∠2+∠3+∠BAC.提示:连接AD.由(1)中结论,可得∠4=∠3+
∠BAD+∠PDA,∠5=∠ADG+∠DAC+∠1,所以∠4+∠5=∠1+∠2+∠3+∠BAC.
附加题
解:问题解决:
问题探究:(2)在△ABC中,由问题解决的结论可得,S△BCD=S△ABC,S△BCE=S△ABC.
所以S△BCD=S△BCE.
所以S△BCD﹣S△BOC=S△BCE﹣S△BOC,即S△BOD=S△COE.
(3)
问题拓展:(1) 提示:连接BD.因为BE是△ABD的中线,所以S△ABE=S△BDE.
因为DF是△BCD的中线,所以S△BDF=S△DFC,所以S阴影=S四边形ABCD.
(2) 提示:连接BD,设BE交DG于M,BH交DF于N.由问题探究,可知S△BDM=S△ABD,S△BDN=S△BDC,所以S阴影=(S△ABD+S△BDC)=S四边形ABCD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第9章 多边形 达标测试卷(二)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列图形中,不是运用三角形稳定性的是( )
A B C D
2.如图1,在△ABC中,BC边上的高为( )
A.BF B.CF C.BD D.AE
图1
3.下列长度的线段能组成三角形的是( )
A.1cm,2cm,3cm B.4cm,5cm,10cm
C.6cm,8cm,13cm D.5cm,5cm,10cm
4.七边形的内角和是( )
A.360° B.540° C.720° D.900°
用正三角形和正方形镶嵌一个平面,在同一个顶点处,正三角形和正方形的个数之比
( )
A.1:1 B.1:2 C.2:3 D.3:2
6.下列条件中能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C B.∠A=∠B=∠C
C.∠A﹣∠B=90° D.∠A=2∠B=3∠C
7.我们知道,四边形有2条对角线,五边形有5条对角线,那么十二边形对角线的总条数
是( )
A.9 B.54 C.60 D.108
8.将一副三角尺按图2所示的方式放置,则∠1的度数为( )
A.95° B.100° C.105° D.115°
图2
9.将一个三角形纸片剪开并分成两个三角形,这两个三角形不可能( )
A.都是直角三角形 B.都是钝角三角形
C.都是锐角三角形 D.是一个直角三角形和一个钝角三角形
10.把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照图3所示的
方式叠放在一起,延长LG交AF于点P,则∠APG=( )
A.141° B.144° C.147° D.150°
图3
二.填空题(本大题共6小题,每小题3分,共18分)
11.钝角三角形三边上的中线的交点在此三角形 .(填“内”“外”或“边上”)
12.在△ABC中,AB=4,BC=7,则AC的长x的取值范围是 .
13.如图4,△ABC中,∠B=∠DAC,则∠BAC和∠ADC的大小关系是 .
图4
14.如图5,五边形ABCDE的外角中,∠1=∠2=∠3=∠4=75°,则∠A的度数是 .
图5
如图6,两个十边形纪念币的每个内角都相等,把它们一边重合放置在一起,则∠α=
度.
图6
16.在△ABC中,∠BAC=55°,BE,CF是△ABC的高,直线BE,CF交于点O,则∠BOC
的度数为 °.
三、解答题(本大题共6小题,共52分)
17.(6分)一个多边形的内角和与外角和的和恰好是十二边形的内角和,求这个多边形的
边数.
18.(8分)已知在△ABC中,AB=5,BC=2,且AC的长为奇数.
(1)求△ABC的周长;
(2)判断△ABC的形状.(按边进行分类)
19.(8分)如图7,在△ABC中,AD是高,AE是角平分线,∠B=70°,∠DAE=10°,求∠C的度数.
图7
20.(8分)已知△ABC中,三边长a,b,c满足a=b+2,b=c+1.
(1)试说明b一定大于3;
(2)若这个三角形的周长为22,求a,b,c的值.
21.(10分)如图8,已知六边形ABCDEF的每个内角都相等,连接AD.
(1)若∠1=48°,求∠2的度数;
(2)试说明AB∥DE.
图8
22.(12分)(1)如图9-①,在∠A内部有一点P,连接BP,CP,试说明∠P=∠1+∠A+∠2;
(2)如图9-②,利用上面的结论,在五角星中,∠A+∠B+∠C+∠D+∠E= ;
(3)如图9-③,如果在∠BAC间有两个向上突起的角,请你根据前面的结论猜想∠1,∠2,∠3,∠4,∠5,∠A之间有什么数量关系,直接写出结论即可.
图9
附加题(20分,不计入总分)
问题解决:如图1,△ABC中,AF为BC边上的中线,则S△ABF= S△ABC.
问题探究:(1)如图2,CD,BE分别是△ABC的中线,S△BOC与S四边形ADOE相等吗?
解:在△ABC中,由问题解决的结论,可得S△BCD=S△ABC,S△ABE=S△ABC.
所以S△BCD=S△ABE.
所以S△BCD﹣S△BOD=S△ABE﹣S△BOD,即S△BOC=S四边形ADOE.
(2)图2中,仿照(1)的方法,试说明S△BOD=S△COE.
(3)如图3,CD,BE,AF分别是△ABC的中线,则S△BOC= S△ABC,S△AOE=
S△ABC,S△BOD= S△ABF.
问题拓展:
(1)如图4,E,F分别为四边形ABCD的边AD,BC的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴影= S四边形ABCD.
(2)如图5,E,F,G,H分别为四边形ABCD的边AD,BC,AB,CD的中点,请直接写出阴影部分的面积与四边形ABCD的面积之间的数量关系:S阴影= S四边形ABCD.
第9章 多边形 达标测试卷(二)
一、1.C 2.D 3.C 4.D 5.D 6.A 7.B 8.C 9.C 10.B
二、11.内 12.3<x<11 13.相等
14.120° 15.72 16.55°或125°
三、17.解:设这个多边形的边数为n.
根据题意,得(n﹣2)×180°+360°=(12﹣2)×180°.
解得n=10.
所以这个多边形的边数为10.
18.解:(1)根据题意,得5﹣2<AC<5+2,即3<AC<7.
因为AC的长为奇数,所以AC=5.所以△ABC的周长为5+5+2=12.
(2)因为AB=AC=5,所以△ABC是等腰三角形.
19.解:因为AD是△ABC的高,∠B=70°,所以∠BAD=20°.
因为∠DAE=10°,所以∠BAE=∠BAD+∠DAE=20°+10°=30°.
因为AE是△ABC的角平分线,所以∠BAC=2∠BAE=60°.所以∠C=180°﹣∠B﹣
∠BAC=180°﹣70°﹣60°=50°.
20.解:(1)因为a=b+2,所以b=a﹣2.
因为b=c+1,所以a﹣2=c+1,即a﹣c=3.所以b一定大于3.
因为b=c+1,所以c=b﹣1.
因为a=b+2,a+b+c=22,所以b+2+b+b﹣1=22,解得b=7.所以a=b+2=9,c=b﹣1=6.
21.解:(1)因为六边形ABCDEF的各内角相等,所以每个内角的大小为(6-2)×180°÷6=120°.所以∠E=∠F=∠FAB=120°.
因为∠1=48°,所以∠FAD=∠FAB﹣∠1=120°﹣48°=72°.
因为四边形AFED的内角和为360°,所以∠2=360°﹣∠FAD﹣∠F﹣∠E=360°﹣72°﹣120°﹣120°=48°.
(2)因为∠1=∠FAB-∠FAD=120°﹣∠FAD,∠2=360°﹣∠F﹣∠E﹣∠FAD=360°﹣120°﹣120°﹣∠FAD=120°﹣∠DAF,所以∠1=∠2.所以AB∥DE.
22.解:(1)如图1,连接AP并延长.
因为∠3是△ABP的外角,∠4是△ACP的外角,所以∠3=∠2+∠BAP,∠4=∠1+∠PAC.所以∠3+∠4=∠2+∠BAP+∠1+∠PAC,即∠BPC=∠1+∠BAC+∠2.
(2)180°
∠4+∠5=∠1+∠2+∠3+∠BAC.提示:连接AD.由(1)中结论,可得∠4=∠3+
∠BAD+∠PDA,∠5=∠ADG+∠DAC+∠1,所以∠4+∠5=∠1+∠2+∠3+∠BAC.
附加题
解:问题解决:
问题探究:(2)在△ABC中,由问题解决的结论可得,S△BCD=S△ABC,S△BCE=S△ABC.
所以S△BCD=S△BCE.
所以S△BCD﹣S△BOC=S△BCE﹣S△BOC,即S△BOD=S△COE.
(3)
问题拓展:(1) 提示:连接BD.因为BE是△ABD的中线,所以S△ABE=S△BDE.
因为DF是△BCD的中线,所以S△BDF=S△DFC,所以S阴影=S四边形ABCD.
(2) 提示:连接BD,设BE交DG于M,BH交DF于N.由问题探究,可知S△BDM=S△ABD,S△BDN=S△BDC,所以S阴影=(S△ABD+S△BDC)=S四边形ABCD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
