华师大版数学七年级下册 第10章 轴对称、平移与旋转达达标测试卷(二)(含答案)
文档属性
| 名称 | 华师大版数学七年级下册 第10章 轴对称、平移与旋转达达标测试卷(二)(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第10章 轴对称、平移与旋转 达标测试卷(二)
一、选择题(本大题共10小题,每小题3分,共30分)
1. 下列图形中,△A′B′C′与△ABC成中心对称的是( )
A B C D
2.在6×6的网格中,将图1-①中的图形N平移后位置如图1-②所示,则下列图形N的平移方式正确的是( )
A.向下平移1格 B.向上平移1格
C.向上平移2格 D.向下平移2格
图1
3.如图2,△AOC≌△BOD,∠C与∠D是对应角,AC与BD是对应边.若AC=8 cm,AD=10 cm,OD=OC=2 cm,则OB的长为( )
A.8 cm B.10 cm C.2 cm D.4 cm
图2
4.如图3,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,下列说法不一定正确的是( )
A.AC=A′C′ B.AB∥B′C′ C.AA′⊥MN D.BO=B′O
图3
5.如图4,若△ABC与△DEF成中心对称,则对称中心是( )
A.点C B.点D C.线段BC的中点 D.线段FC的中点
图4
6.如图5,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为 ( )
A.60° B.75° C.85° D.90°
图5
7.(2019年河北)如图6,在小等边三角形组成的网格中,已有6个小等边三角形涂黑,还需涂黑n个小等边三角形,使它们与原来涂黑的小等边三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.10 B.6 C.3 D.2
图6
8.如图7,△ABC的面积为6,边AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,点P在直线AD上,则线段BP的长不可能是( )
A.3 B.4 C.5 D.6
图7
9.如图8,在△ABC中,∠BAC=30°,将△ABC绕点A逆时针旋转120°到△AB1C1,连接BB1.若AC1∥BB1,则∠ABB1的度数为( )
A.45° B.60° C.70° D.30°
图8
10.(2019年南京)如图9,△A'B'C'是由△ABC经过平移得到的,△A'B'C'还可以看作是
△ABC经过怎样的图形变化得到?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
A.①④ B.②③ C.②④ D.③④
图9
二、填空题(本大题共6小题,每小题3分,共18分)
11.下列说法:①只有两个三角形才可能完全重合;②若两个图形全等,则它们的形状和大小一定都相同;③两个正方形一定是全等图形;④边数相同的图形一定能互相重合.其中错误的说法是______.(填序号)
12.如图10,直线l是四边形ABCD的对称轴,AD∥BC,∠D=128°,则∠B的度数为 °.
图10
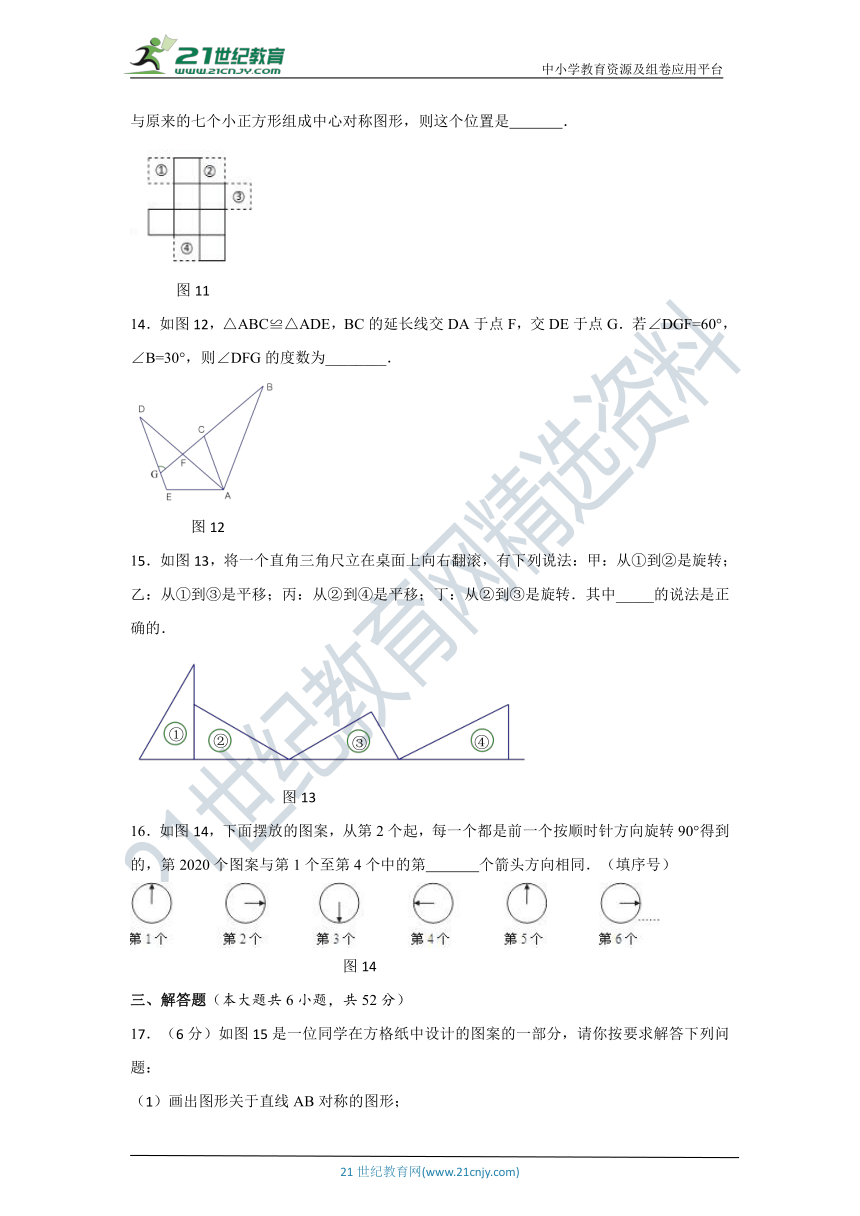
13.图11中所有的小正方形都全等,若再添加一个小正方形在①②③④的某一位置,使它与原来的七个小正方形组成中心对称图形,则这个位置是 .
图11
14.如图12,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G.若∠DGF=60°,∠B=30°,则∠DFG的度数为________.
图12
15.如图13,将一个直角三角尺立在桌面上向右翻滚,有下列说法:甲:从①到②是旋转;乙:从①到③是平移;丙:从②到④是平移;丁:从②到③是旋转.其中_____的说法是正确的.
图13
16.如图14,下面摆放的图案,从第2个起,每一个都是前一个按顺时针方向旋转90°得到的,第2020个图案与第1个至第4个中的第 个箭头方向相同.(填序号)
图14
三、解答题(本大题共6小题,共52分)
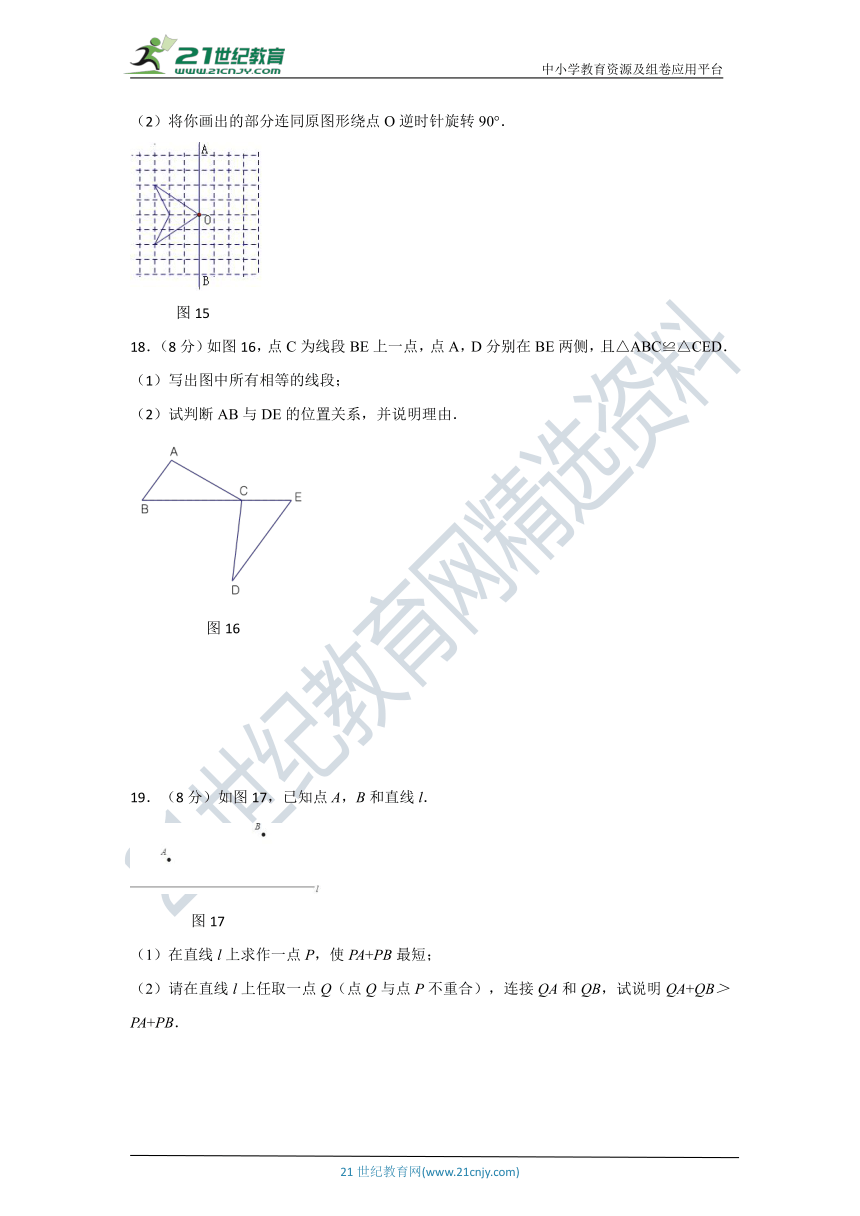
17.(6分)如图15是一位同学在方格纸中设计的图案的一部分,请你按要求解答下列问题:
(1)画出图形关于直线AB对称的图形;
(2)将你画出的部分连同原图形绕点O逆时针旋转90°.
图15
18.(8分)如图16,点C为线段BE上一点,点A,D分别在BE两侧,且△ABC≌△CED.
(1)写出图中所有相等的线段;
(2)试判断AB与DE的位置关系,并说明理由.
图16
19.(8分)如图17,已知点A,B和直线l.
图17
(1)在直线l上求作一点P,使PA+PB最短;
(2)请在直线l上任取一点Q(点Q与点P不重合),连接QA和QB,试说明QA+QB>PA+PB.
20.(8分)有如下问题:“如图18,将直角三角形ABC(∠ABC=90°)沿CB方向平移4 cm得到直角三角形DEF.已知AG=2 cm,DE=6 cm,求阴影部分的面积.”针对这一问题,小亮和小颖有如下谈话:
小颖为什么说阴影部分的面积等于梯形GBED的面积?请你按小颖的思路求出阴影部分的面积.
21.(10分)如图19,网格中每个小正方形的边长为1,请你认真观察图中的三个网格中阴影部分构成的图案,解答下列问题:
图19
(1)这三个图案都具有以下共同特征:
①都是________对称图形,都不是________对称图形;②面积都是________个平方单位.
(2)请在图19的空白网格中设计出具备上述特征的图案,要求所画图案不能与所给出的图案相同,且不能由所给的图案通过平移或旋转得到.
22.(12分)如图20,点O在直线AB上,OC⊥AB,在△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE的一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE= ;
(2)试探索:在△ODE旋转的过程中,∠AOD与∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转的过程中,若∠AOE=7∠COD,试求∠AOE的度数.
图20
附加题(20分,不计入总分)
阅读材料:课堂上,老师设计了一个活动:将一个4×4的正方形网格沿着网格线划分成两
部分(分别用阴影和空白表示),使得这两部分图形是全等的,请同学们尝试给出划分的方
法.约定:如果两位同学的划分结果经过旋转、翻折后能够重合,那么就认为他们的划分方
法相同.
小方、小易和小红分别对网格进行了划分,结果如图①,图②,图③所示.
小方说:“我们三个人的划分方法都是正确的.但是将小红的整个图形(图③)逆时针旋转90°后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同.”
老师说:“小方说得对.”
完成下列问题:
(1)图④的划分方法是否正确?
(2)判断图⑤的划分方法与图②小易的划分方法是否相同,并说明理由.
(3)请你再想出一种与已有方法不同的划分方法,使之满足上述条件,并在图⑥中画出来.
第10章 轴对称、平移与旋转 达标测试卷(二)
一、1.A 2.D 3.A 4.B 5.D 6.C 7.C 8.A 9.D 10.D
二、11.①③④ 12.52 13.③ 14.90° 15.甲与丁 16.4
三、17.略.
18.解:(1)AB=CE,AC=CD,BC=ED.
(2)AB∥DE,理由如下:
因为△ABC≌△CED,所以∠B=∠E.所以AB∥DE.
19.解:(1)如图1,作点A关于直线l的对称点A′,连接A′B交直线l于点P,则点P即为所求.
图1
(2)在直线l上任取不同于点P的一点Q,连接PA,QA,QB.
因为点A与点A′关于直线l对称,点P,Q在直线l上,所以PA=PA′,QA=QA′.
因为QA′+QB>A′B,所以QA+QB>A′B,即QA+QB>A′P+BP.所以QA+QB>PA+PB.
20.解:因为平移前后两个图形的形状和大小都相同,所以S△ABC=S△DEF.所以S△ABC-S△BFG=
S△DEF-S△BFG,即S阴影=S梯形GBED.
因为AB=DE=6 cm,AG=2 cm,所以BG=AB-AG=6-2=4(cm).
因为BE=4cm,所以S梯形GBED=(cm2).
21.(1)①中心 轴 ②4
(2)略.
22.解:(1)130°
(2)在△ODE旋转的过程中,∠AOD与∠COE的差不发生变化,理由如下:
分两种情况:
①如图2,当OD在OA与OC之间时,因为∠AOD+∠COD=90°,∠COD+∠COE=60°,所以∠AOD﹣∠COE=(∠AOD+∠COD)-(∠COD+∠COE)=90°﹣60°=30°.
②如图3,当OD在OC与OB之间时,因为∠AOD=∠AOC+∠COD=90°+∠COD,∠COE=∠DOE+∠COD=60°+∠COD,所以∠AOD﹣∠COE=(90°+∠COD)﹣(60°+∠COD)=30°.
综上,在△ODE旋转的过程中,∠AOD与∠COE的差不发生变化,为30°.
(3)分两种情况:
如图2,当OD在OA与OC之间时,因为∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,所以90°+60°﹣∠COD=7∠COD,可得∠COD=18.75°,所以∠AOE=7×18.75°=131.25°.
如图3,当OD在OC与OB之间时,因为∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,所以90°+60°+∠COD=7∠COD,可得∠COD=25°,所以∠AOE=7×25°=175°.
综上,∠AOE的度数为131.25°或175°.
附加题
解:(1)题图④中,阴影部分与空白部分面积不相同,所以阴影部分与空白部分不全等,
所以题图④的划分方法不正确,
(2)题图⑤的划分方法与题图②小易的划分方法相同,理由:题图⑤经过旋转、翻折后能够与题图②重合.
(3)如图所示:
①
②
①
②
③
④
可以把它转化成梯形GBED的面积来求啊!
阴影部分是一个梯形,不知道它的两底和高,怎样求它的面积呢?
小亮
小颖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第10章 轴对称、平移与旋转 达标测试卷(二)
一、选择题(本大题共10小题,每小题3分,共30分)
1. 下列图形中,△A′B′C′与△ABC成中心对称的是( )
A B C D
2.在6×6的网格中,将图1-①中的图形N平移后位置如图1-②所示,则下列图形N的平移方式正确的是( )
A.向下平移1格 B.向上平移1格
C.向上平移2格 D.向下平移2格
图1
3.如图2,△AOC≌△BOD,∠C与∠D是对应角,AC与BD是对应边.若AC=8 cm,AD=10 cm,OD=OC=2 cm,则OB的长为( )
A.8 cm B.10 cm C.2 cm D.4 cm
图2
4.如图3,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,下列说法不一定正确的是( )
A.AC=A′C′ B.AB∥B′C′ C.AA′⊥MN D.BO=B′O
图3
5.如图4,若△ABC与△DEF成中心对称,则对称中心是( )
A.点C B.点D C.线段BC的中点 D.线段FC的中点
图4
6.如图5,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为 ( )
A.60° B.75° C.85° D.90°
图5
7.(2019年河北)如图6,在小等边三角形组成的网格中,已有6个小等边三角形涂黑,还需涂黑n个小等边三角形,使它们与原来涂黑的小等边三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.10 B.6 C.3 D.2
图6
8.如图7,△ABC的面积为6,边AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,点P在直线AD上,则线段BP的长不可能是( )
A.3 B.4 C.5 D.6
图7
9.如图8,在△ABC中,∠BAC=30°,将△ABC绕点A逆时针旋转120°到△AB1C1,连接BB1.若AC1∥BB1,则∠ABB1的度数为( )
A.45° B.60° C.70° D.30°
图8
10.(2019年南京)如图9,△A'B'C'是由△ABC经过平移得到的,△A'B'C'还可以看作是
△ABC经过怎样的图形变化得到?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
A.①④ B.②③ C.②④ D.③④
图9
二、填空题(本大题共6小题,每小题3分,共18分)
11.下列说法:①只有两个三角形才可能完全重合;②若两个图形全等,则它们的形状和大小一定都相同;③两个正方形一定是全等图形;④边数相同的图形一定能互相重合.其中错误的说法是______.(填序号)
12.如图10,直线l是四边形ABCD的对称轴,AD∥BC,∠D=128°,则∠B的度数为 °.
图10
13.图11中所有的小正方形都全等,若再添加一个小正方形在①②③④的某一位置,使它与原来的七个小正方形组成中心对称图形,则这个位置是 .
图11
14.如图12,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G.若∠DGF=60°,∠B=30°,则∠DFG的度数为________.
图12
15.如图13,将一个直角三角尺立在桌面上向右翻滚,有下列说法:甲:从①到②是旋转;乙:从①到③是平移;丙:从②到④是平移;丁:从②到③是旋转.其中_____的说法是正确的.
图13
16.如图14,下面摆放的图案,从第2个起,每一个都是前一个按顺时针方向旋转90°得到的,第2020个图案与第1个至第4个中的第 个箭头方向相同.(填序号)
图14
三、解答题(本大题共6小题,共52分)
17.(6分)如图15是一位同学在方格纸中设计的图案的一部分,请你按要求解答下列问题:
(1)画出图形关于直线AB对称的图形;
(2)将你画出的部分连同原图形绕点O逆时针旋转90°.
图15
18.(8分)如图16,点C为线段BE上一点,点A,D分别在BE两侧,且△ABC≌△CED.
(1)写出图中所有相等的线段;
(2)试判断AB与DE的位置关系,并说明理由.
图16
19.(8分)如图17,已知点A,B和直线l.
图17
(1)在直线l上求作一点P,使PA+PB最短;
(2)请在直线l上任取一点Q(点Q与点P不重合),连接QA和QB,试说明QA+QB>PA+PB.
20.(8分)有如下问题:“如图18,将直角三角形ABC(∠ABC=90°)沿CB方向平移4 cm得到直角三角形DEF.已知AG=2 cm,DE=6 cm,求阴影部分的面积.”针对这一问题,小亮和小颖有如下谈话:
小颖为什么说阴影部分的面积等于梯形GBED的面积?请你按小颖的思路求出阴影部分的面积.
21.(10分)如图19,网格中每个小正方形的边长为1,请你认真观察图中的三个网格中阴影部分构成的图案,解答下列问题:
图19
(1)这三个图案都具有以下共同特征:
①都是________对称图形,都不是________对称图形;②面积都是________个平方单位.
(2)请在图19的空白网格中设计出具备上述特征的图案,要求所画图案不能与所给出的图案相同,且不能由所给的图案通过平移或旋转得到.
22.(12分)如图20,点O在直线AB上,OC⊥AB,在△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE的一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE= ;
(2)试探索:在△ODE旋转的过程中,∠AOD与∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转的过程中,若∠AOE=7∠COD,试求∠AOE的度数.
图20
附加题(20分,不计入总分)
阅读材料:课堂上,老师设计了一个活动:将一个4×4的正方形网格沿着网格线划分成两
部分(分别用阴影和空白表示),使得这两部分图形是全等的,请同学们尝试给出划分的方
法.约定:如果两位同学的划分结果经过旋转、翻折后能够重合,那么就认为他们的划分方
法相同.
小方、小易和小红分别对网格进行了划分,结果如图①,图②,图③所示.
小方说:“我们三个人的划分方法都是正确的.但是将小红的整个图形(图③)逆时针旋转90°后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同.”
老师说:“小方说得对.”
完成下列问题:
(1)图④的划分方法是否正确?
(2)判断图⑤的划分方法与图②小易的划分方法是否相同,并说明理由.
(3)请你再想出一种与已有方法不同的划分方法,使之满足上述条件,并在图⑥中画出来.
第10章 轴对称、平移与旋转 达标测试卷(二)
一、1.A 2.D 3.A 4.B 5.D 6.C 7.C 8.A 9.D 10.D
二、11.①③④ 12.52 13.③ 14.90° 15.甲与丁 16.4
三、17.略.
18.解:(1)AB=CE,AC=CD,BC=ED.
(2)AB∥DE,理由如下:
因为△ABC≌△CED,所以∠B=∠E.所以AB∥DE.
19.解:(1)如图1,作点A关于直线l的对称点A′,连接A′B交直线l于点P,则点P即为所求.
图1
(2)在直线l上任取不同于点P的一点Q,连接PA,QA,QB.
因为点A与点A′关于直线l对称,点P,Q在直线l上,所以PA=PA′,QA=QA′.
因为QA′+QB>A′B,所以QA+QB>A′B,即QA+QB>A′P+BP.所以QA+QB>PA+PB.
20.解:因为平移前后两个图形的形状和大小都相同,所以S△ABC=S△DEF.所以S△ABC-S△BFG=
S△DEF-S△BFG,即S阴影=S梯形GBED.
因为AB=DE=6 cm,AG=2 cm,所以BG=AB-AG=6-2=4(cm).
因为BE=4cm,所以S梯形GBED=(cm2).
21.(1)①中心 轴 ②4
(2)略.
22.解:(1)130°
(2)在△ODE旋转的过程中,∠AOD与∠COE的差不发生变化,理由如下:
分两种情况:
①如图2,当OD在OA与OC之间时,因为∠AOD+∠COD=90°,∠COD+∠COE=60°,所以∠AOD﹣∠COE=(∠AOD+∠COD)-(∠COD+∠COE)=90°﹣60°=30°.
②如图3,当OD在OC与OB之间时,因为∠AOD=∠AOC+∠COD=90°+∠COD,∠COE=∠DOE+∠COD=60°+∠COD,所以∠AOD﹣∠COE=(90°+∠COD)﹣(60°+∠COD)=30°.
综上,在△ODE旋转的过程中,∠AOD与∠COE的差不发生变化,为30°.
(3)分两种情况:
如图2,当OD在OA与OC之间时,因为∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,所以90°+60°﹣∠COD=7∠COD,可得∠COD=18.75°,所以∠AOE=7×18.75°=131.25°.
如图3,当OD在OC与OB之间时,因为∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,所以90°+60°+∠COD=7∠COD,可得∠COD=25°,所以∠AOE=7×25°=175°.
综上,∠AOE的度数为131.25°或175°.
附加题
解:(1)题图④中,阴影部分与空白部分面积不相同,所以阴影部分与空白部分不全等,
所以题图④的划分方法不正确,
(2)题图⑤的划分方法与题图②小易的划分方法相同,理由:题图⑤经过旋转、翻折后能够与题图②重合.
(3)如图所示:
①
②
①
②
③
④
可以把它转化成梯形GBED的面积来求啊!
阴影部分是一个梯形,不知道它的两底和高,怎样求它的面积呢?
小亮
小颖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
