2021-2022学年九年级数学人教版下册26.1.2反比例函数的几何性质 课件(共47张PPT)
文档属性
| 名称 | 2021-2022学年九年级数学人教版下册26.1.2反比例函数的几何性质 课件(共47张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 00:00:00 | ||
图片预览






文档简介
(共47张PPT)
第二十六章
反比例函数的几何性质
人教版数学九年级下册
1.理解反比例函数的概念及几种等价形式.
2.能够快速绘出给定反比例函数的图像.
3.掌握反比例函数的性质,并应用解决数学问题.
学习目标
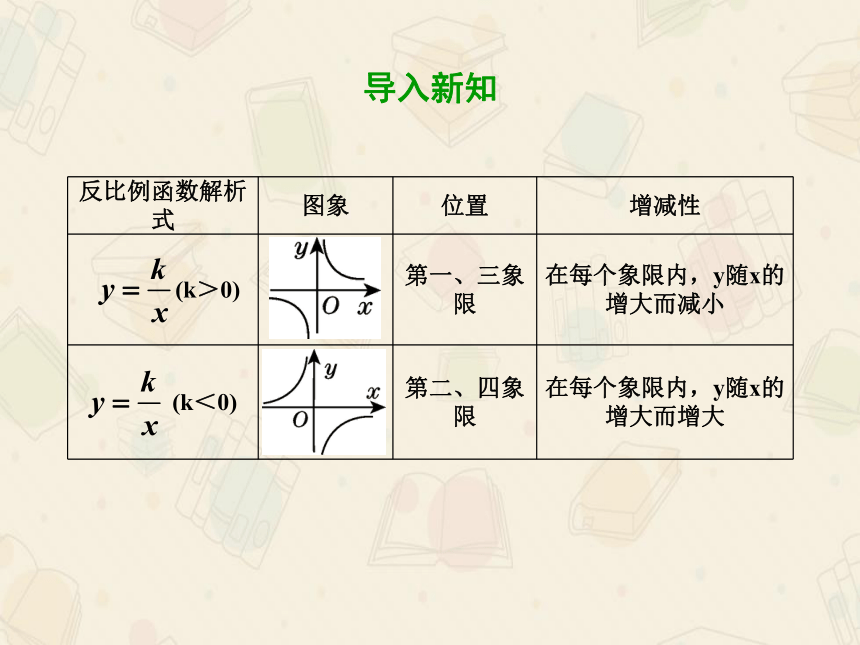
反比例函数解析式 图象 位置 增减性
(k>0) 第一、三象限 在每个象限内,y随x的增大而减小
(k<0) 第二、四象限 在每个象限内,y随x的增大而增大
导入新知
例1【中考·株洲】 已知反比例函数 的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
A.(-6,1) B.(1,6)
C.(2,-3) D.(3,-2)
1
知识点
反比例函数中k的几何性质
B
合作探究
导引:根据图象上点的坐标与解析式之间的关系,先求解析式,再确定点的坐标。将(2,3)带入解析式,的k=6.分别将A,B,C,D中点的坐标带入解析式,发现B中的点再图象上.
2
知识点
反比例函数中k的几何性质
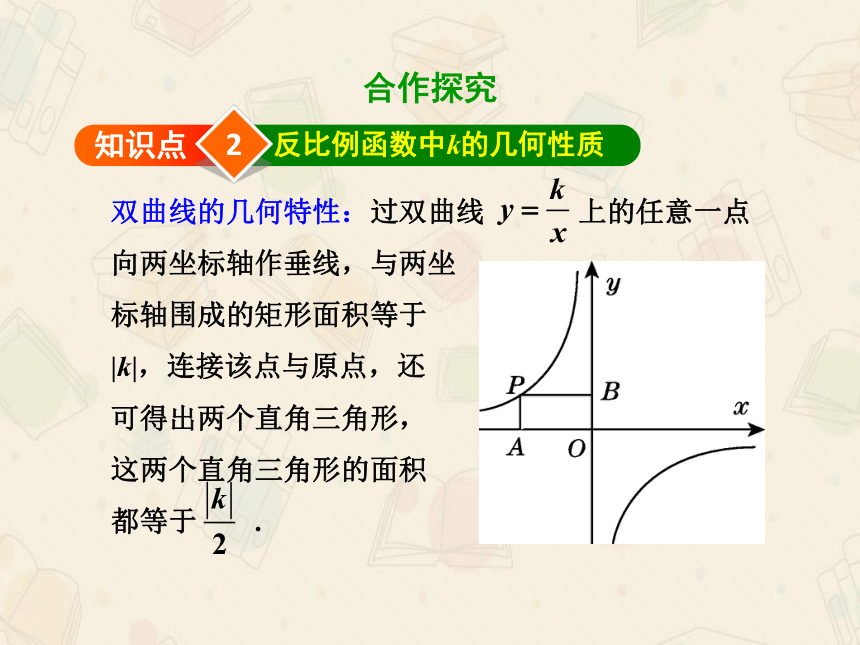
双曲线的几何特性:过双曲线 上的任意一点
向两坐标轴作垂线,与两坐
标轴围成的矩形面积等于
|k|,连接该点与原点,还
可得出两个直角三角形,
这两个直角三角形的面积
都等于 .
合作探究
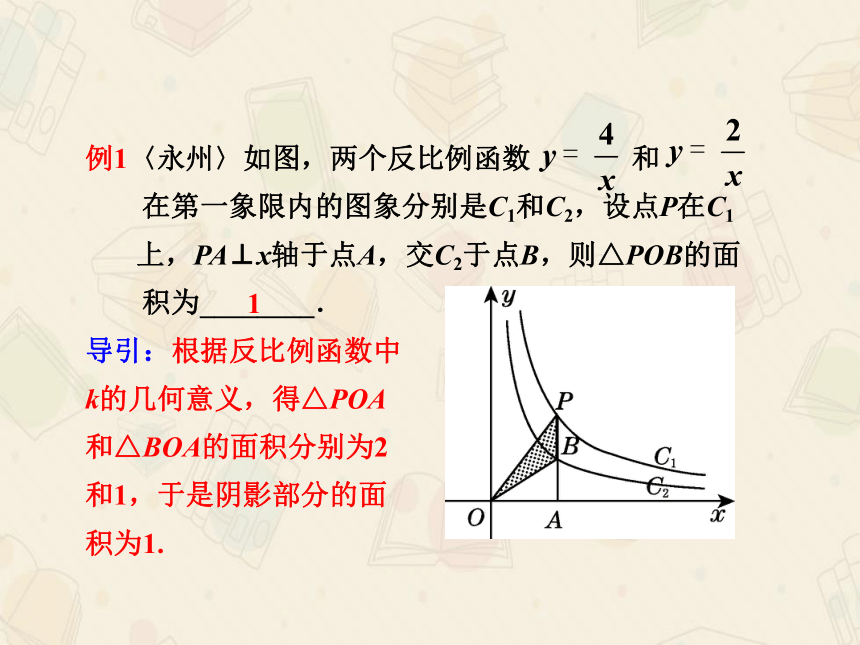
例1〈永州〉如图,两个反比例函数 和
在第一象限内的图象分别是C1和C2,设点P在C1
上,PA⊥x轴于点A,交C2于点B,则△POB的面
积为________.
导引:根据反比例函数中
k的几何意义,得△POA
和△BOA的面积分别为2
和1,于是阴影部分的面
积为1.
1
求阴影部分面积的方法:
当它无法直接求出时,一般都采用“转化”的
方法,将它转化为易求图形面积的和或差来进行计
算.如本例就是将阴影部分面积转化为两个与比例
系数相关的特殊三角形的面积的差来求,要注意转
化思想的运用.
新知小结
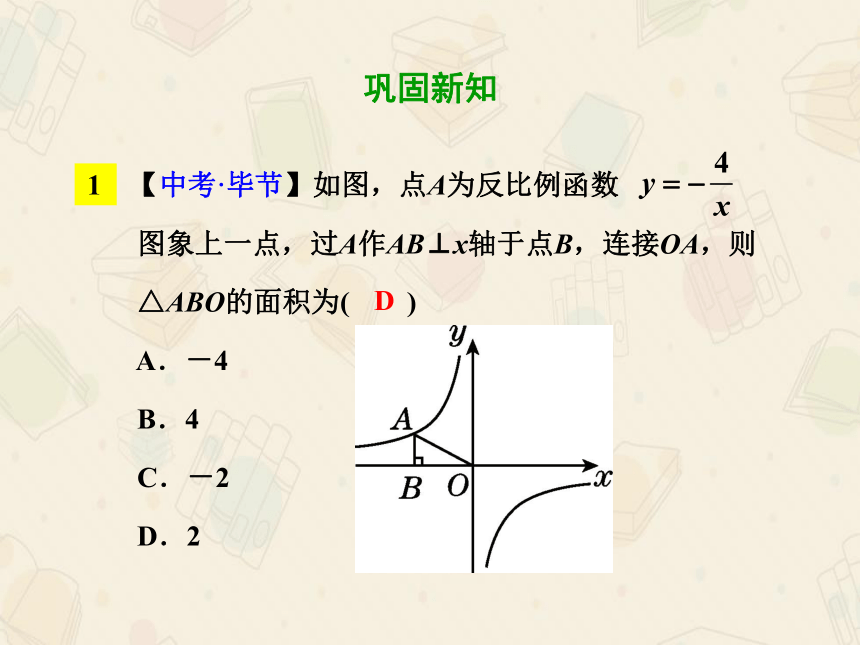
【中考·毕节】如图,点A为反比例函数
图象上一点,过A作AB⊥x轴于点B,连接OA,则
△ABO的面积为( )
A.-4
B.4
C.-2
D.2
D
巩固新知
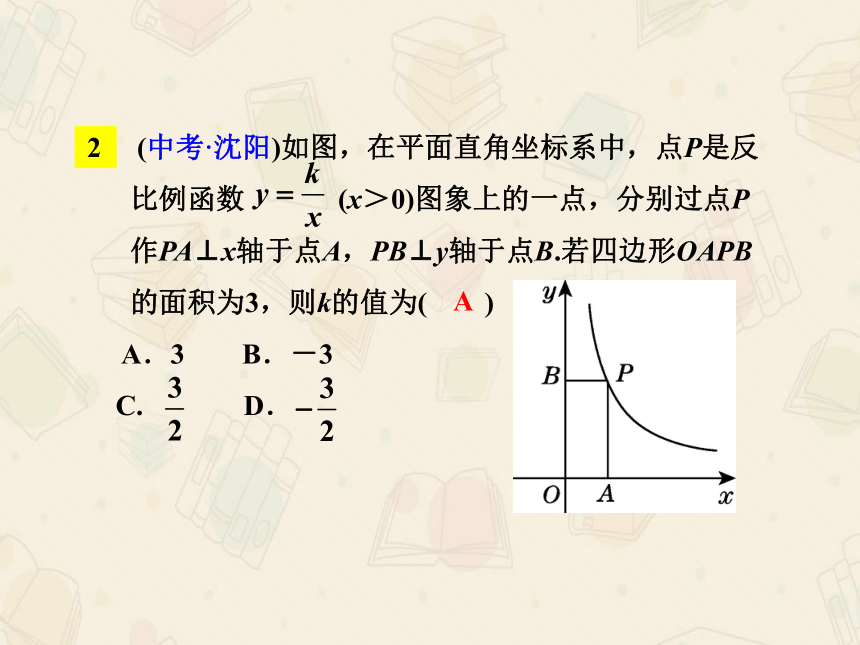
2 (中考·沈阳)如图,在平面直角坐标系中,点P是反
比例函数 (x>0)图象上的一点,分别过点P
作PA⊥x轴于点A,PB⊥y轴于点B.若四边形OAPB
的面积为3,则k的值为( )
A.3 B.-3
C. D.
A
【中考·青岛】一次函数y=kx+b(k≠0)的图象经
过A(-1,-4),B(2,2)两点,P为反比例函数
图象上一动点,O为坐标原点,过点P
作y轴的垂线,垂足为C,则△PCO的面积为
( )
A.2 B.4
C.8 D.不确定
A
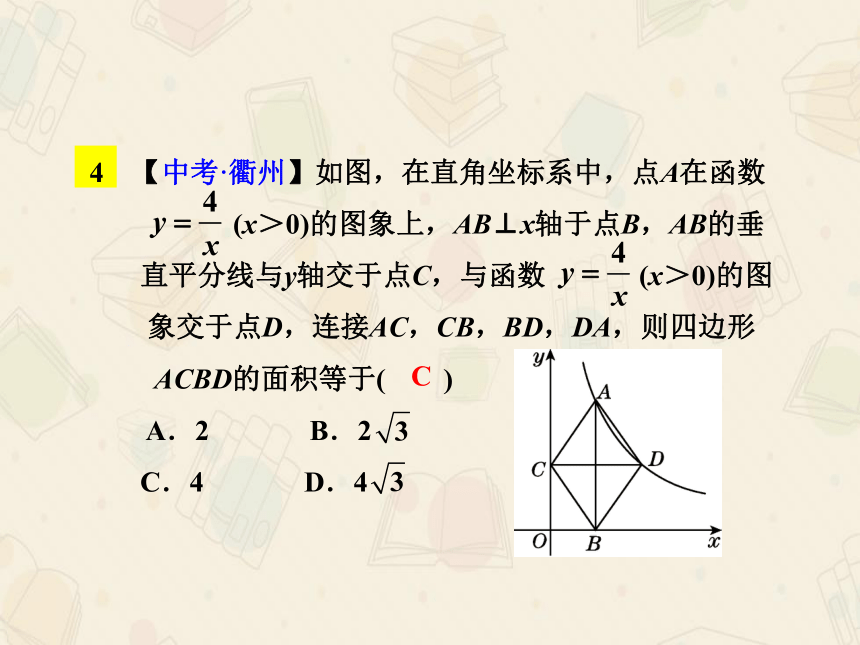
【中考·衢州】如图,在直角坐标系中,点A在函数
(x>0)的图象上,AB⊥x轴于点B,AB的垂
直平分线与y轴交于点C,与函数 (x>0)的图
象交于点D,连接AC,CB,BD,DA,则四边形
ACBD的面积等于( )
A.2 B.2
C.4 D.4
C
【中考·临沂】如图,在平面直角坐标系中,反比例
函数 (x>0)的图象与边长是6的正方形OABC
的两边AB,BC分别相交于M,N两点,△OMN的
面积为10.若动点P在x轴上,则PM+PN的最小值
是( )
A.6 B.10
C.2 D.2
C
3
知识点
反比例函数图象的对称性
反比例函数的图象关于原点成中心对称,也就
是把它的图象旋转180°与原图形重合,这是反比例
函数的一个重要性质,就常用来求点的坐标和图形
的面积等
合作探究
例2〈白银〉如图,在直角坐标系xOy中,直线y=mx与
双曲线 相交于A(-1,a),B两点,BC⊥x
轴,垂足为C,△AOC的面积是1.
(1)求m,n的值;
(2)求直线AC对应的函数解析式.
导引:(1)由题意,根据对称性得到点B的横坐标为1,确定
出点C的坐标,根据△AOC的面积求出点A的纵坐标,
确定出点A的坐标,将点A的坐标代入正比例函数与
反比例函数解析式,即可求出m与n的值;
(2)设直线AC对应的函数解析式为y=kx+b,将A,C
两点坐标分别代入求出k与b的值,即可确定出直线
AC对应的函数解析式.
解:(1)∵直线y=mx与双曲线 相交于A(-1,a),
B两点,
∴B点横坐标为1.
∴C(1,0).
∵△AOC的面积为1,
∴ ×a×1=1,∴a=2,
∴A(-1,2).
将A(-1,2)的坐标代入y=mx,
可得m=-2,n=-2.
(2)设直线AC对应的函数解析式为y=kx+b,
∵直线y=kx+b经过点A(-1,2),C(1,0),
∴ 解得
∴直线AC对应的函数解析式为y=-x+1.
反比例函数与正比例函数的图象都是中心对称
图形,所以在同一坐标系中,两个函数图象的两个交
点关于原点对称.
新知小结
【中考·天水】下列给出的函数中,其图象是中心对
称图形的是( )
①函数y=x;②函数y=x2;③函数
A.①② B.②③
C.①③ D.都不是
C
巩固新知
2 对于函数 ,下列说法错误的是 ( )
A.这个函数的图象位于第一、第三象限
B.这个函数的图象既是轴对称图形又是中心对称
图形
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
C
已知P为函数 的图象上一点,且点P到原点
的距离为2,则符合条件的点P有( )
A.0个 B.2个
C.4个 D.无数个
B
如图,边长为4的正方形ABCD的对称中心是坐
标原点O,AB∥x轴,BC∥y轴,反比例函数
与 的图象均与正方形ABCD的
边相交,则图中阴影部
分的面积之和是______.
8
1.反比例函数中k的几何性质:过双曲线 (k≠0)
上任一点向两坐标轴作垂线所得的矩形面积等于|k|;
向一坐标轴作垂线且与原点连线所得的三角形面积等
于 |k|.
2.双曲线关于直线y=x和直线y=-x成轴对称.
1
知识小结
归纳新知
如图,面积为5的矩形OABC的一个顶点B在反比例函数y=
的图象上,另三点在坐标轴上,则k=______.
易错点:已知图形面积求反比例函数比例系数k的值时,易忽视图象的位置.
-5
2
易错小结
|k|
课后练习
C
【答案】C
【答案】B
【答案】B
中心
坐标原点
(-a,-b)
轴
x
-x
(a,b)
(-b,-a)
【答案】D
C
【答案】C
第二十六章
反比例函数的几何性质
人教版数学九年级下册
1.理解反比例函数的概念及几种等价形式.
2.能够快速绘出给定反比例函数的图像.
3.掌握反比例函数的性质,并应用解决数学问题.
学习目标
反比例函数解析式 图象 位置 增减性
(k>0) 第一、三象限 在每个象限内,y随x的增大而减小
(k<0) 第二、四象限 在每个象限内,y随x的增大而增大
导入新知
例1【中考·株洲】 已知反比例函数 的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
A.(-6,1) B.(1,6)
C.(2,-3) D.(3,-2)
1
知识点
反比例函数中k的几何性质
B
合作探究
导引:根据图象上点的坐标与解析式之间的关系,先求解析式,再确定点的坐标。将(2,3)带入解析式,的k=6.分别将A,B,C,D中点的坐标带入解析式,发现B中的点再图象上.
2
知识点
反比例函数中k的几何性质
双曲线的几何特性:过双曲线 上的任意一点
向两坐标轴作垂线,与两坐
标轴围成的矩形面积等于
|k|,连接该点与原点,还
可得出两个直角三角形,
这两个直角三角形的面积
都等于 .
合作探究
例1〈永州〉如图,两个反比例函数 和
在第一象限内的图象分别是C1和C2,设点P在C1
上,PA⊥x轴于点A,交C2于点B,则△POB的面
积为________.
导引:根据反比例函数中
k的几何意义,得△POA
和△BOA的面积分别为2
和1,于是阴影部分的面
积为1.
1
求阴影部分面积的方法:
当它无法直接求出时,一般都采用“转化”的
方法,将它转化为易求图形面积的和或差来进行计
算.如本例就是将阴影部分面积转化为两个与比例
系数相关的特殊三角形的面积的差来求,要注意转
化思想的运用.
新知小结
【中考·毕节】如图,点A为反比例函数
图象上一点,过A作AB⊥x轴于点B,连接OA,则
△ABO的面积为( )
A.-4
B.4
C.-2
D.2
D
巩固新知
2 (中考·沈阳)如图,在平面直角坐标系中,点P是反
比例函数 (x>0)图象上的一点,分别过点P
作PA⊥x轴于点A,PB⊥y轴于点B.若四边形OAPB
的面积为3,则k的值为( )
A.3 B.-3
C. D.
A
【中考·青岛】一次函数y=kx+b(k≠0)的图象经
过A(-1,-4),B(2,2)两点,P为反比例函数
图象上一动点,O为坐标原点,过点P
作y轴的垂线,垂足为C,则△PCO的面积为
( )
A.2 B.4
C.8 D.不确定
A
【中考·衢州】如图,在直角坐标系中,点A在函数
(x>0)的图象上,AB⊥x轴于点B,AB的垂
直平分线与y轴交于点C,与函数 (x>0)的图
象交于点D,连接AC,CB,BD,DA,则四边形
ACBD的面积等于( )
A.2 B.2
C.4 D.4
C
【中考·临沂】如图,在平面直角坐标系中,反比例
函数 (x>0)的图象与边长是6的正方形OABC
的两边AB,BC分别相交于M,N两点,△OMN的
面积为10.若动点P在x轴上,则PM+PN的最小值
是( )
A.6 B.10
C.2 D.2
C
3
知识点
反比例函数图象的对称性
反比例函数的图象关于原点成中心对称,也就
是把它的图象旋转180°与原图形重合,这是反比例
函数的一个重要性质,就常用来求点的坐标和图形
的面积等
合作探究
例2〈白银〉如图,在直角坐标系xOy中,直线y=mx与
双曲线 相交于A(-1,a),B两点,BC⊥x
轴,垂足为C,△AOC的面积是1.
(1)求m,n的值;
(2)求直线AC对应的函数解析式.
导引:(1)由题意,根据对称性得到点B的横坐标为1,确定
出点C的坐标,根据△AOC的面积求出点A的纵坐标,
确定出点A的坐标,将点A的坐标代入正比例函数与
反比例函数解析式,即可求出m与n的值;
(2)设直线AC对应的函数解析式为y=kx+b,将A,C
两点坐标分别代入求出k与b的值,即可确定出直线
AC对应的函数解析式.
解:(1)∵直线y=mx与双曲线 相交于A(-1,a),
B两点,
∴B点横坐标为1.
∴C(1,0).
∵△AOC的面积为1,
∴ ×a×1=1,∴a=2,
∴A(-1,2).
将A(-1,2)的坐标代入y=mx,
可得m=-2,n=-2.
(2)设直线AC对应的函数解析式为y=kx+b,
∵直线y=kx+b经过点A(-1,2),C(1,0),
∴ 解得
∴直线AC对应的函数解析式为y=-x+1.
反比例函数与正比例函数的图象都是中心对称
图形,所以在同一坐标系中,两个函数图象的两个交
点关于原点对称.
新知小结
【中考·天水】下列给出的函数中,其图象是中心对
称图形的是( )
①函数y=x;②函数y=x2;③函数
A.①② B.②③
C.①③ D.都不是
C
巩固新知
2 对于函数 ,下列说法错误的是 ( )
A.这个函数的图象位于第一、第三象限
B.这个函数的图象既是轴对称图形又是中心对称
图形
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
C
已知P为函数 的图象上一点,且点P到原点
的距离为2,则符合条件的点P有( )
A.0个 B.2个
C.4个 D.无数个
B
如图,边长为4的正方形ABCD的对称中心是坐
标原点O,AB∥x轴,BC∥y轴,反比例函数
与 的图象均与正方形ABCD的
边相交,则图中阴影部
分的面积之和是______.
8
1.反比例函数中k的几何性质:过双曲线 (k≠0)
上任一点向两坐标轴作垂线所得的矩形面积等于|k|;
向一坐标轴作垂线且与原点连线所得的三角形面积等
于 |k|.
2.双曲线关于直线y=x和直线y=-x成轴对称.
1
知识小结
归纳新知
如图,面积为5的矩形OABC的一个顶点B在反比例函数y=
的图象上,另三点在坐标轴上,则k=______.
易错点:已知图形面积求反比例函数比例系数k的值时,易忽视图象的位置.
-5
2
易错小结
|k|
课后练习
C
【答案】C
【答案】B
【答案】B
中心
坐标原点
(-a,-b)
轴
x
-x
(a,b)
(-b,-a)
【答案】D
C
【答案】C
