2022年沪科版数学七年级下册10.3 平行线的性质 课时练习(Word版含答案)
文档属性
| 名称 | 2022年沪科版数学七年级下册10.3 平行线的性质 课时练习(Word版含答案) | 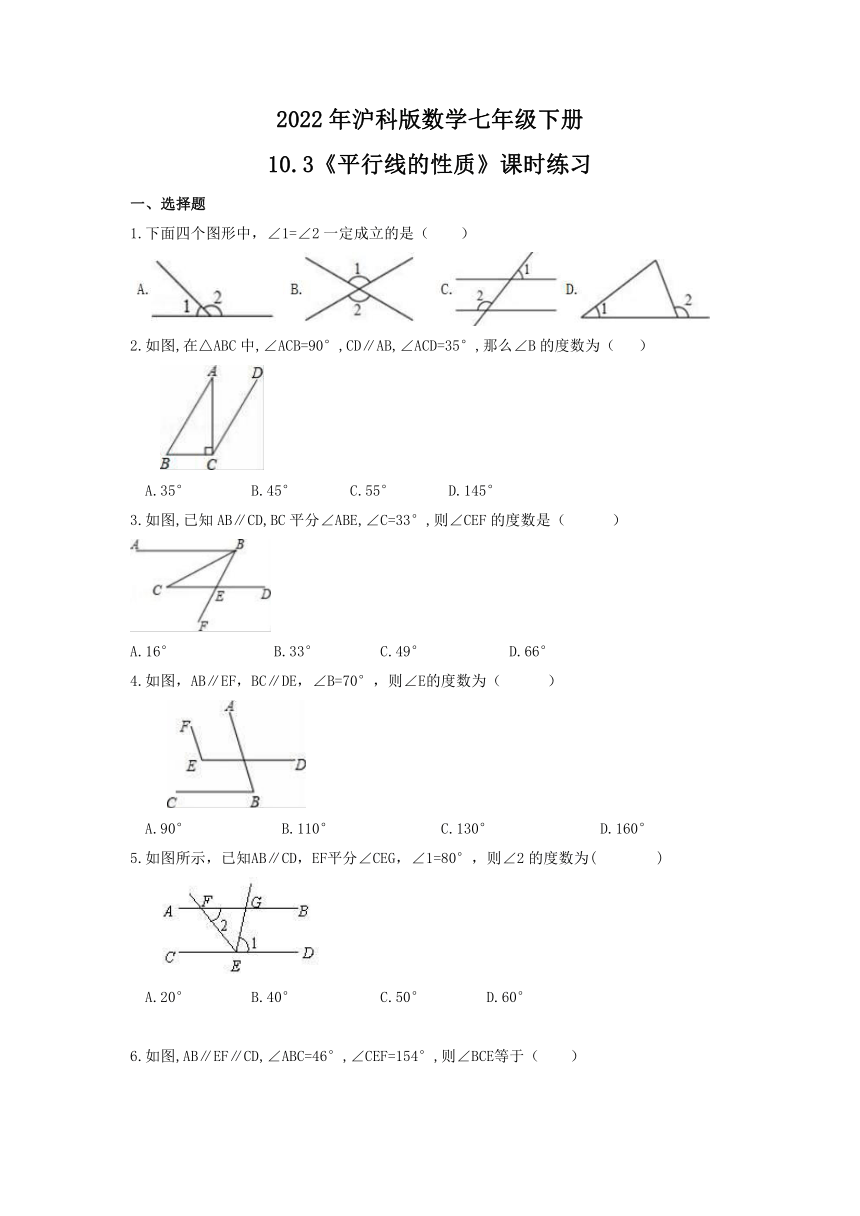 | |
| 格式 | docx | ||
| 文件大小 | 183.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 16:25:09 | ||
图片预览



文档简介
2022年沪科版数学七年级下册
10.3《平行线的性质》课时练习
一、选择题
1.下面四个图形中,∠1=∠2一定成立的是( )
2.如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=35°,那么∠B的度数为( )
A.35° B.45° C.55° D.145°
3.如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
A.16° B.33° C.49° D.66°
4.如图,AB∥EF,BC∥DE,∠B=70°,则∠E的度数为( )
A.90° B.110° C.130° D.160°
5.如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
A.20° B.40° C.50° D.60°
6.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于( )
A.23° B.16° C.20° D.26°
7.如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
A.132° B.134° C.136° D.138°
8.如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
A.40° B.50° C.70° D.80°
二、填空题
9.如图,已知AF∥EC,AB∥CD,∠A=65°,则∠C= 度.
10.在同一平面内如图,EG∥BC,CD交EG于点F,那么图中与∠1相等的角共有 个.
11.如图,AB∥CD,若∠ABE=120°,∠DCE=32°,则∠BEC= .
12.如图,AB∥CE,BF交CE于点D,DE=DF,∠F=20°,则∠B的度数为 .
13.如图,已知a//b,∠1=70°,∠2=40°,则∠3= .
14.完成下面的证明:
已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.
求证:∠EGF=90°.
证明:∵HG∥AB(已知)
∴∠1=∠3( )
又∵HG∥CD(已知)
∴∠2=∠4( )
∵AB∥CD(已知)
∴∠BEF+___________=180°( )
又∵EG平分∠BEF(已知)
∴∠1=0.5∠_____________( )
又∵FG平分∠EFD( )
∴∠2=( )∠_____________( )
∴∠1+∠2=0.5 (___________+______________)
∴∠1+∠2=( )
∴∠3+∠4=90°( )即∠EGF=90°.
三、解答题
15.如图,已知AB∥CD,CE∥BF.求证:∠C+∠B=180°.
16.如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=400,求∠2的度数.
17.如图,已知AB∥CD,∠1:∠2:∠3=1:2:3.
求证:BA平分∠EBF.
下面给出证法1.
证法1:设∠1、∠2、∠3的度数分别为x,2x,3x.
∵AB∥CD,
∴2x+3x=180°,解得x=36°
∴∠1=36°,∠2=72°,∠3=108°
∵∠EBD=180°,
∴∠EBA=72°
∴BA平分∠EBF
请阅读证法1后,找出与证法1不同的证法2,并写出证明过程.
18.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
参考答案
1.B.
2.C
3.D
4.B
5.C
6.C
7.B
8.C
9.答案为:65
10.答案为:2.
11.答案为:92°.
12.答案为:40°
13.答案为:70°
14.答案为:两直线平行,内错角相等;两直线平行,内错角相等;∠DFE,两直线平行,同旁内角互补;BEF,角平分线定义;已知,0.5, EFD,角平分线定义;∠BEF,∠EFD,等量代换.
15.证明:∵AB∥CD,CE∥BF,
∴∠CDB+∠B=180°,
∠C=∠CDB,
∴∠C+∠B=180°.
16.∠2=100°,
17.证明:∵AB∥CD,
∴∠2+∠3=180°,
∵∠1:∠2:∠3=1:2:3,
∴设∠1=x°,∠2=2x°,∠3=3x°,
∴2x+3x=180,
解得:x=36,
∴∠1=36°,∠2=72°,
∴∠EBA=180°-36°-72°=72°,
∴BA平分∠EBF.
18.解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°,
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°,
∴∠DCF=50°,
∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.
10.3《平行线的性质》课时练习
一、选择题
1.下面四个图形中,∠1=∠2一定成立的是( )
2.如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=35°,那么∠B的度数为( )
A.35° B.45° C.55° D.145°
3.如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
A.16° B.33° C.49° D.66°
4.如图,AB∥EF,BC∥DE,∠B=70°,则∠E的度数为( )
A.90° B.110° C.130° D.160°
5.如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
A.20° B.40° C.50° D.60°
6.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于( )
A.23° B.16° C.20° D.26°
7.如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
A.132° B.134° C.136° D.138°
8.如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
A.40° B.50° C.70° D.80°
二、填空题
9.如图,已知AF∥EC,AB∥CD,∠A=65°,则∠C= 度.
10.在同一平面内如图,EG∥BC,CD交EG于点F,那么图中与∠1相等的角共有 个.
11.如图,AB∥CD,若∠ABE=120°,∠DCE=32°,则∠BEC= .
12.如图,AB∥CE,BF交CE于点D,DE=DF,∠F=20°,则∠B的度数为 .
13.如图,已知a//b,∠1=70°,∠2=40°,则∠3= .
14.完成下面的证明:
已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.
求证:∠EGF=90°.
证明:∵HG∥AB(已知)
∴∠1=∠3( )
又∵HG∥CD(已知)
∴∠2=∠4( )
∵AB∥CD(已知)
∴∠BEF+___________=180°( )
又∵EG平分∠BEF(已知)
∴∠1=0.5∠_____________( )
又∵FG平分∠EFD( )
∴∠2=( )∠_____________( )
∴∠1+∠2=0.5 (___________+______________)
∴∠1+∠2=( )
∴∠3+∠4=90°( )即∠EGF=90°.
三、解答题
15.如图,已知AB∥CD,CE∥BF.求证:∠C+∠B=180°.
16.如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=400,求∠2的度数.
17.如图,已知AB∥CD,∠1:∠2:∠3=1:2:3.
求证:BA平分∠EBF.
下面给出证法1.
证法1:设∠1、∠2、∠3的度数分别为x,2x,3x.
∵AB∥CD,
∴2x+3x=180°,解得x=36°
∴∠1=36°,∠2=72°,∠3=108°
∵∠EBD=180°,
∴∠EBA=72°
∴BA平分∠EBF
请阅读证法1后,找出与证法1不同的证法2,并写出证明过程.
18.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
参考答案
1.B.
2.C
3.D
4.B
5.C
6.C
7.B
8.C
9.答案为:65
10.答案为:2.
11.答案为:92°.
12.答案为:40°
13.答案为:70°
14.答案为:两直线平行,内错角相等;两直线平行,内错角相等;∠DFE,两直线平行,同旁内角互补;BEF,角平分线定义;已知,0.5, EFD,角平分线定义;∠BEF,∠EFD,等量代换.
15.证明:∵AB∥CD,CE∥BF,
∴∠CDB+∠B=180°,
∠C=∠CDB,
∴∠C+∠B=180°.
16.∠2=100°,
17.证明:∵AB∥CD,
∴∠2+∠3=180°,
∵∠1:∠2:∠3=1:2:3,
∴设∠1=x°,∠2=2x°,∠3=3x°,
∴2x+3x=180,
解得:x=36,
∴∠1=36°,∠2=72°,
∴∠EBA=180°-36°-72°=72°,
∴BA平分∠EBF.
18.解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°,
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°,
∴∠DCF=50°,
∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.
