2021-2022学年湘教新版九年级下册数学第2章 圆单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教新版九年级下册数学第2章 圆单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 442.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 16:35:22 | ||
图片预览


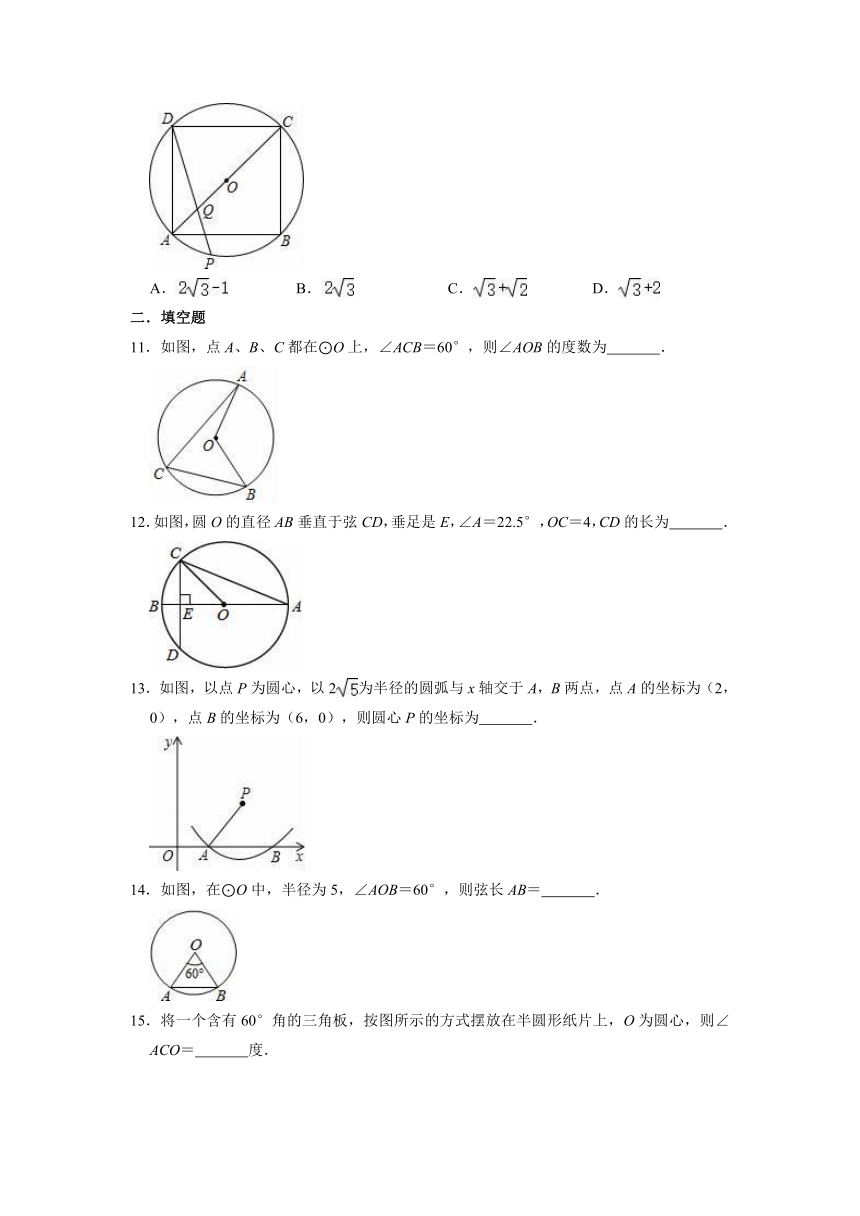

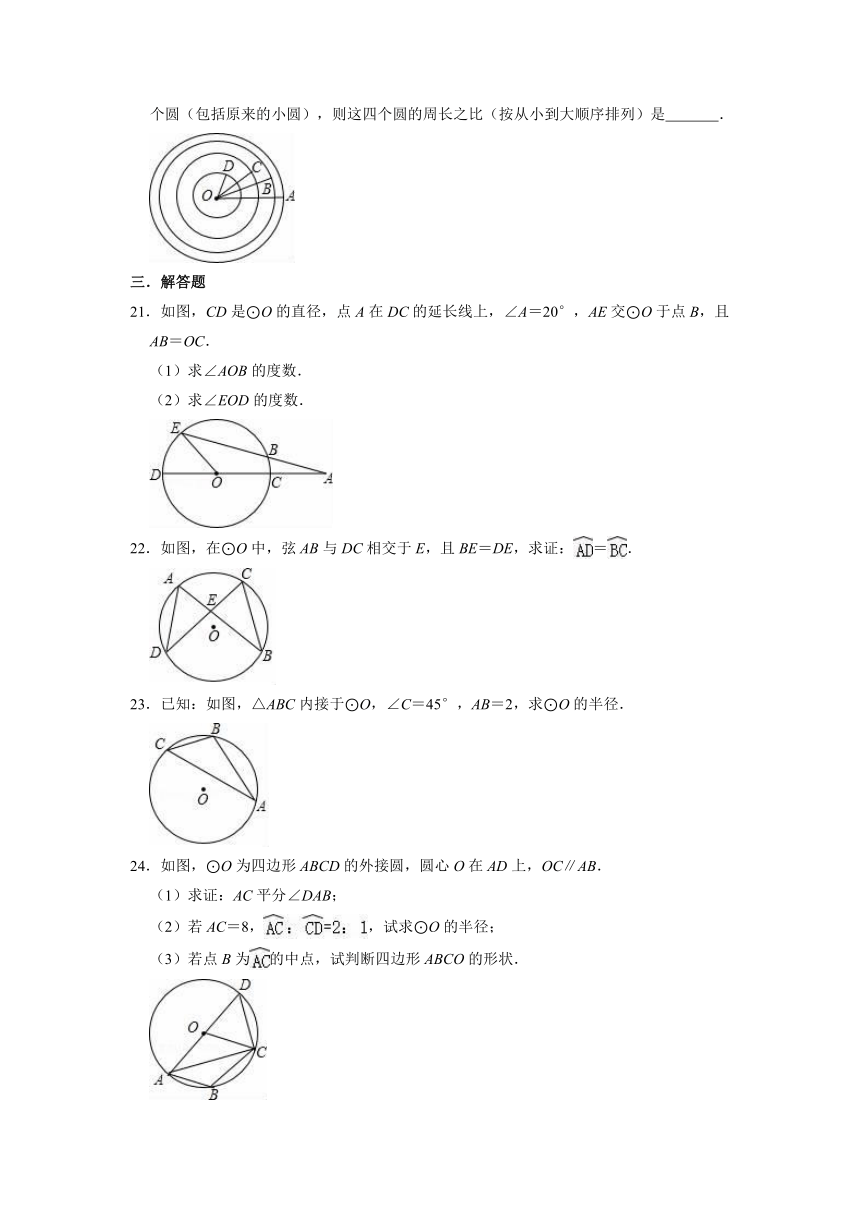
文档简介
2021-2022学年湘教新版九年级下册数学《第2章 圆》单元测试卷
一.选择题
1.下列说法,正确的是( )
A.弦是直径 B.弧是半圆
C.半圆是弧 D.过圆心的线段是直径
2.⊙O是四边形ABCD的外接圆,AC平分∠BAD,则正确结论是( )
A.AB=AD B.BC=CD C.= D.∠BCA=∠DCA
3.已知AB是半径为6的圆的一条弦,则AB的长不可能是( )
A.8 B.10 C.12 D.14
4.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
A.变大 B.变小 C.不变 D.不能确定
5.如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.则△ACF面积是( )
A. B. C. D.
6.如图,四边形ADBC内接于⊙O,∠AOB=122°,则∠ACB等于( )
A.131° B.119° C.122° D.58°
7.下列说法中,正确的个数有:(1)垂直于弦的直径平分这条弦并且平分这条弦所对的两条弧;(2)半圆是弧;(3)长度相等的弧是等弧;(4)平分弦的直径垂直于这条弦.( )
A.0个 B.1个 C.2个 D.3个
8.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.(4﹣)米 C.2米 D.(4+)米
9.如图,AD是⊙O的直径,,若∠AOB=40°,则圆周角∠BPC的度数是( )
A.40° B.50° C.60° D.70°
10.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
A. B. C. D.
二.填空题
11.如图,点A、B、C都在⊙O上,∠ACB=60°,则∠AOB的度数为 .
12.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为 .
13.如图,以点P为圆心,以2为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为 .
14.如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB= .
15.将一个含有60°角的三角板,按图所示的方式摆放在半圆形纸片上,O为圆心,则∠ACO= 度.
16.如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C、D.若==,则∠P的大小为 度.
17.如图,已知AB是⊙O的直径,PA=PB,∠P=60°,则弧CD所对的圆心角等于 度.
18.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为 度.
19.如图,在⊙O中,直径CD与弦AB相交于点E,若BE=3,AE=4,DE=2,则⊙O的半径是 .
20.把一个圆心为O,半径为r的小圆面积增加一倍,两倍,三倍,分别得到如图所示的四个圆(包括原来的小圆),则这四个圆的周长之比(按从小到大顺序排列)是 .
三.解答题
21.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数.
(2)求∠EOD的度数.
22.如图,在⊙O中,弦AB与DC相交于E,且BE=DE,求证:=.
23.已知:如图,△ABC内接于⊙O,∠C=45°,AB=2,求⊙O的半径.
24.如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.
(1)求证:AC平分∠DAB;
(2)若AC=8,,试求⊙O的半径;
(3)若点B为的中点,试判断四边形ABCO的形状.
25.如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若∠ABC=20°,求∠DEA的度数;
(2)若AC=3,AB=4,求CD的长.
26.如图,小虎牵着小狗上街,小虎的手臂与绳长共为2.5 m(手臂与拉直的绳子在一条直线上)手臂肩部距地面1.5 m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
27.如图,⊙O的半径均为R.
(1)请在图①中画出弦AB,CD,使图①为轴对称图形而不是中心对称图形;请在图②中画出弦AB,CD,使图②仍为中心对称图形;
(2)如图③,在⊙O中,AB=CD=m(0<m<2R),且AB与CD交于点E,夹角为锐角α.求四边形ACBD的面积(用含m,α的式子表示);
(3)若线段AB,CD是⊙O的两条弦,且AB=CD=R,你认为在以点A,B,C,D为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.
参考答案与试题解析
一.选择题
1.解:A、弦是连接圆上任意两点的线段,只有经过圆心的弦才是直径,不是所有的弦都是直径.故本选项错误;
B、弧是圆上任意两点间的部分,只有直径的两个端点把圆分成的两条弧是半圆,不是所有的弧都是半圆.故本选项错误;
C、圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.所以半圆是弧是正确的.
D、过圆心的弦才是直径,不是所有过圆心的线段都是直径,故本选项错误.
故选:C.
2.解:∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴=,
∴BC=CD.
故选:B.
3.解:∵圆的半径为6,
∴直径为12,
∵AB是一条弦,
∴AB的长应该小于等于12,不可能为的14,
故选:D.
4.解:∵直角△PAB中,AB2=PA2+PB2,
又∵矩形PAOB中,OP=AB,
∴PA2+PB2=AB2=OP2.
故选:C.
5.解:连OA,OB,AD,DF,过A作AG⊥CF于G点,连OE交⊙O于N,连AN,如图,
∵AB=OA=OB=1,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴弧AB的度数=60°,
又∵AB=BC=CD,
∴弧AB=弧BC=弧CD,
∴弧ABD的度数=3×60°=180°,
∴AD为⊙O的直径,∠CFA=60°,
∵AN=AF=OE=,∴AD平分NF,∴EF过O点,
∴弧FD=弧FA,
∴△FAD为等腰直角三角形,
∴∠FCA=∠FDA=45°,FA=AD=,
在Rt△AGF中,GF=AF=,AG=GF=,
在Rt△AGC中,CG=AG=,
∴S△ACF=CF AG=×(+)×=.
故选:D.
6.解:∵∠AOB=122°,
∴∠D=∠AOB=61°,
∵四边形ADBC为⊙O内接四边形,
∴∠ACB+∠D=180°,
∴∠ACB=180°﹣61°=119°.
故选:B.
7.解:(1)垂直于弦的直径平分这条弦并且平分这条弦所对的两条弧,故符合题意;
(2)半圆是弧,故符合题意;
(3)在同圆或等圆中,长度相等的弧是等弧,故不符合题意;
(4)平分弦(非直径)的直径垂直于这条弦,故不符合题意;
其中真命题的个数有2个;
故选:C.
8.解:连接OC交AB于D,连接OA,
∵点C为运行轨道的最低点,
∴OC⊥AB,
∴AD=AB=3(米),
在Rt△OAD中,OD===(米),
∴点C到弦AB所在直线的距离CD=OC﹣OD=(4﹣)米,
故选:B.
9.解:∵=,
∴∠AOB=∠COD=40°,
∴∠BOC=180°﹣40°﹣40°=100°,
∴∠BPC=∠BOC=50°,
故选:B.
10.解:如图,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,
QA=r﹣m.
在⊙O中,根据相交弦定理,得QA QC=QP QD.
即(r﹣m)(r+m)=m QD,所以QD=.
连接DO,由勾股定理,得QD2=DO2+QO2,
即,
解得
所以,
故选:D.
二.填空题
11.解:∵点A、B、C都在⊙O上,∠ACB=60°,
∴∠AOB=2∠ACB=120°,
故答案为:120°.
12.解:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=2,
∴CD=2CE=4.
故答案为4.
13.解:作PC⊥AB于C,如图,
∵点A的坐标为(2,0),点B的坐标为(6,0),
∴OA=2,OB=6,
∴AB=OB﹣OA=4,
∵PC⊥AB,
∴AC=BC=2,
在Rt△PAC中,∵PA=2,AC=2,
∴PC==4,
∵OC=OA+AC=4,
∴P点坐标为(4,4).
故答案为(4,4).
14.解:∵OA=OB=5,∠AOB=60°,
∴△OAB为等边三角形,
故AB=5.
故答案为:5.
15.解:由图可知,∠OBC=60°
∵OC=OB
∴△OBC是等边三角形
∴∠BCO=60°
则∠ACO=120°.
16.解:连接OC、OD,
∵==,
∴∠AOC=∠COD=∠DOB=60°,
∵OA=OC,OB=OD,
∴△AOC和△BOD都是等边三角形,
∴∠A=60°,∠B=60°,
∴∠P=60°,
故答案为:60.
17.解:连接OC,OD,∵PA=PB,∠P=60°,∴△PAB是等边三角形,
有∠A=∠B=60°,∵OA=OC=OD=OB,∴△COA,△DOB也是等边三角形,
∴∠COA=∠DOB=60°,∴∠COD=180°﹣∠COA﹣∠DOB=60度.
18.解:∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°,
∵=,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°,
故答案为:50.
19.解:根据相交弦定理,AE BE=CE DE,
又∵BE=3,AE=4,DE=2,
∴CE=6
∴CD=CE+DE=8
那么圆的半径等于4.
故答案为:4.
20.解:设最小的圆的面积是a,则其它三个圆的面积分别是2a,3a,4a,
所有的圆都是相似形,面积的比等于半径的比的平方,
因而半径的比是1:::2,周长的比等于相似比,即半径的比,是1:::2.
故答案为:1:::2.
三.解答题
21.解:(1)连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠AOB=∠1=∠A=20°;
(2)∵∠2=∠A+∠1,
∴∠2=2∠A,
∵OB=OE,
∴∠2=∠E,
∴∠E=2∠A,
∴∠DOE=∠A+∠E=3∠A=60°.
22.证明:在△AED和△CEB中,
,
∴△AED≌△CEB(AAS).
∴AD=BC,
∴=.
23.解:连接OB,OA,
∵∠BCA=45°,
∴∠BOA=90°,
∵OB=OA,
∴∠OBA=∠OAB=45°,
∵AB=2,
∴OB=OA=.
24.(1)证明:∵OC∥AB,
∴∠BAC=∠ACO,
∵OC=OA,
∴∠ACO=∠CAO.
∴∠CAO=∠BAC.
即:AC平分∠DAB.(2分)
(2)解:AC=8,弧AC与CD之比为2:1,
∴∠DAC=30°,
又∵AD是圆的直径,
∴∠ACD=90°
∴CD=AC tan∠DAC=,
∵∠COD=2∠DAC=60°,OD=OC,
∴△COD是等边三角形.
∴圆O的半径=CD=(2分)
(3)解:∵点B为弧AC的中点,
∴=,
∴∠BAC=∠BCA,
∵AC平分∠DAB,
∴∠OAC=∠BAC,
∴∠BAC=∠BCA=∠OAC=∠OCA.
∴OA∥BC.又OC∥AB,
∴四边形ABCO是平行四边形.
∵AO=CO,
∴四边形ABCO为菱形.(3分)
25.解:(1)如图,连接AD.
∵∠BAC=90°,∠ABC=20°,
∴∠ACD=70°.
∵AC=AD,
∴∠ACD=∠ADC=70°,
∴∠CAD=180°﹣70°﹣70°=40°,
∴∠DAE=90°﹣40°=50°.
又∵AD=AE,
∴.
(2)如图,过点A作AF⊥CD,垂足为F.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵ AF BC= AC AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
26.解:由题意可知AB=2.5m,AC=1.5m,
小狗在地平面上环绕跑圆的半径为=2.0(m),
小狗活动的区域是以2.0m为半径的圆,如图.
27.解:(1)答案不唯一,如图①、②
(2)过点A,B分别作CD的垂线,垂足分别为M,N,
∵S△ACD=CD AM=CD AE sinα,S△BCD=CD BN=CD BE sinα,
∴S四边形ACBD=S△ACD+S△BCD=CD AE sinα+CD BE sinα
=CD (AE+BE)sinα=CD AB sinα=m2 sinα.
(3)存在.分两种情况说明如下:
①当AB与CD相交时,由(2)及AB=CD=知S四边形ACBD=AB CD sinα=R2sinα,
②当AB与CD不相交时,如图④.
∵AB=CD=,OC=OD=OA=OB=R,
∴∠AOB=∠COD=90°.
而S四边形ABCD=SRt△AOB+SRt△OCD+S△AOD+S△BOC=R2+S△AOD+S△BOC
延长BO交⊙O于点E,连接EC,
则∠1+∠3=∠2+∠3=90°.
∴∠1=∠2.
∴△AOD≌△COE.
∴S△AOD=S△OCE
∴S△AOD+S△BOC=S△OCE+S△BOC=S△BCE
过点C作CH⊥BE,垂足为H,
则S△BCE=BE CH=R CH.
∴当CH=R时,S△BCE取最大值R2
综合①、②可知,当∠1=∠2=90°.
即四边形ABCD是边长为的正方形时,S四边形ABCD=R2+R2=2R2为最大值.
一.选择题
1.下列说法,正确的是( )
A.弦是直径 B.弧是半圆
C.半圆是弧 D.过圆心的线段是直径
2.⊙O是四边形ABCD的外接圆,AC平分∠BAD,则正确结论是( )
A.AB=AD B.BC=CD C.= D.∠BCA=∠DCA
3.已知AB是半径为6的圆的一条弦,则AB的长不可能是( )
A.8 B.10 C.12 D.14
4.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
A.变大 B.变小 C.不变 D.不能确定
5.如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.则△ACF面积是( )
A. B. C. D.
6.如图,四边形ADBC内接于⊙O,∠AOB=122°,则∠ACB等于( )
A.131° B.119° C.122° D.58°
7.下列说法中,正确的个数有:(1)垂直于弦的直径平分这条弦并且平分这条弦所对的两条弧;(2)半圆是弧;(3)长度相等的弧是等弧;(4)平分弦的直径垂直于这条弦.( )
A.0个 B.1个 C.2个 D.3个
8.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.(4﹣)米 C.2米 D.(4+)米
9.如图,AD是⊙O的直径,,若∠AOB=40°,则圆周角∠BPC的度数是( )
A.40° B.50° C.60° D.70°
10.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为( )
A. B. C. D.
二.填空题
11.如图,点A、B、C都在⊙O上,∠ACB=60°,则∠AOB的度数为 .
12.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为 .
13.如图,以点P为圆心,以2为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为 .
14.如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB= .
15.将一个含有60°角的三角板,按图所示的方式摆放在半圆形纸片上,O为圆心,则∠ACO= 度.
16.如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C、D.若==,则∠P的大小为 度.
17.如图,已知AB是⊙O的直径,PA=PB,∠P=60°,则弧CD所对的圆心角等于 度.
18.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为 度.
19.如图,在⊙O中,直径CD与弦AB相交于点E,若BE=3,AE=4,DE=2,则⊙O的半径是 .
20.把一个圆心为O,半径为r的小圆面积增加一倍,两倍,三倍,分别得到如图所示的四个圆(包括原来的小圆),则这四个圆的周长之比(按从小到大顺序排列)是 .
三.解答题
21.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数.
(2)求∠EOD的度数.
22.如图,在⊙O中,弦AB与DC相交于E,且BE=DE,求证:=.
23.已知:如图,△ABC内接于⊙O,∠C=45°,AB=2,求⊙O的半径.
24.如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.
(1)求证:AC平分∠DAB;
(2)若AC=8,,试求⊙O的半径;
(3)若点B为的中点,试判断四边形ABCO的形状.
25.如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若∠ABC=20°,求∠DEA的度数;
(2)若AC=3,AB=4,求CD的长.
26.如图,小虎牵着小狗上街,小虎的手臂与绳长共为2.5 m(手臂与拉直的绳子在一条直线上)手臂肩部距地面1.5 m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
27.如图,⊙O的半径均为R.
(1)请在图①中画出弦AB,CD,使图①为轴对称图形而不是中心对称图形;请在图②中画出弦AB,CD,使图②仍为中心对称图形;
(2)如图③,在⊙O中,AB=CD=m(0<m<2R),且AB与CD交于点E,夹角为锐角α.求四边形ACBD的面积(用含m,α的式子表示);
(3)若线段AB,CD是⊙O的两条弦,且AB=CD=R,你认为在以点A,B,C,D为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.
参考答案与试题解析
一.选择题
1.解:A、弦是连接圆上任意两点的线段,只有经过圆心的弦才是直径,不是所有的弦都是直径.故本选项错误;
B、弧是圆上任意两点间的部分,只有直径的两个端点把圆分成的两条弧是半圆,不是所有的弧都是半圆.故本选项错误;
C、圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.所以半圆是弧是正确的.
D、过圆心的弦才是直径,不是所有过圆心的线段都是直径,故本选项错误.
故选:C.
2.解:∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴=,
∴BC=CD.
故选:B.
3.解:∵圆的半径为6,
∴直径为12,
∵AB是一条弦,
∴AB的长应该小于等于12,不可能为的14,
故选:D.
4.解:∵直角△PAB中,AB2=PA2+PB2,
又∵矩形PAOB中,OP=AB,
∴PA2+PB2=AB2=OP2.
故选:C.
5.解:连OA,OB,AD,DF,过A作AG⊥CF于G点,连OE交⊙O于N,连AN,如图,
∵AB=OA=OB=1,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴弧AB的度数=60°,
又∵AB=BC=CD,
∴弧AB=弧BC=弧CD,
∴弧ABD的度数=3×60°=180°,
∴AD为⊙O的直径,∠CFA=60°,
∵AN=AF=OE=,∴AD平分NF,∴EF过O点,
∴弧FD=弧FA,
∴△FAD为等腰直角三角形,
∴∠FCA=∠FDA=45°,FA=AD=,
在Rt△AGF中,GF=AF=,AG=GF=,
在Rt△AGC中,CG=AG=,
∴S△ACF=CF AG=×(+)×=.
故选:D.
6.解:∵∠AOB=122°,
∴∠D=∠AOB=61°,
∵四边形ADBC为⊙O内接四边形,
∴∠ACB+∠D=180°,
∴∠ACB=180°﹣61°=119°.
故选:B.
7.解:(1)垂直于弦的直径平分这条弦并且平分这条弦所对的两条弧,故符合题意;
(2)半圆是弧,故符合题意;
(3)在同圆或等圆中,长度相等的弧是等弧,故不符合题意;
(4)平分弦(非直径)的直径垂直于这条弦,故不符合题意;
其中真命题的个数有2个;
故选:C.
8.解:连接OC交AB于D,连接OA,
∵点C为运行轨道的最低点,
∴OC⊥AB,
∴AD=AB=3(米),
在Rt△OAD中,OD===(米),
∴点C到弦AB所在直线的距离CD=OC﹣OD=(4﹣)米,
故选:B.
9.解:∵=,
∴∠AOB=∠COD=40°,
∴∠BOC=180°﹣40°﹣40°=100°,
∴∠BPC=∠BOC=50°,
故选:B.
10.解:如图,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,
QA=r﹣m.
在⊙O中,根据相交弦定理,得QA QC=QP QD.
即(r﹣m)(r+m)=m QD,所以QD=.
连接DO,由勾股定理,得QD2=DO2+QO2,
即,
解得
所以,
故选:D.
二.填空题
11.解:∵点A、B、C都在⊙O上,∠ACB=60°,
∴∠AOB=2∠ACB=120°,
故答案为:120°.
12.解:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=2,
∴CD=2CE=4.
故答案为4.
13.解:作PC⊥AB于C,如图,
∵点A的坐标为(2,0),点B的坐标为(6,0),
∴OA=2,OB=6,
∴AB=OB﹣OA=4,
∵PC⊥AB,
∴AC=BC=2,
在Rt△PAC中,∵PA=2,AC=2,
∴PC==4,
∵OC=OA+AC=4,
∴P点坐标为(4,4).
故答案为(4,4).
14.解:∵OA=OB=5,∠AOB=60°,
∴△OAB为等边三角形,
故AB=5.
故答案为:5.
15.解:由图可知,∠OBC=60°
∵OC=OB
∴△OBC是等边三角形
∴∠BCO=60°
则∠ACO=120°.
16.解:连接OC、OD,
∵==,
∴∠AOC=∠COD=∠DOB=60°,
∵OA=OC,OB=OD,
∴△AOC和△BOD都是等边三角形,
∴∠A=60°,∠B=60°,
∴∠P=60°,
故答案为:60.
17.解:连接OC,OD,∵PA=PB,∠P=60°,∴△PAB是等边三角形,
有∠A=∠B=60°,∵OA=OC=OD=OB,∴△COA,△DOB也是等边三角形,
∴∠COA=∠DOB=60°,∴∠COD=180°﹣∠COA﹣∠DOB=60度.
18.解:∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°,
∵=,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°,
故答案为:50.
19.解:根据相交弦定理,AE BE=CE DE,
又∵BE=3,AE=4,DE=2,
∴CE=6
∴CD=CE+DE=8
那么圆的半径等于4.
故答案为:4.
20.解:设最小的圆的面积是a,则其它三个圆的面积分别是2a,3a,4a,
所有的圆都是相似形,面积的比等于半径的比的平方,
因而半径的比是1:::2,周长的比等于相似比,即半径的比,是1:::2.
故答案为:1:::2.
三.解答题
21.解:(1)连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠AOB=∠1=∠A=20°;
(2)∵∠2=∠A+∠1,
∴∠2=2∠A,
∵OB=OE,
∴∠2=∠E,
∴∠E=2∠A,
∴∠DOE=∠A+∠E=3∠A=60°.
22.证明:在△AED和△CEB中,
,
∴△AED≌△CEB(AAS).
∴AD=BC,
∴=.
23.解:连接OB,OA,
∵∠BCA=45°,
∴∠BOA=90°,
∵OB=OA,
∴∠OBA=∠OAB=45°,
∵AB=2,
∴OB=OA=.
24.(1)证明:∵OC∥AB,
∴∠BAC=∠ACO,
∵OC=OA,
∴∠ACO=∠CAO.
∴∠CAO=∠BAC.
即:AC平分∠DAB.(2分)
(2)解:AC=8,弧AC与CD之比为2:1,
∴∠DAC=30°,
又∵AD是圆的直径,
∴∠ACD=90°
∴CD=AC tan∠DAC=,
∵∠COD=2∠DAC=60°,OD=OC,
∴△COD是等边三角形.
∴圆O的半径=CD=(2分)
(3)解:∵点B为弧AC的中点,
∴=,
∴∠BAC=∠BCA,
∵AC平分∠DAB,
∴∠OAC=∠BAC,
∴∠BAC=∠BCA=∠OAC=∠OCA.
∴OA∥BC.又OC∥AB,
∴四边形ABCO是平行四边形.
∵AO=CO,
∴四边形ABCO为菱形.(3分)
25.解:(1)如图,连接AD.
∵∠BAC=90°,∠ABC=20°,
∴∠ACD=70°.
∵AC=AD,
∴∠ACD=∠ADC=70°,
∴∠CAD=180°﹣70°﹣70°=40°,
∴∠DAE=90°﹣40°=50°.
又∵AD=AE,
∴.
(2)如图,过点A作AF⊥CD,垂足为F.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵ AF BC= AC AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
26.解:由题意可知AB=2.5m,AC=1.5m,
小狗在地平面上环绕跑圆的半径为=2.0(m),
小狗活动的区域是以2.0m为半径的圆,如图.
27.解:(1)答案不唯一,如图①、②
(2)过点A,B分别作CD的垂线,垂足分别为M,N,
∵S△ACD=CD AM=CD AE sinα,S△BCD=CD BN=CD BE sinα,
∴S四边形ACBD=S△ACD+S△BCD=CD AE sinα+CD BE sinα
=CD (AE+BE)sinα=CD AB sinα=m2 sinα.
(3)存在.分两种情况说明如下:
①当AB与CD相交时,由(2)及AB=CD=知S四边形ACBD=AB CD sinα=R2sinα,
②当AB与CD不相交时,如图④.
∵AB=CD=,OC=OD=OA=OB=R,
∴∠AOB=∠COD=90°.
而S四边形ABCD=SRt△AOB+SRt△OCD+S△AOD+S△BOC=R2+S△AOD+S△BOC
延长BO交⊙O于点E,连接EC,
则∠1+∠3=∠2+∠3=90°.
∴∠1=∠2.
∴△AOD≌△COE.
∴S△AOD=S△OCE
∴S△AOD+S△BOC=S△OCE+S△BOC=S△BCE
过点C作CH⊥BE,垂足为H,
则S△BCE=BE CH=R CH.
∴当CH=R时,S△BCE取最大值R2
综合①、②可知,当∠1=∠2=90°.
即四边形ABCD是边长为的正方形时,S四边形ABCD=R2+R2=2R2为最大值.
