2021-2022学年湘教新版八年级下册数学第2章四边形单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教新版八年级下册数学第2章四边形单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 464.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 16:36:13 | ||
图片预览


文档简介
2021-2022学年湘教新版八年级下册数学《第2章 四边形》单元测试卷
一.选择题
1.一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
2.正多边形的一个内角等于135°,则该多边形是正( )边形.
A.8 B.9 C.10 D.11
3.如图,方格纸中4个小正方形的边长均为2,则图中阴影部分三个小扇形的面积和为( )
A. B.π C. D.
4.下列设计的原理不是利用三角形的稳定性的是( )
A.由四边形组成的伸缩门
B.自行车的三角形车架
C.斜钉一根木条的长方形窗框
D.照相机的三脚架
5.如图,在△ABC中,AB=4,AC=5,BC=6,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( )
A.6 B.9 C.12 D.15
6.能铺满地面的正多边形的组合是( )
A.正五边形和正方形 B.正六边形和正方形
C.正八边形和正方形 D.正十边形和正方形
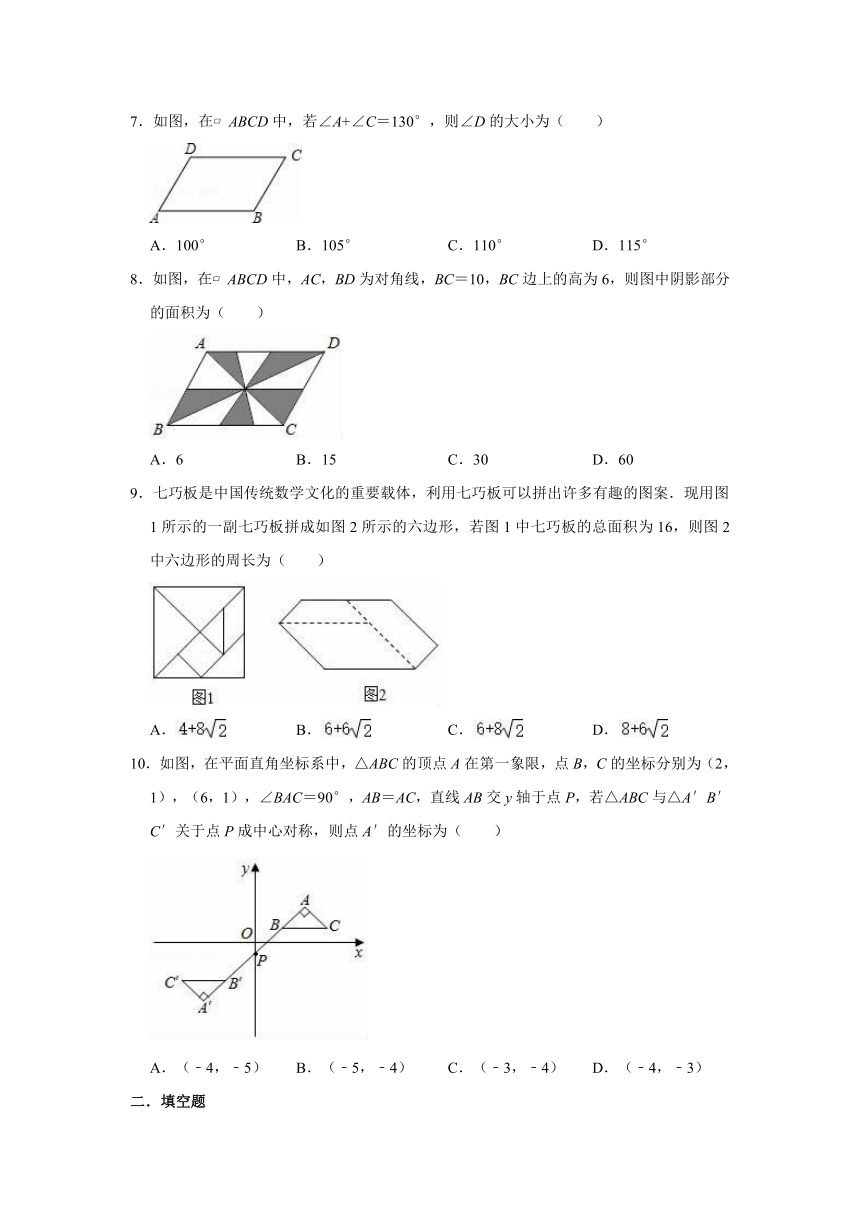
7.如图,在 ABCD中,若∠A+∠C=130°,则∠D的大小为( )
A.100° B.105° C.110° D.115°
8.如图,在 ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6 B.15 C.30 D.60
9.七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中六边形的周长为( )
A. B. C. D.
10.如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A′B′C′关于点P成中心对称,则点A′的坐标为( )
A.(﹣4,﹣5) B.(﹣5,﹣4) C.(﹣3,﹣4) D.(﹣4,﹣3)
二.填空题
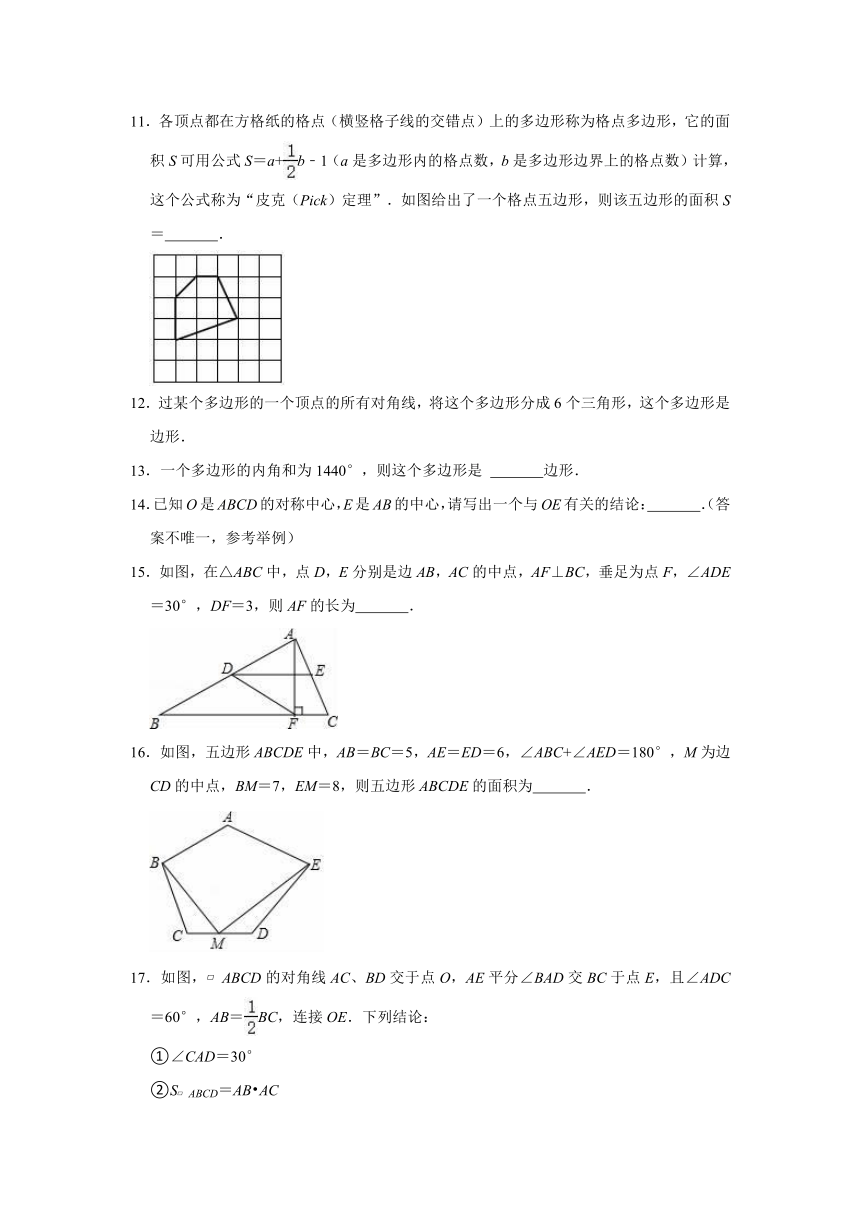
11.各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式S=a+b﹣1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积S= .
12.过某个多边形的一个顶点的所有对角线,将这个多边形分成6个三角形,这个多边形是 边形.
13.一个多边形的内角和为1440°,则这个多边形是 边形.
14.已知O是ABCD的对称中心,E是AB的中心,请写出一个与OE有关的结论: .(答案不唯一,参考举例)
15.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=3,则AF的长为 .
16.如图,五边形ABCDE中,AB=BC=5,AE=ED=6,∠ABC+∠AED=180°,M为边CD的中点,BM=7,EM=8,则五边形ABCDE的面积为 .
17.如图, ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:
①∠CAD=30°
②S ABCD=AB AC
③OB=AB
④OE=BC
成立的有 (把所有正确结论的序号都填在横线上)
18.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为 .
19.把边长为2的正方形纸片ABCD分割成如图的四块,其中点O为正方形的中心,点E,F分别为AB,AD的中点.用这四块纸片拼成与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠无缝隙),则四边形MNPQ的周长是 .
20.如图,在平行四边形ABCD中,∠ABC=135°,AD=4,AB=8,作对角线AC的垂直平分线EF,分别交对边AB、CD于点E和点F,则AE的长为 .
三.解答题
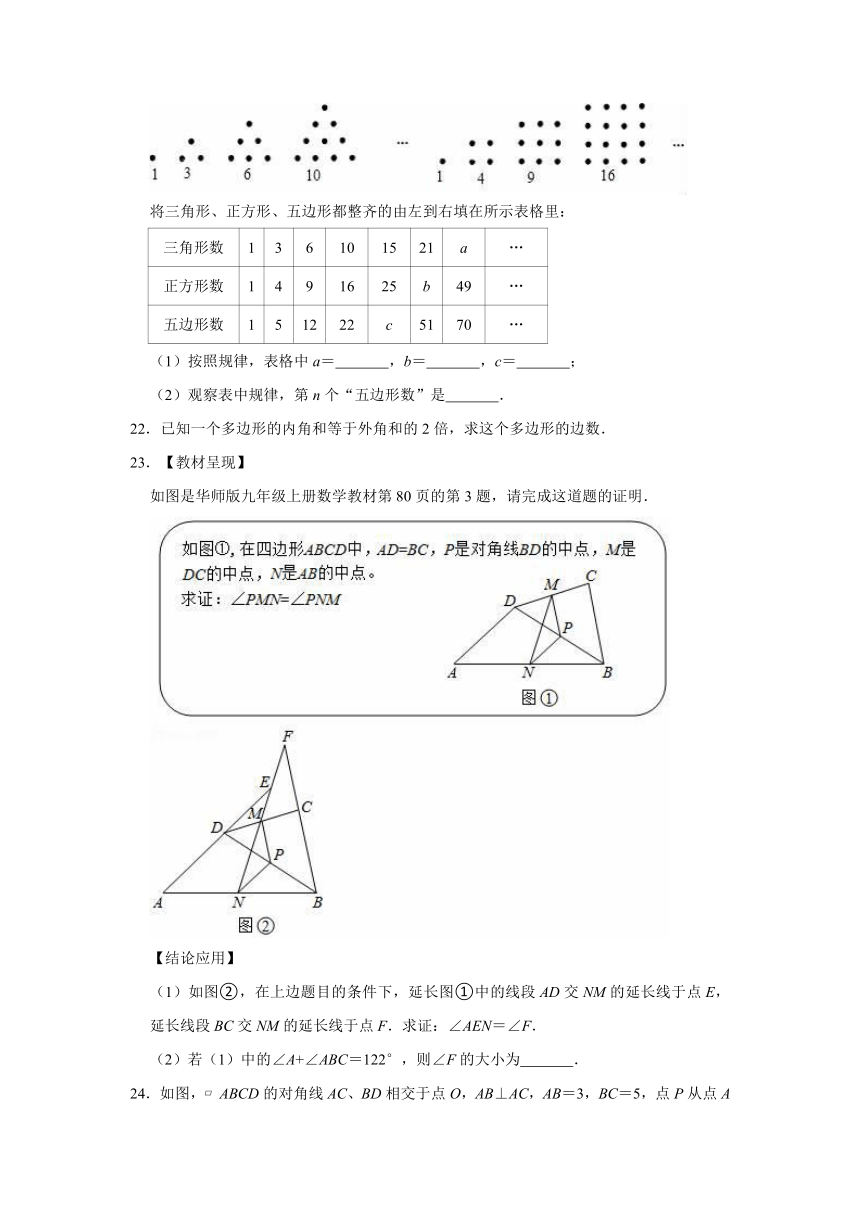
21.如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,……称为“三角形数“;把1,4,9,16,25,……称为“正方形数“.同样,可以把数1,5,12,22,……,称为“五边形数”,
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数 1 3 6 10 15 21 a …
正方形数 1 4 9 16 25 b 49 …
五边形数 1 5 12 22 c 51 70 …
(1)按照规律,表格中a= ,b= ,c= ;
(2)观察表中规律,第n个“五边形数”是 .
22.已知一个多边形的内角和等于外角和的2倍,求这个多边形的边数.
23.【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.
【结论应用】
(1)如图②,在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F.求证:∠AEN=∠F.
(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为 .
24.如图, ABCD的对角线AC、BD相交于点O,AB⊥AC,AB=3,BC=5,点P从点A出发,沿AD以每秒1个单位的速度向终点D运动.连接PO并延长交BC于点Q.设点P的运动时间为t秒.
(1)求BQ的长,(用含t的代数式表示)
(2)当四边形ABQP是平行四边形时,求t的值
(3)当点O在线段AP的垂直平分线上时,直接写出t的值.
25.如图,以n边形的n个顶点和它内部m个点作为顶点,把原n边形分割成若干个互不重叠的小三角形.观察图形,解答问题:
(1)填表:
m 个数 n 1 2 3 …
3 3 5 7 …
4 4 …
(2)填空,三角形内部有m个点,则原三角形被分割成 个不重叠的小三角形;四边形内部有m个点,则原四边形被分割成 个不重叠的小三角形;n边形内部有m个点,则原n边形被分割成 个不重叠的小三角形;
(3)若多边形内部的点的个数为多边形顶点数的五分之一,分割成互不重叠的小三角形共有2021个,求这个多边形的边数.
26.某学校艺术馆的地板由三种正多边形的小木板铺成,设这三种多边形的边数分别为x、y、z,求+的值.
27.我们把正n边形(n≥3)的各边三等分,分别以居中的那条线段为一边向外作正n边形,并去掉居中的那条线段,得到一个新的图形叫做正n边形的“扩展图形”,并将它的边数记为an.如图1,将正三角形进行上述操作后得到其“扩展图形”,且a3=12.图3、图4分别是正五边形、正六边形的“扩展图形”.
(1)如图2,在5×5的正方形网格中用较粗的虚线画有一个正方形,请在图2中用实线画出此正方形的“扩展图形”;
(2)已知a3=12,a4=20,a5=30,则图4中a6= ,根据以上规律,正n边形的“扩展图形”中an= ;(用含n的式子表示)
(3)已知=﹣,=﹣,=﹣,…,且+++…+=,则n= .
参考答案与试题解析
一.选择题
1.解:设多边形有n条边,
则n﹣3=3,解得n=6.
故多边形的边数为6.
故选:D.
2.解:外角是180﹣135=45度,
360÷45=8,
则这个多边形是八边形.
故选:A.
3.解:由图可知,∠1+∠2=90°,∠3=45°,
∵正方形的边长均为2,
∴阴影部分的面积==π.
故选:D.
4.解:由四边形组成的伸缩门是利用了四边形的不稳定性,
而A、C、D选项都是利用了三角形的稳定性,
故选:A.
5.解:∵点D,E,F分别是AB,BC,CA的中点,
∴DE=AC=2.5,AF=AC=2.5,EF=AB=2,AD=AB=2,
∴四边形ADEF的周长=AD+DE+EF+AF=9,
故选:B.
6.解:正五边形每个内角是180°﹣360°÷5=108°,正方形的每个内角是90°,108m+90n=360,n=4﹣m,显然m取任何正整数时,n不能得正整数,故不能铺满;
正方形的每个内角是90°,正六边形的每个内角是120度.90m+120n=360°,m=4﹣n,显然n取任何正整数时,m不能得正整数,故不能铺满;
正方形的每个内角是90°,正八边形的每个内角为:180°﹣360°÷8=135°,∵90°+2×135°=360°∴正八边形和正方形能铺满.
故选:C.
7.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=130°,
∴∠A=65°,
∴∠D=180°﹣∠A=115°.
故选:D.
8.解:观察并结合平行四边形的性质可知,图中下半部分的阴影面积等于上半部分的空白面积,
∴S阴影=S ABCD,
∵BC=10,BC边上的高为6,
∴S ABCD=10×6=60,
∴S阴影=×60=30.
故选:C.
9.解:由七巧板的面积是16可知:
图1中,AB=BC=4,
∴EF=2,
BF=FC=DE=CE=2,
DH=OH=OG=BG=,
∴图2的周长是+2+2++++4+2=8+6.
故选:D.
10.解:∵点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴A(4,3),
设直线AB解析式为y=kx+b,则
,
解得,
∴直线AB解析式为y=x﹣1,
令x=0,则y=﹣1,
∴P(0,﹣1),
又∵点A与点A'关于点P成中心对称,
∴点P为AA'的中点,
设A'(m,n),则=0,=﹣1,
∴m=﹣4,n=﹣5,
∴A'(﹣4,﹣5),
故选:A.
二.填空题
11.解:a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积,
通过图象可知a=4,b=6,
∴该五边形的面积S=4+×6﹣1=6,
故答案为:6.
12.解:设多边形是n边形,由对角线公式,得
n﹣2=6.
解得n=8,
故答案为:八.
13.解:设这个多边形的边数为n,
则(n﹣2)×180°=1440°,
解得:n=10,
即这个多边形是10边形,
故答案为:10.
14.解:O是ABCD的对称中心,E是AB的中心,
则AE=BE,OA=OC.
则与OE有关的结论:BC=2OE,OE∥BC.
15.解:在RT△ABF中,∵∠AFB=90°,AD=DB,DF=3,
∴AB=2DF=6,
∵AD=DB,AE=EC,
∴DE∥BC,
∴∠ADE=∠ABF=30°,
∴AF=AB=3,
故答案为:3.
16.解:如图,延长BM到点F,使FM=BM,连接BE,EF,DF,
在△BMC和△FDM中,
,
∴△BMC≌△FDM(SAS),
∴BC=DF=AB,∠C=∠CDF,
∵∠A+∠ABC+∠C+∠CDE+∠AED=(5﹣2)×180°=540°,
∵∠ABC+∠AED=180°,
∴∠A+∠C+∠CDE=360°,
∵∠CDE+∠CDF+∠EDF=360°,
∴∠A=∠EDF,
在△ABE和△DFE中,
,
∴ABE≌△DFE(SAS),
∴BE=EF,
∵BM=MF,
∴EM⊥BF,
∴五边形ABCDE的面积=S△ABE+S△BCM+S四BMDE
=S△EDF+S△MDF+S四BMDE
=S△BEF
=BF EM
=×7×2×8
=56.
故答案为:56.
17.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
∴AE=BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S ABCD=AB AC,故②正确,
∵AB=BC,OB=BD,
∵BD>BC,
∴AB≠OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
∴OE=AB,
∵AB=BC,
∴OE=BC.故④正确.
故答案为:①②④.
18.解:由题意可得阴影部分面积等于正方形面积的,即是,
5个这样的正方形重叠部分(阴影部分)的面积和为×4,
n个这样的正方形重叠部分(阴影部分)的面积和为×(n﹣1)=cm2.
故答案为: cm2.
19.解:如图所示:
图1的周长为1+2+3+2=6+2;
图2的周长为1+4+1+4=10;
图3的周长为3+5++=8+2.
故四边形MNPQ的周长是6+2或10或8+2.
故答案为:6+2或10或8+2.
20.解:如图,连接CE,过点C作CH⊥AB,交AB的延长线于H,
∵平行四边形ABCD中,∠ABC=135°,AD=4,
∴∠CBH=45°,BC=4,
又∵∠H=90°,
∴∠BCH=45°,
∴CH=BH=4,
设AE=x,则BE=8﹣x,
∵EF垂直平分AC,
∴CE=AE=x,
∵在Rt△CEH中,CH2+EH2=EC2,
∴42+(8﹣x+4)2=x2,
解得x=,
∴AE的长为.
故答案为:.
三.解答题
21.解:(1)∵前6个“三角形数”分别是:
1=、3=、6=、10=、15=、21=,
∴第n个“三角形数”是,
∴a==28.
∵前5个“正方形数”分别是:
1=12,4=22,9=32,16=42,25=52,
∴第n个“正方形数”是n2,
∴b=62=36.
∵前4个“五边形数”分别是:
1=,5=,12=,22=,
∴c==35.
(2)根据(1)中的规律得出:第n个“五边形数”是;
故答案为:.
22.解:设这个多边形的边数为x,依题意得
(x﹣2)×180=360×2
解得x=6
答:这个多边形的边数为6.
23.【教材呈现】证明:∵P是BD的中点,M是DC的中点,
∴PM=BC,
同理,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM,
【结论应用】(1)证明:∵P是BD的中点,M是DC的中点,
∴PM∥BC,
∴∠PMN=∠F,
同理,∠PNM=∠AEN,
∵∠PMN=∠PNM,
∴∠AEN=∠F;
(2)解:∵PN∥AD,
∴∠PNB=∠A,
∵∠DPN是△PNB的一个外角,
∴∠DPN=∠PNB+∠ABD=∠A+∠ABD,
∵PM∥BC,
∴∠MPD=∠DBC,
∴∠MPN=∠DPN+∠MPD=∠A+∠ABD+∠DBC=∠A+∠ABC=122°,
∵PM=PN,
∴∠PMN=×(180°﹣122°)=29°,
∴∠F=∠PMN=29°,
故答案为:29°.
24.解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠PAO=∠QCO,
∵∠AOP=∠COQ,
∴△APO≌△CQO(ASA),
∴AP=CQ=t,
∵BC=5,
∴BQ=5﹣t;
(2)∵AP∥BQ,
当AP=BQ时,四边形ABQP是平行四边形,
即t=5﹣t,
t=,
∴当t为秒时,四边形ABQP是平行四边形;
(3)t=,
方法一:如图,
Rt△ABC中,∵AB=3,BC=5,
∴AC===4,
∴AO=CO=AC=2,
∵,
∴AB AC=BC EF,
∴3×4=5×EF,
∴,
∴,
∵OE是AP的垂直平分线,
∴AE=AP=t,∠AEO=90°,
由勾股定理得:AE2+OE2=AO2,
∴,
∴t=或﹣(舍),
∴当t=秒时,点O在线段AP的垂直平分线上.
方法二:如图,连接AQ,CP,
∵AP=CQ,AP∥CQ,
∴四边形AQCP为平行四边形,
∵O在线段AP的垂直平分线上,
∴OA=OP,
∴AC=PQ,
∴四边形AQCP为矩形,
∴∠AQC=90°,
同方法一求出EF=AQ=,
∴BQ===,
∴QC=BC﹣BQ=5﹣=,
∴,
∴当t=秒时,点O在线段AP的垂直平分线上.
25.解:(1)观察图形,完成下表,
m 个数 n 1 2 3 …
3 3 5 7 …
4 4 6 8 …
故答案为:6,8;
(2)三角形内部1个点时,共分割成3部分,3=3+2(1﹣1),
三角形内部2个点时,共分割成5部分,5=3+2(2﹣1),
三角形内部3个点时,共分割成7部分,7=3+2(3﹣1),
…,
所以,三角形内部有m个点时,3+2(m﹣1)=2m+1,
四边形的4个顶点和它内部的m个点,
则分割成的不重叠的三角形的个数为:4+2(m﹣1)=2m+2,
n边形内部有m个点,则原n边形被分割成n+2(m﹣1)=2m+n﹣2个不重叠的小三角形;
故答案为:(2m+1),(2m+2),(2m+n﹣2);
(3)设这个多边形的边数为n,则内部的点的个数为n,
根据题意得,2×n+n﹣2=2021,
解得:n=1445,
答:这个多边形的边数为1445.
26.解:由题意知,这3种多边形的3个内角之和为360度,
已知正多边形的边数为x、y、z,
那么这三个多边形的内角和可表示为: ++=360,
两边都除以180得:1﹣+1﹣+1﹣=2,
两边都除以2得: +=.
27.解:(1)如图所示:
(2)图4中a6=6×7=42,根据以上规律,正n边形的“扩展图形”中an=n(n+1);(用含n的式子表示)
(3)∵=﹣,=﹣,=﹣,…,且+++…+=,
∴﹣=,
解得n=99.
故答案为:42,n(n+1);99.
一.选择题
1.一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
2.正多边形的一个内角等于135°,则该多边形是正( )边形.
A.8 B.9 C.10 D.11
3.如图,方格纸中4个小正方形的边长均为2,则图中阴影部分三个小扇形的面积和为( )
A. B.π C. D.
4.下列设计的原理不是利用三角形的稳定性的是( )
A.由四边形组成的伸缩门
B.自行车的三角形车架
C.斜钉一根木条的长方形窗框
D.照相机的三脚架
5.如图,在△ABC中,AB=4,AC=5,BC=6,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( )
A.6 B.9 C.12 D.15
6.能铺满地面的正多边形的组合是( )
A.正五边形和正方形 B.正六边形和正方形
C.正八边形和正方形 D.正十边形和正方形
7.如图,在 ABCD中,若∠A+∠C=130°,则∠D的大小为( )
A.100° B.105° C.110° D.115°
8.如图,在 ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6 B.15 C.30 D.60
9.七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中六边形的周长为( )
A. B. C. D.
10.如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A′B′C′关于点P成中心对称,则点A′的坐标为( )
A.(﹣4,﹣5) B.(﹣5,﹣4) C.(﹣3,﹣4) D.(﹣4,﹣3)
二.填空题
11.各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式S=a+b﹣1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积S= .
12.过某个多边形的一个顶点的所有对角线,将这个多边形分成6个三角形,这个多边形是 边形.
13.一个多边形的内角和为1440°,则这个多边形是 边形.
14.已知O是ABCD的对称中心,E是AB的中心,请写出一个与OE有关的结论: .(答案不唯一,参考举例)
15.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=3,则AF的长为 .
16.如图,五边形ABCDE中,AB=BC=5,AE=ED=6,∠ABC+∠AED=180°,M为边CD的中点,BM=7,EM=8,则五边形ABCDE的面积为 .
17.如图, ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:
①∠CAD=30°
②S ABCD=AB AC
③OB=AB
④OE=BC
成立的有 (把所有正确结论的序号都填在横线上)
18.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为 .
19.把边长为2的正方形纸片ABCD分割成如图的四块,其中点O为正方形的中心,点E,F分别为AB,AD的中点.用这四块纸片拼成与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠无缝隙),则四边形MNPQ的周长是 .
20.如图,在平行四边形ABCD中,∠ABC=135°,AD=4,AB=8,作对角线AC的垂直平分线EF,分别交对边AB、CD于点E和点F,则AE的长为 .
三.解答题
21.如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,……称为“三角形数“;把1,4,9,16,25,……称为“正方形数“.同样,可以把数1,5,12,22,……,称为“五边形数”,
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数 1 3 6 10 15 21 a …
正方形数 1 4 9 16 25 b 49 …
五边形数 1 5 12 22 c 51 70 …
(1)按照规律,表格中a= ,b= ,c= ;
(2)观察表中规律,第n个“五边形数”是 .
22.已知一个多边形的内角和等于外角和的2倍,求这个多边形的边数.
23.【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.
【结论应用】
(1)如图②,在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F.求证:∠AEN=∠F.
(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为 .
24.如图, ABCD的对角线AC、BD相交于点O,AB⊥AC,AB=3,BC=5,点P从点A出发,沿AD以每秒1个单位的速度向终点D运动.连接PO并延长交BC于点Q.设点P的运动时间为t秒.
(1)求BQ的长,(用含t的代数式表示)
(2)当四边形ABQP是平行四边形时,求t的值
(3)当点O在线段AP的垂直平分线上时,直接写出t的值.
25.如图,以n边形的n个顶点和它内部m个点作为顶点,把原n边形分割成若干个互不重叠的小三角形.观察图形,解答问题:
(1)填表:
m 个数 n 1 2 3 …
3 3 5 7 …
4 4 …
(2)填空,三角形内部有m个点,则原三角形被分割成 个不重叠的小三角形;四边形内部有m个点,则原四边形被分割成 个不重叠的小三角形;n边形内部有m个点,则原n边形被分割成 个不重叠的小三角形;
(3)若多边形内部的点的个数为多边形顶点数的五分之一,分割成互不重叠的小三角形共有2021个,求这个多边形的边数.
26.某学校艺术馆的地板由三种正多边形的小木板铺成,设这三种多边形的边数分别为x、y、z,求+的值.
27.我们把正n边形(n≥3)的各边三等分,分别以居中的那条线段为一边向外作正n边形,并去掉居中的那条线段,得到一个新的图形叫做正n边形的“扩展图形”,并将它的边数记为an.如图1,将正三角形进行上述操作后得到其“扩展图形”,且a3=12.图3、图4分别是正五边形、正六边形的“扩展图形”.
(1)如图2,在5×5的正方形网格中用较粗的虚线画有一个正方形,请在图2中用实线画出此正方形的“扩展图形”;
(2)已知a3=12,a4=20,a5=30,则图4中a6= ,根据以上规律,正n边形的“扩展图形”中an= ;(用含n的式子表示)
(3)已知=﹣,=﹣,=﹣,…,且+++…+=,则n= .
参考答案与试题解析
一.选择题
1.解:设多边形有n条边,
则n﹣3=3,解得n=6.
故多边形的边数为6.
故选:D.
2.解:外角是180﹣135=45度,
360÷45=8,
则这个多边形是八边形.
故选:A.
3.解:由图可知,∠1+∠2=90°,∠3=45°,
∵正方形的边长均为2,
∴阴影部分的面积==π.
故选:D.
4.解:由四边形组成的伸缩门是利用了四边形的不稳定性,
而A、C、D选项都是利用了三角形的稳定性,
故选:A.
5.解:∵点D,E,F分别是AB,BC,CA的中点,
∴DE=AC=2.5,AF=AC=2.5,EF=AB=2,AD=AB=2,
∴四边形ADEF的周长=AD+DE+EF+AF=9,
故选:B.
6.解:正五边形每个内角是180°﹣360°÷5=108°,正方形的每个内角是90°,108m+90n=360,n=4﹣m,显然m取任何正整数时,n不能得正整数,故不能铺满;
正方形的每个内角是90°,正六边形的每个内角是120度.90m+120n=360°,m=4﹣n,显然n取任何正整数时,m不能得正整数,故不能铺满;
正方形的每个内角是90°,正八边形的每个内角为:180°﹣360°÷8=135°,∵90°+2×135°=360°∴正八边形和正方形能铺满.
故选:C.
7.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=130°,
∴∠A=65°,
∴∠D=180°﹣∠A=115°.
故选:D.
8.解:观察并结合平行四边形的性质可知,图中下半部分的阴影面积等于上半部分的空白面积,
∴S阴影=S ABCD,
∵BC=10,BC边上的高为6,
∴S ABCD=10×6=60,
∴S阴影=×60=30.
故选:C.
9.解:由七巧板的面积是16可知:
图1中,AB=BC=4,
∴EF=2,
BF=FC=DE=CE=2,
DH=OH=OG=BG=,
∴图2的周长是+2+2++++4+2=8+6.
故选:D.
10.解:∵点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴A(4,3),
设直线AB解析式为y=kx+b,则
,
解得,
∴直线AB解析式为y=x﹣1,
令x=0,则y=﹣1,
∴P(0,﹣1),
又∵点A与点A'关于点P成中心对称,
∴点P为AA'的中点,
设A'(m,n),则=0,=﹣1,
∴m=﹣4,n=﹣5,
∴A'(﹣4,﹣5),
故选:A.
二.填空题
11.解:a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积,
通过图象可知a=4,b=6,
∴该五边形的面积S=4+×6﹣1=6,
故答案为:6.
12.解:设多边形是n边形,由对角线公式,得
n﹣2=6.
解得n=8,
故答案为:八.
13.解:设这个多边形的边数为n,
则(n﹣2)×180°=1440°,
解得:n=10,
即这个多边形是10边形,
故答案为:10.
14.解:O是ABCD的对称中心,E是AB的中心,
则AE=BE,OA=OC.
则与OE有关的结论:BC=2OE,OE∥BC.
15.解:在RT△ABF中,∵∠AFB=90°,AD=DB,DF=3,
∴AB=2DF=6,
∵AD=DB,AE=EC,
∴DE∥BC,
∴∠ADE=∠ABF=30°,
∴AF=AB=3,
故答案为:3.
16.解:如图,延长BM到点F,使FM=BM,连接BE,EF,DF,
在△BMC和△FDM中,
,
∴△BMC≌△FDM(SAS),
∴BC=DF=AB,∠C=∠CDF,
∵∠A+∠ABC+∠C+∠CDE+∠AED=(5﹣2)×180°=540°,
∵∠ABC+∠AED=180°,
∴∠A+∠C+∠CDE=360°,
∵∠CDE+∠CDF+∠EDF=360°,
∴∠A=∠EDF,
在△ABE和△DFE中,
,
∴ABE≌△DFE(SAS),
∴BE=EF,
∵BM=MF,
∴EM⊥BF,
∴五边形ABCDE的面积=S△ABE+S△BCM+S四BMDE
=S△EDF+S△MDF+S四BMDE
=S△BEF
=BF EM
=×7×2×8
=56.
故答案为:56.
17.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
∴AE=BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S ABCD=AB AC,故②正确,
∵AB=BC,OB=BD,
∵BD>BC,
∴AB≠OB,故③错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,
∵OA=OC,
∴OE=AB,
∵AB=BC,
∴OE=BC.故④正确.
故答案为:①②④.
18.解:由题意可得阴影部分面积等于正方形面积的,即是,
5个这样的正方形重叠部分(阴影部分)的面积和为×4,
n个这样的正方形重叠部分(阴影部分)的面积和为×(n﹣1)=cm2.
故答案为: cm2.
19.解:如图所示:
图1的周长为1+2+3+2=6+2;
图2的周长为1+4+1+4=10;
图3的周长为3+5++=8+2.
故四边形MNPQ的周长是6+2或10或8+2.
故答案为:6+2或10或8+2.
20.解:如图,连接CE,过点C作CH⊥AB,交AB的延长线于H,
∵平行四边形ABCD中,∠ABC=135°,AD=4,
∴∠CBH=45°,BC=4,
又∵∠H=90°,
∴∠BCH=45°,
∴CH=BH=4,
设AE=x,则BE=8﹣x,
∵EF垂直平分AC,
∴CE=AE=x,
∵在Rt△CEH中,CH2+EH2=EC2,
∴42+(8﹣x+4)2=x2,
解得x=,
∴AE的长为.
故答案为:.
三.解答题
21.解:(1)∵前6个“三角形数”分别是:
1=、3=、6=、10=、15=、21=,
∴第n个“三角形数”是,
∴a==28.
∵前5个“正方形数”分别是:
1=12,4=22,9=32,16=42,25=52,
∴第n个“正方形数”是n2,
∴b=62=36.
∵前4个“五边形数”分别是:
1=,5=,12=,22=,
∴c==35.
(2)根据(1)中的规律得出:第n个“五边形数”是;
故答案为:.
22.解:设这个多边形的边数为x,依题意得
(x﹣2)×180=360×2
解得x=6
答:这个多边形的边数为6.
23.【教材呈现】证明:∵P是BD的中点,M是DC的中点,
∴PM=BC,
同理,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM,
【结论应用】(1)证明:∵P是BD的中点,M是DC的中点,
∴PM∥BC,
∴∠PMN=∠F,
同理,∠PNM=∠AEN,
∵∠PMN=∠PNM,
∴∠AEN=∠F;
(2)解:∵PN∥AD,
∴∠PNB=∠A,
∵∠DPN是△PNB的一个外角,
∴∠DPN=∠PNB+∠ABD=∠A+∠ABD,
∵PM∥BC,
∴∠MPD=∠DBC,
∴∠MPN=∠DPN+∠MPD=∠A+∠ABD+∠DBC=∠A+∠ABC=122°,
∵PM=PN,
∴∠PMN=×(180°﹣122°)=29°,
∴∠F=∠PMN=29°,
故答案为:29°.
24.解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠PAO=∠QCO,
∵∠AOP=∠COQ,
∴△APO≌△CQO(ASA),
∴AP=CQ=t,
∵BC=5,
∴BQ=5﹣t;
(2)∵AP∥BQ,
当AP=BQ时,四边形ABQP是平行四边形,
即t=5﹣t,
t=,
∴当t为秒时,四边形ABQP是平行四边形;
(3)t=,
方法一:如图,
Rt△ABC中,∵AB=3,BC=5,
∴AC===4,
∴AO=CO=AC=2,
∵,
∴AB AC=BC EF,
∴3×4=5×EF,
∴,
∴,
∵OE是AP的垂直平分线,
∴AE=AP=t,∠AEO=90°,
由勾股定理得:AE2+OE2=AO2,
∴,
∴t=或﹣(舍),
∴当t=秒时,点O在线段AP的垂直平分线上.
方法二:如图,连接AQ,CP,
∵AP=CQ,AP∥CQ,
∴四边形AQCP为平行四边形,
∵O在线段AP的垂直平分线上,
∴OA=OP,
∴AC=PQ,
∴四边形AQCP为矩形,
∴∠AQC=90°,
同方法一求出EF=AQ=,
∴BQ===,
∴QC=BC﹣BQ=5﹣=,
∴,
∴当t=秒时,点O在线段AP的垂直平分线上.
25.解:(1)观察图形,完成下表,
m 个数 n 1 2 3 …
3 3 5 7 …
4 4 6 8 …
故答案为:6,8;
(2)三角形内部1个点时,共分割成3部分,3=3+2(1﹣1),
三角形内部2个点时,共分割成5部分,5=3+2(2﹣1),
三角形内部3个点时,共分割成7部分,7=3+2(3﹣1),
…,
所以,三角形内部有m个点时,3+2(m﹣1)=2m+1,
四边形的4个顶点和它内部的m个点,
则分割成的不重叠的三角形的个数为:4+2(m﹣1)=2m+2,
n边形内部有m个点,则原n边形被分割成n+2(m﹣1)=2m+n﹣2个不重叠的小三角形;
故答案为:(2m+1),(2m+2),(2m+n﹣2);
(3)设这个多边形的边数为n,则内部的点的个数为n,
根据题意得,2×n+n﹣2=2021,
解得:n=1445,
答:这个多边形的边数为1445.
26.解:由题意知,这3种多边形的3个内角之和为360度,
已知正多边形的边数为x、y、z,
那么这三个多边形的内角和可表示为: ++=360,
两边都除以180得:1﹣+1﹣+1﹣=2,
两边都除以2得: +=.
27.解:(1)如图所示:
(2)图4中a6=6×7=42,根据以上规律,正n边形的“扩展图形”中an=n(n+1);(用含n的式子表示)
(3)∵=﹣,=﹣,=﹣,…,且+++…+=,
∴﹣=,
解得n=99.
故答案为:42,n(n+1);99.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
