2021-2022学年华东师大新版八年级下册数学第17章 函数及其图象 单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大新版八年级下册数学第17章 函数及其图象 单元测试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 151.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览




文档简介
2021-2022学年华东师大新版八年级下册数学《第17章 函数及其图象》单元测试卷
一.选择题
1.若点P(a,a﹣3)在第四象限,则a的取值范围是( )
A.a<0 B.a>3 C.﹣3<a<0 D.0<a<3
2.设路程s,速度v,时间t,在关系式s=vt中,说法正确的是( )
A.当s一定时,v是常量,t是变量
B.当v一定时,t是常量,s是变量
C.当t一定时,t是常量,s,v是变量
D.当t一定时,s是常量,v是变量
3.设半径为r的圆的面积为S,则S=πr2,下列说法错误的是( )
A.变量是S和r B.常量是π和2
C.用S表示r为r= D.常量是π
4.下列各图象中,不能表示y是x的函数的是( )
A. B.
C. D.
5.在平面直角坐标系中,点P(﹣2021,2022)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如果点P(5,y)在第四象限,则y的取值范围是( )
A.y<0 B.y>0
C.y大于或等于0 D.y小于或等于0
7.函数y=的自变量x的取值范围是( )
A.x>1 B.x≥1 C.x>1且x≠2 D.x≥1且x≠2
8.按图(1)﹣(3)的方式摆放餐桌和椅子,照这样的方式继续摆放,如果摆放的餐桌为x张,摆放的椅子为y把,则y与x之间的关系式为( )
A.y=6x B.y=4x﹣2 C.y=5x﹣1 D.y=4x+2
9.变量x,y的一些对应值如下表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 4 2 0 ﹣2 ﹣4 ﹣6 …
根据表格中的数据规律,当x=7时,y的值是( )
A.﹣14 B.﹣7 C.7 D.14
10.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据,设鸭的质量为x千克,烤制时间为t分钟,估计当x=5.5时,t的值为( )
鸭的质量/千克 0.5 1 1.5 2 2.5 3 3.5 4
烤制时间/分 40 60 80 100 120 140 160 180
A.140 B.200 C.240 D.260
二.填空题
11.某水果店卖出的香蕉数量(千克)与售价(元)之间的关系如下表:
数量(千克) 0.5 1 1.5 2 2.5 3 3.5 …
售价(元) 1.5 3 4.5 6 7.5 9 10.5 …
如果卖出的香蕉数量用x(千克)表示,售价用y(元)表示,则y与x的关系式为 .
12.函数y=中,自变量x的取值范围是 .
13.在平面直角坐标系中,若点P(x﹣3,x)在第二象限,则x的取值范围为 .
14.在平面直角坐标系中,点P(m,n)在第二象限,则点Q(﹣m+1,﹣﹣n)在第 象限.
15.弹簧挂重物后会伸长,测得弹簧长度y(cm)与所挂物体质量x(kg)间有下面的关系:
x(kg) 1 2 3 4 5 …
y(cm) 8.5 9 9.5 10 10.5 …
现测得弹簧长度为14.5cm,所挂重物的质量为 kg.
16.点(2,﹣3)到x轴的距离为 .
17.若一个函数图象的对称轴是y轴,则该函数称为偶函数.那么在下列四个函数:
①y=2x;②y=;③y=x2;④y=(x﹣1)2+2中,属于偶函数的是 (只填序号).
18.根据如图所示的程序计算函数值,若输入x的值为,则输出的y值为 .
19.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是 .
20.下表为研究弹簧长度与所挂物体质量关系的实验表格.
所挂物体质量x(kg) 1 2 3 4
弹簧长度y(cm) 10 12 14 16
则当所挂物体质量为3.5kg时,弹簧比原来伸长了 cm.
三.解答题
21.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁的2倍、3倍.
(1)上述的哪些量在发生变化?自变量和因变量各是什么?
(2)某婴儿在出生时的体重是3.5kg,请把他在发育过程的体重情况填入下表:
年龄 出生时 6个月 1周岁 2周岁 6周岁 10周岁
体重/kg
(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的.
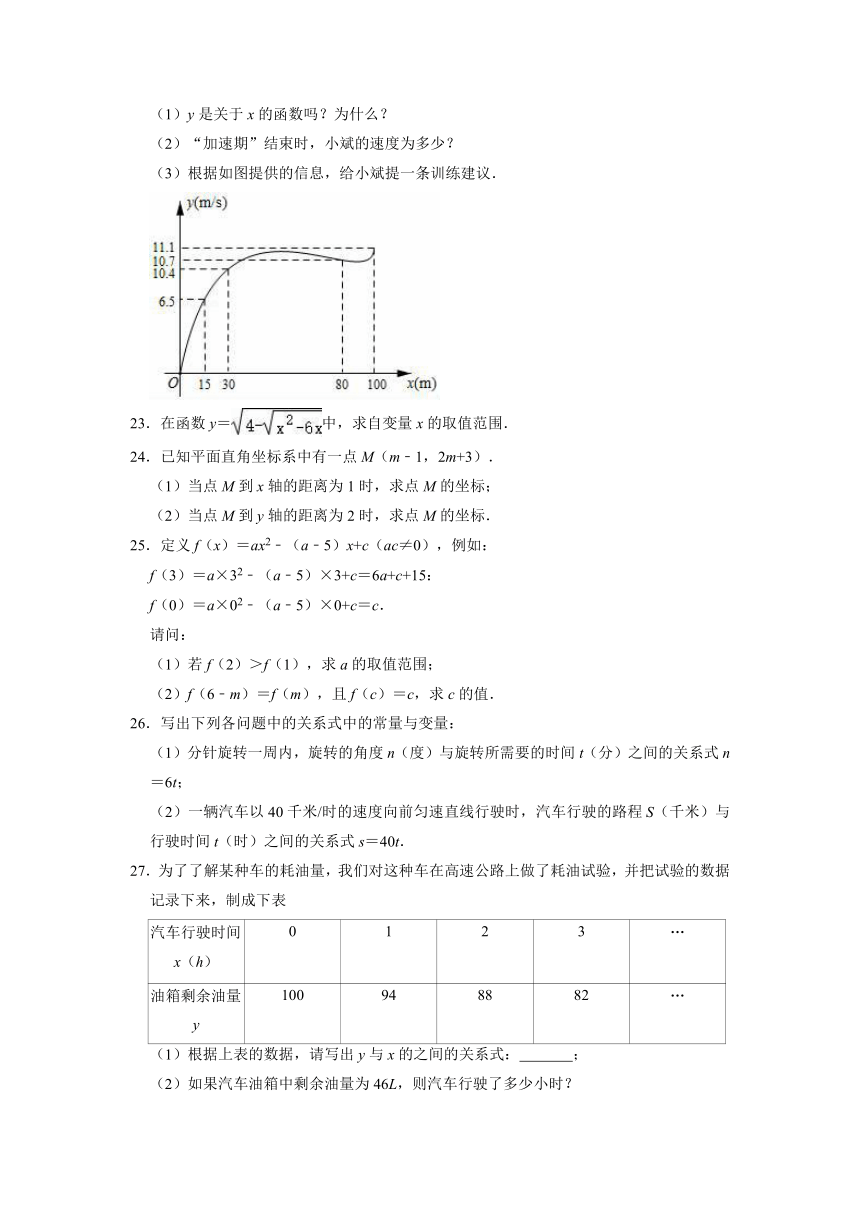
22.根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.
(1)y是关于x的函数吗?为什么?
(2)“加速期”结束时,小斌的速度为多少?
(3)根据如图提供的信息,给小斌提一条训练建议.
23.在函数y=中,求自变量x的取值范围.
24.已知平面直角坐标系中有一点M(m﹣1,2m+3).
(1)当点M到x轴的距离为1时,求点M的坐标;
(2)当点M到y轴的距离为2时,求点M的坐标.
25.定义f(x)=ax2﹣(a﹣5)x+c(ac≠0),例如:
f(3)=a×32﹣(a﹣5)×3+c=6a+c+15:
f(0)=a×02﹣(a﹣5)×0+c=c.
请问:
(1)若f(2)>f(1),求a的取值范围;
(2)f(6﹣m)=f(m),且f(c)=c,求c的值.
26.写出下列各问题中的关系式中的常量与变量:
(1)分针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t.
27.为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表
汽车行驶时间x(h) 0 1 2 3 …
油箱剩余油量y 100 94 88 82 …
(1)根据上表的数据,请写出y与x的之间的关系式: ;
(2)如果汽车油箱中剩余油量为46L,则汽车行驶了多少小时?
(3)如果该种汽车油箱只装了36L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗?为什么?
参考答案与试题解析
一.选择题
1.解:由点P(a,a﹣3)在第四象限,得
.
解得0<a<3,
故选:D.
2.解:A、当s一定时,s是常量,v、t是变量,故原题说法错误;
B、当v一定时,v是常量,t、s是变量,故原题说法错误;
C、当t一定时,t是常量,s,v是变量,说法正确;
D、当t一定时,t是常量,v、s是变量,故原题说法错误;
故选:C.
3.解:∵圆的面积S=πr2,
∴变量是S和r,常量是π,用S表示r为r=,
故说法错误的是B.
故选:B.
4.解:由图象,得
D的图象y不能有唯一的值与之对应,故D错误;
故选:D.
5.解:∵点P的坐标为P(﹣2021,2022),即横坐标小于0,纵坐标大于0,
∴点P在第二象限.
故选:B.
6.解:∵点P(5,y)在第四象限,
∴y<0.
故选:A.
7.解:根据题意得,x﹣1>0,
解得,x>1
故选:A.
8.解:有1张桌子时有6把椅子,
有2张桌子时有10把椅子,10=6+4×1,
有3张桌子时有14把椅子,14=6+4×2,
∵多一张餐桌,多放4把椅子,
∴第x张餐桌共有y=6+4(x﹣1)=4x+2.
故选:D.
9.解:由表格中变量x、y的变化关系可得y=﹣2x,
当x=7时,y=﹣2×7=﹣14,
故选:A.
10.解:由表格数据知t与x的函数表达式为:t=40+40(x﹣0.5)
=40x+20.
∴当x=5.5时,t=40×5.5+20=240(分钟).
故选:C.
二.填空题
11.解:根据表格可知香蕉的单价为3元/千克,则y=3x.
故答案为:y=3x.
12.解:根据题意得,x﹣2≥0且x≠0,
解得x≥2且x≠0,
所以,自变量x的取值范围是x≥2.
故答案为:x≥2.
13.解:∵点P(x﹣3,x)在第二象限,
∴,
解不等式①得,x<3,
所以不等式组的解集是0<x<3.
故答案为:0<x<3.
14.解:∵点P(m,n)是第二象限的点,
∴m<0、n>0,
∴﹣m>0,﹣n<0,
∴﹣m+1>0,﹣﹣n<0,
∴点Q的坐标在第四象限.
故答案为:四.
15.解:由表格可知弹簧长度y(cm)与所挂物体质量x(kg)间满足一次函数,
设y=kx+b,
∴,
∴,
∴y=0.5x+8,
当y=14.5时,x=13,
故答案为13;
16.解:点(2,﹣3)到x轴的距离为|﹣3|=3.
故答案为:3.
17.解:①y=2x,是正比例函数,函数图象的对称轴不是y轴,错误;
②y=是反比例函数,函数图象的对称轴不是y轴,错误;
③y=x2是抛物线,对称轴是y轴,是偶函数,正确;
④y=(x﹣1)2+2对称轴是直线x=1,错误.
故属于偶函数的是③.
18.解:x=时,y=﹣x+2=﹣+2=.
故答案为:.
19.解:在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是t,
故答案为:t.
20.解:设弹簧长度y与所挂物体质量x之间的关系式为y=kx+b,
将x=1,y=10与x=2,y=12分别代入解析式中可得:
,
解得,
∴y=2x+8,
当x=0时y=8,即弹簧原来长度为8cm,
x=3.5时,y=15,
15﹣8=7(cm),
故答案为:7.
三.解答题
21.解:(1)年龄在逐渐变大,体重在逐渐变重,年龄是自变量,体重是因变量;
(2)
(3)10周岁前的体重随年龄的增长而增大,从刚出生到六个月生长的最快.
22.解:(1)y是x的函数,在这个变化过程中,对于x的每一个确定的值,y都有唯一确定的值与之对应.
(2)“加速期”结束时,小斌的速度为10.4m/s.
(3)答案不唯一.例如:根据图象信息,小斌在80米左右时速度下降明显,建议增加耐力训练,提高成绩.
23.解:根据题意得:,
解得:﹣2≤x≤0或6≤x≤8.
故自变量x的取值范围是﹣2≤x≤0或6≤x≤8.
24.解:(1)∵|2m+3|=1,
∴2m+3=1或2m+3=﹣1,
解得:m=﹣1或m=﹣2,
∴点M的坐标是(﹣2,1)或(﹣3,﹣1);
(2)∵|m﹣1|=2,
∴m﹣1=2或m﹣1=﹣2,
解得:m=3或m=﹣1,
∴点M的坐标是:(2,9)或(﹣2,1).
25.解:(1)∵f(x)=ax2﹣(a﹣5)x+c,
∴f(2)=a×22﹣(a﹣5)×2+c=2a+10+c,
f(1)=a×12﹣(a﹣5)×1+c=5+c,
∵f(2)>f(1),
∴2a+10+c>5+c,
∴a>﹣;
(2)f(6﹣m)=f(m),
∴x=3是对称轴,
∴=3,
∴a=﹣1,
∴f(x)=﹣x2+6x+c,
∵f(c)=c,
∴﹣c2+6c+c=c,
∴c=0或c=6,
∵ac≠0,
∴c=6.
26.解:(1)常量:6;变量:n,t.
(2)常量:40;变量:s,t.
27.解:(1)由表格可知,开始油箱中的油为100L,每行驶1小时,油量减少6L,
所以y=100﹣6x,
故答案为:y=100﹣6x.
(2)当y=46时,100﹣6x=46,
解得:x=9,
即汽车行驶了9小时;
(3)在中途不加油的情况下不能从高速公路起点开到高速公路终点,理由如下:
∵700÷100=7(小时),
7×6=42(L),
36L<42L,
∴在中途不加油的情况下不能从高速公路起点开到高速公路终点.
一.选择题
1.若点P(a,a﹣3)在第四象限,则a的取值范围是( )
A.a<0 B.a>3 C.﹣3<a<0 D.0<a<3
2.设路程s,速度v,时间t,在关系式s=vt中,说法正确的是( )
A.当s一定时,v是常量,t是变量
B.当v一定时,t是常量,s是变量
C.当t一定时,t是常量,s,v是变量
D.当t一定时,s是常量,v是变量
3.设半径为r的圆的面积为S,则S=πr2,下列说法错误的是( )
A.变量是S和r B.常量是π和2
C.用S表示r为r= D.常量是π
4.下列各图象中,不能表示y是x的函数的是( )
A. B.
C. D.
5.在平面直角坐标系中,点P(﹣2021,2022)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如果点P(5,y)在第四象限,则y的取值范围是( )
A.y<0 B.y>0
C.y大于或等于0 D.y小于或等于0
7.函数y=的自变量x的取值范围是( )
A.x>1 B.x≥1 C.x>1且x≠2 D.x≥1且x≠2
8.按图(1)﹣(3)的方式摆放餐桌和椅子,照这样的方式继续摆放,如果摆放的餐桌为x张,摆放的椅子为y把,则y与x之间的关系式为( )
A.y=6x B.y=4x﹣2 C.y=5x﹣1 D.y=4x+2
9.变量x,y的一些对应值如下表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 4 2 0 ﹣2 ﹣4 ﹣6 …
根据表格中的数据规律,当x=7时,y的值是( )
A.﹣14 B.﹣7 C.7 D.14
10.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据,设鸭的质量为x千克,烤制时间为t分钟,估计当x=5.5时,t的值为( )
鸭的质量/千克 0.5 1 1.5 2 2.5 3 3.5 4
烤制时间/分 40 60 80 100 120 140 160 180
A.140 B.200 C.240 D.260
二.填空题
11.某水果店卖出的香蕉数量(千克)与售价(元)之间的关系如下表:
数量(千克) 0.5 1 1.5 2 2.5 3 3.5 …
售价(元) 1.5 3 4.5 6 7.5 9 10.5 …
如果卖出的香蕉数量用x(千克)表示,售价用y(元)表示,则y与x的关系式为 .
12.函数y=中,自变量x的取值范围是 .
13.在平面直角坐标系中,若点P(x﹣3,x)在第二象限,则x的取值范围为 .
14.在平面直角坐标系中,点P(m,n)在第二象限,则点Q(﹣m+1,﹣﹣n)在第 象限.
15.弹簧挂重物后会伸长,测得弹簧长度y(cm)与所挂物体质量x(kg)间有下面的关系:
x(kg) 1 2 3 4 5 …
y(cm) 8.5 9 9.5 10 10.5 …
现测得弹簧长度为14.5cm,所挂重物的质量为 kg.
16.点(2,﹣3)到x轴的距离为 .
17.若一个函数图象的对称轴是y轴,则该函数称为偶函数.那么在下列四个函数:
①y=2x;②y=;③y=x2;④y=(x﹣1)2+2中,属于偶函数的是 (只填序号).
18.根据如图所示的程序计算函数值,若输入x的值为,则输出的y值为 .
19.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是 .
20.下表为研究弹簧长度与所挂物体质量关系的实验表格.
所挂物体质量x(kg) 1 2 3 4
弹簧长度y(cm) 10 12 14 16
则当所挂物体质量为3.5kg时,弹簧比原来伸长了 cm.
三.解答题
21.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁的2倍、3倍.
(1)上述的哪些量在发生变化?自变量和因变量各是什么?
(2)某婴儿在出生时的体重是3.5kg,请把他在发育过程的体重情况填入下表:
年龄 出生时 6个月 1周岁 2周岁 6周岁 10周岁
体重/kg
(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的.
22.根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.
(1)y是关于x的函数吗?为什么?
(2)“加速期”结束时,小斌的速度为多少?
(3)根据如图提供的信息,给小斌提一条训练建议.
23.在函数y=中,求自变量x的取值范围.
24.已知平面直角坐标系中有一点M(m﹣1,2m+3).
(1)当点M到x轴的距离为1时,求点M的坐标;
(2)当点M到y轴的距离为2时,求点M的坐标.
25.定义f(x)=ax2﹣(a﹣5)x+c(ac≠0),例如:
f(3)=a×32﹣(a﹣5)×3+c=6a+c+15:
f(0)=a×02﹣(a﹣5)×0+c=c.
请问:
(1)若f(2)>f(1),求a的取值范围;
(2)f(6﹣m)=f(m),且f(c)=c,求c的值.
26.写出下列各问题中的关系式中的常量与变量:
(1)分针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t.
27.为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表
汽车行驶时间x(h) 0 1 2 3 …
油箱剩余油量y 100 94 88 82 …
(1)根据上表的数据,请写出y与x的之间的关系式: ;
(2)如果汽车油箱中剩余油量为46L,则汽车行驶了多少小时?
(3)如果该种汽车油箱只装了36L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗?为什么?
参考答案与试题解析
一.选择题
1.解:由点P(a,a﹣3)在第四象限,得
.
解得0<a<3,
故选:D.
2.解:A、当s一定时,s是常量,v、t是变量,故原题说法错误;
B、当v一定时,v是常量,t、s是变量,故原题说法错误;
C、当t一定时,t是常量,s,v是变量,说法正确;
D、当t一定时,t是常量,v、s是变量,故原题说法错误;
故选:C.
3.解:∵圆的面积S=πr2,
∴变量是S和r,常量是π,用S表示r为r=,
故说法错误的是B.
故选:B.
4.解:由图象,得
D的图象y不能有唯一的值与之对应,故D错误;
故选:D.
5.解:∵点P的坐标为P(﹣2021,2022),即横坐标小于0,纵坐标大于0,
∴点P在第二象限.
故选:B.
6.解:∵点P(5,y)在第四象限,
∴y<0.
故选:A.
7.解:根据题意得,x﹣1>0,
解得,x>1
故选:A.
8.解:有1张桌子时有6把椅子,
有2张桌子时有10把椅子,10=6+4×1,
有3张桌子时有14把椅子,14=6+4×2,
∵多一张餐桌,多放4把椅子,
∴第x张餐桌共有y=6+4(x﹣1)=4x+2.
故选:D.
9.解:由表格中变量x、y的变化关系可得y=﹣2x,
当x=7时,y=﹣2×7=﹣14,
故选:A.
10.解:由表格数据知t与x的函数表达式为:t=40+40(x﹣0.5)
=40x+20.
∴当x=5.5时,t=40×5.5+20=240(分钟).
故选:C.
二.填空题
11.解:根据表格可知香蕉的单价为3元/千克,则y=3x.
故答案为:y=3x.
12.解:根据题意得,x﹣2≥0且x≠0,
解得x≥2且x≠0,
所以,自变量x的取值范围是x≥2.
故答案为:x≥2.
13.解:∵点P(x﹣3,x)在第二象限,
∴,
解不等式①得,x<3,
所以不等式组的解集是0<x<3.
故答案为:0<x<3.
14.解:∵点P(m,n)是第二象限的点,
∴m<0、n>0,
∴﹣m>0,﹣n<0,
∴﹣m+1>0,﹣﹣n<0,
∴点Q的坐标在第四象限.
故答案为:四.
15.解:由表格可知弹簧长度y(cm)与所挂物体质量x(kg)间满足一次函数,
设y=kx+b,
∴,
∴,
∴y=0.5x+8,
当y=14.5时,x=13,
故答案为13;
16.解:点(2,﹣3)到x轴的距离为|﹣3|=3.
故答案为:3.
17.解:①y=2x,是正比例函数,函数图象的对称轴不是y轴,错误;
②y=是反比例函数,函数图象的对称轴不是y轴,错误;
③y=x2是抛物线,对称轴是y轴,是偶函数,正确;
④y=(x﹣1)2+2对称轴是直线x=1,错误.
故属于偶函数的是③.
18.解:x=时,y=﹣x+2=﹣+2=.
故答案为:.
19.解:在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是t,
故答案为:t.
20.解:设弹簧长度y与所挂物体质量x之间的关系式为y=kx+b,
将x=1,y=10与x=2,y=12分别代入解析式中可得:
,
解得,
∴y=2x+8,
当x=0时y=8,即弹簧原来长度为8cm,
x=3.5时,y=15,
15﹣8=7(cm),
故答案为:7.
三.解答题
21.解:(1)年龄在逐渐变大,体重在逐渐变重,年龄是自变量,体重是因变量;
(2)
(3)10周岁前的体重随年龄的增长而增大,从刚出生到六个月生长的最快.
22.解:(1)y是x的函数,在这个变化过程中,对于x的每一个确定的值,y都有唯一确定的值与之对应.
(2)“加速期”结束时,小斌的速度为10.4m/s.
(3)答案不唯一.例如:根据图象信息,小斌在80米左右时速度下降明显,建议增加耐力训练,提高成绩.
23.解:根据题意得:,
解得:﹣2≤x≤0或6≤x≤8.
故自变量x的取值范围是﹣2≤x≤0或6≤x≤8.
24.解:(1)∵|2m+3|=1,
∴2m+3=1或2m+3=﹣1,
解得:m=﹣1或m=﹣2,
∴点M的坐标是(﹣2,1)或(﹣3,﹣1);
(2)∵|m﹣1|=2,
∴m﹣1=2或m﹣1=﹣2,
解得:m=3或m=﹣1,
∴点M的坐标是:(2,9)或(﹣2,1).
25.解:(1)∵f(x)=ax2﹣(a﹣5)x+c,
∴f(2)=a×22﹣(a﹣5)×2+c=2a+10+c,
f(1)=a×12﹣(a﹣5)×1+c=5+c,
∵f(2)>f(1),
∴2a+10+c>5+c,
∴a>﹣;
(2)f(6﹣m)=f(m),
∴x=3是对称轴,
∴=3,
∴a=﹣1,
∴f(x)=﹣x2+6x+c,
∵f(c)=c,
∴﹣c2+6c+c=c,
∴c=0或c=6,
∵ac≠0,
∴c=6.
26.解:(1)常量:6;变量:n,t.
(2)常量:40;变量:s,t.
27.解:(1)由表格可知,开始油箱中的油为100L,每行驶1小时,油量减少6L,
所以y=100﹣6x,
故答案为:y=100﹣6x.
(2)当y=46时,100﹣6x=46,
解得:x=9,
即汽车行驶了9小时;
(3)在中途不加油的情况下不能从高速公路起点开到高速公路终点,理由如下:
∵700÷100=7(小时),
7×6=42(L),
36L<42L,
∴在中途不加油的情况下不能从高速公路起点开到高速公路终点.
