2021-2022学年华东师大新版九年级下册数学-第27章 圆 单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大新版九年级下册数学-第27章 圆 单元测试卷(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 347.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览

文档简介
2021-2022学年华东师大新版九年级下册数学《第27章 圆》单元测试卷
一.选择题
1.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为( )
A. B. C.24 D.16
2.如图,AB是⊙O的直径,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则∠DAC等于( )
A.15° B.30° C.45° D.60°
3.下列语句中不正确的有( )
①相等的圆心角所对的弧相等;
②平分弦的直径垂直于弦;
③圆是轴对称图形,任何一条直径所在直线都是它的对称轴;
④长度相等的两条弧是等弧.
A.3个 B.2个 C.1个 D.以上都不对
4.如图,点A,B,C都在⊙O上,若∠C=34°,则∠AOB为( )
A.34° B.56° C.60° D.68°
5.已知AB是半径为5的圆的一条弦,则AB的长不可能是( )
A.4 B.8 C.10 D.12
6.如图,AB是半圆O的直径,∠BAC=20°,则∠D的度数是( )
A.70° B.100° C.110° D.120°
7.对下列生活现象的解释其数学原理运用错误的是( )
A.把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理
B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理
C.将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理
D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理
8.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是( )
A.12寸 B.24寸 C.13寸 D.26寸
9.P为⊙O内一点,OP=3,⊙O半径为5,则经过P点的最短弦长为( )
A.5 B.6 C.8 D.10
10.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么这条圆弧所在的圆的圆心为图中的( )
A.M B.P C.Q D.R
二.填空题
11.如图,点A、B在⊙O上,且AB=BO.∠ABO的平分线与AO相交于点C,若AC=3,则⊙O的周长为 .(结果保留π)
12.如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,∠ADB=45°,则⊙O的半径长为 .
13.如图,⊙O的直径CD为6cm,OA,OB都是⊙O的半径,∠AOD=2∠AOB=60°,点P在直径CD上移动,则AP+BP的最小值为 .
14.如图,在Rt△ABC中,AC=3,BC=4,分别以它的三边为直径向上作三个半圆,则阴影部分面积为 .(不取近似值)
15.在直角坐标系中,横坐标和纵坐标都是整数的点称为格点.已知一个圆的圆心在原点,半径等于5,那么这个圆上的格点有 个.
16.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE= .
17.如图,点A在⊙O上,弦BC垂直平分OA,垂足为D.若OA=4,则BC的长为 .
18.《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有圆材埋壁中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材埋在墙壁中,不知其大小用锯子去锯这个木材,锯口深1寸(即DE=1寸),锯道长1尺(即弦AB=1尺),问这块圆形木材的直径是多少?”该问题的答案是 (注:1尺=10寸)
19.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 度.
20.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 .
三.解答题
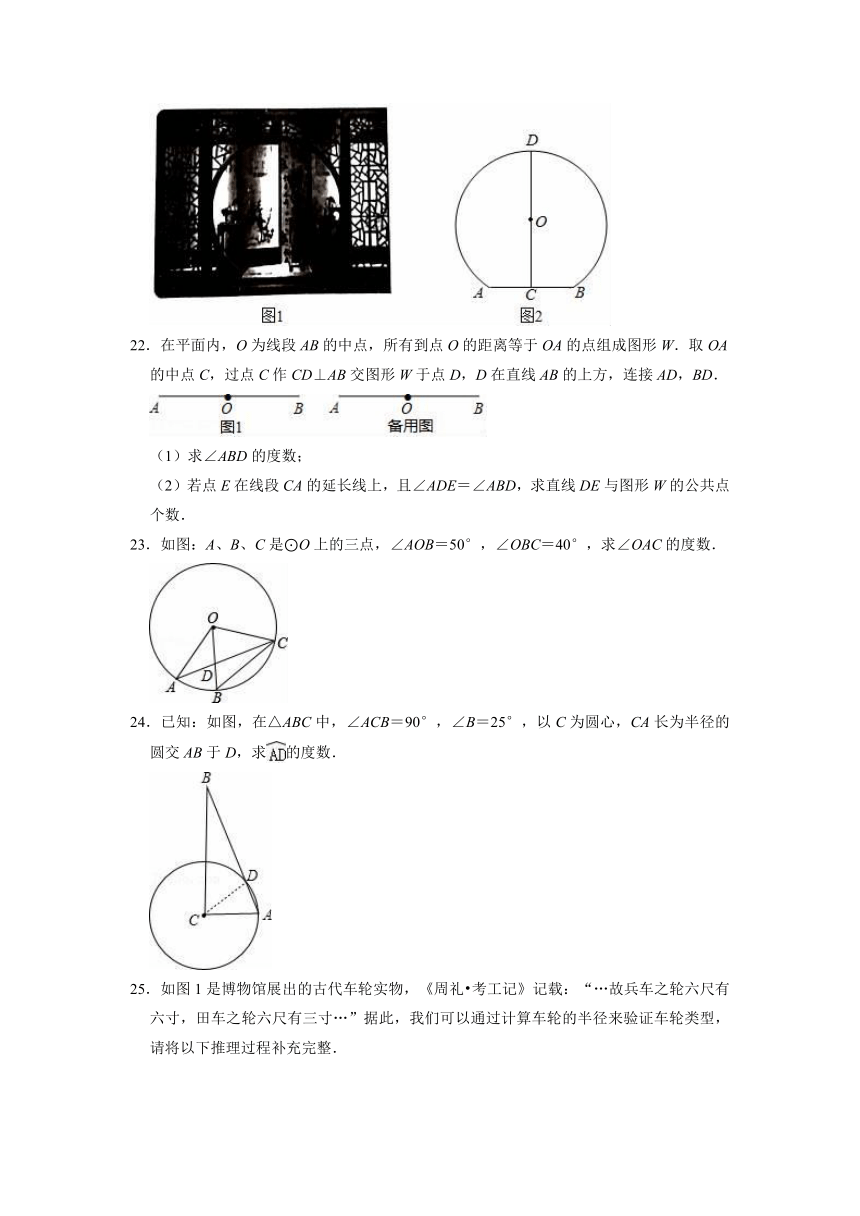
21.如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端AB=18分米,C为AB中点,D为拱门最高点,圆心O在线段CD上,CD=27分米,求拱门所在圆的半径.
22.在平面内,O为线段AB的中点,所有到点O的距离等于OA的点组成图形W.取OA的中点C,过点C作CD⊥AB交图形W于点D,D在直线AB的上方,连接AD,BD.
(1)求∠ABD的度数;
(2)若点E在线段CA的延长线上,且∠ADE=∠ABD,求直线DE与图形W的公共点个数.
23.如图:A、B、C是⊙O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
24.已知:如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,CA长为半径的圆交AB于D,求的度数.
25.如图1是博物馆展出的古代车轮实物,《周礼 考工记》记载:“…故兵车之轮六尺有六寸,田车之轮六尺有三寸…”据此,我们可以通过计算车轮的半径来验证车轮类型,请将以下推理过程补充完整.
如图2所示,在车轮上取A、B两点,设所在圆的圆心为O,半径为rcm.
作弦AB的垂线OC,D为垂足,则D是AB的中点.其推理依据是: .
经测量:AB=90cm,CD=15cm,则AD= cm;
用含r的代数式表示OD,OD= cm.
在Rt△OAD中,由勾股定理可列出关于r的方程:
r2= ,
解得r=75.
通过单位换算,得到车轮直径约为六尺六寸,可验证此车轮为兵车之轮.
26.如图,⊙O的半径OB=5cm,AB是⊙O的弦,点C是AB延长线上一点,且∠OCA=30°,OC=8cm,求AB的长.
27.已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
参考答案与试题解析
一.选择题
1.解:如图,过点O作OC⊥AB,垂足为C,
∵∠AOB=90°,∠A=∠AOC=45°,
∴OC=AC,
∵CO=4,
∴AC=4,
∴OA=4,
∴⊙O的直径长为8.
故选:B.
2.解:∵OA=OC,
∴∠CAO=∠ACO,
∵AD∥OC,
∴∠DAC=∠ACO,
∴∠DAC=∠CAB,
∵∠DAB=60°,
∴∠DAC=∠DAB=30°,
故选:B.
3.解:在同圆或等圆中,相等的圆心角所对的弧相等,所以①的说法错误;
平分弦(非直径)的直径垂直于弦,所以②的说法错误;
圆是轴对称图形,任何一条直径所在直线都是它的对称轴,所以③的说法正确;
能完全重合的两条弧是等弧,所以④的说法错误.
故选:A.
4.解:∵∠C=34°,
∴∠AOB=2∠C=68°.
故选:D.
5.解:因为圆中最长的弦为直径,所以弦长L≤10.
故选:D.
6.解:连接BC,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°,
∵∠BAC=20°,
∴∠ABC=90°﹣20°=70°,
∵圆内接四边形的对角互补,
∴∠D+∠ABC=180°,
∴∠D=180°﹣70°=110°,
故选:C.
7.解:A、把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理,正确;
B、木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“两点确定一条直线”的原理,故错误;
C、将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理,正确;
D、将车轮设计为圆形是运用了“圆的旋转对称性”的原理,正确,
故选:B.
8.解:连接OA,
∵AB⊥CD,且AB=10寸,
∴AE=BE=5寸,
设圆O的半径OA的长为x,则OC=OD=x,
∵CE=1,
∴OE=x﹣1,
在直角三角形AOE中,根据勾股定理得:
x2﹣(x﹣1)2=52,化简得:x2﹣x2+2x﹣1=25,
即2x=26,
∴CD=26(寸).
故选:D.
9.解:
如图,过P作AB⊥OP,交⊙O于A、B,则线段AB是过P点的最短的弦,连接OA,
则∠OPA=90°,
由勾股定理得:AP===4,
∵OP⊥AB,OP过圆心O,
∴BP=AP=4,
即AB=4+4=8,
故选:C.
10.解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q所以点Q为这条圆弧所在圆的圆心.
故选:C.
二.填空题
11.解:∵OA=OB,AB=BO,
∴OA=OB=AB,即△OAB是等边三角形,
∵BC平分∠ABO,
∴OA=2AC=6,
∴⊙O的周长为2π OA=2π×6=12π.
故答案为12π.
12.解:∵AC是⊙O的直径,
∴∠ABC=90°,
∵∠ACB=∠ADB=45°,
∴△ABC为等腰直角三角形,
∴AC=AB=2,
∴⊙O的半径长.
故答案为.
13.解:作点A关于CD的对称点A′,连接A′B就是最小值(P此时为A′B与CD的交点),
∵|OA|=|OB|=|OA′|=|CD|=3cm且∠AOD=2∠AOB=60°,
∴∠AOB=∠BOD=30°,
∵A关于CD的对称点A′,
∴∠DOA′=∠AOD=60°,
∴∠BOA′=∠BOD+∠DOA′=90°,
∴△BOA′为等腰直角三角形,
∴AP+BP的最小值为:|A′B|==3cm.
故答案为:3cm.
14.解:以BC为直径的半圆的面积是2π,以AC为直径的半圆的面积是π()2=,以AB为直径的面积是×π()2=,△ABC的面积是6,因而阴影部分的面积是2π++6﹣=6.
15.解:坐标轴上到圆心距离为5的点有4个,由勾股定理,四个象限中,到圆心距离为5的点有8个,共12个,如图所示.
16.解:∵弦CD⊥AB于点E,CD=8cm,
∴CE=CD=4(cm)
在Rt△OCE中,OC=5cm,CE=4cm,
∴OE===3(cm),
∴AE=AO+OE=5+3=8(cm).
故答案为:8cm.
17.解:连接OC,
∵BC⊥OA,
∴∠ODC=90°,BD=CD,
∵OD=AD,
∴OD=OA==2,
∴CD===2,
∴BC=2CD=4,
故答案为4.
18.解:延长ED,交⊙O于点C,连接OA,
由题意知CE过点O,且OE⊥AB,
则AD=BD=AB=5(寸),
设圆形木材半径为r,
则OD=r﹣1,OA=r,
∵OA2=OD2+AD2,
∴r2=(r﹣1)2+52,
解得r=13,
所以⊙O的直径为26寸,
故答案为:26寸.
19.解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
20.解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=110°,
∴∠AOE=75°,
∴∠BOE=105°,
∴的度数是105°.
故答案为105°.
三.解答题
21.解:连接AO,
∵CD过圆心,C为AB的中点,
∴CD⊥AB,
∵AB=18,C为AB的中点,
∴AC=BC=9,
设圆的半径为x分米,则OA=OD=x分米,
∵CD=27,
∴OC=27﹣x,
在Rt△OAC中,AC2+OC2=OA2,
∴92+(27﹣x)2=x2,
∴x=15(分米),
答:拱门所在圆的半径是15分米.
22.解:(1)根据题意,图形W为以O为圆心,OA为直径的圆.
如图1,连接OD,
∴OA=OD.
∵点C为OA的中点,CD⊥AB,
∴AD=OD.
∴OA=OD=AD.
∴△OAD 是等边三角形.
∴∠AOD=60°.
∴∠ABD=30°.
(2)如图2,
∵∠ADE=∠ABD,
∴∠ADE=30°.
∵∠ADO=60°.
∴∠ODE=90°.
∴OD⊥DE.
∴DE是⊙O的切线.
∴直线DE与图形W的公共点个数为1.
23.解:∵OB=OC∴∠OCB=∠OBC=40°(2分)
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣40°﹣40°=100°(3分)
∴∠AOC=∠AOB+∠BOC=50°+100°=150°(4分)
又∵OA=OC∴∠OAC==15°(6分)
24.解:∵在△ABC中,∠ACB=90°,∠B=25°
∴∠A=90°﹣∠B=65度.
∵CA=CD
∴∠CDA=∠CAD=65°
∴∠ACD=50°
即弧AD的度数是50度.
25.解:如图2所示,在车轮上取A、B两点,设所在圆的圆心为O,半径为rcm.
作弦AB的垂线OC,D为垂足,则D是AB的中点.其推理依据是:垂直弦的直径平分弦.
经测量:AB=90cm,CD=15cm,则AD=45cm;
用含r的代数式表示OD,OD=(r﹣15)cm.
在Rt△OAD中,由勾股定理可列出关于r的方程:
r2=452+(r﹣15)2,
解得r=75.
通过单位换算,得到车轮直径约为六尺六寸,可验证此车轮为兵车之轮.
故答案为:垂直弦的直径平分弦,45,(r﹣15),452+(r﹣15)2.
26.解:过点O作OD⊥AB于点D,连接OA,
∵在Rt△ODC中,∠OCA=30°,OC=8cm,
∴OD=OC=4cm,
∵在Rt△OAD中,OA=5cm,
∴AD==3,
∴AB=2AD=6.
27.证明:连接ME、MD,
∵BD、CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC,
∴点B、C、D、E在以点M为圆心的同一圆上.
一.选择题
1.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为( )
A. B. C.24 D.16
2.如图,AB是⊙O的直径,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则∠DAC等于( )
A.15° B.30° C.45° D.60°
3.下列语句中不正确的有( )
①相等的圆心角所对的弧相等;
②平分弦的直径垂直于弦;
③圆是轴对称图形,任何一条直径所在直线都是它的对称轴;
④长度相等的两条弧是等弧.
A.3个 B.2个 C.1个 D.以上都不对
4.如图,点A,B,C都在⊙O上,若∠C=34°,则∠AOB为( )
A.34° B.56° C.60° D.68°
5.已知AB是半径为5的圆的一条弦,则AB的长不可能是( )
A.4 B.8 C.10 D.12
6.如图,AB是半圆O的直径,∠BAC=20°,则∠D的度数是( )
A.70° B.100° C.110° D.120°
7.对下列生活现象的解释其数学原理运用错误的是( )
A.把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理
B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理
C.将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理
D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理
8.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是( )
A.12寸 B.24寸 C.13寸 D.26寸
9.P为⊙O内一点,OP=3,⊙O半径为5,则经过P点的最短弦长为( )
A.5 B.6 C.8 D.10
10.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么这条圆弧所在的圆的圆心为图中的( )
A.M B.P C.Q D.R
二.填空题
11.如图,点A、B在⊙O上,且AB=BO.∠ABO的平分线与AO相交于点C,若AC=3,则⊙O的周长为 .(结果保留π)
12.如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,∠ADB=45°,则⊙O的半径长为 .
13.如图,⊙O的直径CD为6cm,OA,OB都是⊙O的半径,∠AOD=2∠AOB=60°,点P在直径CD上移动,则AP+BP的最小值为 .
14.如图,在Rt△ABC中,AC=3,BC=4,分别以它的三边为直径向上作三个半圆,则阴影部分面积为 .(不取近似值)
15.在直角坐标系中,横坐标和纵坐标都是整数的点称为格点.已知一个圆的圆心在原点,半径等于5,那么这个圆上的格点有 个.
16.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE= .
17.如图,点A在⊙O上,弦BC垂直平分OA,垂足为D.若OA=4,则BC的长为 .
18.《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有圆材埋壁中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材埋在墙壁中,不知其大小用锯子去锯这个木材,锯口深1寸(即DE=1寸),锯道长1尺(即弦AB=1尺),问这块圆形木材的直径是多少?”该问题的答案是 (注:1尺=10寸)
19.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 度.
20.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 .
三.解答题
21.如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端AB=18分米,C为AB中点,D为拱门最高点,圆心O在线段CD上,CD=27分米,求拱门所在圆的半径.
22.在平面内,O为线段AB的中点,所有到点O的距离等于OA的点组成图形W.取OA的中点C,过点C作CD⊥AB交图形W于点D,D在直线AB的上方,连接AD,BD.
(1)求∠ABD的度数;
(2)若点E在线段CA的延长线上,且∠ADE=∠ABD,求直线DE与图形W的公共点个数.
23.如图:A、B、C是⊙O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
24.已知:如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,CA长为半径的圆交AB于D,求的度数.
25.如图1是博物馆展出的古代车轮实物,《周礼 考工记》记载:“…故兵车之轮六尺有六寸,田车之轮六尺有三寸…”据此,我们可以通过计算车轮的半径来验证车轮类型,请将以下推理过程补充完整.
如图2所示,在车轮上取A、B两点,设所在圆的圆心为O,半径为rcm.
作弦AB的垂线OC,D为垂足,则D是AB的中点.其推理依据是: .
经测量:AB=90cm,CD=15cm,则AD= cm;
用含r的代数式表示OD,OD= cm.
在Rt△OAD中,由勾股定理可列出关于r的方程:
r2= ,
解得r=75.
通过单位换算,得到车轮直径约为六尺六寸,可验证此车轮为兵车之轮.
26.如图,⊙O的半径OB=5cm,AB是⊙O的弦,点C是AB延长线上一点,且∠OCA=30°,OC=8cm,求AB的长.
27.已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
参考答案与试题解析
一.选择题
1.解:如图,过点O作OC⊥AB,垂足为C,
∵∠AOB=90°,∠A=∠AOC=45°,
∴OC=AC,
∵CO=4,
∴AC=4,
∴OA=4,
∴⊙O的直径长为8.
故选:B.
2.解:∵OA=OC,
∴∠CAO=∠ACO,
∵AD∥OC,
∴∠DAC=∠ACO,
∴∠DAC=∠CAB,
∵∠DAB=60°,
∴∠DAC=∠DAB=30°,
故选:B.
3.解:在同圆或等圆中,相等的圆心角所对的弧相等,所以①的说法错误;
平分弦(非直径)的直径垂直于弦,所以②的说法错误;
圆是轴对称图形,任何一条直径所在直线都是它的对称轴,所以③的说法正确;
能完全重合的两条弧是等弧,所以④的说法错误.
故选:A.
4.解:∵∠C=34°,
∴∠AOB=2∠C=68°.
故选:D.
5.解:因为圆中最长的弦为直径,所以弦长L≤10.
故选:D.
6.解:连接BC,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°,
∵∠BAC=20°,
∴∠ABC=90°﹣20°=70°,
∵圆内接四边形的对角互补,
∴∠D+∠ABC=180°,
∴∠D=180°﹣70°=110°,
故选:C.
7.解:A、把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理,正确;
B、木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“两点确定一条直线”的原理,故错误;
C、将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理,正确;
D、将车轮设计为圆形是运用了“圆的旋转对称性”的原理,正确,
故选:B.
8.解:连接OA,
∵AB⊥CD,且AB=10寸,
∴AE=BE=5寸,
设圆O的半径OA的长为x,则OC=OD=x,
∵CE=1,
∴OE=x﹣1,
在直角三角形AOE中,根据勾股定理得:
x2﹣(x﹣1)2=52,化简得:x2﹣x2+2x﹣1=25,
即2x=26,
∴CD=26(寸).
故选:D.
9.解:
如图,过P作AB⊥OP,交⊙O于A、B,则线段AB是过P点的最短的弦,连接OA,
则∠OPA=90°,
由勾股定理得:AP===4,
∵OP⊥AB,OP过圆心O,
∴BP=AP=4,
即AB=4+4=8,
故选:C.
10.解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q所以点Q为这条圆弧所在圆的圆心.
故选:C.
二.填空题
11.解:∵OA=OB,AB=BO,
∴OA=OB=AB,即△OAB是等边三角形,
∵BC平分∠ABO,
∴OA=2AC=6,
∴⊙O的周长为2π OA=2π×6=12π.
故答案为12π.
12.解:∵AC是⊙O的直径,
∴∠ABC=90°,
∵∠ACB=∠ADB=45°,
∴△ABC为等腰直角三角形,
∴AC=AB=2,
∴⊙O的半径长.
故答案为.
13.解:作点A关于CD的对称点A′,连接A′B就是最小值(P此时为A′B与CD的交点),
∵|OA|=|OB|=|OA′|=|CD|=3cm且∠AOD=2∠AOB=60°,
∴∠AOB=∠BOD=30°,
∵A关于CD的对称点A′,
∴∠DOA′=∠AOD=60°,
∴∠BOA′=∠BOD+∠DOA′=90°,
∴△BOA′为等腰直角三角形,
∴AP+BP的最小值为:|A′B|==3cm.
故答案为:3cm.
14.解:以BC为直径的半圆的面积是2π,以AC为直径的半圆的面积是π()2=,以AB为直径的面积是×π()2=,△ABC的面积是6,因而阴影部分的面积是2π++6﹣=6.
15.解:坐标轴上到圆心距离为5的点有4个,由勾股定理,四个象限中,到圆心距离为5的点有8个,共12个,如图所示.
16.解:∵弦CD⊥AB于点E,CD=8cm,
∴CE=CD=4(cm)
在Rt△OCE中,OC=5cm,CE=4cm,
∴OE===3(cm),
∴AE=AO+OE=5+3=8(cm).
故答案为:8cm.
17.解:连接OC,
∵BC⊥OA,
∴∠ODC=90°,BD=CD,
∵OD=AD,
∴OD=OA==2,
∴CD===2,
∴BC=2CD=4,
故答案为4.
18.解:延长ED,交⊙O于点C,连接OA,
由题意知CE过点O,且OE⊥AB,
则AD=BD=AB=5(寸),
设圆形木材半径为r,
则OD=r﹣1,OA=r,
∵OA2=OD2+AD2,
∴r2=(r﹣1)2+52,
解得r=13,
所以⊙O的直径为26寸,
故答案为:26寸.
19.解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
20.解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=110°,
∴∠AOE=75°,
∴∠BOE=105°,
∴的度数是105°.
故答案为105°.
三.解答题
21.解:连接AO,
∵CD过圆心,C为AB的中点,
∴CD⊥AB,
∵AB=18,C为AB的中点,
∴AC=BC=9,
设圆的半径为x分米,则OA=OD=x分米,
∵CD=27,
∴OC=27﹣x,
在Rt△OAC中,AC2+OC2=OA2,
∴92+(27﹣x)2=x2,
∴x=15(分米),
答:拱门所在圆的半径是15分米.
22.解:(1)根据题意,图形W为以O为圆心,OA为直径的圆.
如图1,连接OD,
∴OA=OD.
∵点C为OA的中点,CD⊥AB,
∴AD=OD.
∴OA=OD=AD.
∴△OAD 是等边三角形.
∴∠AOD=60°.
∴∠ABD=30°.
(2)如图2,
∵∠ADE=∠ABD,
∴∠ADE=30°.
∵∠ADO=60°.
∴∠ODE=90°.
∴OD⊥DE.
∴DE是⊙O的切线.
∴直线DE与图形W的公共点个数为1.
23.解:∵OB=OC∴∠OCB=∠OBC=40°(2分)
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣40°﹣40°=100°(3分)
∴∠AOC=∠AOB+∠BOC=50°+100°=150°(4分)
又∵OA=OC∴∠OAC==15°(6分)
24.解:∵在△ABC中,∠ACB=90°,∠B=25°
∴∠A=90°﹣∠B=65度.
∵CA=CD
∴∠CDA=∠CAD=65°
∴∠ACD=50°
即弧AD的度数是50度.
25.解:如图2所示,在车轮上取A、B两点,设所在圆的圆心为O,半径为rcm.
作弦AB的垂线OC,D为垂足,则D是AB的中点.其推理依据是:垂直弦的直径平分弦.
经测量:AB=90cm,CD=15cm,则AD=45cm;
用含r的代数式表示OD,OD=(r﹣15)cm.
在Rt△OAD中,由勾股定理可列出关于r的方程:
r2=452+(r﹣15)2,
解得r=75.
通过单位换算,得到车轮直径约为六尺六寸,可验证此车轮为兵车之轮.
故答案为:垂直弦的直径平分弦,45,(r﹣15),452+(r﹣15)2.
26.解:过点O作OD⊥AB于点D,连接OA,
∵在Rt△ODC中,∠OCA=30°,OC=8cm,
∴OD=OC=4cm,
∵在Rt△OAD中,OA=5cm,
∴AD==3,
∴AB=2AD=6.
27.证明:连接ME、MD,
∵BD、CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC,
∴点B、C、D、E在以点M为圆心的同一圆上.
