2021-2022学年鲁教版六年级数学下册6.7完全平方公式 自主提升训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版六年级数学下册6.7完全平方公式 自主提升训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 71.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版六年级数学下册《6-7完全平方公式》自主提升训练(附答案)
1.若x2+2(m﹣3)x+16是完全平方式,则m的值等于 .
2.若实数x、y满足x﹣2=y,则代数式x2﹣2xy+y2的值为 .
3.关于x的二次多项式x2+6x+m是一个完全平方式,则常数项m= .
4.若a2+b2=7,a﹣b=3,则ab的值为 .
5.若a2+b2=6,a+b=3,则ab的值为 .
6.计算:(x+2)2﹣(x﹣2)(x+2)= .
7.是一个完全平方式,则k= .
8.知a+b=5,ab=3,则a2+b2﹣3ab= .
9.若a+b=1,则a2﹣b2+2b的值为 .
10.已知a2+b2﹣6a+13=4b,则2a+b的值是
11.对于代数式4x2﹣12x+11,利用完全平方公式,可求其最小值是 .
12.已知x+y=5,xy=﹣24,则x2+y2= .
13.若(x+y)2=36,xy=5,则x2+y2= .
14.若(2a+b)2=11,ab=1,则(2a﹣b)2的值是 .
15.已知x﹣y=6,xy=﹣8,则(x+y)2的值为 .
16.已知4m+n=90,2m﹣3n=10,求(m+2n)2﹣(3m﹣n)2= .
17.若x+y=5,xy=6,则x2+y2+2027的值是 .
18.若x+y=5,则(x﹣y)2+4xy+1的值为 .
19.已知a﹣b=4,则a2﹣b2﹣8b的值为 .
20.若a+b=3,a﹣b=7,则ab= .
21.已知(x+y)2=18,(x﹣y)2=6,分别求下列代数式的值:
(1)x2+y2;
(2)x2+3xy+y2;
(3)x4+y4.
22.已知a+b=3,ab=﹣12,求下列各式的值.
(1)a2﹣ab+b2
(2)(a﹣b)2.
23.已知x2﹣5x+1=0,求x4+.
24.已知m满足(3m﹣2023)2+(2022﹣3m)2=5.
(1)求(2023﹣3m)(2022﹣3m)的值;
(2)求6m﹣4045的值.
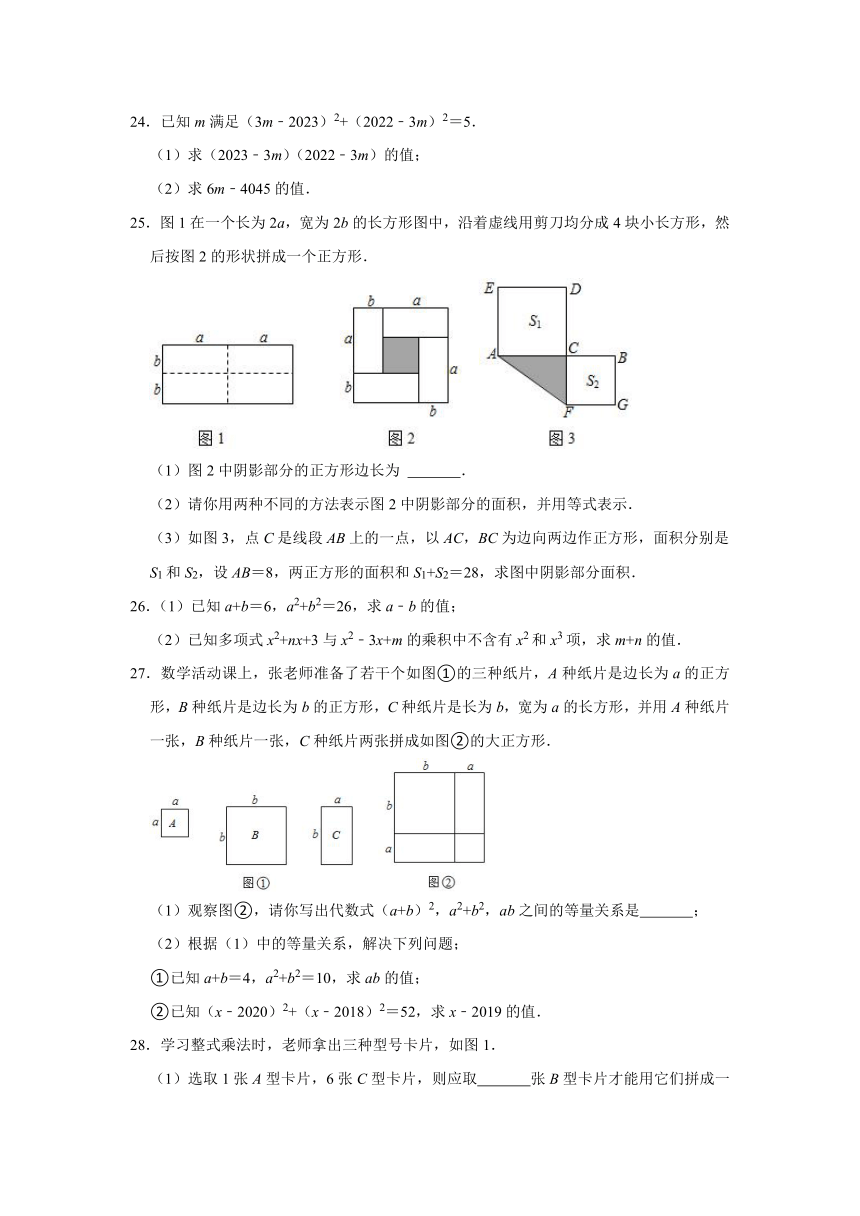
25.图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的正方形边长为 .
(2)请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.
(3)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,面积分别是S1和S2,设AB=8,两正方形的面积和S1+S2=28,求图中阴影部分面积.
26.(1)已知a+b=6,a2+b2=26,求a﹣b的值;
(2)已知多项式x2+nx+3与x2﹣3x+m的乘积中不含有x2和x3项,求m+n的值.
27.数学活动课上,张老师准备了若干个如图①的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图②的大正方形.
(1)观察图②,请你写出代数式(a+b)2,a2+b2,ab之间的等量关系是 ;
(2)根据(1)中的等量关系,解决下列问题;
①已知a+b=4,a2+b2=10,求ab的值;
②已知(x﹣2020)2+(x﹣2018)2=52,求x﹣2019的值.
28.学习整式乘法时,老师拿出三种型号卡片,如图1.
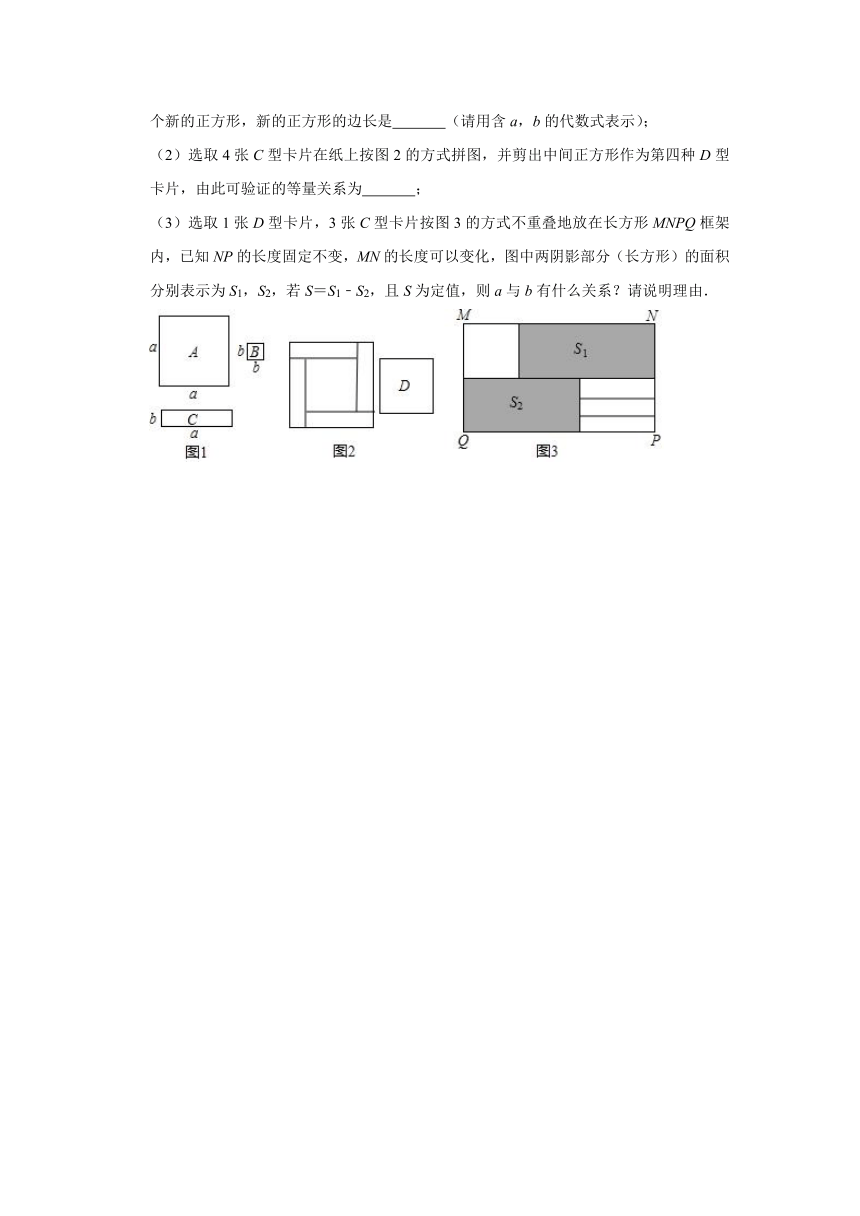
(1)选取1张A型卡片,6张C型卡片,则应取 张B型卡片才能用它们拼成一个新的正方形,新的正方形的边长是 (请用含a,b的代数式表示);
(2)选取4张C型卡片在纸上按图2的方式拼图,并剪出中间正方形作为第四种D型卡片,由此可验证的等量关系为 ;
(3)选取1张D型卡片,3张C型卡片按图3的方式不重叠地放在长方形MNPQ框架内,已知NP的长度固定不变,MN的长度可以变化,图中两阴影部分(长方形)的面积分别表示为S1,S2,若S=S1﹣S2,且S为定值,则a与b有什么关系?请说明理由.
参考答案
1.解:∵x2+2(m﹣3)x+16是完全平方式,
∴2(m﹣3)x=±2 x 4,
解得:m=7或﹣1,
故答案为:7或﹣1.
2.解:由x﹣2=y可得x﹣y=2,
∴x2﹣2xy+y2
=(x﹣y)2
=22
=4.
故答案为:4.
3.解:∵6x=2×3 x,
∴m=32=9.
故答案为:9.
4.解:∵a﹣b=3,
∴(a﹣b)2=9,即a2+b2﹣2ab=9,
∵a2+b2=7,
∴7﹣2ab=9,
∴ab=﹣1,
故答案为:﹣1.
5.解:由a+b=3两边平方,得
a2+2ab+b2=9 ①,
a2+b2=6 ②,
①﹣②,得2ab=3,
两边都除以2,得
ab=.
故答案为:.
6.解:(x+2)2﹣(x﹣2)(x+2)
=x2+4x+4﹣x2+4
=4x+8.
故答案为:4x+8.
7.解:∵x2﹣kx+=x2﹣kx+()2,
∴﹣kx=±2×x×,
解得k=±.
故答案为:±.
8.解:∵a+b=5,ab=3,
∴a2+b2﹣3ab=(a+b)2﹣5ab
=25﹣15
=10,
故答案为:10.
9.解:∵a+b=1,
∴a2﹣b2+2b=(a+b)(a﹣b)+2b
=1×(a﹣b)+2b
=a﹣b+2b
=a+b
=1,
故答案为:1.
10.解:a2+b2﹣6a+13=4b,
(a2﹣6a+9)+(b2﹣4b+4)=0,
(a﹣3)2+(b﹣2)2=0,
∴a﹣3=0,b﹣2=0,
解得a=3,b=2,
∴2a+b=6+2=8.
故答案为:8.
11.解:4x2﹣12x+11
=4(x2﹣3x)+11
=4(x2﹣3x+﹣)+11
=4(x﹣)2+2,
则代数式4x2﹣12x+11的最小值是2.
故答案为:2.
12.解:∵x+y=5,xy=﹣24,
∴x2+y2=(x+y)2﹣2xy
=52﹣2×(﹣24)
=73.
故答案为73.
13.解:∵(x+y)2=36,xy=5,
∴x2+y2=(x+y)2﹣2xy=36﹣2×5=26.
故答案为:26.
14.解:∵(2a+b)2=4a2+4ab+b2=11,ab=1,
∴4a2+b2=7,
∴(2a﹣b)2=4a2﹣4ab+b2=7﹣4=3.
故答案为:3.
15.解:∵x﹣y=﹣6,
∴(x﹣y)2=x2+y2﹣2xy=36,
∵xy=﹣8,
∴x2+y2﹣2×(﹣8)=36,
∴x2+y2=20,
∵(x+y)2=x2+y2+2xy=20﹣16=4.
故答案是:4.
16.解:∵4m+n=90,2m﹣3n=10,
∴原式=(m+2n+3m﹣n)(m+2n﹣3m+n)
=(4m+n)(﹣2m+3n)
=﹣(4m+n)(2m﹣3n)
=﹣90×10
=﹣900.
故答案为:﹣900.
17.解:∵x+y=5,xy=6,
∴x2+y2+2027=(x+y)2﹣2xy+2027
=52﹣2×6+2027
=2040.
故答案为2040.
18.解:原式=x2﹣2xy+y2+4xy+1
=x2+2xy+y2+1
=(x+y)2+1
当x+y=5时,原式=52+1=26.
故答案为26.
19.解:∵a﹣b=4,
∴a=b+4,
∴a2=(b+4)2=b2+8b+16,
∴a2﹣b2﹣8b=b2+8b+16﹣b2﹣8b=16.
故答案为16.
20.解:∵a+b=3,a﹣b=7,
∴
∴2a=10,
解得:a=5,
把a=5代入a+b=3得:b=﹣2,
∴ab=5×(﹣2)=﹣10,
故答案为:﹣10.
21.解:(1)∵(x+y)2=18,(x﹣y)2=6
∴x2+y2+2xy=18,x2+y2﹣2xy=6,
∴x2+y2=12,xy=3,
则原式=12;
(2)原式=12+3×3=21;
(3)原式=(x2+y2)2﹣2x2y2
=122﹣2×32
=126.
22.解:(1)将a+b=3两边平方得:(a+b)2=9,即a2+2ab+b2=9,
∵ab=﹣12,
∴a2﹣24+b2=9,即a2+b2=33,
则a2﹣ab+b2=33+12=45;
(2)∵a2+b2=33,ab=﹣12,
∴(a﹣b)2=a2﹣2ab+b2=33+24=57.
23.解:方程x2﹣5x+1=0两边同时除以x解得:x﹣5+=0,
则x+=5,
两边平方得:x2+2+=25,则x2+=23,
两边再平方得:x4++2=529,
则x4+=527.
24.解:(1)设A=3m﹣2023,B=2022﹣3m,可得A+B=﹣1,
∵A2+B2=5,
∴(2023﹣3m)(2022﹣3m)=﹣AB=﹣[(A+B)2﹣(A2+B2)]=2;
(2)∵(6m﹣4045)2=(A﹣B)2=(A+B)2﹣4AB=1+8=9,
∴6m﹣4045=±3.
25.解:(1)由大、小正方形的边长与长方形边长之间的关系可得,
阴影部分是边长为(a﹣b)的正方形,
故答案为:a﹣b;
(2)方法一:阴影部分是边长为(a﹣b)的正方形,因此面积为(a﹣b)2,
方法2:从边长为(a+b)的正方形面积减去4个长为a,宽为b长方形的面积可得,
(a+b)2﹣4ab,
于是有:(a﹣b)2=(a+b)2﹣4ab;
(3)设大正方形的边长为a、小正方形的边长b,
则a+b=8,a2+b2=28,
由(a+b)2=a2+b2+2ab得,
82=28+2ab,
即ab=18,
因此阴影部分的面积为ab=9,
答:阴影部分的面积为9.
26.解:(1)∵a+b=6,
∴(a+b)2=36.
∴a2+b2+2ab=36.
又∵a2+b2=26,
∴26+2ab=36.
∴ab=5.
∴(a﹣b)2=a2+b2﹣2ab=26﹣10=16.
∴a﹣b=±4.
(2)(x2+nx+3)(x2﹣3x+m)
=x4﹣3x3+mx2+nx3﹣3nx2+mnx+3x2﹣9x+3m
=x4+(n﹣3)x3+(m﹣3n+3)x2+(mn﹣9)x+3m.
∵多项式x2+nx+3与x2﹣3x+m的乘积中不含有x2和x3项,
∴n﹣3=0,m﹣3n+3=0.
∴m=6,n=3.
∴m+n=6+3=9.
27.解:(1)(a+b)2=a2+b2+2ab;
∵图②是边长为(a+b)的正方形,
∴S=(a+b)2
∵图②可看成1个边长为a的正方形,1个边长为b的正方形以及2个长为b,宽为a的长方形的组合图形,
∴S=a2+b2+2ab,
∴(a+b)2=a2+b2+2ab;
故答案为:(a+b)2=a2+b2+2ab.
(2)①∵a+b=4,
∴(a+b)2=16,
即a2+b2+2ab=16.
又∵a2+b2=10,
∴ab=3;
②设x﹣2019=a,
则x﹣2020=a﹣1,
x﹣2018=a+1,
∵(x﹣2020)2+(x﹣2018)2=52,
∴(a﹣1)2+(a+1)2=52,
∴a2﹣2a+1+a2+2a+1=52,
解得a2=25,
即(x﹣2019)2=25,
∴x﹣2019=±5.
28.解:(1)A型卡片的面积为a2,B型卡片的面积为b2,C型卡片的面积为ab,
题中已经选择1张A型卡片,6张C型卡片,面积之和为a2+6ab,
由完全平方公式的几何背景可知一个正方形的面积可以表达成一个完全平方公式,可以很轻易得知a2+6ab+9b2=(a+3b)2,
故应取9张B型卡片才能用它们拼成一个新的正方形,新的正方形的边长是a+3b
故答案为:9;a+3b
(2)选取4张C型卡片在纸上按图2的方式拼图,可以得到一个边长为(a+b)的正方形,
剪出中间正方形作为第四种D型卡片,可知D型卡片的面积为一个边长为(a+b)的正方形的面积减去4张C型卡片的面积,即:(a+b)2﹣4ab,
由图可得D型卡片是一个边长为(a﹣b)的正方形,
由正方形的面积为边长的平方可知:(a﹣b)2=(a+b)2﹣4ab
故答案为:(a﹣b)2=(a+b)2﹣4ab
(3)设MN长为x
S1=(a﹣b)[x﹣(a﹣b)]=ax﹣bx﹣a2+2ab﹣b2
S2=3b(x﹣a)=3bx﹣3ab
S=S1﹣S2=(a﹣4b)x﹣a2+5ab﹣b2
由题意得,若S为定值,则S将不随x的变化而变化,
可知当a﹣4b=0时,即a=4b时,S=﹣a2+5ab﹣b2为定值
故答案为:a=4b时,S为定值
1.若x2+2(m﹣3)x+16是完全平方式,则m的值等于 .
2.若实数x、y满足x﹣2=y,则代数式x2﹣2xy+y2的值为 .
3.关于x的二次多项式x2+6x+m是一个完全平方式,则常数项m= .
4.若a2+b2=7,a﹣b=3,则ab的值为 .
5.若a2+b2=6,a+b=3,则ab的值为 .
6.计算:(x+2)2﹣(x﹣2)(x+2)= .
7.是一个完全平方式,则k= .
8.知a+b=5,ab=3,则a2+b2﹣3ab= .
9.若a+b=1,则a2﹣b2+2b的值为 .
10.已知a2+b2﹣6a+13=4b,则2a+b的值是
11.对于代数式4x2﹣12x+11,利用完全平方公式,可求其最小值是 .
12.已知x+y=5,xy=﹣24,则x2+y2= .
13.若(x+y)2=36,xy=5,则x2+y2= .
14.若(2a+b)2=11,ab=1,则(2a﹣b)2的值是 .
15.已知x﹣y=6,xy=﹣8,则(x+y)2的值为 .
16.已知4m+n=90,2m﹣3n=10,求(m+2n)2﹣(3m﹣n)2= .
17.若x+y=5,xy=6,则x2+y2+2027的值是 .
18.若x+y=5,则(x﹣y)2+4xy+1的值为 .
19.已知a﹣b=4,则a2﹣b2﹣8b的值为 .
20.若a+b=3,a﹣b=7,则ab= .
21.已知(x+y)2=18,(x﹣y)2=6,分别求下列代数式的值:
(1)x2+y2;
(2)x2+3xy+y2;
(3)x4+y4.
22.已知a+b=3,ab=﹣12,求下列各式的值.
(1)a2﹣ab+b2
(2)(a﹣b)2.
23.已知x2﹣5x+1=0,求x4+.
24.已知m满足(3m﹣2023)2+(2022﹣3m)2=5.
(1)求(2023﹣3m)(2022﹣3m)的值;
(2)求6m﹣4045的值.
25.图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的正方形边长为 .
(2)请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.
(3)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,面积分别是S1和S2,设AB=8,两正方形的面积和S1+S2=28,求图中阴影部分面积.
26.(1)已知a+b=6,a2+b2=26,求a﹣b的值;
(2)已知多项式x2+nx+3与x2﹣3x+m的乘积中不含有x2和x3项,求m+n的值.
27.数学活动课上,张老师准备了若干个如图①的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图②的大正方形.
(1)观察图②,请你写出代数式(a+b)2,a2+b2,ab之间的等量关系是 ;
(2)根据(1)中的等量关系,解决下列问题;
①已知a+b=4,a2+b2=10,求ab的值;
②已知(x﹣2020)2+(x﹣2018)2=52,求x﹣2019的值.
28.学习整式乘法时,老师拿出三种型号卡片,如图1.
(1)选取1张A型卡片,6张C型卡片,则应取 张B型卡片才能用它们拼成一个新的正方形,新的正方形的边长是 (请用含a,b的代数式表示);
(2)选取4张C型卡片在纸上按图2的方式拼图,并剪出中间正方形作为第四种D型卡片,由此可验证的等量关系为 ;
(3)选取1张D型卡片,3张C型卡片按图3的方式不重叠地放在长方形MNPQ框架内,已知NP的长度固定不变,MN的长度可以变化,图中两阴影部分(长方形)的面积分别表示为S1,S2,若S=S1﹣S2,且S为定值,则a与b有什么关系?请说明理由.
参考答案
1.解:∵x2+2(m﹣3)x+16是完全平方式,
∴2(m﹣3)x=±2 x 4,
解得:m=7或﹣1,
故答案为:7或﹣1.
2.解:由x﹣2=y可得x﹣y=2,
∴x2﹣2xy+y2
=(x﹣y)2
=22
=4.
故答案为:4.
3.解:∵6x=2×3 x,
∴m=32=9.
故答案为:9.
4.解:∵a﹣b=3,
∴(a﹣b)2=9,即a2+b2﹣2ab=9,
∵a2+b2=7,
∴7﹣2ab=9,
∴ab=﹣1,
故答案为:﹣1.
5.解:由a+b=3两边平方,得
a2+2ab+b2=9 ①,
a2+b2=6 ②,
①﹣②,得2ab=3,
两边都除以2,得
ab=.
故答案为:.
6.解:(x+2)2﹣(x﹣2)(x+2)
=x2+4x+4﹣x2+4
=4x+8.
故答案为:4x+8.
7.解:∵x2﹣kx+=x2﹣kx+()2,
∴﹣kx=±2×x×,
解得k=±.
故答案为:±.
8.解:∵a+b=5,ab=3,
∴a2+b2﹣3ab=(a+b)2﹣5ab
=25﹣15
=10,
故答案为:10.
9.解:∵a+b=1,
∴a2﹣b2+2b=(a+b)(a﹣b)+2b
=1×(a﹣b)+2b
=a﹣b+2b
=a+b
=1,
故答案为:1.
10.解:a2+b2﹣6a+13=4b,
(a2﹣6a+9)+(b2﹣4b+4)=0,
(a﹣3)2+(b﹣2)2=0,
∴a﹣3=0,b﹣2=0,
解得a=3,b=2,
∴2a+b=6+2=8.
故答案为:8.
11.解:4x2﹣12x+11
=4(x2﹣3x)+11
=4(x2﹣3x+﹣)+11
=4(x﹣)2+2,
则代数式4x2﹣12x+11的最小值是2.
故答案为:2.
12.解:∵x+y=5,xy=﹣24,
∴x2+y2=(x+y)2﹣2xy
=52﹣2×(﹣24)
=73.
故答案为73.
13.解:∵(x+y)2=36,xy=5,
∴x2+y2=(x+y)2﹣2xy=36﹣2×5=26.
故答案为:26.
14.解:∵(2a+b)2=4a2+4ab+b2=11,ab=1,
∴4a2+b2=7,
∴(2a﹣b)2=4a2﹣4ab+b2=7﹣4=3.
故答案为:3.
15.解:∵x﹣y=﹣6,
∴(x﹣y)2=x2+y2﹣2xy=36,
∵xy=﹣8,
∴x2+y2﹣2×(﹣8)=36,
∴x2+y2=20,
∵(x+y)2=x2+y2+2xy=20﹣16=4.
故答案是:4.
16.解:∵4m+n=90,2m﹣3n=10,
∴原式=(m+2n+3m﹣n)(m+2n﹣3m+n)
=(4m+n)(﹣2m+3n)
=﹣(4m+n)(2m﹣3n)
=﹣90×10
=﹣900.
故答案为:﹣900.
17.解:∵x+y=5,xy=6,
∴x2+y2+2027=(x+y)2﹣2xy+2027
=52﹣2×6+2027
=2040.
故答案为2040.
18.解:原式=x2﹣2xy+y2+4xy+1
=x2+2xy+y2+1
=(x+y)2+1
当x+y=5时,原式=52+1=26.
故答案为26.
19.解:∵a﹣b=4,
∴a=b+4,
∴a2=(b+4)2=b2+8b+16,
∴a2﹣b2﹣8b=b2+8b+16﹣b2﹣8b=16.
故答案为16.
20.解:∵a+b=3,a﹣b=7,
∴
∴2a=10,
解得:a=5,
把a=5代入a+b=3得:b=﹣2,
∴ab=5×(﹣2)=﹣10,
故答案为:﹣10.
21.解:(1)∵(x+y)2=18,(x﹣y)2=6
∴x2+y2+2xy=18,x2+y2﹣2xy=6,
∴x2+y2=12,xy=3,
则原式=12;
(2)原式=12+3×3=21;
(3)原式=(x2+y2)2﹣2x2y2
=122﹣2×32
=126.
22.解:(1)将a+b=3两边平方得:(a+b)2=9,即a2+2ab+b2=9,
∵ab=﹣12,
∴a2﹣24+b2=9,即a2+b2=33,
则a2﹣ab+b2=33+12=45;
(2)∵a2+b2=33,ab=﹣12,
∴(a﹣b)2=a2﹣2ab+b2=33+24=57.
23.解:方程x2﹣5x+1=0两边同时除以x解得:x﹣5+=0,
则x+=5,
两边平方得:x2+2+=25,则x2+=23,
两边再平方得:x4++2=529,
则x4+=527.
24.解:(1)设A=3m﹣2023,B=2022﹣3m,可得A+B=﹣1,
∵A2+B2=5,
∴(2023﹣3m)(2022﹣3m)=﹣AB=﹣[(A+B)2﹣(A2+B2)]=2;
(2)∵(6m﹣4045)2=(A﹣B)2=(A+B)2﹣4AB=1+8=9,
∴6m﹣4045=±3.
25.解:(1)由大、小正方形的边长与长方形边长之间的关系可得,
阴影部分是边长为(a﹣b)的正方形,
故答案为:a﹣b;
(2)方法一:阴影部分是边长为(a﹣b)的正方形,因此面积为(a﹣b)2,
方法2:从边长为(a+b)的正方形面积减去4个长为a,宽为b长方形的面积可得,
(a+b)2﹣4ab,
于是有:(a﹣b)2=(a+b)2﹣4ab;
(3)设大正方形的边长为a、小正方形的边长b,
则a+b=8,a2+b2=28,
由(a+b)2=a2+b2+2ab得,
82=28+2ab,
即ab=18,
因此阴影部分的面积为ab=9,
答:阴影部分的面积为9.
26.解:(1)∵a+b=6,
∴(a+b)2=36.
∴a2+b2+2ab=36.
又∵a2+b2=26,
∴26+2ab=36.
∴ab=5.
∴(a﹣b)2=a2+b2﹣2ab=26﹣10=16.
∴a﹣b=±4.
(2)(x2+nx+3)(x2﹣3x+m)
=x4﹣3x3+mx2+nx3﹣3nx2+mnx+3x2﹣9x+3m
=x4+(n﹣3)x3+(m﹣3n+3)x2+(mn﹣9)x+3m.
∵多项式x2+nx+3与x2﹣3x+m的乘积中不含有x2和x3项,
∴n﹣3=0,m﹣3n+3=0.
∴m=6,n=3.
∴m+n=6+3=9.
27.解:(1)(a+b)2=a2+b2+2ab;
∵图②是边长为(a+b)的正方形,
∴S=(a+b)2
∵图②可看成1个边长为a的正方形,1个边长为b的正方形以及2个长为b,宽为a的长方形的组合图形,
∴S=a2+b2+2ab,
∴(a+b)2=a2+b2+2ab;
故答案为:(a+b)2=a2+b2+2ab.
(2)①∵a+b=4,
∴(a+b)2=16,
即a2+b2+2ab=16.
又∵a2+b2=10,
∴ab=3;
②设x﹣2019=a,
则x﹣2020=a﹣1,
x﹣2018=a+1,
∵(x﹣2020)2+(x﹣2018)2=52,
∴(a﹣1)2+(a+1)2=52,
∴a2﹣2a+1+a2+2a+1=52,
解得a2=25,
即(x﹣2019)2=25,
∴x﹣2019=±5.
28.解:(1)A型卡片的面积为a2,B型卡片的面积为b2,C型卡片的面积为ab,
题中已经选择1张A型卡片,6张C型卡片,面积之和为a2+6ab,
由完全平方公式的几何背景可知一个正方形的面积可以表达成一个完全平方公式,可以很轻易得知a2+6ab+9b2=(a+3b)2,
故应取9张B型卡片才能用它们拼成一个新的正方形,新的正方形的边长是a+3b
故答案为:9;a+3b
(2)选取4张C型卡片在纸上按图2的方式拼图,可以得到一个边长为(a+b)的正方形,
剪出中间正方形作为第四种D型卡片,可知D型卡片的面积为一个边长为(a+b)的正方形的面积减去4张C型卡片的面积,即:(a+b)2﹣4ab,
由图可得D型卡片是一个边长为(a﹣b)的正方形,
由正方形的面积为边长的平方可知:(a﹣b)2=(a+b)2﹣4ab
故答案为:(a﹣b)2=(a+b)2﹣4ab
(3)设MN长为x
S1=(a﹣b)[x﹣(a﹣b)]=ax﹣bx﹣a2+2ab﹣b2
S2=3b(x﹣a)=3bx﹣3ab
S=S1﹣S2=(a﹣4b)x﹣a2+5ab﹣b2
由题意得,若S为定值,则S将不随x的变化而变化,
可知当a﹣4b=0时,即a=4b时,S=﹣a2+5ab﹣b2为定值
故答案为:a=4b时,S为定值
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
