2021-2022学年北师大版九年级数学下册3.2圆的对称性 课后自主提升训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.2圆的对称性 课后自主提升训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 295.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3-2圆的对称性》课后自主提升训练(附答案)
1.下列图形中,∠AOB为圆心角的是( )
A.B.C.D.
2.下列语句,错误的是( )
A.直径是弦
B.弦的垂直平分线一定经过圆心
C.相等的圆心角所对的弧相等
D.平分弧的半径垂直于弧所对的弦
3.如图,AB是直径,,∠BOC=40°,则∠AOE的度数为( )
A.30° B.40° C.50° D.60°
4.如图,AB,CD是⊙O的直径,=,若∠AOE=32°,则∠COE的度数是( )
A.32° B.60° C.68° D.64°
5.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
A.8 B.10 C.11 D.12
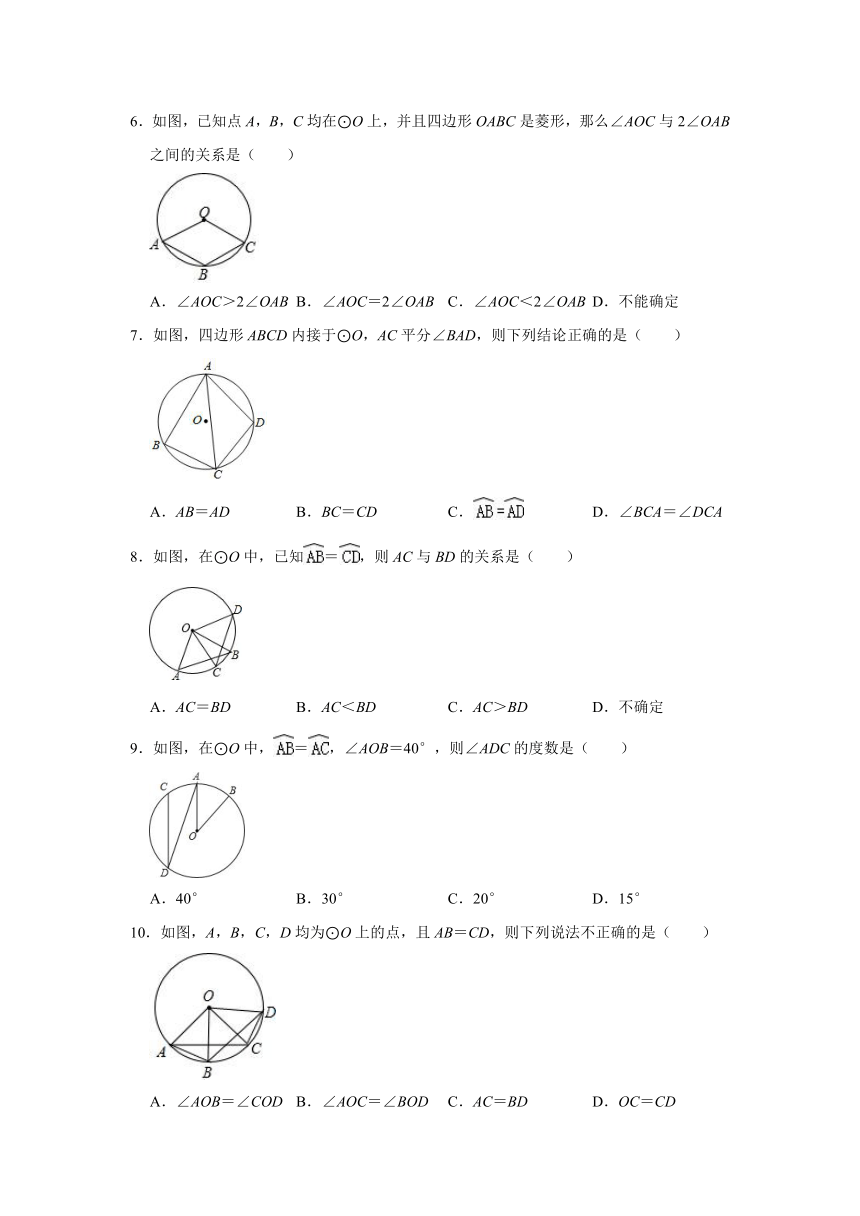
6.如图,已知点A,B,C均在⊙O上,并且四边形OABC是菱形,那么∠AOC与2∠OAB之间的关系是( )
A.∠AOC>2∠OAB B.∠AOC=2∠OAB C.∠AOC<2∠OAB D.不能确定
7.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD C. D.∠BCA=∠DCA
8.如图,在⊙O中,已知=,则AC与BD的关系是( )
A.AC=BD B.AC<BD C.AC>BD D.不确定
9.如图,在⊙O中,=,∠AOB=40°,则∠ADC的度数是( )
A.40° B.30° C.20° D.15°
10.如图,A,B,C,D均为⊙O上的点,且AB=CD,则下列说法不正确的是( )
A.∠AOB=∠COD B.∠AOC=∠BOD C.AC=BD D.OC=CD
11.如图:AB是所对的弦,AB的中垂线CD分别交于C,交AB于D,AD的中垂线EF分别交于E,交AB于F,DB的中垂线GH分别交于G,交AB于H,下列结论中不正确的是( )
A.= B.= C.= D.EF=GH
12.如图所示,在⊙O中,,∠A=30°,则∠B=( )
A.150° B.75° C.60° D.15°
13.在半径为2cm的⊙O中,弦长为2cm的弦所对的圆心角为( )
A.30° B.60° C.90° D.120°
14.如图,已知:AB是⊙O的直径,C、D是上的三等分点,∠AOE=60°,则∠COE是( )
A.40° B.60° C.80° D.120°
15.在⊙O中,弧AB的度数为60°,则弧AB所对的圆心角的度数为 .
16.AB是⊙O的直径,C,D是上两点,且,,的比为3:2:5(,,弧长之和为),则∠AOC= .
17.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,
则圆柱上M,N两点间的距离是 cm.
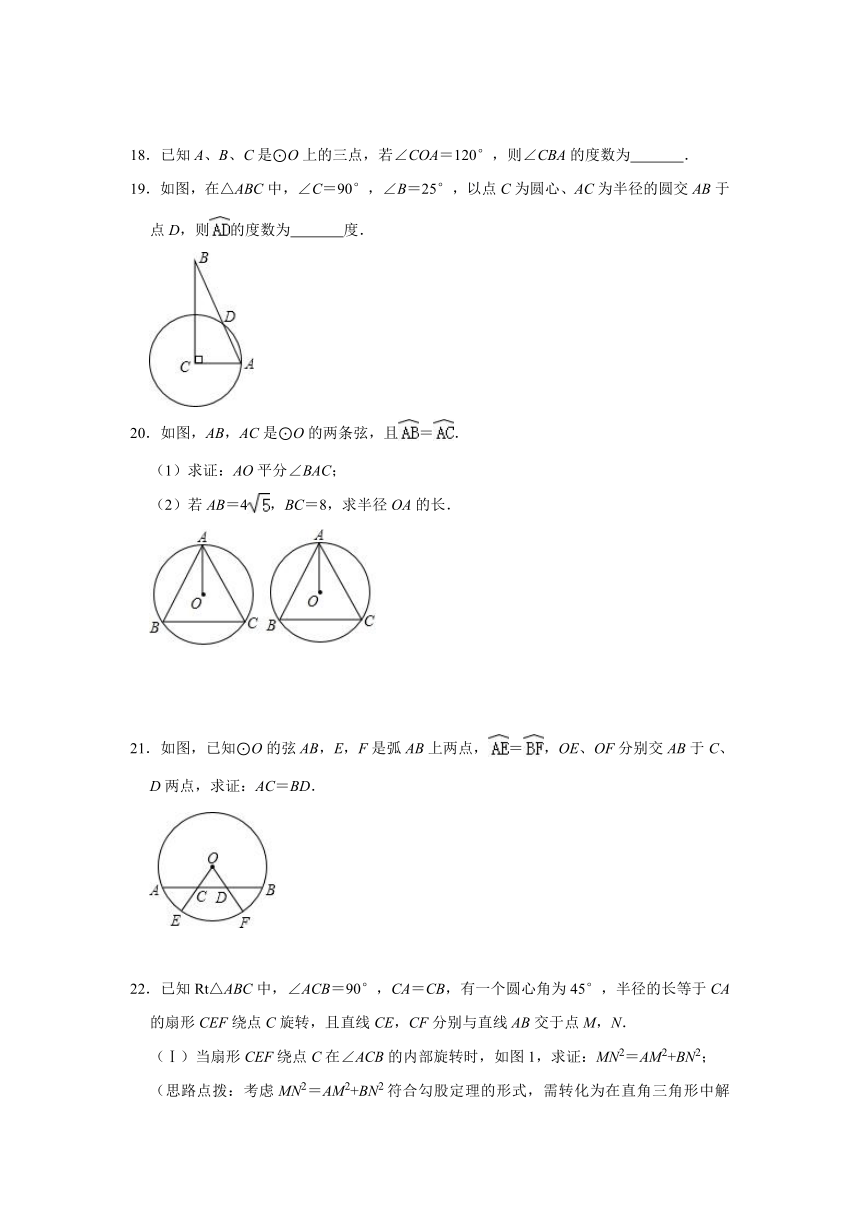
18.已知A、B、C是⊙O上的三点,若∠COA=120°,则∠CBA的度数为 .
19.如图,在△ABC中,∠C=90°,∠B=25°,以点C为圆心、AC为半径的圆交AB于点D,则的度数为 度.
20.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
21.如图,已知⊙O的弦AB,E,F是弧AB上两点,=,OE、OF分别交AB于C、D两点,求证:AC=BD.
22.已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN2=AM2+BN2;
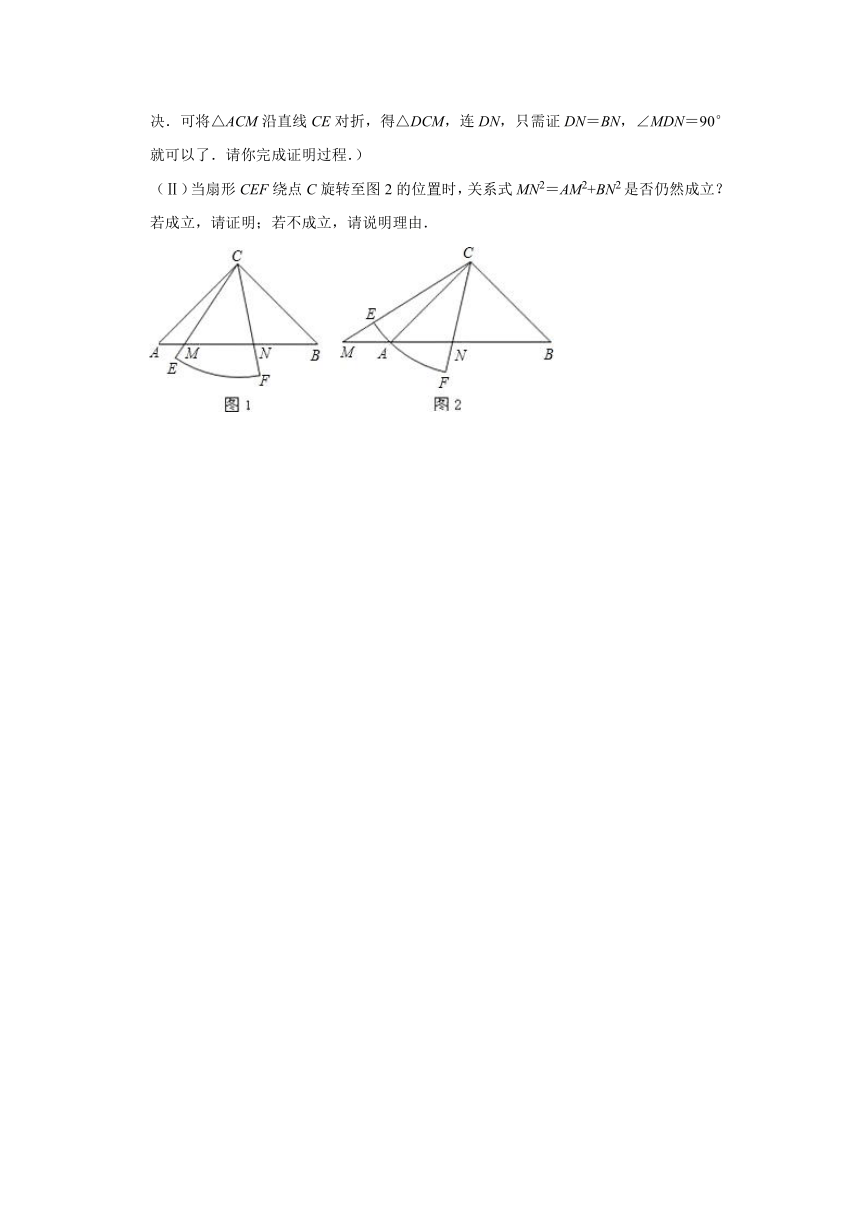
(思路点拨:考虑MN2=AM2+BN2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.
参考答案
1.解:根据圆心角定义可知:
A.顶点不是圆心,所以A选项不符合题意;
B.顶点在圆上,∠AOB圆周角,所以B选项不符合题意;
C.∠AOB顶点是圆心,两边与圆相交,所以C选项符合题意;
D.顶点在圆上,∠AOB圆周角,所以D选项不符合题意.
故选:C.
2.解:A、直径为弦,所以A选项的说法正确;
B、弦的垂直平分线一定经过圆心,所以B选项的说法正确;
C、在同圆或等圆中,相等的圆心角所对的弧相等,所以C选项的说法错误;
D、平分弧的半径垂直于弧所对的弦,所以D选项的说法正确.
故选:C.
3.解:∵,∠BOC=40°,
∴∠BOC=∠COD=∠EOD=40°,
∴∠AOE=180°﹣∠BOE=60°.
故选:D.
4.解:∵=,
∴∠BOD=∠AOE=32°,
∵∠BOD=∠AOC,
∴∠AOC=32°
∴∠COE=32°+32°=64°.
故选:D.
5.解:作直径CF,连接BF,如图,
则∠FBC=90°,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴=,
∴DE=BF=6,
∴BC==8.
解法二:如图,过点A作AM⊥BC于M,AN⊥DE于N.
∵AM⊥BC,AN⊥DE,
∴CM=MB,DN=NE=3,
∵AC=AB=AD=AE,
∴∠BAC=2∠MAC,∠EAD=2∠DAN,
∵∠BAC+∠EAD=180°,
∴2∠CAM+2∠DAN=180°,
∴∠CAM+∠DAN=90°,
∵∠ACM+∠CAM=90°,
∴∠ACM=∠DAN,
∵∠AMC=∠AND=90°,
∴△AMC≌△DNA(AAS),
∴AM=DN=3,
∴CM===4,
∴BC=2CM=8.
故选:A.
6.解:连接OB.
∵四边形OABC是菱形,
∴OA=AB,
又∵OA=OB,
∴△OAB是等边三角形.
同理△OBC是等边三角形.
∴∠A=∠AOB=∠BOC=60°,
∴∠AOC=2∠OAB.
故选:B.
7.解:A、∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;
B、∵AC平分∠BAD,∴∠BAC=∠DAC,∴=,∴BC=CD,故本选项正确;
C、∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;
D、∠BCA与∠DCA的大小关系不确定,故本选项错误.
故选:B.
8.解:∵=,
∴,
∴,
∴AC=BD.
故选:A.
9.解:连接CO,如图:
∵在⊙O中,=,
∴∠AOC=∠AOB,
∵∠AOB=40°,
∴∠AOC=40°,
∴∠ADC=∠AOC=20°,
故选:C.
10.解:∵AB=CD,
∴∠AOB=∠COD,故A正确;
∴∠AOB+∠BOC=∠COD+∠BOC,
∴∠AOC=∠BOD,故B正确;
∴AC=BD,故C正确;
∵△OCD不一定是等边三角形,
∴OC不一定等于CD,故D错误.
故选:D.
11.解:连接EG,AE,
∵AB的中垂线CD分别交于C,
∴=,故A正确;
∵AD的中垂线EF分别交于E,交AB于F,DB的中垂线GH分别交于G,
∴=,故B正确;
∴四边形EFHG是矩形,
∴EF=GH,故D正确.
∵AE>AF=DF,
∴AE>EC,
∴>,故C错误.
故选:C.
12.解:∵在⊙O中,,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B==75°(三角形内角和定理).
故选:B.
13.解:如图,∵OA=OB=AB=2,
∴△OAB是等边三角形,
∴∠AOB=60°.
故选:B.
14.解:∵∠AOE=60°,
∴∠BOE=180°﹣∠AOE=120°,
∴的度数是120°,
∵C、D是上的三等分点,
∴弧CD与弧ED的度数都是40度,
∴∠COE=80°.
故选:C.
15.解:∵弧AB的度数为60°,
∴弧AB所对的圆心角的度数为60°,
故答案为:60°.
16.解:∵,,的比为3:2:5(,,弧长之和为),
∴∠AOC:∠COD:∠BOD=3:2:5,
∴∠AOC=×180°=54°.
故答案为54°.
17.解:根据题意得:EF=AD=BC,MN=2EM=EF,
把该正方形纸片卷成一个圆柱,使点A与点D重合,则线段EF形成一直径为10cm的圆,线段EF为圆上的一段弧.
所对的圆心角为:×360°=120°,
所以圆柱上M,N两点间的距离为:2×5×sin60°=5cm.
故答案为:5.
18.解:如图
当B点在优弧AC上,则∠ABC=∠AOC=60°;
当B点在劣弧AC上,即B′点,则∠B′+∠B=180°,
所以∠B′=120°.
故答案为:60°或120°.
19.解:连接CD,∵∠ACB=90°,∠B=25°,∴∠A=90°﹣∠B=65°,
∵CA=CD,∴∠A=∠CDA=65°,∴∠ACD=180°﹣2∠A=50°,
∴弧AD的度数是50度.
20.证明:(1)连接OB、OC,
∵=.
∴AB=AC,
∵OC=OB,OA=OA,
在△AOB与△AOC中,
.
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42,OE+x=8,
解得:x=5,OE=3,
∴半径OA的长=5.
21.证明:连接OA、OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵=,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD,
∴AC=BD.
22.(Ⅰ)证明:∵将△ACM沿直线CE对折,得△DCM,连DN,
∴△DCM≌△ACM(1分)
∴CD=CA,DM=AM,∠DCM=∠ACM,∠CDM=∠A
又∵CA=CB,
∴CD=CB,
∴∠DCN=∠ECF﹣∠DCM=45°﹣∠DCM
∠BCN=∠ACB﹣∠ECF﹣∠ACM
=90°﹣45°﹣∠ACM=45°﹣∠ACM
∴∠DCN=∠BCN
又∵CN=CN,
∴△CDN≌△CBN.
∴DN=BN,∠CDN=∠B.
∴∠MDN=∠CDM+∠CDN=∠A+∠B=90°.
∴在Rt△MDN中,由勾股定理
∴MN2=DM2+DN2,即MN2=AM2+BN2.
(Ⅱ)解:关系式MN2=AM2+BN2仍然成立.
证明:∵将△ACM沿直线CE对折,得△GCM,连GN,
∴△GCM≌△ACM.(8分)
∴CG=CA,GM=AM,∠GCM=∠ACM,∠CGM=∠CAM,
又∵CA=CB,得CG=CB.
∵∠GCN=∠GCM+∠ECF=∠GCM+45°
∴∠BCN=∠ACB﹣∠ACN=90°﹣(∠ECF﹣∠ACM)=45°+∠ACM
得∠GCN=∠BCN.
又∵CN=CN,
∴△CGN≌△CBN.
∴GN=BN,∠CGN=∠B=45°,∠CGM=∠CAM=180°﹣∠CAB=135°,
∴∠MGN=∠CGM﹣∠CGN=135°﹣45°=90°,
∴在Rt△MGN中,由勾股定理,
∴MN2=GM2+GN2,即MN2=AM2+BN2.
1.下列图形中,∠AOB为圆心角的是( )
A.B.C.D.
2.下列语句,错误的是( )
A.直径是弦
B.弦的垂直平分线一定经过圆心
C.相等的圆心角所对的弧相等
D.平分弧的半径垂直于弧所对的弦
3.如图,AB是直径,,∠BOC=40°,则∠AOE的度数为( )
A.30° B.40° C.50° D.60°
4.如图,AB,CD是⊙O的直径,=,若∠AOE=32°,则∠COE的度数是( )
A.32° B.60° C.68° D.64°
5.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
A.8 B.10 C.11 D.12
6.如图,已知点A,B,C均在⊙O上,并且四边形OABC是菱形,那么∠AOC与2∠OAB之间的关系是( )
A.∠AOC>2∠OAB B.∠AOC=2∠OAB C.∠AOC<2∠OAB D.不能确定
7.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD C. D.∠BCA=∠DCA
8.如图,在⊙O中,已知=,则AC与BD的关系是( )
A.AC=BD B.AC<BD C.AC>BD D.不确定
9.如图,在⊙O中,=,∠AOB=40°,则∠ADC的度数是( )
A.40° B.30° C.20° D.15°
10.如图,A,B,C,D均为⊙O上的点,且AB=CD,则下列说法不正确的是( )
A.∠AOB=∠COD B.∠AOC=∠BOD C.AC=BD D.OC=CD
11.如图:AB是所对的弦,AB的中垂线CD分别交于C,交AB于D,AD的中垂线EF分别交于E,交AB于F,DB的中垂线GH分别交于G,交AB于H,下列结论中不正确的是( )
A.= B.= C.= D.EF=GH
12.如图所示,在⊙O中,,∠A=30°,则∠B=( )
A.150° B.75° C.60° D.15°
13.在半径为2cm的⊙O中,弦长为2cm的弦所对的圆心角为( )
A.30° B.60° C.90° D.120°
14.如图,已知:AB是⊙O的直径,C、D是上的三等分点,∠AOE=60°,则∠COE是( )
A.40° B.60° C.80° D.120°
15.在⊙O中,弧AB的度数为60°,则弧AB所对的圆心角的度数为 .
16.AB是⊙O的直径,C,D是上两点,且,,的比为3:2:5(,,弧长之和为),则∠AOC= .
17.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,
则圆柱上M,N两点间的距离是 cm.
18.已知A、B、C是⊙O上的三点,若∠COA=120°,则∠CBA的度数为 .
19.如图,在△ABC中,∠C=90°,∠B=25°,以点C为圆心、AC为半径的圆交AB于点D,则的度数为 度.
20.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
21.如图,已知⊙O的弦AB,E,F是弧AB上两点,=,OE、OF分别交AB于C、D两点,求证:AC=BD.
22.已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN2=AM2+BN2;
(思路点拨:考虑MN2=AM2+BN2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.
参考答案
1.解:根据圆心角定义可知:
A.顶点不是圆心,所以A选项不符合题意;
B.顶点在圆上,∠AOB圆周角,所以B选项不符合题意;
C.∠AOB顶点是圆心,两边与圆相交,所以C选项符合题意;
D.顶点在圆上,∠AOB圆周角,所以D选项不符合题意.
故选:C.
2.解:A、直径为弦,所以A选项的说法正确;
B、弦的垂直平分线一定经过圆心,所以B选项的说法正确;
C、在同圆或等圆中,相等的圆心角所对的弧相等,所以C选项的说法错误;
D、平分弧的半径垂直于弧所对的弦,所以D选项的说法正确.
故选:C.
3.解:∵,∠BOC=40°,
∴∠BOC=∠COD=∠EOD=40°,
∴∠AOE=180°﹣∠BOE=60°.
故选:D.
4.解:∵=,
∴∠BOD=∠AOE=32°,
∵∠BOD=∠AOC,
∴∠AOC=32°
∴∠COE=32°+32°=64°.
故选:D.
5.解:作直径CF,连接BF,如图,
则∠FBC=90°,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴=,
∴DE=BF=6,
∴BC==8.
解法二:如图,过点A作AM⊥BC于M,AN⊥DE于N.
∵AM⊥BC,AN⊥DE,
∴CM=MB,DN=NE=3,
∵AC=AB=AD=AE,
∴∠BAC=2∠MAC,∠EAD=2∠DAN,
∵∠BAC+∠EAD=180°,
∴2∠CAM+2∠DAN=180°,
∴∠CAM+∠DAN=90°,
∵∠ACM+∠CAM=90°,
∴∠ACM=∠DAN,
∵∠AMC=∠AND=90°,
∴△AMC≌△DNA(AAS),
∴AM=DN=3,
∴CM===4,
∴BC=2CM=8.
故选:A.
6.解:连接OB.
∵四边形OABC是菱形,
∴OA=AB,
又∵OA=OB,
∴△OAB是等边三角形.
同理△OBC是等边三角形.
∴∠A=∠AOB=∠BOC=60°,
∴∠AOC=2∠OAB.
故选:B.
7.解:A、∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;
B、∵AC平分∠BAD,∴∠BAC=∠DAC,∴=,∴BC=CD,故本选项正确;
C、∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;
D、∠BCA与∠DCA的大小关系不确定,故本选项错误.
故选:B.
8.解:∵=,
∴,
∴,
∴AC=BD.
故选:A.
9.解:连接CO,如图:
∵在⊙O中,=,
∴∠AOC=∠AOB,
∵∠AOB=40°,
∴∠AOC=40°,
∴∠ADC=∠AOC=20°,
故选:C.
10.解:∵AB=CD,
∴∠AOB=∠COD,故A正确;
∴∠AOB+∠BOC=∠COD+∠BOC,
∴∠AOC=∠BOD,故B正确;
∴AC=BD,故C正确;
∵△OCD不一定是等边三角形,
∴OC不一定等于CD,故D错误.
故选:D.
11.解:连接EG,AE,
∵AB的中垂线CD分别交于C,
∴=,故A正确;
∵AD的中垂线EF分别交于E,交AB于F,DB的中垂线GH分别交于G,
∴=,故B正确;
∴四边形EFHG是矩形,
∴EF=GH,故D正确.
∵AE>AF=DF,
∴AE>EC,
∴>,故C错误.
故选:C.
12.解:∵在⊙O中,,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B==75°(三角形内角和定理).
故选:B.
13.解:如图,∵OA=OB=AB=2,
∴△OAB是等边三角形,
∴∠AOB=60°.
故选:B.
14.解:∵∠AOE=60°,
∴∠BOE=180°﹣∠AOE=120°,
∴的度数是120°,
∵C、D是上的三等分点,
∴弧CD与弧ED的度数都是40度,
∴∠COE=80°.
故选:C.
15.解:∵弧AB的度数为60°,
∴弧AB所对的圆心角的度数为60°,
故答案为:60°.
16.解:∵,,的比为3:2:5(,,弧长之和为),
∴∠AOC:∠COD:∠BOD=3:2:5,
∴∠AOC=×180°=54°.
故答案为54°.
17.解:根据题意得:EF=AD=BC,MN=2EM=EF,
把该正方形纸片卷成一个圆柱,使点A与点D重合,则线段EF形成一直径为10cm的圆,线段EF为圆上的一段弧.
所对的圆心角为:×360°=120°,
所以圆柱上M,N两点间的距离为:2×5×sin60°=5cm.
故答案为:5.
18.解:如图
当B点在优弧AC上,则∠ABC=∠AOC=60°;
当B点在劣弧AC上,即B′点,则∠B′+∠B=180°,
所以∠B′=120°.
故答案为:60°或120°.
19.解:连接CD,∵∠ACB=90°,∠B=25°,∴∠A=90°﹣∠B=65°,
∵CA=CD,∴∠A=∠CDA=65°,∴∠ACD=180°﹣2∠A=50°,
∴弧AD的度数是50度.
20.证明:(1)连接OB、OC,
∵=.
∴AB=AC,
∵OC=OB,OA=OA,
在△AOB与△AOC中,
.
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42,OE+x=8,
解得:x=5,OE=3,
∴半径OA的长=5.
21.证明:连接OA、OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵=,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD,
∴AC=BD.
22.(Ⅰ)证明:∵将△ACM沿直线CE对折,得△DCM,连DN,
∴△DCM≌△ACM(1分)
∴CD=CA,DM=AM,∠DCM=∠ACM,∠CDM=∠A
又∵CA=CB,
∴CD=CB,
∴∠DCN=∠ECF﹣∠DCM=45°﹣∠DCM
∠BCN=∠ACB﹣∠ECF﹣∠ACM
=90°﹣45°﹣∠ACM=45°﹣∠ACM
∴∠DCN=∠BCN
又∵CN=CN,
∴△CDN≌△CBN.
∴DN=BN,∠CDN=∠B.
∴∠MDN=∠CDM+∠CDN=∠A+∠B=90°.
∴在Rt△MDN中,由勾股定理
∴MN2=DM2+DN2,即MN2=AM2+BN2.
(Ⅱ)解:关系式MN2=AM2+BN2仍然成立.
证明:∵将△ACM沿直线CE对折,得△GCM,连GN,
∴△GCM≌△ACM.(8分)
∴CG=CA,GM=AM,∠GCM=∠ACM,∠CGM=∠CAM,
又∵CA=CB,得CG=CB.
∵∠GCN=∠GCM+∠ECF=∠GCM+45°
∴∠BCN=∠ACB﹣∠ACN=90°﹣(∠ECF﹣∠ACM)=45°+∠ACM
得∠GCN=∠BCN.
又∵CN=CN,
∴△CGN≌△CBN.
∴GN=BN,∠CGN=∠B=45°,∠CGM=∠CAM=180°﹣∠CAB=135°,
∴∠MGN=∠CGM﹣∠CGN=135°﹣45°=90°,
∴在Rt△MGN中,由勾股定理,
∴MN2=GM2+GN2,即MN2=AM2+BN2.
