2021-2022学年北师大版九年级数学下册3.3垂径定理 同步经典练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.3垂径定理 同步经典练习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 591.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 19:31:55 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《3-3垂径定理》同步经典练习题(附答案)
1.如图,⊙O的直径AB⊥弦CD于E,若CD=8,BD=2,则AB的长为( )
A.2 B.10 C.12 D.5
2.在直径为10m的圆柱型油槽内注入一些油后,截面如图所示,液面宽AB=6m,如果继续向油槽内注油,使液面宽为8m,那么液面上升了( )m.
A.1 B.2 C.1或7 D.2或6
3.如图,⊙O中弦AB长为8,OC⊥AB,垂足为D,若CD=2,则⊙O半径长是( )
A.10 B.8 C.6 D.5
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=8cm,CD=8cm,则BE为( )
A.1 B.1.5 C.2 D.2.5
5.如图,圆O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP长的取值范围是( )
A.3<OP<5 B.3≤OP≤5 C.4<OP<5 D.4≤OP≤5
6.如图拱桥可以近似地看作直径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,这些钢索中最长的一根的长度为25m,那么其正下方的路面AB的长度为( )
A.100m B.130m C.150m D.180m
7.如图,AB是⊙O的直径,弦CD交AB于点P,AP=3,BP=7,∠APC=30°,则CD的长为( )
A. B.2 C.4 D.8
8.如图,∠ABC=30°,边BA上有一点D,DB=6,以点D为圆心,以DB长为半径作弧交BC于点E,则BE的长是( )
A. B.6 C. D.12
9.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OA=4:5,则DE的长为( )
A.6 B.7 C.8 D.9
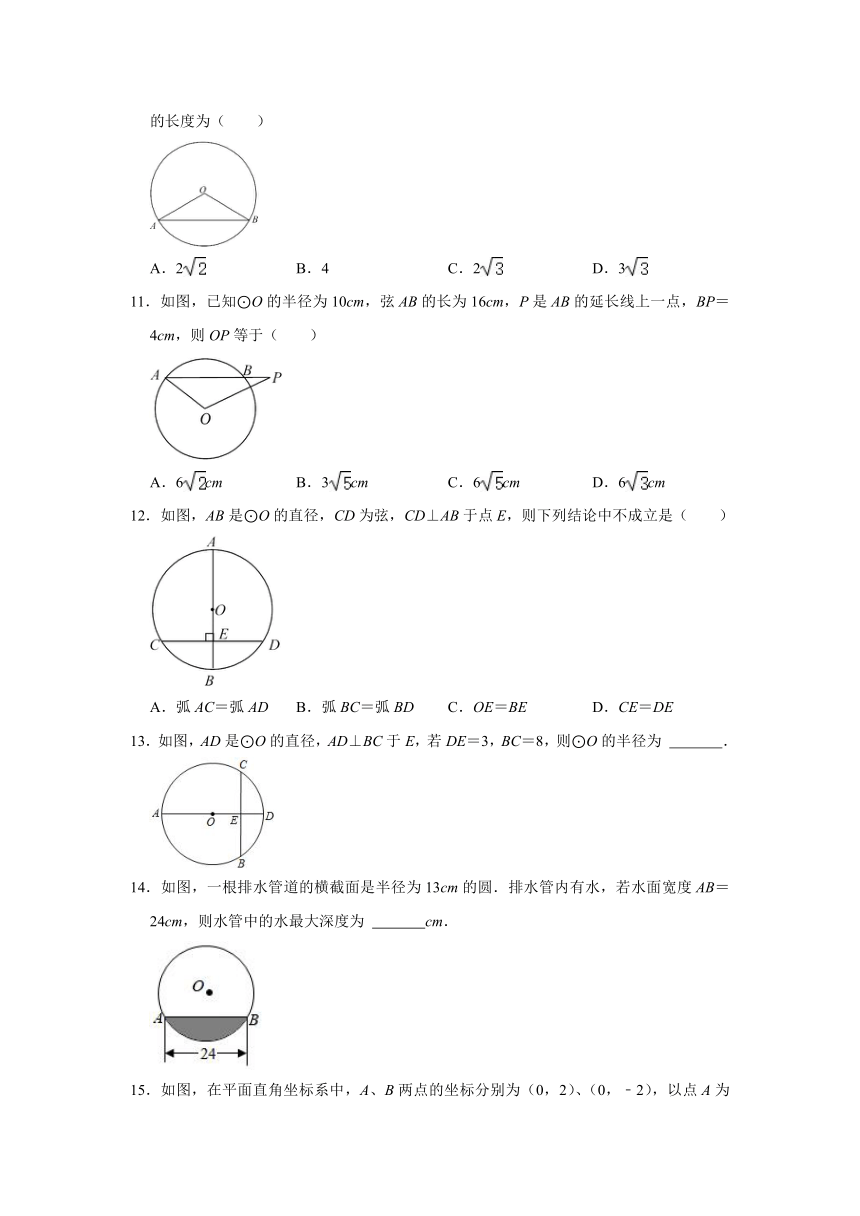
10.如图,在⊙O中,点A,B在圆上,∠AOB=120°,弦AB的长度为4√3,则半径OA的长度为( )
A.2 B.4 C.2 D.3
11.如图,已知⊙O的半径为10cm,弦AB的长为16cm,P是AB的延长线上一点,BP=4cm,则OP等于( )
A.6cm B.3cm C.6cm D.6cm
12.如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立是( )
A.弧AC=弧AD B.弧BC=弧BD C.OE=BE D.CE=DE
13.如图,AD是⊙O的直径,AD⊥BC于E,若DE=3,BC=8,则⊙O的半径为 .
14.如图,一根排水管道的横截面是半径为13cm的圆.排水管内有水,若水面宽度AB=24cm,则水管中的水最大深度为 cm.
15.如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2)、(0,﹣2),以点A为圆心,AB为半径作圆,⊙A与x轴相交于C、D两点,则CD的长度是 .
16.如图,在平面直角坐标系中,圆的半径为5,圆心的坐标为(6,3),圆与横轴的交点分别为A,B,则AB= .
17.如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP,AO分别与⊙O交于B,C两点,若⊙O的半径为3,OP=,则弦BC的最大值为 .
18.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是 .
19.如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则BH的长度为 .
20.如图,在直角坐标系中,一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),C点的坐标为(6,2),写出圆心M点的坐标 .
21.如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是 .
22.如图,已知⊙O的直径AB=4,弦CD⊥AB于点E,点E为OB的中点,点F为圆O上的一个动点,过点A作AG⊥CF于点G,在点F的运动过程中,线段OG长度的最小值为 .
23.如图,AB是⊙O的弦.该图是轴对称图形,它的对称轴是 .
24.如图,用三个边长为2的正方形组成一个轴对称图形,则能将三个正方形完全覆盖的圆的最小半径是 .
25.如图,AB,BC分别是⊙O的两条弦,AO⊥BC,垂足为D,若⊙O的半径为5,BC=8,则AB的长度是 .
26.如图所示,某地有一座圆弧形的拱桥,桥下的水面宽度AB为7.2m,拱顶高出水面(CD)2.4m,现有一艘宽EF为3m且船舱顶部为长方形并高出水面1.5m的货船要经过这里,则货船能顺利通过这座拱桥吗?请作出判断并说明理由.
27.如图,在△ABC中AB=5,AC=4,BC=2,以A为圆心,AB为半径作⊙A,延长BC交⊙A于点D,试求CD的长.
28.如图,有一座圆弧形拱桥,桥下水面宽度AB为16m,拱高(的中点C到弦AB的距离)CD为4m.
(1)求圆弧形拱桥所在圆的半径;
(2)有一艘宽为10m的货船,船舱顶部为长方形,并高出水面2m,则此货船是否能顺利通过此圆弧形拱桥,并说明理由.
29.如图,AB是⊙O的弦,C、D为直线AB上两点,OC=OD,求证:AC=BD.
30.如图所示,一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?
参考答案
1.解:∵AB⊥CD,CD=8,BD=2,
∴DE=CE=4,
∴BE===2,
连接OD,设OD=r,则OE=r﹣2,
在Rt△ODE中,
OD2=OE2+DE2,即r2=(r﹣2)2+42,解得r=5,
∴AB=10.
故选:B.
2.解:设圆柱型油槽的圆心为O,
分两种情况:①AB、GH在圆心O的同侧时,连接OA、OG,过O作OC⊥AB于C,
设GH交OD于E,
依题意得:OA=OG=5(m),AB∥GH,AB=6m,GH=8m,
则OC⊥GH,
由垂径定理,得AC=AB=3(m),EG=GH=4(m),
在Rt△OAC中,由勾股定理得:OC===4(m),
在Rt△OEG中,由勾股定理得:OE===3(m),
∴CE=OC﹣OE=1(m);
②AB、G'H'在圆心O的异侧时,连接OG',过O作OE'⊥G'H'于E',
同①得:OE'=3(m),
∴CE'=OC+OE'=7(m);
综上所述,液面上升了1m或7m,
故选:C.
3.解:连接OA,
设⊙O的半径为r,则OC=OA=r,OE=OC﹣CE=r﹣2,
∵OC⊥AB,AB=8,
∴AE=BE=AB=4,
在Rt△OAE中,由勾股定理得:42+(r﹣2)2=r2,
解得:r=5,
即⊙O的半径长为5,
故选:D.
4.解:∵CD⊥AB,
∴CE=DE=CD=4cm,
设⊙O的半径为rcm,则OC=rcm,OE=(8﹣r)cm,
在Rt△OCE中,(8﹣r)2+42=r2,
解得r=5,
∴OE=8﹣5=3(cm),
∴BE=OB﹣OE=5﹣3=2(cm).
故选:C.
5.解:连接OA,过点O作OH⊥AB于H
则AH=HB=AB=3,
∵圆O的直径为10,
∴OA=5,
由勾股定理得,OH===4,
当点P与点A(或点B)重合时,OP最大,当点P与点H重合时,OP最小,
∴线段OP长的取值范围是4≤OP≤5,
故选:D.
6.解:设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,如图所示:
则OA=OD=×250=125(m),AC=BC=AB,
∴OC=OD﹣CD=125﹣25=100(m),
∴AC===75(m),
∴AB=2AC=150(m),
故选:C.
7.解:过O点作OH⊥CD于H,连接OD,如图,
∵AP=3,BP=7,
∴AB=10,
∴OA=OD=5,OP=2,
∵OH⊥CD,
∴CH=DH,
在Rt△OPH中,∵∠OPH=∠APC=30°,
∴OH=OP=1,
在Rt△ODH中,DH==2,
∴CD=2DH=4.
故选:C.
8.解:过点D作DF⊥BC于F,则BE=2BF,∠BFD=90°,
在Rt△BFD中,∠ABC=30°,BD=6,
∴DF=BD=3,
∴BF=DF=3,
∴BE=2BF=6,
故选:C.
9.解:∵直径AB=10,
∴OA=5,
∵OC:OA=4:5,
∴OC=4,
∵DE⊥AB,
∴CD=CE,
在Rt△OCD中,由勾股定理得:CD===3,
∴DE=2DC=6,
故选:A.
10.解:过O作OC⊥AB于C,
则AC=BC=AB,∠ACO=∠BCO=90°,
∵弦AB的长度为4,
∴AC=BC=2,
∵OA=OB,∠AOB=120°,
∴∠A=∠B=30°,
∴OC=OA,
∵OA2=OC2+AC2,
∴OA2=(OA)2+(2)2,
解得OA=4,
故选:B.
11.解:过O作OC⊥AB于C,
则∠OCP=∠ACO=90°,
∵OC⊥AB,AB=16cm,
∴AC=BC=AB=8(cm),
∵BP=4cm,
∴PC=BC+BP=12(cm),
在Rt△ACO中,由勾股定理得:OC===6(cm),
在Rt△PCO中,由勾股定理得:OP===6(cm),
故选:C.
12.解:∵AB是⊙O的直径,CD为弦,CD⊥AB于点E,
∴=,=,CE=DE,但OE不一定等于BE,
故选项A、B、D正确,选项C不正确,
故选:C.
13.解:连接OC,如图,设⊙O的半径为r,
∵AD⊥BC,
∴CE=BE=BC=4,
在Rt△OCE中,(r﹣3)2+42=r2,
解得r=.
即⊙O的半径为.
故答案为:
14.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵OB=OC=13cm,
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水管中的水最大深度为8cm,
故答案为:8.
15.解:∵A、B两点的坐标分别为(0,2)、(0,﹣2),
∴OA=2,OB=2,
则AB=4,
在Rt△AOC中,OC==2,
∵AB⊥CD,
∴CD=2OC=4,
故答案为:4.
16.解:过圆心P作PH⊥AB于H,连接PA,如图,则AH=BH,
∵P(6,3),
∴PH=3,
在Rt△PAH中,PA=5,PH=3,
∴AH==4,
∴AB=2AH=8.
故答案为:8.
17.解:如图,过点O作OE⊥AB于E,
∵O为圆心,
∴AE=BE,
∴OE=BC,
∵OE≤OP,
∴BC≤2OP,
∴当E、P重合时,即OP垂直AB时,BC取最大值,
∴弦BC的最大值为:2OP=2,
故答案为:2.
18.解:如图,作△AEC的外接圆⊙O′,延长BC交⊙O′于D2R,连接AR,则AR是直径,连接OO′,EO′.
∵EC⊥CD,
∴∠ECD=90°,
∵AB是直径,
∴∠ACB=90°,
∴BC===4,
∵∠D+∠DEC=90°,∠B+∠BAC=90°,∠B=∠D,
∴∠DEC=∠BAC=定值,
∴∠AEC是定值,
∴点E的运动轨迹是,
∵∠R+∠AEC=180°,∠AEC+∠DEC=180°,
∴∠R=∠DEC=∠BAC,
∴∠R+∠B=90°,
∴∠BAR=90°,
∵∠B=∠B,∠ACB=∠BAR=90°,
∴△BCA∽△BAR,
∴=,
∴=,
∴BR=,
∴CR=BR﹣BC=,
∴AR===,
∴EO′=AR=,
∵AO=OB,AO′=O′R,
∴OO′=BR=,
∵OE≥OO′﹣EO′=﹣=,
∴OE的最小值为.
故答案为:.
19.解:连接OC,
∵CD⊥AB,CD=8,
∴CH=DH=CD=4,∠OHC=90°,
∵直径AB=10,
∴OB=OC=5,
在Rt△OCH中,OH===3,
∴BH=OB﹣OH=2,
故答案为:2.
20.解:作BC的垂直平分线,交AB的垂直平分线于M,如图,
则圆心M点的坐标为(2,0),
故答案为:(2,0).
21.解:∵OE⊥AC,
∴AE=EC,
∵AB⊥CD,
∴∠AFC=∠AEO=90°,
∵OE=3,OB=5,
∴AE===4,
∴AC=8,
∵∠A=∠A,∠AEO=∠AFC,
∴△AEO∽△AFC,
∴=,即=,
解得:FC=,
∵CD⊥AB,
∴CD=2CF=,
故答案为:.
22.解:如图,连接OC,CB,取AC的中点T,连接OT,TG.
∵AB⊥CD,OE=EB,
∴CO=CB,
∵OC=OB,
∴OC=OB=CB=2,
∴∠B=60°,
∵AB是直径,
∴∠ACB=90°,
∴AC=AB sin60°=2,
∵AT=CT,AO=OB,
∴OT=BC=1,
∵AG⊥CF,
∴∠CGA=90°,
∴TG=AC=,
∵OG≥TG﹣OT=﹣1,
∴OG的最小值为﹣1.
故答案为:﹣1.
23.解:
过O作直线MN⊥AB于C,
∵MN过圆心O,MN⊥AB,
∴AC=BC,
即直线MN是线段AB的对称轴,
∴该图形的对称轴是直线MN(即是过圆心O且垂直于线段AB的直线),
故答案为:过圆心O且垂直于线段AB的直线.
24.解:如图,连接OC,OD,延长BO交上面的正方形与点A,设定圆心与上面正方形的距离为x,
则BO=2﹣x,BC=2,AD=1,AO=2+x,
由勾股定理得:BC2+BO2=AD2+AO2,即22+(2﹣x)2=(2+x)2+12,
解得:x=,
所以能将其完全覆盖的圆的最小半径R2=2+(2﹣x)2,
解得:R=.
故答案为:.
25.解:连接OB,如图所示:
∵AO⊥BC,BC=8,
∴BD=BC=4,OB=5,∠ODB=90°,
∵⊙O的半径为5,
∴OB=5,
∴OD===3,
∴AD=OA+OD=5+3=8,
在Rt△ADB中,由勾股定理得:AB===4,
故答案为:4.
26.解:货船能顺利通过这座拱桥,理由如下:
如图,连接ON、OA.
∵OC⊥AB,AB=7.2m,
∴AD=AB=3.6(m),
设OB=OC=ON=rm,则OD=(r﹣2.4)m,
在Rt△AOD中,根据勾股定理得:r2=(r﹣2.4)2+3.62,
解得:r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面1.5m,
∴CH=2.4﹣1.5=0.9(m),
∴OH=3.9﹣0.9=3(m),
在Rt△OHN中,HN2=ON2﹣OH2=3.92﹣32=6.21(m2),
∴HN=(m),
∴MN=2HN=2(m)>3m,
∴货船能顺利通过这座拱桥.
27.解:过点A作AE⊥BD于点E,连接AD,如图,则DE=BE,
在Rt△ACE中,AE2=AC2﹣CE2,
在Rt△ABE中,AE2=AB2﹣BE2,
∴AC2﹣CE2=AB2﹣BE2,
即42﹣(BE﹣2)2=52﹣BE2,
解得BE=,
∴CD=BD﹣BC=2BE﹣2=2×﹣2=.
答:CD的长为.
28.解:(1)如图,连接ON,OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=16m,
∴BD=AB=8m.
又∵CD=4m,
设OB=OC=ON=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+82,
解得r=10,
∴圆的半径为10m.
(2)此货船能顺利通过这座拱桥.
理由:∵CD=4m,船舱顶部为长方形并高出水面2m,
∴CE=4﹣2=2(m),
∴OE=r﹣CE=10﹣2=8(m),
在Rt△OEN中,EN2=ON2﹣OE2=102﹣82=36,
∴EN=6(m).
∴MN=2EN=2×6=12>10.
∴此货船能顺利通过这座拱桥.
29.证明:作OH⊥AB于H,如图,
则AH=BH,
∵OC=OD,OH⊥AB,
∴CH=DH,
∴CH﹣AH=DH﹣BH,
即AC=BD.
30.解:∵车宽1.6米,
∴卡车能否通过,只要比较距厂门中线0.8米处的高度与车高.
在Rt△OCD中,由勾股定理可得:
CD===0.6(m),
CH=CD+DH=0.6+2.3=2.9>2.5,
∴卡车能通过此门.
1.如图,⊙O的直径AB⊥弦CD于E,若CD=8,BD=2,则AB的长为( )
A.2 B.10 C.12 D.5
2.在直径为10m的圆柱型油槽内注入一些油后,截面如图所示,液面宽AB=6m,如果继续向油槽内注油,使液面宽为8m,那么液面上升了( )m.
A.1 B.2 C.1或7 D.2或6
3.如图,⊙O中弦AB长为8,OC⊥AB,垂足为D,若CD=2,则⊙O半径长是( )
A.10 B.8 C.6 D.5
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=8cm,CD=8cm,则BE为( )
A.1 B.1.5 C.2 D.2.5
5.如图,圆O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP长的取值范围是( )
A.3<OP<5 B.3≤OP≤5 C.4<OP<5 D.4≤OP≤5
6.如图拱桥可以近似地看作直径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,这些钢索中最长的一根的长度为25m,那么其正下方的路面AB的长度为( )
A.100m B.130m C.150m D.180m
7.如图,AB是⊙O的直径,弦CD交AB于点P,AP=3,BP=7,∠APC=30°,则CD的长为( )
A. B.2 C.4 D.8
8.如图,∠ABC=30°,边BA上有一点D,DB=6,以点D为圆心,以DB长为半径作弧交BC于点E,则BE的长是( )
A. B.6 C. D.12
9.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OA=4:5,则DE的长为( )
A.6 B.7 C.8 D.9
10.如图,在⊙O中,点A,B在圆上,∠AOB=120°,弦AB的长度为4√3,则半径OA的长度为( )
A.2 B.4 C.2 D.3
11.如图,已知⊙O的半径为10cm,弦AB的长为16cm,P是AB的延长线上一点,BP=4cm,则OP等于( )
A.6cm B.3cm C.6cm D.6cm
12.如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立是( )
A.弧AC=弧AD B.弧BC=弧BD C.OE=BE D.CE=DE
13.如图,AD是⊙O的直径,AD⊥BC于E,若DE=3,BC=8,则⊙O的半径为 .
14.如图,一根排水管道的横截面是半径为13cm的圆.排水管内有水,若水面宽度AB=24cm,则水管中的水最大深度为 cm.
15.如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2)、(0,﹣2),以点A为圆心,AB为半径作圆,⊙A与x轴相交于C、D两点,则CD的长度是 .
16.如图,在平面直角坐标系中,圆的半径为5,圆心的坐标为(6,3),圆与横轴的交点分别为A,B,则AB= .
17.如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP,AO分别与⊙O交于B,C两点,若⊙O的半径为3,OP=,则弦BC的最大值为 .
18.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是 .
19.如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则BH的长度为 .
20.如图,在直角坐标系中,一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),C点的坐标为(6,2),写出圆心M点的坐标 .
21.如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是 .
22.如图,已知⊙O的直径AB=4,弦CD⊥AB于点E,点E为OB的中点,点F为圆O上的一个动点,过点A作AG⊥CF于点G,在点F的运动过程中,线段OG长度的最小值为 .
23.如图,AB是⊙O的弦.该图是轴对称图形,它的对称轴是 .
24.如图,用三个边长为2的正方形组成一个轴对称图形,则能将三个正方形完全覆盖的圆的最小半径是 .
25.如图,AB,BC分别是⊙O的两条弦,AO⊥BC,垂足为D,若⊙O的半径为5,BC=8,则AB的长度是 .
26.如图所示,某地有一座圆弧形的拱桥,桥下的水面宽度AB为7.2m,拱顶高出水面(CD)2.4m,现有一艘宽EF为3m且船舱顶部为长方形并高出水面1.5m的货船要经过这里,则货船能顺利通过这座拱桥吗?请作出判断并说明理由.
27.如图,在△ABC中AB=5,AC=4,BC=2,以A为圆心,AB为半径作⊙A,延长BC交⊙A于点D,试求CD的长.
28.如图,有一座圆弧形拱桥,桥下水面宽度AB为16m,拱高(的中点C到弦AB的距离)CD为4m.
(1)求圆弧形拱桥所在圆的半径;
(2)有一艘宽为10m的货船,船舱顶部为长方形,并高出水面2m,则此货船是否能顺利通过此圆弧形拱桥,并说明理由.
29.如图,AB是⊙O的弦,C、D为直线AB上两点,OC=OD,求证:AC=BD.
30.如图所示,一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?
参考答案
1.解:∵AB⊥CD,CD=8,BD=2,
∴DE=CE=4,
∴BE===2,
连接OD,设OD=r,则OE=r﹣2,
在Rt△ODE中,
OD2=OE2+DE2,即r2=(r﹣2)2+42,解得r=5,
∴AB=10.
故选:B.
2.解:设圆柱型油槽的圆心为O,
分两种情况:①AB、GH在圆心O的同侧时,连接OA、OG,过O作OC⊥AB于C,
设GH交OD于E,
依题意得:OA=OG=5(m),AB∥GH,AB=6m,GH=8m,
则OC⊥GH,
由垂径定理,得AC=AB=3(m),EG=GH=4(m),
在Rt△OAC中,由勾股定理得:OC===4(m),
在Rt△OEG中,由勾股定理得:OE===3(m),
∴CE=OC﹣OE=1(m);
②AB、G'H'在圆心O的异侧时,连接OG',过O作OE'⊥G'H'于E',
同①得:OE'=3(m),
∴CE'=OC+OE'=7(m);
综上所述,液面上升了1m或7m,
故选:C.
3.解:连接OA,
设⊙O的半径为r,则OC=OA=r,OE=OC﹣CE=r﹣2,
∵OC⊥AB,AB=8,
∴AE=BE=AB=4,
在Rt△OAE中,由勾股定理得:42+(r﹣2)2=r2,
解得:r=5,
即⊙O的半径长为5,
故选:D.
4.解:∵CD⊥AB,
∴CE=DE=CD=4cm,
设⊙O的半径为rcm,则OC=rcm,OE=(8﹣r)cm,
在Rt△OCE中,(8﹣r)2+42=r2,
解得r=5,
∴OE=8﹣5=3(cm),
∴BE=OB﹣OE=5﹣3=2(cm).
故选:C.
5.解:连接OA,过点O作OH⊥AB于H
则AH=HB=AB=3,
∵圆O的直径为10,
∴OA=5,
由勾股定理得,OH===4,
当点P与点A(或点B)重合时,OP最大,当点P与点H重合时,OP最小,
∴线段OP长的取值范围是4≤OP≤5,
故选:D.
6.解:设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,如图所示:
则OA=OD=×250=125(m),AC=BC=AB,
∴OC=OD﹣CD=125﹣25=100(m),
∴AC===75(m),
∴AB=2AC=150(m),
故选:C.
7.解:过O点作OH⊥CD于H,连接OD,如图,
∵AP=3,BP=7,
∴AB=10,
∴OA=OD=5,OP=2,
∵OH⊥CD,
∴CH=DH,
在Rt△OPH中,∵∠OPH=∠APC=30°,
∴OH=OP=1,
在Rt△ODH中,DH==2,
∴CD=2DH=4.
故选:C.
8.解:过点D作DF⊥BC于F,则BE=2BF,∠BFD=90°,
在Rt△BFD中,∠ABC=30°,BD=6,
∴DF=BD=3,
∴BF=DF=3,
∴BE=2BF=6,
故选:C.
9.解:∵直径AB=10,
∴OA=5,
∵OC:OA=4:5,
∴OC=4,
∵DE⊥AB,
∴CD=CE,
在Rt△OCD中,由勾股定理得:CD===3,
∴DE=2DC=6,
故选:A.
10.解:过O作OC⊥AB于C,
则AC=BC=AB,∠ACO=∠BCO=90°,
∵弦AB的长度为4,
∴AC=BC=2,
∵OA=OB,∠AOB=120°,
∴∠A=∠B=30°,
∴OC=OA,
∵OA2=OC2+AC2,
∴OA2=(OA)2+(2)2,
解得OA=4,
故选:B.
11.解:过O作OC⊥AB于C,
则∠OCP=∠ACO=90°,
∵OC⊥AB,AB=16cm,
∴AC=BC=AB=8(cm),
∵BP=4cm,
∴PC=BC+BP=12(cm),
在Rt△ACO中,由勾股定理得:OC===6(cm),
在Rt△PCO中,由勾股定理得:OP===6(cm),
故选:C.
12.解:∵AB是⊙O的直径,CD为弦,CD⊥AB于点E,
∴=,=,CE=DE,但OE不一定等于BE,
故选项A、B、D正确,选项C不正确,
故选:C.
13.解:连接OC,如图,设⊙O的半径为r,
∵AD⊥BC,
∴CE=BE=BC=4,
在Rt△OCE中,(r﹣3)2+42=r2,
解得r=.
即⊙O的半径为.
故答案为:
14.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵OB=OC=13cm,
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水管中的水最大深度为8cm,
故答案为:8.
15.解:∵A、B两点的坐标分别为(0,2)、(0,﹣2),
∴OA=2,OB=2,
则AB=4,
在Rt△AOC中,OC==2,
∵AB⊥CD,
∴CD=2OC=4,
故答案为:4.
16.解:过圆心P作PH⊥AB于H,连接PA,如图,则AH=BH,
∵P(6,3),
∴PH=3,
在Rt△PAH中,PA=5,PH=3,
∴AH==4,
∴AB=2AH=8.
故答案为:8.
17.解:如图,过点O作OE⊥AB于E,
∵O为圆心,
∴AE=BE,
∴OE=BC,
∵OE≤OP,
∴BC≤2OP,
∴当E、P重合时,即OP垂直AB时,BC取最大值,
∴弦BC的最大值为:2OP=2,
故答案为:2.
18.解:如图,作△AEC的外接圆⊙O′,延长BC交⊙O′于D2R,连接AR,则AR是直径,连接OO′,EO′.
∵EC⊥CD,
∴∠ECD=90°,
∵AB是直径,
∴∠ACB=90°,
∴BC===4,
∵∠D+∠DEC=90°,∠B+∠BAC=90°,∠B=∠D,
∴∠DEC=∠BAC=定值,
∴∠AEC是定值,
∴点E的运动轨迹是,
∵∠R+∠AEC=180°,∠AEC+∠DEC=180°,
∴∠R=∠DEC=∠BAC,
∴∠R+∠B=90°,
∴∠BAR=90°,
∵∠B=∠B,∠ACB=∠BAR=90°,
∴△BCA∽△BAR,
∴=,
∴=,
∴BR=,
∴CR=BR﹣BC=,
∴AR===,
∴EO′=AR=,
∵AO=OB,AO′=O′R,
∴OO′=BR=,
∵OE≥OO′﹣EO′=﹣=,
∴OE的最小值为.
故答案为:.
19.解:连接OC,
∵CD⊥AB,CD=8,
∴CH=DH=CD=4,∠OHC=90°,
∵直径AB=10,
∴OB=OC=5,
在Rt△OCH中,OH===3,
∴BH=OB﹣OH=2,
故答案为:2.
20.解:作BC的垂直平分线,交AB的垂直平分线于M,如图,
则圆心M点的坐标为(2,0),
故答案为:(2,0).
21.解:∵OE⊥AC,
∴AE=EC,
∵AB⊥CD,
∴∠AFC=∠AEO=90°,
∵OE=3,OB=5,
∴AE===4,
∴AC=8,
∵∠A=∠A,∠AEO=∠AFC,
∴△AEO∽△AFC,
∴=,即=,
解得:FC=,
∵CD⊥AB,
∴CD=2CF=,
故答案为:.
22.解:如图,连接OC,CB,取AC的中点T,连接OT,TG.
∵AB⊥CD,OE=EB,
∴CO=CB,
∵OC=OB,
∴OC=OB=CB=2,
∴∠B=60°,
∵AB是直径,
∴∠ACB=90°,
∴AC=AB sin60°=2,
∵AT=CT,AO=OB,
∴OT=BC=1,
∵AG⊥CF,
∴∠CGA=90°,
∴TG=AC=,
∵OG≥TG﹣OT=﹣1,
∴OG的最小值为﹣1.
故答案为:﹣1.
23.解:
过O作直线MN⊥AB于C,
∵MN过圆心O,MN⊥AB,
∴AC=BC,
即直线MN是线段AB的对称轴,
∴该图形的对称轴是直线MN(即是过圆心O且垂直于线段AB的直线),
故答案为:过圆心O且垂直于线段AB的直线.
24.解:如图,连接OC,OD,延长BO交上面的正方形与点A,设定圆心与上面正方形的距离为x,
则BO=2﹣x,BC=2,AD=1,AO=2+x,
由勾股定理得:BC2+BO2=AD2+AO2,即22+(2﹣x)2=(2+x)2+12,
解得:x=,
所以能将其完全覆盖的圆的最小半径R2=2+(2﹣x)2,
解得:R=.
故答案为:.
25.解:连接OB,如图所示:
∵AO⊥BC,BC=8,
∴BD=BC=4,OB=5,∠ODB=90°,
∵⊙O的半径为5,
∴OB=5,
∴OD===3,
∴AD=OA+OD=5+3=8,
在Rt△ADB中,由勾股定理得:AB===4,
故答案为:4.
26.解:货船能顺利通过这座拱桥,理由如下:
如图,连接ON、OA.
∵OC⊥AB,AB=7.2m,
∴AD=AB=3.6(m),
设OB=OC=ON=rm,则OD=(r﹣2.4)m,
在Rt△AOD中,根据勾股定理得:r2=(r﹣2.4)2+3.62,
解得:r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面1.5m,
∴CH=2.4﹣1.5=0.9(m),
∴OH=3.9﹣0.9=3(m),
在Rt△OHN中,HN2=ON2﹣OH2=3.92﹣32=6.21(m2),
∴HN=(m),
∴MN=2HN=2(m)>3m,
∴货船能顺利通过这座拱桥.
27.解:过点A作AE⊥BD于点E,连接AD,如图,则DE=BE,
在Rt△ACE中,AE2=AC2﹣CE2,
在Rt△ABE中,AE2=AB2﹣BE2,
∴AC2﹣CE2=AB2﹣BE2,
即42﹣(BE﹣2)2=52﹣BE2,
解得BE=,
∴CD=BD﹣BC=2BE﹣2=2×﹣2=.
答:CD的长为.
28.解:(1)如图,连接ON,OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=16m,
∴BD=AB=8m.
又∵CD=4m,
设OB=OC=ON=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+82,
解得r=10,
∴圆的半径为10m.
(2)此货船能顺利通过这座拱桥.
理由:∵CD=4m,船舱顶部为长方形并高出水面2m,
∴CE=4﹣2=2(m),
∴OE=r﹣CE=10﹣2=8(m),
在Rt△OEN中,EN2=ON2﹣OE2=102﹣82=36,
∴EN=6(m).
∴MN=2EN=2×6=12>10.
∴此货船能顺利通过这座拱桥.
29.证明:作OH⊥AB于H,如图,
则AH=BH,
∵OC=OD,OH⊥AB,
∴CH=DH,
∴CH﹣AH=DH﹣BH,
即AC=BD.
30.解:∵车宽1.6米,
∴卡车能否通过,只要比较距厂门中线0.8米处的高度与车高.
在Rt△OCD中,由勾股定理可得:
CD===0.6(m),
CH=CD+DH=0.6+2.3=2.9>2.5,
∴卡车能通过此门.
