6.3 实践与探索(1) 课件(共25张PPT)
文档属性
| 名称 | 6.3 实践与探索(1) 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 07:24:50 | ||
图片预览








文档简介
(共25张PPT)
2022年春华师大版数学
七年级下册数学精品课件
实践与探索(1)
学习目标
理解并掌握行程问题中常见的数量关系.
根据行程问题中的数量关系列一元一次方程解决实际问题,并掌握解此类问题的一般思路.
用方程解决实际问题的过程
问题
方程
过程
分析
抽象
求解
检验
其中分析和抽象的过程通常包括:
1.弄清题意和其中的数量关系,用字母表示适当的未知数(设元);
2.找出问题所给的等量关系,它反映了未知量与已知量之间的关系;
3.对这个等量关系中涉及的量,列出所需的代数式,根据等量关系,列出方程。
在设未知数和做出解答时,应注意量的单位。
复习回顾
复习回顾
2.行程问题中常见的量都有什么?
路程=速度×时间 速度=时间=
路程 速度 时间
3.行程问题中常见的量之间的数量关系是什么?
1.行程问题常见题型?
相向而行---相遇问题 同向而行---追击问题
1.甲、乙两地相距x千米,小王每小时行4千米,小李每时比小王多行1千米,从甲地到乙地,小李比小王少用___________小时
2.某人从甲地到乙地,全程的1/2乘车,全程的1/3乘船,最后双步行5千米到达乙地,问甲、乙两地间的路程是多少千米?
解:设甲、乙两地间的路程为x千米,那么乘车路程为___千米,乘船路程为___千米,
根据题意得,可列出方程________________.
针对练习
小张和父亲预定搭乘家门口的公共汽车赶往火车站,去家乡看望爷爷.在行驶了1/3路程时,小张向司机询问到达火车站的时间,司机估计继续乘公共汽车到火车站时火车将正好开出,根据司机的建议,小张和父亲随即下车改乘出租车,车速提高了一倍,结果赶在火车开车前45分钟到达火车站,已知公共汽车的平均速度是40千米/时.
问小张家到火车站有多远?
典例解析
思考:题 中 有 哪 一 些 等 量 关 系?
不换车使用的时间 - 换车使用的时间= 提前时间
解法1:设乘公共汽车实际上行驶了x千米,
由题意可知
解这个方程:
经检验,它符合题意
答:小张家到火车站有90千米.
典例解析
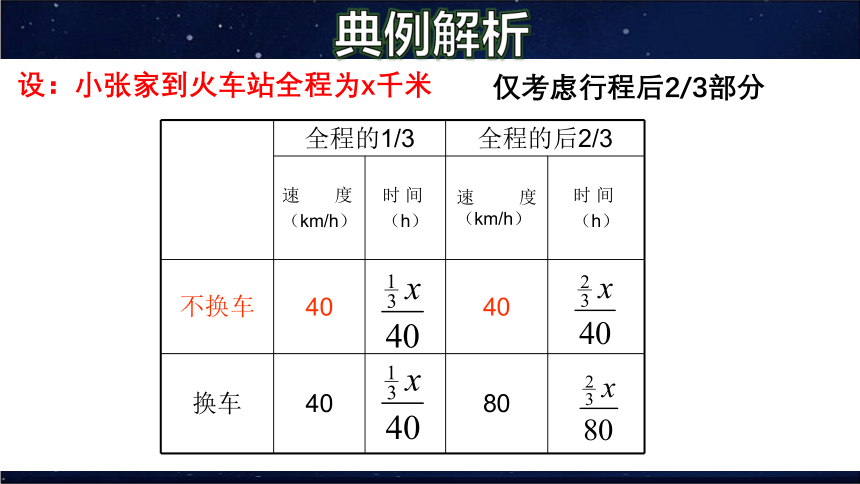
设:小张家到火车站全程为x千米
时 间
(h)
时 间
(h)
速 度(km/h)
速 度
(km/h)
80
40
换车
40
40
不换车
全程的后2/3
全程的1/3
仅考虑行程后2/3部分
典例解析
解法2:设小张家到火车站全 程为x千米,
由题意可知
解这个方程:
经检验,它符合题意
答:小张家到火车站有90千米.
典例解析
是否有其他设未知数
的方法?
设时间为未知数行吗?
【方法归纳】对于一些实际问题,我们可以从不同的角度寻找相等关系,设出合适的未知数,列出不同的方程来解.
设:公共汽车实际行驶x小时
x小时
2x小时
x小时
公共汽车
出租车
时 间
(h)
时 间
(h)
速 度(km/h)
速 度
(km/h)
80
40
换车
40
40
不换车
全程的后2/3
全程的1/3
x
x
2x
典例解析
解法3:
解得:
答:小张家到火车站有90千米.
设公共汽车实际行驶x小时
经检验,它符合题意
典例解析
思考:
1.上述几种解法有什么不同?
2.在解行程问题时可借助那些方法解题?
在解应用题时通常有二种设法:
在解行程问题时通常借助________________进行解题.
直接设法与间接设法
行程图与列表
总结提升
1.为庆祝校运会开幕,初一(2)班接受了制作小旗的任务,原计划一半同学参加制作,每天制作40面,完成了二分之一以后,全班同学一起参加,结果比原计划提前一天半完成任务,假设每人的制作效率相同,问共制作小旗多少面?
解:设共制作小旗x面
解得:
答:共制作小旗480面.
达标检测
2.小明每天早上要在7:30分之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现他忘了带数学书.于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他,问爸爸追上小明用了多长时间
则有5×80+80X=180X
追上
小明5分钟走的路程
小明在爸爸追时走的路程
爸爸追赶小明时走的路程
追上时,距学校还有多远
解得X=4
280千米
家
学校
达标检测
3.一队学生从甲地去乙地,速度为每4km当行进1km后,一学生奉命以每时5km的速度跑步回甲地取东西,然后又以同样速度追赶队伍,结果在距乙地2km处追上队伍,求甲、乙两地的距离?
解:设甲、乙两地距离x千米
1km
2km
(X-3)km
解得:x=11
答:甲、乙两地的距离为11km.
经检验,它符合题意
达标检测
4.兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
解:设两人所跑的路程为x米.根据题意列方程,得:
解得: x=3000
答:两人所跑的路程为3000米.
还有别的方法吗?
达标检测
5.甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
解:设甲经过x秒后追上乙,则依题意可得
6.5×(x+1)=7x
解得:x=13
答:甲经过13秒后追上乙.
达标检测
6.甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
解:设x小时快车才能追上慢车,根据题意列方程,得:
85x-65x=450
解得: x=22.5
答: 22.5小时快车才能追上慢车.
达标检测
7.甲乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km;一列快车从乙站开出,每小时行驶85km.快车先开1小时,两车相向而行,慢车行使了多少小时两车相遇?
解:慢车行使了x小时两车相遇,根据题意列方程,得:
85(x+1)+65x=450
解得: x=
答:慢车行使了小时两车相遇.
达标检测
8.一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24)km/h.
根据题意,得 .
解得 x=840.
两城市的距离为3×(840-24)=2448 (km).
答:两城市之间的距离为2448 km.
达标检测
9.运动场的跑道一圈长400m,甲练习骑自行车,平均每分骑350m,乙练习跑步,平均每分跑250m.两人从同一处同时同向出发,经过多少时间首次相遇?
解:设经过x分钟首次相遇,根据题意列方程,得:
350x-250x=400
解得: x=4
答:经过4分钟甲、乙相遇.
达标检测
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
七年级下册数学精品课件
实践与探索(1)
学习目标
理解并掌握行程问题中常见的数量关系.
根据行程问题中的数量关系列一元一次方程解决实际问题,并掌握解此类问题的一般思路.
用方程解决实际问题的过程
问题
方程
过程
分析
抽象
求解
检验
其中分析和抽象的过程通常包括:
1.弄清题意和其中的数量关系,用字母表示适当的未知数(设元);
2.找出问题所给的等量关系,它反映了未知量与已知量之间的关系;
3.对这个等量关系中涉及的量,列出所需的代数式,根据等量关系,列出方程。
在设未知数和做出解答时,应注意量的单位。
复习回顾
复习回顾
2.行程问题中常见的量都有什么?
路程=速度×时间 速度=时间=
路程 速度 时间
3.行程问题中常见的量之间的数量关系是什么?
1.行程问题常见题型?
相向而行---相遇问题 同向而行---追击问题
1.甲、乙两地相距x千米,小王每小时行4千米,小李每时比小王多行1千米,从甲地到乙地,小李比小王少用___________小时
2.某人从甲地到乙地,全程的1/2乘车,全程的1/3乘船,最后双步行5千米到达乙地,问甲、乙两地间的路程是多少千米?
解:设甲、乙两地间的路程为x千米,那么乘车路程为___千米,乘船路程为___千米,
根据题意得,可列出方程________________.
针对练习
小张和父亲预定搭乘家门口的公共汽车赶往火车站,去家乡看望爷爷.在行驶了1/3路程时,小张向司机询问到达火车站的时间,司机估计继续乘公共汽车到火车站时火车将正好开出,根据司机的建议,小张和父亲随即下车改乘出租车,车速提高了一倍,结果赶在火车开车前45分钟到达火车站,已知公共汽车的平均速度是40千米/时.
问小张家到火车站有多远?
典例解析
思考:题 中 有 哪 一 些 等 量 关 系?
不换车使用的时间 - 换车使用的时间= 提前时间
解法1:设乘公共汽车实际上行驶了x千米,
由题意可知
解这个方程:
经检验,它符合题意
答:小张家到火车站有90千米.
典例解析
设:小张家到火车站全程为x千米
时 间
(h)
时 间
(h)
速 度(km/h)
速 度
(km/h)
80
40
换车
40
40
不换车
全程的后2/3
全程的1/3
仅考虑行程后2/3部分
典例解析
解法2:设小张家到火车站全 程为x千米,
由题意可知
解这个方程:
经检验,它符合题意
答:小张家到火车站有90千米.
典例解析
是否有其他设未知数
的方法?
设时间为未知数行吗?
【方法归纳】对于一些实际问题,我们可以从不同的角度寻找相等关系,设出合适的未知数,列出不同的方程来解.
设:公共汽车实际行驶x小时
x小时
2x小时
x小时
公共汽车
出租车
时 间
(h)
时 间
(h)
速 度(km/h)
速 度
(km/h)
80
40
换车
40
40
不换车
全程的后2/3
全程的1/3
x
x
2x
典例解析
解法3:
解得:
答:小张家到火车站有90千米.
设公共汽车实际行驶x小时
经检验,它符合题意
典例解析
思考:
1.上述几种解法有什么不同?
2.在解行程问题时可借助那些方法解题?
在解应用题时通常有二种设法:
在解行程问题时通常借助________________进行解题.
直接设法与间接设法
行程图与列表
总结提升
1.为庆祝校运会开幕,初一(2)班接受了制作小旗的任务,原计划一半同学参加制作,每天制作40面,完成了二分之一以后,全班同学一起参加,结果比原计划提前一天半完成任务,假设每人的制作效率相同,问共制作小旗多少面?
解:设共制作小旗x面
解得:
答:共制作小旗480面.
达标检测
2.小明每天早上要在7:30分之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现他忘了带数学书.于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他,问爸爸追上小明用了多长时间
则有5×80+80X=180X
追上
小明5分钟走的路程
小明在爸爸追时走的路程
爸爸追赶小明时走的路程
追上时,距学校还有多远
解得X=4
280千米
家
学校
达标检测
3.一队学生从甲地去乙地,速度为每4km当行进1km后,一学生奉命以每时5km的速度跑步回甲地取东西,然后又以同样速度追赶队伍,结果在距乙地2km处追上队伍,求甲、乙两地的距离?
解:设甲、乙两地距离x千米
1km
2km
(X-3)km
解得:x=11
答:甲、乙两地的距离为11km.
经检验,它符合题意
达标检测
4.兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
解:设两人所跑的路程为x米.根据题意列方程,得:
解得: x=3000
答:两人所跑的路程为3000米.
还有别的方法吗?
达标检测
5.甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
解:设甲经过x秒后追上乙,则依题意可得
6.5×(x+1)=7x
解得:x=13
答:甲经过13秒后追上乙.
达标检测
6.甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
解:设x小时快车才能追上慢车,根据题意列方程,得:
85x-65x=450
解得: x=22.5
答: 22.5小时快车才能追上慢车.
达标检测
7.甲乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km;一列快车从乙站开出,每小时行驶85km.快车先开1小时,两车相向而行,慢车行使了多少小时两车相遇?
解:慢车行使了x小时两车相遇,根据题意列方程,得:
85(x+1)+65x=450
解得: x=
答:慢车行使了小时两车相遇.
达标检测
8.一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24)km/h.
根据题意,得 .
解得 x=840.
两城市的距离为3×(840-24)=2448 (km).
答:两城市之间的距离为2448 km.
达标检测
9.运动场的跑道一圈长400m,甲练习骑自行车,平均每分骑350m,乙练习跑步,平均每分跑250m.两人从同一处同时同向出发,经过多少时间首次相遇?
解:设经过x分钟首次相遇,根据题意列方程,得:
350x-250x=400
解得: x=4
答:经过4分钟甲、乙相遇.
达标检测
https://www.21cnjy.com/help/help_extract.php
