2021-2022学年苏科版七年级数学下册7.2探索平行线的性质同步习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7.2探索平行线的性质同步习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 397.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 19:31:59 | ||
图片预览




文档简介
苏科版数学七年级下册第7章7.2探索平行线的性质
一、选择题
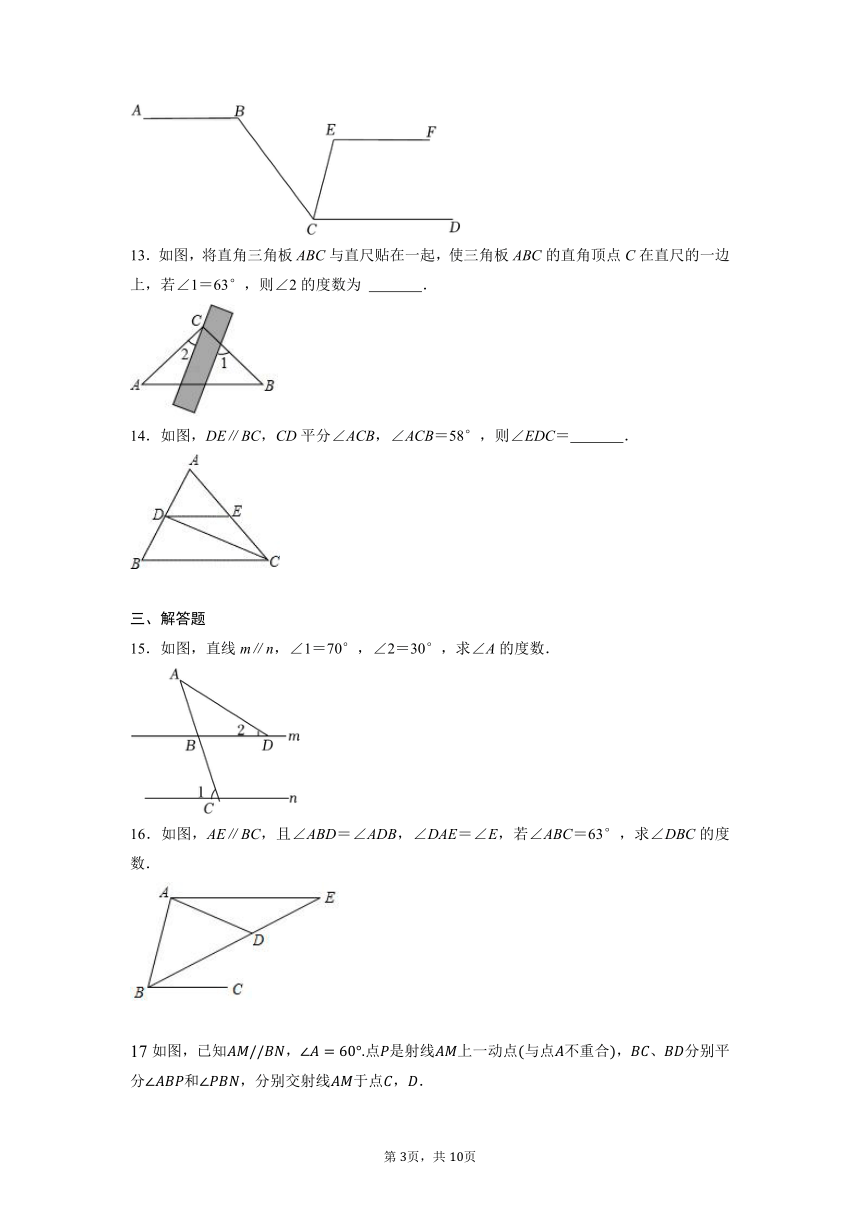
1.如图,若l1∥l2,l3∥l4,若∠1=110°,则∠2的度数为( )
A.70° B.80° C.90° D.110°
2.如图,AF是∠BAC的平分线,DF∥AC,若∠1=25°,则∠BDF的度数为( )
A.25° B.50° C.75° D.100°
3.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=25°,则∠2的度数是( )
A.55° B.60° C.65° D.70°
4.直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;(2)如果a∥b,b∥c,c∥d,那么a∥d;(3)如果a∥b,b⊥c,那么a⊥c;(4)如果a与b相交,b与c相交,那么a与c相交.在上述四种说法中,正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
5.一个学员在广场上驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
A. 第一次向右拐 50° ,第二次向左拐130° B. 第一次向右拐 50° ,第二次向右拐130°
C. 第一次向左拐 50° ,第二次向左拐130° D. 第一次向左拐 30° ,第二次向右拐 30°
6.如图,已知直线l1∥l2 , 将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于( )
A. 39° B. 45° C. 50° D. 51°
7如图,直线,,则的度数是
A.
B.
C.
D.
8.如果两个角的两边两两互相平行,且一个角的等于另一个角的,则这两个角的度数分别是( )
A.48°,72° B.72°,108°
C.48°,72°或72°,108° D.80°,120°
9.如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=24°,则∠EGF等于( )
A.24° B.78° C.66° D.56°
10.如图,AB∥CD,有图中α,β,γ三角之间的关系是( )
A.α+β+γ=180° B.α﹣β+γ=180° C.α+β﹣γ=180° D.α+β+γ=360°
二、填空题
11若两条平行线被第三条直线所截,则任意一组同位角的平分线互相 任意一组内错角的平分线互相 任意一组同旁内角的平分线互相 填“平行”或“垂直”.
12.如图,AB∥CD∥EF,若∠ABC=125°,∠CEF=105°,则∠BCE的度数为 .
13.如图,将直角三角板ABC与直尺贴在一起,使三角板ABC的直角顶点C在直尺的一边上,若∠1=63°,则∠2的度数为 .
14.如图,DE∥BC,CD平分∠ACB,∠ACB=58°,则∠EDC= .
三、解答题
15.如图,直线m∥n,∠1=70°,∠2=30°,求∠A的度数.
16.如图,AE∥BC,且∠ABD=∠ADB,∠DAE=∠E,若∠ABC=63°,求∠DBC的度数.
17如图,已知,点是射线上一动点与点不重合,、分别平分和,分别交射线于点,.
的度数是______;,______;
求的度数;
当点运动时,与之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
答案和解析
1.解:∵l1∥l2,∠1=110°,
∴∠1+∠3=180°.
∴∠3=70°.
∵l3∥l4,
∴∠2=∠3=70°.
故选:A.
2.解:∵DF∥AC,
∴∠FAC=∠1=25°,
∵AF是∠BAC的平分线,
∴∠BAF=∠FAC=25°,
∴∠BAC=50°,
∵DF∥AC,
∴∠BDF=∠BAC=50°
故选:B.
3.解:∵∠BEF是△AEF的外角,∠1=25°,∠F=30°,
∴∠BEF=∠1+∠F=55°,
∵AB∥CD,
∴∠2=∠BEF=55°.
故选:A.
4.【答案】 C
【考点】平行线的判定与性质
解:直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;正确.(2)如果a∥b,b∥c,c∥d,那么a∥d;正确.(3)如果a∥b,b⊥c,那么a⊥c;正确.(4)如果a与b相交,b与c相交,那么a与c相交.错误。所以正确的有3个,故选:C.
【分析】根据垂直于同一直线的两直线平行,平行公理对各小题分析判断即可得解.
5.【答案】 D
【考点】平行线的性质
解:∵两次拐弯后,按原来的相反方向前进,
∴两次拐弯的方向相同,形成的角是同位角,
故答案为:D.
【分析】根据平行线的性质分别判断得出即可.
6.【答案】 D
【考点】平行线的性质
解:作BD∥l1 , 如图所示:
∵BD∥l1 ,
∴∠1=∠CBD,
双∵l1∥l2 ,
∴BD∥l2 ,
∴∠ABD=∠2,
又∵∠1=39°,
∴∠CDB=39°
又∵∠CBA=∠CBD+∠ABD=90°,
∴∠ABD=51°,
∴∠2=51°.
故答案为:D.
【分析】由BD∥l1得∠1=∠CBD=39°,根据平行公理的推论得BD∥l2 , 其性质得∠ABD=∠2,角的和差求得∠2=51°.
7.【答案】
【解析】
解:如图:直线直线,,
,
.
故选B.
8.【答案】 C
【考点】平行线的性质
解:过C作CF∥AB,
∵AB∥DE,
∴AB∥CF∥DE,
∴∠1=∠α=40°,∠2=180°-∠β,
∵∠BCD=90°,
∴∠1+∠2=40°+180°-∠β=90°,
∴∠β=130°.
故答案为:C.
【分析】过C作CF∥AB,根据平行线的性质得到∠1=∠α=40°,∠2=180°-∠β,于是得到结论.
9.【答案】 C
【考点】垂线,平行线的性质
解:∵∠ACB=90°,
∴∠ABC+∠CAB=90°.
∵CE⊥AB,
∴∠CAB+∠ACE=90°.
∵AB∥CD,
∴∠DCB=∠ABC,
∴∠DCB+∠CAB=90°.
∴与∠CAB互余的角有∠ACE,∠ABC,∠DCB,共3个,
故答案为:C.
【分析】先由∠ACB=90°可得出∠ABC+∠CAB=90°,然后由CE⊥AB可得出∠CAB+∠ACE=90°,再由平行线的性质可知∠DCB=∠ABC,故∠DCB+∠CAB=90°,由此可得出结论.
10.【答案】 C
【考点】平行线的性质
解:解:作直线EF//AB
∵AB//CD、EF//AB
∴AB//CD//EF
∴ +∠1=180°, +∠2=180°
∵∠1+∠2=
∴
故答案为:C
【分析】本题考查平行线间的拐点问题,首先过拐点作平行线,再根据两直线平行,同旁内角互补即可得到答案.
11.【答案】平行
12.解:∵AB∥CD∥EF,∠ABC=125°,∠CEF=105°,
∴∠BCD=∠ABC=125°,∠DCE=180°﹣∠CEF=75°,
∴∠BCE=∠BCD﹣∠DCE=50°.
故答案为:50°.
13.解:∵直尺的两边平行,∠1=63°,
∴∠1=∠3=63°,
∵∠2+∠3=90°,
∴∠ACB=∠2=90°﹣∠3=90°﹣63°=27°,
故答案为:27°.
14.解:∵CD平分∠ACB,∠ACB=58°,
∴∠ECD=∠ACB=29°,
∵DE∥BC,
∴∠EDC=∠ECD=29°.
故答案为:29°.
15.解:∵m∥n,
∴∠3=∠1=70°,
∵∠3=∠2+∠A,
∴∠A=∠3﹣∠2
=70°﹣30°
=40°.
16.解:∵∠DAE=∠E,∠ADB是△ADE的外角,
∴∠ADB=∠DAE+∠E=2∠E,
∵∠ABD=∠ADB,
∴∠ABD=2∠E,
∵AE∥BC,
∴∠E=∠DBC,
∴∠ABD=2∠DBC,
∵∠ABC=63°,
∴∠ABD+∠DBC=63°,
即2∠DBC+∠DBC=63°,
解得:∠DBC=21°.
故∠DBC的度数为21°.
【答案】
【解析】解:,,
,
;
,
,
故答案为:,;
,
,
,
,
平分,平分,
,,
,
;
不变,::.
,
,,
平分,
,
::.
由平行线的性质:两直线平行同旁内角互补和内错角相等可得;
由知,再根据角平分线的定义知、,可得,即;
由得、,根据平分知,
从而可得:第10页,共10页
第11页,共1页
一、选择题
1.如图,若l1∥l2,l3∥l4,若∠1=110°,则∠2的度数为( )
A.70° B.80° C.90° D.110°
2.如图,AF是∠BAC的平分线,DF∥AC,若∠1=25°,则∠BDF的度数为( )
A.25° B.50° C.75° D.100°
3.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=25°,则∠2的度数是( )
A.55° B.60° C.65° D.70°
4.直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;(2)如果a∥b,b∥c,c∥d,那么a∥d;(3)如果a∥b,b⊥c,那么a⊥c;(4)如果a与b相交,b与c相交,那么a与c相交.在上述四种说法中,正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
5.一个学员在广场上驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
A. 第一次向右拐 50° ,第二次向左拐130° B. 第一次向右拐 50° ,第二次向右拐130°
C. 第一次向左拐 50° ,第二次向左拐130° D. 第一次向左拐 30° ,第二次向右拐 30°
6.如图,已知直线l1∥l2 , 将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于( )
A. 39° B. 45° C. 50° D. 51°
7如图,直线,,则的度数是
A.
B.
C.
D.
8.如果两个角的两边两两互相平行,且一个角的等于另一个角的,则这两个角的度数分别是( )
A.48°,72° B.72°,108°
C.48°,72°或72°,108° D.80°,120°
9.如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=24°,则∠EGF等于( )
A.24° B.78° C.66° D.56°
10.如图,AB∥CD,有图中α,β,γ三角之间的关系是( )
A.α+β+γ=180° B.α﹣β+γ=180° C.α+β﹣γ=180° D.α+β+γ=360°
二、填空题
11若两条平行线被第三条直线所截,则任意一组同位角的平分线互相 任意一组内错角的平分线互相 任意一组同旁内角的平分线互相 填“平行”或“垂直”.
12.如图,AB∥CD∥EF,若∠ABC=125°,∠CEF=105°,则∠BCE的度数为 .
13.如图,将直角三角板ABC与直尺贴在一起,使三角板ABC的直角顶点C在直尺的一边上,若∠1=63°,则∠2的度数为 .
14.如图,DE∥BC,CD平分∠ACB,∠ACB=58°,则∠EDC= .
三、解答题
15.如图,直线m∥n,∠1=70°,∠2=30°,求∠A的度数.
16.如图,AE∥BC,且∠ABD=∠ADB,∠DAE=∠E,若∠ABC=63°,求∠DBC的度数.
17如图,已知,点是射线上一动点与点不重合,、分别平分和,分别交射线于点,.
的度数是______;,______;
求的度数;
当点运动时,与之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
答案和解析
1.解:∵l1∥l2,∠1=110°,
∴∠1+∠3=180°.
∴∠3=70°.
∵l3∥l4,
∴∠2=∠3=70°.
故选:A.
2.解:∵DF∥AC,
∴∠FAC=∠1=25°,
∵AF是∠BAC的平分线,
∴∠BAF=∠FAC=25°,
∴∠BAC=50°,
∵DF∥AC,
∴∠BDF=∠BAC=50°
故选:B.
3.解:∵∠BEF是△AEF的外角,∠1=25°,∠F=30°,
∴∠BEF=∠1+∠F=55°,
∵AB∥CD,
∴∠2=∠BEF=55°.
故选:A.
4.【答案】 C
【考点】平行线的判定与性质
解:直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;正确.(2)如果a∥b,b∥c,c∥d,那么a∥d;正确.(3)如果a∥b,b⊥c,那么a⊥c;正确.(4)如果a与b相交,b与c相交,那么a与c相交.错误。所以正确的有3个,故选:C.
【分析】根据垂直于同一直线的两直线平行,平行公理对各小题分析判断即可得解.
5.【答案】 D
【考点】平行线的性质
解:∵两次拐弯后,按原来的相反方向前进,
∴两次拐弯的方向相同,形成的角是同位角,
故答案为:D.
【分析】根据平行线的性质分别判断得出即可.
6.【答案】 D
【考点】平行线的性质
解:作BD∥l1 , 如图所示:
∵BD∥l1 ,
∴∠1=∠CBD,
双∵l1∥l2 ,
∴BD∥l2 ,
∴∠ABD=∠2,
又∵∠1=39°,
∴∠CDB=39°
又∵∠CBA=∠CBD+∠ABD=90°,
∴∠ABD=51°,
∴∠2=51°.
故答案为:D.
【分析】由BD∥l1得∠1=∠CBD=39°,根据平行公理的推论得BD∥l2 , 其性质得∠ABD=∠2,角的和差求得∠2=51°.
7.【答案】
【解析】
解:如图:直线直线,,
,
.
故选B.
8.【答案】 C
【考点】平行线的性质
解:过C作CF∥AB,
∵AB∥DE,
∴AB∥CF∥DE,
∴∠1=∠α=40°,∠2=180°-∠β,
∵∠BCD=90°,
∴∠1+∠2=40°+180°-∠β=90°,
∴∠β=130°.
故答案为:C.
【分析】过C作CF∥AB,根据平行线的性质得到∠1=∠α=40°,∠2=180°-∠β,于是得到结论.
9.【答案】 C
【考点】垂线,平行线的性质
解:∵∠ACB=90°,
∴∠ABC+∠CAB=90°.
∵CE⊥AB,
∴∠CAB+∠ACE=90°.
∵AB∥CD,
∴∠DCB=∠ABC,
∴∠DCB+∠CAB=90°.
∴与∠CAB互余的角有∠ACE,∠ABC,∠DCB,共3个,
故答案为:C.
【分析】先由∠ACB=90°可得出∠ABC+∠CAB=90°,然后由CE⊥AB可得出∠CAB+∠ACE=90°,再由平行线的性质可知∠DCB=∠ABC,故∠DCB+∠CAB=90°,由此可得出结论.
10.【答案】 C
【考点】平行线的性质
解:解:作直线EF//AB
∵AB//CD、EF//AB
∴AB//CD//EF
∴ +∠1=180°, +∠2=180°
∵∠1+∠2=
∴
故答案为:C
【分析】本题考查平行线间的拐点问题,首先过拐点作平行线,再根据两直线平行,同旁内角互补即可得到答案.
11.【答案】平行
12.解:∵AB∥CD∥EF,∠ABC=125°,∠CEF=105°,
∴∠BCD=∠ABC=125°,∠DCE=180°﹣∠CEF=75°,
∴∠BCE=∠BCD﹣∠DCE=50°.
故答案为:50°.
13.解:∵直尺的两边平行,∠1=63°,
∴∠1=∠3=63°,
∵∠2+∠3=90°,
∴∠ACB=∠2=90°﹣∠3=90°﹣63°=27°,
故答案为:27°.
14.解:∵CD平分∠ACB,∠ACB=58°,
∴∠ECD=∠ACB=29°,
∵DE∥BC,
∴∠EDC=∠ECD=29°.
故答案为:29°.
15.解:∵m∥n,
∴∠3=∠1=70°,
∵∠3=∠2+∠A,
∴∠A=∠3﹣∠2
=70°﹣30°
=40°.
16.解:∵∠DAE=∠E,∠ADB是△ADE的外角,
∴∠ADB=∠DAE+∠E=2∠E,
∵∠ABD=∠ADB,
∴∠ABD=2∠E,
∵AE∥BC,
∴∠E=∠DBC,
∴∠ABD=2∠DBC,
∵∠ABC=63°,
∴∠ABD+∠DBC=63°,
即2∠DBC+∠DBC=63°,
解得:∠DBC=21°.
故∠DBC的度数为21°.
【答案】
【解析】解:,,
,
;
,
,
故答案为:,;
,
,
,
,
平分,平分,
,,
,
;
不变,::.
,
,,
平分,
,
::.
由平行线的性质:两直线平行同旁内角互补和内错角相等可得;
由知,再根据角平分线的定义知、,可得,即;
由得、,根据平分知,
从而可得:第10页,共10页
第11页,共1页
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
