2021-2022学年苏科版九年级数学下册5.5用二次函数解决问题专项训练(一)(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册5.5用二次函数解决问题专项训练(一)(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 214.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 19:35:50 | ||
图片预览




文档简介
【用二次函数解决问题】专项提升训练(一)
一.选择题
1.据省统计局公布的数据,安徽省2019年第二季度GDP总值约为7.9千亿元人民币,若我省第四季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=7.9(1+2x)
B.y=7.9(1﹣x)2
C.y=7.9(1+x)2
D.y=7.9+7.9(1+x)+7.9(1+x)2
2. 从地面竖直向上抛出一个小球,小球的上升高度(单位:)与小球运动时间(单位:)之间的关系式为,那么,小球从抛出至回落到地面所需的时间是( )
A. B. C. D.
3. 心理学家发现:学生对概念的接受能力与提出概念的时间之间是二次函数关系,当提出概念时,学生对概念的接受力最大,为;当提出概念时,学生对概念的接受能力就剩下,则与满足的二次函数关系式为( )
A. B.
C. D.
4. 如图,在平面直角坐标系中,抛物线与轴交于、两点,点在轴的负半轴,点在轴的正半轴,与轴交于点,且,,.则下列判断中正确的是( )
A.此抛物线的解析式为
B.当时,随着的增大而增大
C.此抛物线与直线只有一个交点
D.在此抛物线上的某点,使的面积等于,这样的点共有三个
5.今年由于受新型冠状病毒的影响,一次性医用口罩的销量剧增.某药店一月份销售量是5000枚,二、三两个月销售量连续增长.若月平均增长率为x,则该药店三月份销售口罩枚数y(枚)与x的函数关系式是( )
A.y=5000(1+x) B.y=5000(1+x)2
C.y=5000(1+x2) D.y=5000(1+2x)
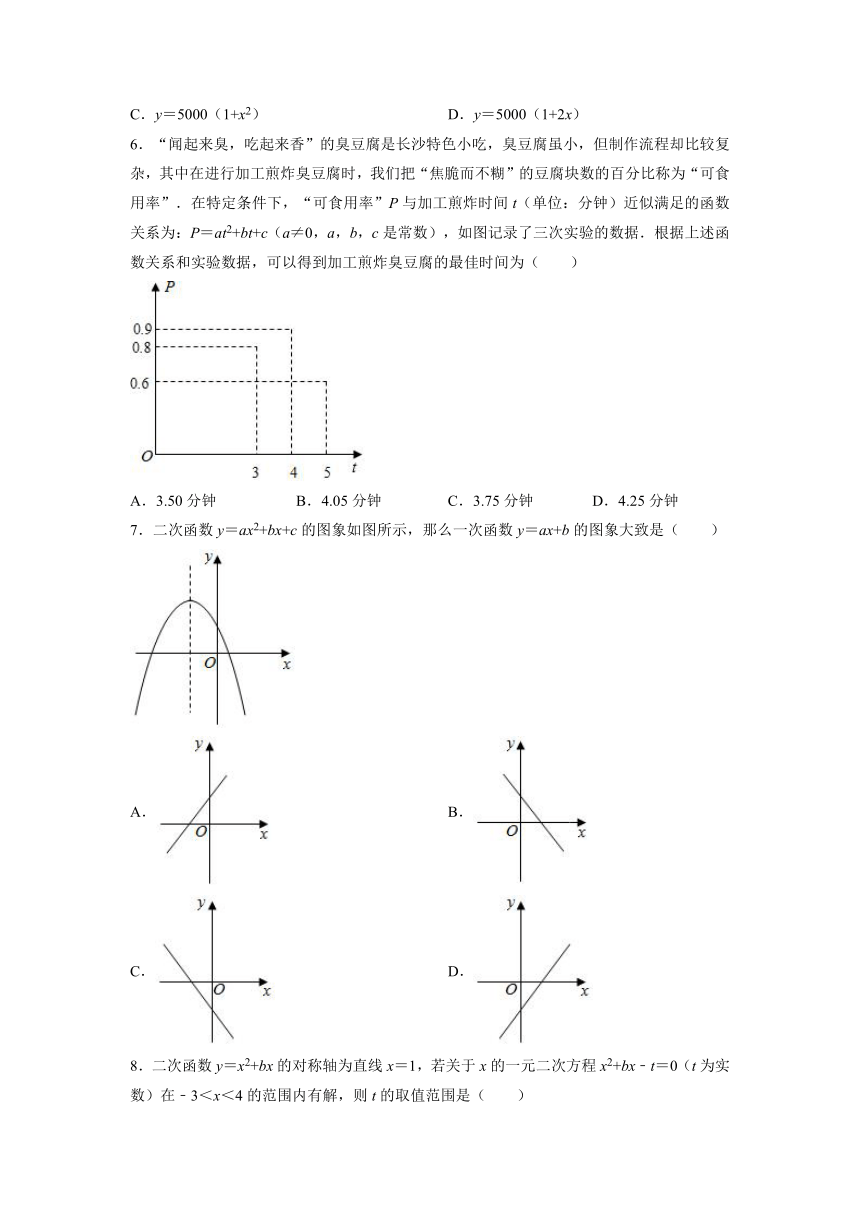
6.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”P与加工煎炸时间t(单位:分钟)近似满足的函数关系为:P=at2+bt+c(a≠0,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟 B.4.05分钟 C.3.75分钟 D.4.25分钟
7.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
A. B.
C. D.
8.二次函数y=x2+bx的对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣3<x<4的范围内有解,则t的取值范围是( )
A.0<t<8 B.﹣1≤t<15 C.﹣1≤t<8 D.8<t<15
9.在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则( )
A.M=N﹣1或M=N+1 B.M=N﹣1或M=N+2
C.M=N或M=N+1 D.M=N或M=N﹣1
10.烟花厂为成都春节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.6s
二.填空题
11.一位运动员投掷铅球,如果铅球运行时离地面的高度为y(米)关于水平距离x(米)的函数解析式为,那么该运动员的铅球投掷成绩为 米.
12.把一个小球以20米/秒的速度竖直向上弹出,它在空中的高度h(米)与时间t(秒),满足关系:h=20t-5t2 , 当小球达到最高点时,小球的运动时间为第________秒时.
13.如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪AB所在直线的距离为2m,且到地面的距离为3m,则水流的落地点C到水枪底部B的距离为________.
某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为________.
15.在一定条件下,若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+2t,则当物体经过的路程是88米时,该物体所经过的时间为 秒.
三.解答题
16.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.
(1)求这条抛物线的解析式;
(2)求运动员落水点与点C的距离.
17.某单位为响应市“创建全国文明城市”的号召,不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并求出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)当矩形ABCD空地的面积最大时,利用的墙长是多少m;并求此时的最大面积.
18.某汽车清洗店,清洗一辆汽车定价20元时每天能清洗45辆,定价25元时每天能清洗30辆,假设清洗汽车辆数y(辆)与定价x(元)(x取整数)是一次函数关系(清洗每辆汽车成本忽略不计).
(1)求y与x之间的函数表达式;
(2)若清洗一辆汽车定价不低于15元且不超过50元,且该汽车清洗店每天需支付电费、水和员工工资共计200元,问:定价为多少时,该汽车清洗店每天获利最大?最大获利多少?
19.如图,以D为顶点的抛物线y=ax2+2x+c交x轴于点A,B(6,0),交y轴于点C(0,6).
(1)求抛物线的解析式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
20.已知直线l1:y=﹣2x+10交y轴于点A,交x轴于点B,二次函数的图象过A,B两点,交x轴于另一点C,BC=4,且对于该二次函数图象上的任意两点P1(x1,y1),P2(x2,y2),当x1>x2≥5时,总有y1>y2.
(1)求二次函数的表达式;
(2)若直线l2:y=mx+n(n≠10),求证:当m=﹣2时,l2∥l1;
(3)E为线段BC上不与端点重合的点,直线l3:y=﹣2x+q过点C且交直线AE于点F,求△ABE与△CEF面积之和的最小值.
参考答案
一.选择题
1.解:设平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是:y=7.9(1+x)2.
故选:C.
2.
【答案】
A
【解答】
解:由题意可得:时,,
解得:,,
故小球从抛出至回落到地面所需的时间是:秒.
故选:.
3.
【答案】
D
【解答】
解:设抛物线解析式为:,
将代入得:
,
解得:,
故:.
故选:.
4.
【答案】
C
【解答】
解:∵ ,而,,
∴ ,,即,,,
∴ 二次函数的解析式为,故错误.
∵ 二次函数的对称轴为,
∴ 当时,随着的增大而先减小再增大,故错误.
∵ 此二次函数的最小值为,
∴ 此抛物线与直线只有一个交点,正确.
∵ 要使的面积等于,须使到轴的距离为,这样的点共有个,故错误.
故选:.
5.解:该药店三月份销售口罩枚数y(枚)与x的函数关系式是:y=5000(1+x)2.
故选:B.
6.解:将图象中的三个点(3,0.8)、(4,0.9)、(5,0.6)代入函数关系P=at2+bt+c中,
,
解得,
所以函数关系式为:P=﹣0.2t2+1.5t﹣1.9,
由题意可知:加工煎炸臭豆腐的最佳时间为抛物线顶点的横坐标:
t=﹣=﹣=3.75,
则当t=3.75分钟时,可以得到最佳时间.
故选:C.
7.解:∵y=ax2+bx+c的图象的开口向下,
∴a<0,
∵对称轴在y轴的左侧,
∴b<0,
∴一次函数y=ax+b的图象经过二,三,四象限.
故选:C.
8.解:∵抛物线y=x2+bx的对称轴为直线x=1,
∴﹣=1,解得b=﹣2,
关于x的一元二次方程x2+bx﹣t=0变形为x2﹣2x﹣t=0,
把关于x的一元二次方程x2﹣2x﹣t=0(t为实数)在﹣3<x<4的范围内有实数根转化为抛物线y=x2﹣2x﹣t(t为实数)在﹣3<x<4的范围与x轴有交点(如图),
∴△=(﹣2)2﹣4(﹣t)≥0且x=﹣3时,y>0,即9+6﹣t>0,
解得﹣1≤t<15.
故选:B.
9.解:∵y=(x+a)(x+b),a≠b,
∴函数y=(x+a)(x+b)的图象与x轴有2个交点,
∴M=2,
∵函数y=(ax+1)(bx+1)=abx2+(a+b)x+1,
∴当ab≠0时,△=(a+b)2﹣4ab=(a﹣b)2>0,函数y=(ax+1)(bx+1)的图象与x轴有2个交点,即N=2,此时M=N;
当ab=0时,不妨令a=0,∵a≠b,∴b≠0,函数y=(ax+1)(bx+1)=bx+1为一次函数,与x轴有一个交点,即N=1,此时M=N+1;
综上可知,M=N或M=N+1.
故选:C.
另一解法:∵a≠b,
∴抛物线y=(x+a)(x+b)与x轴有两个交点,
∴M=2,
又∵函数y=(ax+1)(bx+1)的图象与x轴有N个交点,
而y=(ax+1)(bx+1)=abx2+(a+b)x+1,它至多是一个二次函数,至多与x轴有两个交点,
∴N≤2,
∴N≤M,
∴不可能有M=N﹣1,
故排除A、B、D,
故选:C.
10.解:∵礼炮在点火升空到最高点引爆,
∴t=﹣==6(s),
故选:D.
二.填空题
11.解:令=0,
解得x=10或﹣2(舍去﹣2),
故答案为10.
12.【答案】 2
【考点】二次函数的实际应用-抛球问题
解:h=20t-5t2=-5(t-2)2+20,
∵-5<0,∴函数有最大值,
则当t=2时,球的高度最高.
故答案为2.
【分析】根据二次函数的性质解答即可.
13.【答案】
【考点】二次函数的实际应用-喷水问题
解:如图,
∵喷水口A距地面2m,
∴点A(0,2),
∵如果水流的最高点P到喷水枪AB所在直线的距离为2m,且到地面的距离为3m,
∴抛物线的顶点坐标为(2,3),
设抛物线的解析式为:y=a(x-2)2+3.
∴4a+3=2
解之:a=-
∴
当y=0时,
解之:x=(取正值).
故答案为:.
【分析】以点B为坐标原点建立平面直角坐标系,可得到点A,P的坐标,利用待定系数法求出抛物线的解析式;再求出当y=0时的x的值,根据点C的坐标,可得到点C到点B的距离。
14.【答案】0<a≤5
【考点】二次函数的实际应用-销售问题
解:设未来30天每天获得的利润为y,
y=(110-40-t)(20+4t)﹣(20+4t)a
化简,得
y=﹣4t2+(260-4a)t+1400﹣20a
每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,
∴ ≥﹣4×302+×30+1400﹣20a
解得,a≤5,
又∵a>0,
即a的取值范围是:0<a≤5
【分析】设未来30天每天获得的利润为y,则每天销售的数量为:(20+4t)件,每件的利润为(110-40-t)元,销售商品所获得的利润为(110-40-t)(20+4t)元,需要缴纳电商平台推广费(20+4t)a元,根据每天实际获得的利润等于销售商品获得的利润减去需要缴纳电商平台推广费列出函数关系式,根据题意列出不等式,求解得出a的取值范围。
15.解:把s=88代入s=5t2+2t得:
5t2+2t=88.
解得t1=4,t2=﹣4.4(舍去),
即t=4秒.
故答案为:4.
三.解答题
16.解:(1)如图所示,建立平面直角坐标系,
由题意可得抛物线的顶点坐标为(3,4),点A坐标为(2,3),
设抛物线的解析式为y=a(x﹣3)2+4,
将点A坐标(2,3)代入得:3=a(2﹣3)2+4,
解得:a=﹣1,
∴这条抛物线的解析式为y=﹣(x﹣3)2+4;
(2)∵y=﹣(x﹣3)2+4,
∴令y=0得:0=﹣(x﹣3)2+4,
解得:x1=1,x2=5,
∵起跳点A坐标为(2,3),
∴x1=1,不符合题意,
∴x=5,
∴运动员落水点与点C的距离为5米.
17.解:(1)y=x(36﹣2x)
=﹣2x2+36x,
∵0<36﹣2x≤18,
∴9≤x<18.
∴y与x之间的函数关系式为y=﹣2x2+36x(9≤x<18);
(2)由题意得:﹣2x2+36x=160m2,
解得x1=8,x2=10,
∵9≤x<18,
∴x1=8不符合题意,
∴x=10;
(3)∵y=﹣2x2+36x
=﹣2(x﹣9)2+162,
∴当x=9时,y有最大值162.
∴墙长36﹣2x=36﹣18=18(m),
∴矩形ABCD空地的面积最大为162m2时,利用的墙长是18m.
18.解:(1)设y与x的一次函数式为y=kx+b,由题意可知:
,解得:,
∴y与x之间的函数表达式为y=﹣3x+105;
(2)设汽车美容店每天获利润为w元,由题意得:
w=xy﹣200
=x(﹣3x+105)﹣200
=﹣3(x﹣17.5)2﹣718.75,
∵15≤x≤50,且x为整数,
∴当x=17或18时,w最大=718(元).
∴定价为17元或18元时,该汽车清洗店每天获利最大,最大获利是718元.
19.解:(1)将B(6,0),C(0,6)代入y=ax2+2x+c,得:,
解得:,
∴抛物线的解析式为y=﹣x2+2x+6.
(2)当y=0时,﹣x2+2x+6=0,
解得:x1=﹣2,x2=6,
∴点A的坐标为(﹣2,0).
∵点B的坐标为(6,0),点C的坐标为(0,6),
∴直线BC的解析式为y=﹣x+6.
如图1,作O关于BC的对称点O′,则点O′的坐标为(6,6).
∵O与O′关于直线BC对称,
∴PO=PO′,
∴PO+PA的最小值=PO′+PA=AO′═=10.
设直线AO′的解析式为y=kx+m,
将A(﹣2,0),Q′(6,6)代入y=kx+m,得:,
解得:,
∴直线AO′的解析式为y=x+.
联立直线AO′和直线BC的解析式成方程组,得:,
解得:,
∴点P的坐标为(,).
(3)∵y=﹣x2+2x+6=﹣(x﹣2)2+8,
∴点D的坐标为(2,8).
又∵点C的坐标为(0,6),点B的坐标为(6,0),
∴CD==2,BC═=6,BD═=4,
∴CD2+BC2=BD2,
∴∠BCD=90°.
∵点A的坐标(﹣2,0),点C的坐标为(0,6),
∴OA=2,OC=6,
∴==2,.
又∵∠AOC=∠DCB=90°,
∴△AOC∽△DCB,
∴当Q的坐标为(0,0)时,△AQC∽△DCB.
如图2,连接AC,过点C作CQ⊥AC,交x轴于点Q.
∵△ACQ为直角三角形,CO⊥AQ,
∴△ACQ∽△AOC.
又∵△AOC∽△DCB,
∴△ACQ∽DCB,
∴,即,
∴AQ=20,
∴点Q的坐标为(18,0).
综上所述:当Q的坐标为(0,0)或(18,0)时,以A,C,Q为顶点的三角形与△BCD相似.
20.解:(1)∵直线l1:y=﹣2x+10交y轴于点A,交x轴于点B,
∴点A(0,10),点B(5,0),
∵BC=4,
∴点C(9,0)或点C(1,0),
∵点P1(x1,y1),P2(x2,y2),当x1>x2≥5时,总有y1>y2.
∴当x≥5时,y随x的增大而增大,
当抛物线过点C(9,0)时,则当5<x<7时,y随x的增大而减少,不合题意舍去,
当抛物线过点C(1,0)时,则当x>3时,y随x的增大而增大,符合题意,
∴设抛物线解析式为:y=a(x﹣1)(x﹣5),过点A(0,10),
∴10=5a,
∴a=2,
∴抛物线解析式为:y=2(x﹣1)(x﹣5)=2x2﹣12x+10;
方法二:设抛物线解析式为y=ax2+bx+c,
由题意可得:,
解得:,
∴抛物线解析式为:y=2x2﹣12x+10;
(2)当m=﹣2时,直线l2:y=﹣2x+n(n≠10),
∴直线l2:y=﹣2x+n(n≠10)与直线l1:y=﹣2x+10不重合,
假设l1与l2不平行,则l1与l2必相交,设交点为P(xP,yP),
∴
解得:n=10,
∵n=10与已知n≠10矛盾,
∴l1与l2不相交,
∴l2∥l1;
(3)如图,
、
∵直线l3:y=﹣2x+q过点C,
∴0=﹣2×1+q,
∴q=2,
∴直线l3解析式为:y=﹣2x+2,
∴l3∥l1,
∴CF∥AB,
∴∠ECF=∠ABE,∠CFE=∠BAE,
∴△CEF∽△BEA,
∴=()2,
设BE=t(0<t<4),则CE=4﹣t,
∴S△ABE=×t×10=5t,
∴S△CEF=()2×S△ABE=()2×5t=,
∴S△ABE+S△CEF=5t+=10t+﹣40=10(﹣)2+40﹣40,
∴当t=2时,S△ABE+S△CEF的最小值为40﹣40.
一.选择题
1.据省统计局公布的数据,安徽省2019年第二季度GDP总值约为7.9千亿元人民币,若我省第四季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=7.9(1+2x)
B.y=7.9(1﹣x)2
C.y=7.9(1+x)2
D.y=7.9+7.9(1+x)+7.9(1+x)2
2. 从地面竖直向上抛出一个小球,小球的上升高度(单位:)与小球运动时间(单位:)之间的关系式为,那么,小球从抛出至回落到地面所需的时间是( )
A. B. C. D.
3. 心理学家发现:学生对概念的接受能力与提出概念的时间之间是二次函数关系,当提出概念时,学生对概念的接受力最大,为;当提出概念时,学生对概念的接受能力就剩下,则与满足的二次函数关系式为( )
A. B.
C. D.
4. 如图,在平面直角坐标系中,抛物线与轴交于、两点,点在轴的负半轴,点在轴的正半轴,与轴交于点,且,,.则下列判断中正确的是( )
A.此抛物线的解析式为
B.当时,随着的增大而增大
C.此抛物线与直线只有一个交点
D.在此抛物线上的某点,使的面积等于,这样的点共有三个
5.今年由于受新型冠状病毒的影响,一次性医用口罩的销量剧增.某药店一月份销售量是5000枚,二、三两个月销售量连续增长.若月平均增长率为x,则该药店三月份销售口罩枚数y(枚)与x的函数关系式是( )
A.y=5000(1+x) B.y=5000(1+x)2
C.y=5000(1+x2) D.y=5000(1+2x)
6.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”P与加工煎炸时间t(单位:分钟)近似满足的函数关系为:P=at2+bt+c(a≠0,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟 B.4.05分钟 C.3.75分钟 D.4.25分钟
7.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
A. B.
C. D.
8.二次函数y=x2+bx的对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣3<x<4的范围内有解,则t的取值范围是( )
A.0<t<8 B.﹣1≤t<15 C.﹣1≤t<8 D.8<t<15
9.在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则( )
A.M=N﹣1或M=N+1 B.M=N﹣1或M=N+2
C.M=N或M=N+1 D.M=N或M=N﹣1
10.烟花厂为成都春节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.6s
二.填空题
11.一位运动员投掷铅球,如果铅球运行时离地面的高度为y(米)关于水平距离x(米)的函数解析式为,那么该运动员的铅球投掷成绩为 米.
12.把一个小球以20米/秒的速度竖直向上弹出,它在空中的高度h(米)与时间t(秒),满足关系:h=20t-5t2 , 当小球达到最高点时,小球的运动时间为第________秒时.
13.如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪AB所在直线的距离为2m,且到地面的距离为3m,则水流的落地点C到水枪底部B的距离为________.
某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为________.
15.在一定条件下,若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+2t,则当物体经过的路程是88米时,该物体所经过的时间为 秒.
三.解答题
16.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.
(1)求这条抛物线的解析式;
(2)求运动员落水点与点C的距离.
17.某单位为响应市“创建全国文明城市”的号召,不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并求出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)当矩形ABCD空地的面积最大时,利用的墙长是多少m;并求此时的最大面积.
18.某汽车清洗店,清洗一辆汽车定价20元时每天能清洗45辆,定价25元时每天能清洗30辆,假设清洗汽车辆数y(辆)与定价x(元)(x取整数)是一次函数关系(清洗每辆汽车成本忽略不计).
(1)求y与x之间的函数表达式;
(2)若清洗一辆汽车定价不低于15元且不超过50元,且该汽车清洗店每天需支付电费、水和员工工资共计200元,问:定价为多少时,该汽车清洗店每天获利最大?最大获利多少?
19.如图,以D为顶点的抛物线y=ax2+2x+c交x轴于点A,B(6,0),交y轴于点C(0,6).
(1)求抛物线的解析式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
20.已知直线l1:y=﹣2x+10交y轴于点A,交x轴于点B,二次函数的图象过A,B两点,交x轴于另一点C,BC=4,且对于该二次函数图象上的任意两点P1(x1,y1),P2(x2,y2),当x1>x2≥5时,总有y1>y2.
(1)求二次函数的表达式;
(2)若直线l2:y=mx+n(n≠10),求证:当m=﹣2时,l2∥l1;
(3)E为线段BC上不与端点重合的点,直线l3:y=﹣2x+q过点C且交直线AE于点F,求△ABE与△CEF面积之和的最小值.
参考答案
一.选择题
1.解:设平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是:y=7.9(1+x)2.
故选:C.
2.
【答案】
A
【解答】
解:由题意可得:时,,
解得:,,
故小球从抛出至回落到地面所需的时间是:秒.
故选:.
3.
【答案】
D
【解答】
解:设抛物线解析式为:,
将代入得:
,
解得:,
故:.
故选:.
4.
【答案】
C
【解答】
解:∵ ,而,,
∴ ,,即,,,
∴ 二次函数的解析式为,故错误.
∵ 二次函数的对称轴为,
∴ 当时,随着的增大而先减小再增大,故错误.
∵ 此二次函数的最小值为,
∴ 此抛物线与直线只有一个交点,正确.
∵ 要使的面积等于,须使到轴的距离为,这样的点共有个,故错误.
故选:.
5.解:该药店三月份销售口罩枚数y(枚)与x的函数关系式是:y=5000(1+x)2.
故选:B.
6.解:将图象中的三个点(3,0.8)、(4,0.9)、(5,0.6)代入函数关系P=at2+bt+c中,
,
解得,
所以函数关系式为:P=﹣0.2t2+1.5t﹣1.9,
由题意可知:加工煎炸臭豆腐的最佳时间为抛物线顶点的横坐标:
t=﹣=﹣=3.75,
则当t=3.75分钟时,可以得到最佳时间.
故选:C.
7.解:∵y=ax2+bx+c的图象的开口向下,
∴a<0,
∵对称轴在y轴的左侧,
∴b<0,
∴一次函数y=ax+b的图象经过二,三,四象限.
故选:C.
8.解:∵抛物线y=x2+bx的对称轴为直线x=1,
∴﹣=1,解得b=﹣2,
关于x的一元二次方程x2+bx﹣t=0变形为x2﹣2x﹣t=0,
把关于x的一元二次方程x2﹣2x﹣t=0(t为实数)在﹣3<x<4的范围内有实数根转化为抛物线y=x2﹣2x﹣t(t为实数)在﹣3<x<4的范围与x轴有交点(如图),
∴△=(﹣2)2﹣4(﹣t)≥0且x=﹣3时,y>0,即9+6﹣t>0,
解得﹣1≤t<15.
故选:B.
9.解:∵y=(x+a)(x+b),a≠b,
∴函数y=(x+a)(x+b)的图象与x轴有2个交点,
∴M=2,
∵函数y=(ax+1)(bx+1)=abx2+(a+b)x+1,
∴当ab≠0时,△=(a+b)2﹣4ab=(a﹣b)2>0,函数y=(ax+1)(bx+1)的图象与x轴有2个交点,即N=2,此时M=N;
当ab=0时,不妨令a=0,∵a≠b,∴b≠0,函数y=(ax+1)(bx+1)=bx+1为一次函数,与x轴有一个交点,即N=1,此时M=N+1;
综上可知,M=N或M=N+1.
故选:C.
另一解法:∵a≠b,
∴抛物线y=(x+a)(x+b)与x轴有两个交点,
∴M=2,
又∵函数y=(ax+1)(bx+1)的图象与x轴有N个交点,
而y=(ax+1)(bx+1)=abx2+(a+b)x+1,它至多是一个二次函数,至多与x轴有两个交点,
∴N≤2,
∴N≤M,
∴不可能有M=N﹣1,
故排除A、B、D,
故选:C.
10.解:∵礼炮在点火升空到最高点引爆,
∴t=﹣==6(s),
故选:D.
二.填空题
11.解:令=0,
解得x=10或﹣2(舍去﹣2),
故答案为10.
12.【答案】 2
【考点】二次函数的实际应用-抛球问题
解:h=20t-5t2=-5(t-2)2+20,
∵-5<0,∴函数有最大值,
则当t=2时,球的高度最高.
故答案为2.
【分析】根据二次函数的性质解答即可.
13.【答案】
【考点】二次函数的实际应用-喷水问题
解:如图,
∵喷水口A距地面2m,
∴点A(0,2),
∵如果水流的最高点P到喷水枪AB所在直线的距离为2m,且到地面的距离为3m,
∴抛物线的顶点坐标为(2,3),
设抛物线的解析式为:y=a(x-2)2+3.
∴4a+3=2
解之:a=-
∴
当y=0时,
解之:x=(取正值).
故答案为:.
【分析】以点B为坐标原点建立平面直角坐标系,可得到点A,P的坐标,利用待定系数法求出抛物线的解析式;再求出当y=0时的x的值,根据点C的坐标,可得到点C到点B的距离。
14.【答案】0<a≤5
【考点】二次函数的实际应用-销售问题
解:设未来30天每天获得的利润为y,
y=(110-40-t)(20+4t)﹣(20+4t)a
化简,得
y=﹣4t2+(260-4a)t+1400﹣20a
每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,
∴ ≥﹣4×302+×30+1400﹣20a
解得,a≤5,
又∵a>0,
即a的取值范围是:0<a≤5
【分析】设未来30天每天获得的利润为y,则每天销售的数量为:(20+4t)件,每件的利润为(110-40-t)元,销售商品所获得的利润为(110-40-t)(20+4t)元,需要缴纳电商平台推广费(20+4t)a元,根据每天实际获得的利润等于销售商品获得的利润减去需要缴纳电商平台推广费列出函数关系式,根据题意列出不等式,求解得出a的取值范围。
15.解:把s=88代入s=5t2+2t得:
5t2+2t=88.
解得t1=4,t2=﹣4.4(舍去),
即t=4秒.
故答案为:4.
三.解答题
16.解:(1)如图所示,建立平面直角坐标系,
由题意可得抛物线的顶点坐标为(3,4),点A坐标为(2,3),
设抛物线的解析式为y=a(x﹣3)2+4,
将点A坐标(2,3)代入得:3=a(2﹣3)2+4,
解得:a=﹣1,
∴这条抛物线的解析式为y=﹣(x﹣3)2+4;
(2)∵y=﹣(x﹣3)2+4,
∴令y=0得:0=﹣(x﹣3)2+4,
解得:x1=1,x2=5,
∵起跳点A坐标为(2,3),
∴x1=1,不符合题意,
∴x=5,
∴运动员落水点与点C的距离为5米.
17.解:(1)y=x(36﹣2x)
=﹣2x2+36x,
∵0<36﹣2x≤18,
∴9≤x<18.
∴y与x之间的函数关系式为y=﹣2x2+36x(9≤x<18);
(2)由题意得:﹣2x2+36x=160m2,
解得x1=8,x2=10,
∵9≤x<18,
∴x1=8不符合题意,
∴x=10;
(3)∵y=﹣2x2+36x
=﹣2(x﹣9)2+162,
∴当x=9时,y有最大值162.
∴墙长36﹣2x=36﹣18=18(m),
∴矩形ABCD空地的面积最大为162m2时,利用的墙长是18m.
18.解:(1)设y与x的一次函数式为y=kx+b,由题意可知:
,解得:,
∴y与x之间的函数表达式为y=﹣3x+105;
(2)设汽车美容店每天获利润为w元,由题意得:
w=xy﹣200
=x(﹣3x+105)﹣200
=﹣3(x﹣17.5)2﹣718.75,
∵15≤x≤50,且x为整数,
∴当x=17或18时,w最大=718(元).
∴定价为17元或18元时,该汽车清洗店每天获利最大,最大获利是718元.
19.解:(1)将B(6,0),C(0,6)代入y=ax2+2x+c,得:,
解得:,
∴抛物线的解析式为y=﹣x2+2x+6.
(2)当y=0时,﹣x2+2x+6=0,
解得:x1=﹣2,x2=6,
∴点A的坐标为(﹣2,0).
∵点B的坐标为(6,0),点C的坐标为(0,6),
∴直线BC的解析式为y=﹣x+6.
如图1,作O关于BC的对称点O′,则点O′的坐标为(6,6).
∵O与O′关于直线BC对称,
∴PO=PO′,
∴PO+PA的最小值=PO′+PA=AO′═=10.
设直线AO′的解析式为y=kx+m,
将A(﹣2,0),Q′(6,6)代入y=kx+m,得:,
解得:,
∴直线AO′的解析式为y=x+.
联立直线AO′和直线BC的解析式成方程组,得:,
解得:,
∴点P的坐标为(,).
(3)∵y=﹣x2+2x+6=﹣(x﹣2)2+8,
∴点D的坐标为(2,8).
又∵点C的坐标为(0,6),点B的坐标为(6,0),
∴CD==2,BC═=6,BD═=4,
∴CD2+BC2=BD2,
∴∠BCD=90°.
∵点A的坐标(﹣2,0),点C的坐标为(0,6),
∴OA=2,OC=6,
∴==2,.
又∵∠AOC=∠DCB=90°,
∴△AOC∽△DCB,
∴当Q的坐标为(0,0)时,△AQC∽△DCB.
如图2,连接AC,过点C作CQ⊥AC,交x轴于点Q.
∵△ACQ为直角三角形,CO⊥AQ,
∴△ACQ∽△AOC.
又∵△AOC∽△DCB,
∴△ACQ∽DCB,
∴,即,
∴AQ=20,
∴点Q的坐标为(18,0).
综上所述:当Q的坐标为(0,0)或(18,0)时,以A,C,Q为顶点的三角形与△BCD相似.
20.解:(1)∵直线l1:y=﹣2x+10交y轴于点A,交x轴于点B,
∴点A(0,10),点B(5,0),
∵BC=4,
∴点C(9,0)或点C(1,0),
∵点P1(x1,y1),P2(x2,y2),当x1>x2≥5时,总有y1>y2.
∴当x≥5时,y随x的增大而增大,
当抛物线过点C(9,0)时,则当5<x<7时,y随x的增大而减少,不合题意舍去,
当抛物线过点C(1,0)时,则当x>3时,y随x的增大而增大,符合题意,
∴设抛物线解析式为:y=a(x﹣1)(x﹣5),过点A(0,10),
∴10=5a,
∴a=2,
∴抛物线解析式为:y=2(x﹣1)(x﹣5)=2x2﹣12x+10;
方法二:设抛物线解析式为y=ax2+bx+c,
由题意可得:,
解得:,
∴抛物线解析式为:y=2x2﹣12x+10;
(2)当m=﹣2时,直线l2:y=﹣2x+n(n≠10),
∴直线l2:y=﹣2x+n(n≠10)与直线l1:y=﹣2x+10不重合,
假设l1与l2不平行,则l1与l2必相交,设交点为P(xP,yP),
∴
解得:n=10,
∵n=10与已知n≠10矛盾,
∴l1与l2不相交,
∴l2∥l1;
(3)如图,
、
∵直线l3:y=﹣2x+q过点C,
∴0=﹣2×1+q,
∴q=2,
∴直线l3解析式为:y=﹣2x+2,
∴l3∥l1,
∴CF∥AB,
∴∠ECF=∠ABE,∠CFE=∠BAE,
∴△CEF∽△BEA,
∴=()2,
设BE=t(0<t<4),则CE=4﹣t,
∴S△ABE=×t×10=5t,
∴S△CEF=()2×S△ABE=()2×5t=,
∴S△ABE+S△CEF=5t+=10t+﹣40=10(﹣)2+40﹣40,
∴当t=2时,S△ABE+S△CEF的最小值为40﹣40.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
