2021-2022学年苏科版九年级数学下册5.5用二次函数解决问题同步测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册5.5用二次函数解决问题同步测试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 181.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 19:36:00 | ||
图片预览




文档简介
5.5 用二次函数解决问题 同步测试题
一、 选择题
1. 进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价.若设平均每次降价的百分率是,降价后的价格为元,原价为元,则与之间的函数关系式为( )
A. B. C. D.
2.服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为( )
A. 150元 B. 160元 C. 170元 D. 180元
3.如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( )
A. 60m2 B. 63m2 C. 64m2 D. 66m2
4.某公园有一个圆形喷水池,喷出的水流呈抛物线,一条水流的高度h(单位:m)与水流运动时间t(单位:s)之间的关系式为h=30t﹣5t2 , 那么水流从抛出至回落到地面所需要的时间是( )
A. 6s B. 4s C. 3s D. 2s
5. 一个运动员打高尔夫球,若球的飞行高度与水平距离之间的函数表达式为,则高尔夫球在飞行过程中的最大高度为( )
A. B. C. D.
6. 如图,抛物线与直线相交于点、,是轴上一点,若最小,则点的坐标为( )
A. B. C. D.
7.如图所示,将一根长2m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( )
A.正比例函数关系 B.一次函数关系
C.二次函数关系 D.反比例函数关系
8.如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m B.4m C.4 m D.4m
9.Rt△ABC的三个顶点A,B,C均在抛物线y=x2上,并且斜边AB平行于x轴.若斜边上的高为h,则( )
A.h<1 B.h=1 C.1<h<2 D.h>2
10. 向空中发射一枚炮弹,经秒后的高度为米,且时间与高度的关系为.若此炮弹在第秒与第秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第秒 B.第秒 C.第秒 D.第秒
二、 填空题
11. 将一根长的铁丝围成一矩形,试写出矩形面积与矩形一边长之间的关系式________.
12.如图,抛物线 与直线 的两个交点坐标分别为 , ,则方程 的解是________.
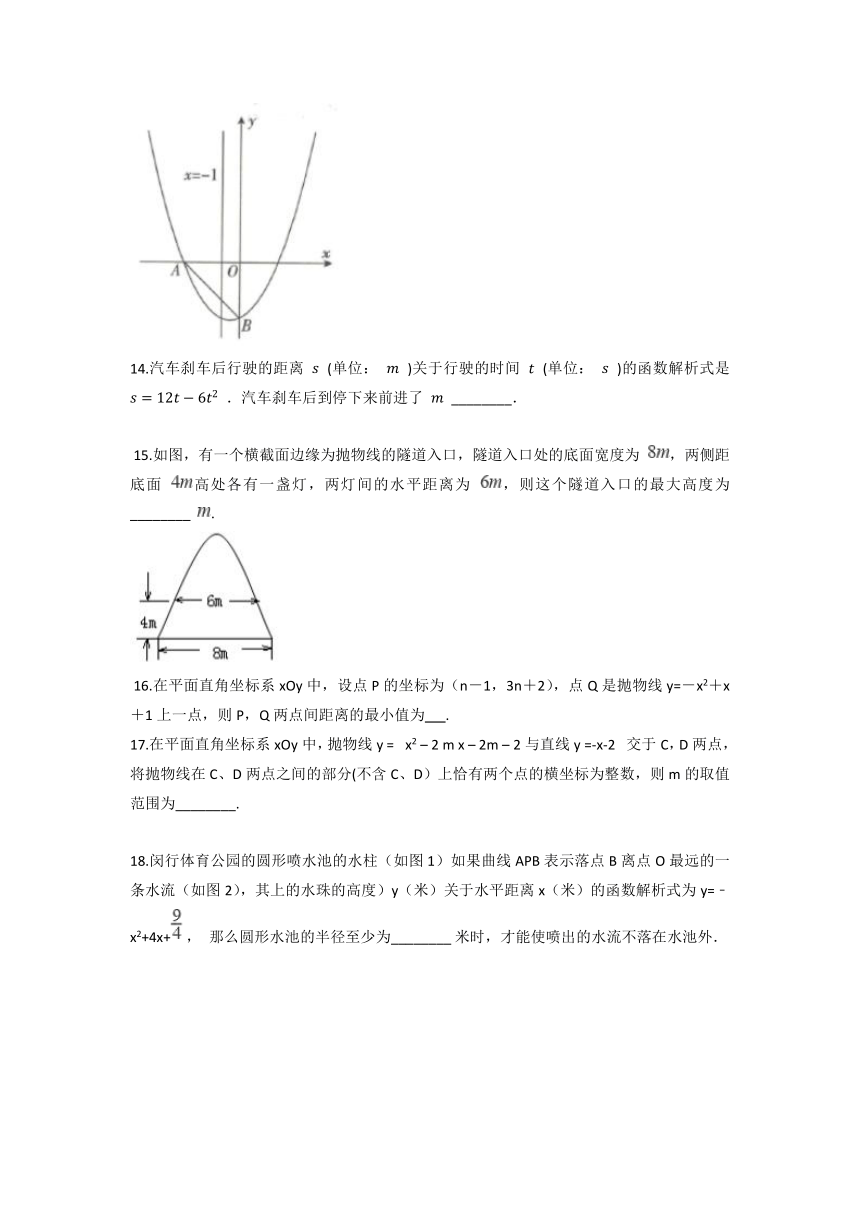
13.如图,抛物线 与 轴的负半轴交于点 ,与 轴交于点 ,连接 ,点 分别是直线 与抛物线上的点,若点 围成的四边形是平行四边形,则点 的坐标为________.
14.汽车刹车后行驶的距离 (单位: )关于行驶的时间 (单位: )的函数解析式是 .汽车刹车后到停下来前进了 ________.
15.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为 ,两侧距底面 高处各有一盏灯,两灯间的水平距离为 ,则这个隧道入口的最大高度为________ .
16.在平面直角坐标系xOy中,设点P的坐标为(n-1,3n+2),点Q是抛物线y=-x2+x+1上一点,则P,Q两点间距离的最小值为 .
17.在平面直角坐标系xOy中,抛物线y = x2 – 2 m x – 2m – 2与直线y =-x-2 交于C,D两点,将抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数,则m的取值范围为________.
18.闵行体育公园的圆形喷水池的水柱(如图1)如果曲线APB表示落点B离点O最远的一条水流(如图2),其上的水珠的高度)y(米)关于水平距离x(米)的函数解析式为y=﹣x2+4x+, 那么圆形水池的半径至少为________ 米时,才能使喷出的水流不落在水池外.
三、 解答题
19.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担,李明按照相关政策投资销售本市生产的一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
⑴李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
⑵设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
⑶物价部门规定,这种节能灯的销售单价不得高于25元,如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
20.某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
21 某动车站在原有的普通售票窗口外新增了无人售票窗口,普通售票窗口从上午点开放,而无人售票窗口从上午点开放,某日从上午点到点,每个普通售票窗口售出的车票数(张)与售票时间(小时)的变化趋势如图,每个无人售票窗口售出的车票数(张)与售票时间(小时)的变化趋势是以原点为顶点的抛物线的一部分,如图,若该日截至上午点,每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同.
求图中所确定抛物线的解析式;
若该日共开放个无人售票窗口,截至上午点,两种窗口共售出的车票数不少于张,则至少需要开放多少个普通售票窗口?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
解:由题意第二次降价后的价格是.
则函数解析式是.
故选.
2.【答案】 A
【考点】二次函数的实际应用-销售问题
解:设获得的利润为y元,由题意得:
∵a=﹣1<0
∴当x=150时,y取得最大值2500元.
故答案为:A .
【分析】设获得的利润为y元,由题意得关于x的二次函数,配方,写成顶点式,利用二次函数的性质可得答案.
3.【答案】 C
【考点】二次函数的实际应用-几何问题
解:设BC=xm,则AB=(16﹣x)m,矩形ABCD面积为ym2 ,
根据题意得:y=(16﹣x)x=﹣x2+16x=﹣(x﹣8)2+64,
当x=8m时,ymax=64m2 ,
则所围成矩形ABCD的最大面积是64m2 .
故选C.
【分析】设BC=xm,表示出AB,矩形面积为ym2 , 表示出y与x的关系式,利用二次函数性质求出面积最大值即可.
4.【答案】 A
【考点】二次函数的实际应用-喷水问题
解:水流从抛出至回落到地面时高度h为0,
把h=0代入h=30t﹣5t2得:5t2﹣30t=0,
解得:t1=0(舍去),t2=6.
故水流从抛出至回落到地面所需要的时间6s.
故选A.
【分析】由于水流从抛出至回落到地面时高度h为0,把h=0代入h=30t﹣5t2即可求出t,也就求出了水流从抛出至回落到地面所需要的时间.
5.
【答案】
A
【解答】
解:在中,
当时,有最大值为.
则高尔夫球在飞行过程中的最大高度为.
故选.
6.
【答案】
C
【解答】
解:如图,作点关于轴的对称点,连接与轴的交点即为点.
当时代入到抛物线解析式得:
,
解得或.
则由图可知点,点,
∴ .
设直线的解析式为:.
代入,求得:,
则该直线与轴的交点为:当时,.
∴ 点.
故选.
7.解:设矩形的一边长为xm,则另一边的长为(2÷2﹣x)m,令矩形的面积为ym2,由题意得:
y=x(2÷2﹣x)
=x(1﹣x)
=﹣x2+x,
∴矩形的面积与其一边满足的函数关系是y=﹣x2+x,即满足二次函数关系.
故选:C.
8.解:根据题意,得
OA=12,OC=4.
所以抛物线的顶点横坐标为6,
即﹣==6,
∴b=2,
∵C(0,4),
∴c=4,
所以抛物线解析式为:
y=﹣x2+2x+4
=﹣(x﹣6)2+10
当y=8时,
8=﹣(x﹣6)2+10,
解得x1=6+2,x2=6﹣2.
则x1﹣x2=4.
所以两排灯的水平距离最小是4.
故选:D.
9.解:由题A,B,C均在抛物线y=x2上,并且斜边AB平行于x轴,
知A、B两点关于y轴对称,记斜边AB交y轴于点D,
可设A(﹣,b),B(,b),C(a,a2),D(0,b)
则因斜边上的高为h,
故:h=b﹣a2,
∵△ABC是直角三角形,由其性质直角三角形斜边中线等于斜边一半,
∴得CD=
∴=,方程两边平方得:(b﹣a2)=(a2﹣b)2
即h=(﹣h)2
因h>0,得h=1,是个定值.
故选:B.
10.
【答案】
B
【解答】
解:∵ 此炮弹在第秒与第秒时的高度相等,
∴ 抛物线的对称轴是:,
∴ 炮弹所在高度最高时:
时间是第秒.
故选.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
【解答】
解:由题意得:矩形的另一边长,
∴ .
故答案为:.
12.【答案】 ,
【考点】二次函数与一次函数的综合应用
【解析】【解答】解:∵抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),
∴方程组 的解为
即关于x的方程ax2-bx-c=0的解为x1=-3,x2=2.
所以方程ax2=bx+c的解是x1=-3,x2=2
故答案为: ,
【分析】将点A,B的坐标分别代入两函数解析式,可求出两函数解析式,再将两函数联立方程组,求出两函数的交点坐标,即可得到关于x的方程ax2-bx-c=0的解。
13.【答案】 或 或
【考点】二次函数图象与坐标轴的交点问题,平行四边形的性质,二次函数的其他应用
【解析】【解答】由抛物线的表达式求得点 的坐标分别为 .
由题意知当 为平行四边形的边时, ,且 ,
∴线段 可由线段 平移得到.
∵点 在直线 上,①当点 的对应点为 时,如图,需先将 向左平移1个单位长度,
此时点 的对应点 的横坐标为 ,将 代入 ,
得 ,∴ .
②当点A的对应点为 时,同理,先将 向右平移2个单位长度,可得点 的对应点 的横坐标为2,
将 代入 得 ,∴
当 为平行四边形的对角线时,可知 的中点坐标为 ,
∵ 在直线 上,
∴根据对称性可知 的横坐标为 ,将 代入
得 ,∴ .
综上所述,点 的坐标为 或 或 .
【分析】根据二次函数 与x轴的负半轴交于点 ,与 轴交于点 .直接令x=0和y=0求出A,B的坐标.再根据平行四边形的性质分情况求出点E的坐标.
14.【答案】 6
【考点】二次函数的其他应用
【解析】【解答】解:根据二次函数解析式 =-6(t -2t+1-1)=-6(t-1) +6
可知,汽车的刹车时间为t=1s,
当t=1时, =12×1-6×1 =6(m)
故答案为:6
【分析】根据二次函数的解析式可得出汽车刹车时时间,将其代入二次函数解析式中即可得出s的值.
15.
【答案】
【解答】
=
=
=,
则小球运动到的最大高度为.
16.【答案】
【考点】相似三角形的判定与性质,二次函数与一次函数的综合应用
【解析】【解答】解:∵点P的坐标为(n-1,3n+2),
∴设x= n-1,y=3n+2,
∴y=3x+5,即:点P在直线y=3x+5上,
设与直线y=3x+5平行的直线为:y=3x+b,
当直线y=3x+b与抛物线y=-x2+x+1相切时,
则3x+b=-x2+x+1,即:x2+2x+b-1=0,
∴ = ,解得:b=2,
∴与直线y=3x+5平行且和抛物线相切的直线为:y=3x+2,此时,直线y=3x+5与直线y=3x+2的距离就是P,Q两点间距离的最小值.
设直线y=3x+5与y轴的交点为C,直线y=3x+2与x,y轴的交点分别为F,E,如图所示,则C(0,5),E(0,2),F( ,0),
∴CE=3,OE=2,OF= ,EF= ,
过点C作CD⊥EF于点D,
∵∠CDE=∠FOE=90°,∠CED=∠FEO,
∴ CDE~ FOE,
∴ ,即 ,解得:CD= ,
∴P,Q两点间距离的最小值为 .
故答案是: .
【分析】先求出点P所在直线的解析式,再求出与点P所在直线平行的直线解析式,然后求出这两条直线间的距离,即可求解.
17.【答案】 -2≤m< 或【考点】二次函数与一次函数的综合应用,二次函数图象上点的坐标特征
【解析】【解答】解:∵在平面直角坐标系xOy中,抛物线y =x2 – 2 m x – 2m – 2与直线y =-x-2交于C,D两点,联立解方程:
解得:
∴抛物线与直线交点的横坐标为:
又∵抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数
∴得出在C、D之间恰有两个整数解
当 即 时得出: 解得:
当 即 时得出: 解得:
故答案为: 或
【分析】先联立解方程将C、D点的横坐标解出来,再根据抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数,得出在C、D之间恰有两个整数解,进行分类讨论即可.
18.【答案】 ①②③⑤
【考点】二次函数图象与系数的关系,二次函数y=ax^2+bx+c的图象,二次函数的其他应用
【解析】【解答】解:①根据图象可知:
a>0,b<0,c<0,
∴abc>0.
∴①符合题意;
②∵抛物线与x轴有两个交点,
∴△>0,即b2-4ac>0,
4ac<b2 .
∴②符合题意;
③∵抛物线的对称轴x<1,
即 ,得2a+b>0.
∴③符合题意;
④∵抛物线与y轴的交点坐标为(0,-2),
∴抛物线的顶点的纵坐标不能为-2.
∴④不符合题意;
⑤根据抛物线的性质可知:
当x<0时,y随x的增大而减小;
∴⑤符合题意;
⑥当x=1时,y<0,
即a+b+c<0.
∴⑥不符合题意.
故答案为①②③⑤.
【分析】①根据抛物线的开口方向、对称轴、与y轴的交点即可判断;②根据抛物线与x轴的交点个数即可判断;③根据抛物线的对称轴即可判断;④根据抛物线与y轴的交点和顶点坐标即可判断;⑤根据抛物线的性质即可判断;⑥根据当x=1时y的值即可判断.
三、解答题
19.【答案】 解:⑴当x=20时,y=-10x+500=-10×20+500=300,
300×(12-10)=300×2=600,
即政府这个月为他承担的总差价为600元.
⑵依题意得,W=(x-10)(-10x+500)=-10x2+600x-5000=-10(x-30)2+4000
∵a=-10<0,∴当x=30时,W有最大值4000.
即当销售单价定为30元时,每月可获得最大利润4000元.
⑶由题意得:-10x2+600x-5000=3000,解得:x1=20,x2=40.
∵a=-10<0,抛物线开口向下,
∴结合图象可知:当20≤x≤40时,W≥3000.
又∵x≤25,
∴当20≤x≤25时,W≥3000.
设政府每个月为他承担的总差价为p元,
∴p=(12-10)×(-10x+500)
=-20x+1000.
∵k=-20<0.
∴p随x的增大而减小,∴当x=25时,p有最小值500.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
【考点】二次函数的实际应用-销售问题,二次函数图象与一元二次方程的综合应用
【解析】【分析】(1)根据销售额=销售量×销售单价,列出函数关系式;
(2)用配方法将(2)的函数关系式变形,利用二次函数的性质求最大值;
(3)把y=3000代入(2)的函数关系式中,解一元二次方程求x,根据x的取值范围求x的值.
三、 解答题
20.
【答案】
想要每月获得元的利润,销售单价应定为元或元.
(3)当销售量每月不小于件时,即,
解得:,
由题意,得:
∴ 当定价元时,新产品每月可获得销售利润最大值是元.
【解答】
解:(1)由题意,得:,
,
(2)由题意,得:,
解这个方程得:,,
答:想要每月获得元的利润,销售单价应定为元或元.
(3)当销售量每月不小于件时,即,
解得:,
由题意,得:
∴ 当定价元时,新产品每月可获得销售利润最大值是元.
21.
【答案】
至少需要开放个普通售票窗口.
【解答】
解:设,
当时,,
把代入,
,
解得:,
∴ .
设,
把,分别代入得:
解得:,
∴ ,
当时,,,
设需要开放个普通售票窗口,
∴ ,
∴ ,
∴ 取整数,
∴ .
答:至少需要开放个普通售票窗口.
一、 选择题
1. 进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价.若设平均每次降价的百分率是,降价后的价格为元,原价为元,则与之间的函数关系式为( )
A. B. C. D.
2.服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为( )
A. 150元 B. 160元 C. 170元 D. 180元
3.如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( )
A. 60m2 B. 63m2 C. 64m2 D. 66m2
4.某公园有一个圆形喷水池,喷出的水流呈抛物线,一条水流的高度h(单位:m)与水流运动时间t(单位:s)之间的关系式为h=30t﹣5t2 , 那么水流从抛出至回落到地面所需要的时间是( )
A. 6s B. 4s C. 3s D. 2s
5. 一个运动员打高尔夫球,若球的飞行高度与水平距离之间的函数表达式为,则高尔夫球在飞行过程中的最大高度为( )
A. B. C. D.
6. 如图,抛物线与直线相交于点、,是轴上一点,若最小,则点的坐标为( )
A. B. C. D.
7.如图所示,将一根长2m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( )
A.正比例函数关系 B.一次函数关系
C.二次函数关系 D.反比例函数关系
8.如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m B.4m C.4 m D.4m
9.Rt△ABC的三个顶点A,B,C均在抛物线y=x2上,并且斜边AB平行于x轴.若斜边上的高为h,则( )
A.h<1 B.h=1 C.1<h<2 D.h>2
10. 向空中发射一枚炮弹,经秒后的高度为米,且时间与高度的关系为.若此炮弹在第秒与第秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第秒 B.第秒 C.第秒 D.第秒
二、 填空题
11. 将一根长的铁丝围成一矩形,试写出矩形面积与矩形一边长之间的关系式________.
12.如图,抛物线 与直线 的两个交点坐标分别为 , ,则方程 的解是________.
13.如图,抛物线 与 轴的负半轴交于点 ,与 轴交于点 ,连接 ,点 分别是直线 与抛物线上的点,若点 围成的四边形是平行四边形,则点 的坐标为________.
14.汽车刹车后行驶的距离 (单位: )关于行驶的时间 (单位: )的函数解析式是 .汽车刹车后到停下来前进了 ________.
15.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为 ,两侧距底面 高处各有一盏灯,两灯间的水平距离为 ,则这个隧道入口的最大高度为________ .
16.在平面直角坐标系xOy中,设点P的坐标为(n-1,3n+2),点Q是抛物线y=-x2+x+1上一点,则P,Q两点间距离的最小值为 .
17.在平面直角坐标系xOy中,抛物线y = x2 – 2 m x – 2m – 2与直线y =-x-2 交于C,D两点,将抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数,则m的取值范围为________.
18.闵行体育公园的圆形喷水池的水柱(如图1)如果曲线APB表示落点B离点O最远的一条水流(如图2),其上的水珠的高度)y(米)关于水平距离x(米)的函数解析式为y=﹣x2+4x+, 那么圆形水池的半径至少为________ 米时,才能使喷出的水流不落在水池外.
三、 解答题
19.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担,李明按照相关政策投资销售本市生产的一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
⑴李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
⑵设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
⑶物价部门规定,这种节能灯的销售单价不得高于25元,如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
20.某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
21 某动车站在原有的普通售票窗口外新增了无人售票窗口,普通售票窗口从上午点开放,而无人售票窗口从上午点开放,某日从上午点到点,每个普通售票窗口售出的车票数(张)与售票时间(小时)的变化趋势如图,每个无人售票窗口售出的车票数(张)与售票时间(小时)的变化趋势是以原点为顶点的抛物线的一部分,如图,若该日截至上午点,每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同.
求图中所确定抛物线的解析式;
若该日共开放个无人售票窗口,截至上午点,两种窗口共售出的车票数不少于张,则至少需要开放多少个普通售票窗口?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
解:由题意第二次降价后的价格是.
则函数解析式是.
故选.
2.【答案】 A
【考点】二次函数的实际应用-销售问题
解:设获得的利润为y元,由题意得:
∵a=﹣1<0
∴当x=150时,y取得最大值2500元.
故答案为:A .
【分析】设获得的利润为y元,由题意得关于x的二次函数,配方,写成顶点式,利用二次函数的性质可得答案.
3.【答案】 C
【考点】二次函数的实际应用-几何问题
解:设BC=xm,则AB=(16﹣x)m,矩形ABCD面积为ym2 ,
根据题意得:y=(16﹣x)x=﹣x2+16x=﹣(x﹣8)2+64,
当x=8m时,ymax=64m2 ,
则所围成矩形ABCD的最大面积是64m2 .
故选C.
【分析】设BC=xm,表示出AB,矩形面积为ym2 , 表示出y与x的关系式,利用二次函数性质求出面积最大值即可.
4.【答案】 A
【考点】二次函数的实际应用-喷水问题
解:水流从抛出至回落到地面时高度h为0,
把h=0代入h=30t﹣5t2得:5t2﹣30t=0,
解得:t1=0(舍去),t2=6.
故水流从抛出至回落到地面所需要的时间6s.
故选A.
【分析】由于水流从抛出至回落到地面时高度h为0,把h=0代入h=30t﹣5t2即可求出t,也就求出了水流从抛出至回落到地面所需要的时间.
5.
【答案】
A
【解答】
解:在中,
当时,有最大值为.
则高尔夫球在飞行过程中的最大高度为.
故选.
6.
【答案】
C
【解答】
解:如图,作点关于轴的对称点,连接与轴的交点即为点.
当时代入到抛物线解析式得:
,
解得或.
则由图可知点,点,
∴ .
设直线的解析式为:.
代入,求得:,
则该直线与轴的交点为:当时,.
∴ 点.
故选.
7.解:设矩形的一边长为xm,则另一边的长为(2÷2﹣x)m,令矩形的面积为ym2,由题意得:
y=x(2÷2﹣x)
=x(1﹣x)
=﹣x2+x,
∴矩形的面积与其一边满足的函数关系是y=﹣x2+x,即满足二次函数关系.
故选:C.
8.解:根据题意,得
OA=12,OC=4.
所以抛物线的顶点横坐标为6,
即﹣==6,
∴b=2,
∵C(0,4),
∴c=4,
所以抛物线解析式为:
y=﹣x2+2x+4
=﹣(x﹣6)2+10
当y=8时,
8=﹣(x﹣6)2+10,
解得x1=6+2,x2=6﹣2.
则x1﹣x2=4.
所以两排灯的水平距离最小是4.
故选:D.
9.解:由题A,B,C均在抛物线y=x2上,并且斜边AB平行于x轴,
知A、B两点关于y轴对称,记斜边AB交y轴于点D,
可设A(﹣,b),B(,b),C(a,a2),D(0,b)
则因斜边上的高为h,
故:h=b﹣a2,
∵△ABC是直角三角形,由其性质直角三角形斜边中线等于斜边一半,
∴得CD=
∴=,方程两边平方得:(b﹣a2)=(a2﹣b)2
即h=(﹣h)2
因h>0,得h=1,是个定值.
故选:B.
10.
【答案】
B
【解答】
解:∵ 此炮弹在第秒与第秒时的高度相等,
∴ 抛物线的对称轴是:,
∴ 炮弹所在高度最高时:
时间是第秒.
故选.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
【解答】
解:由题意得:矩形的另一边长,
∴ .
故答案为:.
12.【答案】 ,
【考点】二次函数与一次函数的综合应用
【解析】【解答】解:∵抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),
∴方程组 的解为
即关于x的方程ax2-bx-c=0的解为x1=-3,x2=2.
所以方程ax2=bx+c的解是x1=-3,x2=2
故答案为: ,
【分析】将点A,B的坐标分别代入两函数解析式,可求出两函数解析式,再将两函数联立方程组,求出两函数的交点坐标,即可得到关于x的方程ax2-bx-c=0的解。
13.【答案】 或 或
【考点】二次函数图象与坐标轴的交点问题,平行四边形的性质,二次函数的其他应用
【解析】【解答】由抛物线的表达式求得点 的坐标分别为 .
由题意知当 为平行四边形的边时, ,且 ,
∴线段 可由线段 平移得到.
∵点 在直线 上,①当点 的对应点为 时,如图,需先将 向左平移1个单位长度,
此时点 的对应点 的横坐标为 ,将 代入 ,
得 ,∴ .
②当点A的对应点为 时,同理,先将 向右平移2个单位长度,可得点 的对应点 的横坐标为2,
将 代入 得 ,∴
当 为平行四边形的对角线时,可知 的中点坐标为 ,
∵ 在直线 上,
∴根据对称性可知 的横坐标为 ,将 代入
得 ,∴ .
综上所述,点 的坐标为 或 或 .
【分析】根据二次函数 与x轴的负半轴交于点 ,与 轴交于点 .直接令x=0和y=0求出A,B的坐标.再根据平行四边形的性质分情况求出点E的坐标.
14.【答案】 6
【考点】二次函数的其他应用
【解析】【解答】解:根据二次函数解析式 =-6(t -2t+1-1)=-6(t-1) +6
可知,汽车的刹车时间为t=1s,
当t=1时, =12×1-6×1 =6(m)
故答案为:6
【分析】根据二次函数的解析式可得出汽车刹车时时间,将其代入二次函数解析式中即可得出s的值.
15.
【答案】
【解答】
=
=
=,
则小球运动到的最大高度为.
16.【答案】
【考点】相似三角形的判定与性质,二次函数与一次函数的综合应用
【解析】【解答】解:∵点P的坐标为(n-1,3n+2),
∴设x= n-1,y=3n+2,
∴y=3x+5,即:点P在直线y=3x+5上,
设与直线y=3x+5平行的直线为:y=3x+b,
当直线y=3x+b与抛物线y=-x2+x+1相切时,
则3x+b=-x2+x+1,即:x2+2x+b-1=0,
∴ = ,解得:b=2,
∴与直线y=3x+5平行且和抛物线相切的直线为:y=3x+2,此时,直线y=3x+5与直线y=3x+2的距离就是P,Q两点间距离的最小值.
设直线y=3x+5与y轴的交点为C,直线y=3x+2与x,y轴的交点分别为F,E,如图所示,则C(0,5),E(0,2),F( ,0),
∴CE=3,OE=2,OF= ,EF= ,
过点C作CD⊥EF于点D,
∵∠CDE=∠FOE=90°,∠CED=∠FEO,
∴ CDE~ FOE,
∴ ,即 ,解得:CD= ,
∴P,Q两点间距离的最小值为 .
故答案是: .
【分析】先求出点P所在直线的解析式,再求出与点P所在直线平行的直线解析式,然后求出这两条直线间的距离,即可求解.
17.【答案】 -2≤m< 或
【解析】【解答】解:∵在平面直角坐标系xOy中,抛物线y =x2 – 2 m x – 2m – 2与直线y =-x-2交于C,D两点,联立解方程:
解得:
∴抛物线与直线交点的横坐标为:
又∵抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数
∴得出在C、D之间恰有两个整数解
当 即 时得出: 解得:
当 即 时得出: 解得:
故答案为: 或
【分析】先联立解方程将C、D点的横坐标解出来,再根据抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数,得出在C、D之间恰有两个整数解,进行分类讨论即可.
18.【答案】 ①②③⑤
【考点】二次函数图象与系数的关系,二次函数y=ax^2+bx+c的图象,二次函数的其他应用
【解析】【解答】解:①根据图象可知:
a>0,b<0,c<0,
∴abc>0.
∴①符合题意;
②∵抛物线与x轴有两个交点,
∴△>0,即b2-4ac>0,
4ac<b2 .
∴②符合题意;
③∵抛物线的对称轴x<1,
即 ,得2a+b>0.
∴③符合题意;
④∵抛物线与y轴的交点坐标为(0,-2),
∴抛物线的顶点的纵坐标不能为-2.
∴④不符合题意;
⑤根据抛物线的性质可知:
当x<0时,y随x的增大而减小;
∴⑤符合题意;
⑥当x=1时,y<0,
即a+b+c<0.
∴⑥不符合题意.
故答案为①②③⑤.
【分析】①根据抛物线的开口方向、对称轴、与y轴的交点即可判断;②根据抛物线与x轴的交点个数即可判断;③根据抛物线的对称轴即可判断;④根据抛物线与y轴的交点和顶点坐标即可判断;⑤根据抛物线的性质即可判断;⑥根据当x=1时y的值即可判断.
三、解答题
19.【答案】 解:⑴当x=20时,y=-10x+500=-10×20+500=300,
300×(12-10)=300×2=600,
即政府这个月为他承担的总差价为600元.
⑵依题意得,W=(x-10)(-10x+500)=-10x2+600x-5000=-10(x-30)2+4000
∵a=-10<0,∴当x=30时,W有最大值4000.
即当销售单价定为30元时,每月可获得最大利润4000元.
⑶由题意得:-10x2+600x-5000=3000,解得:x1=20,x2=40.
∵a=-10<0,抛物线开口向下,
∴结合图象可知:当20≤x≤40时,W≥3000.
又∵x≤25,
∴当20≤x≤25时,W≥3000.
设政府每个月为他承担的总差价为p元,
∴p=(12-10)×(-10x+500)
=-20x+1000.
∵k=-20<0.
∴p随x的增大而减小,∴当x=25时,p有最小值500.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
【考点】二次函数的实际应用-销售问题,二次函数图象与一元二次方程的综合应用
【解析】【分析】(1)根据销售额=销售量×销售单价,列出函数关系式;
(2)用配方法将(2)的函数关系式变形,利用二次函数的性质求最大值;
(3)把y=3000代入(2)的函数关系式中,解一元二次方程求x,根据x的取值范围求x的值.
三、 解答题
20.
【答案】
想要每月获得元的利润,销售单价应定为元或元.
(3)当销售量每月不小于件时,即,
解得:,
由题意,得:
∴ 当定价元时,新产品每月可获得销售利润最大值是元.
【解答】
解:(1)由题意,得:,
,
(2)由题意,得:,
解这个方程得:,,
答:想要每月获得元的利润,销售单价应定为元或元.
(3)当销售量每月不小于件时,即,
解得:,
由题意,得:
∴ 当定价元时,新产品每月可获得销售利润最大值是元.
21.
【答案】
至少需要开放个普通售票窗口.
【解答】
解:设,
当时,,
把代入,
,
解得:,
∴ .
设,
把,分别代入得:
解得:,
∴ ,
当时,,,
设需要开放个普通售票窗口,
∴ ,
∴ ,
∴ 取整数,
∴ .
答:至少需要开放个普通售票窗口.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
