2.1简谐运动基础巩固(word版含答案)
文档属性
| 名称 | 2.1简谐运动基础巩固(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 300.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-16 08:10:35 | ||
图片预览



文档简介
2.1简谐运动基础巩固2021—2022学年高中物理粤教版(2019)选择性必修第一册
一、选择题(共14题)
1.水平弹簧振子在运动过程中,不发生的变化的是( )
A.动能 B.机械能 C.回复力 D.弹性势能
2.下列运动可以看成机械振动的是
A.秋风中树叶下落
B.声带发声
C.音叉被移动
D.火车沿斜坡行驶
3.下列日常生活中常见情形中不属于机械振动的是( )
A.水中浮标上下浮动 B.秋千的摆动
C.拨动后的琴弦 D.表针沿表盘转动
4.质点运动的位移 x 与时间 t 的关系如图所示,其中不属于机械振动的是
A. B.
C. D.
5.关于简谐运动的位移、加速度和速度的关系,下列说法中正确的是( )
A.位移减少时,加速度减少,速度也减少
B.位移方向总是跟加速度方向相反,跟速度方向相同
C.物体的运动方向指向平衡位置时,速度方向跟位移方向相反;背离平衡位置时,速度方向跟位移方向相同
D.物体向负方向运动时,加速度方向跟速度方向相同;向正方向运动时,加速度方向跟速度方向相反
6.关于单摆,下列说法中正确的是( ).
A.摆球运动的回复力是摆线拉力与重力的合力
B.摆球在运动过程中经过轨迹上的同一点时,加速度是不变的
C.摆球在运动过程中加速度方向始终指向平衡位置
D.摆球经过平衡位置时,加速度为零
7.关于简谐运动,下列说法正确的是( )
A.位移的方向总指向平衡位置
B.加速度方向总和位移方向相反
C.位移方向总和速度方向相反
D.速度方向总和位移方向相同
8.关于简谐振动的加速度,下列说法正确的是
A.大小与位移成正比,方向周期变化一次
B.大小不变,方向始终指向平衡位置
C.大小与位移成正比,方向始终指向平衡位置
D.大小变化是均匀的,方向一周期变化一次
9.简谐运动是下列哪一种运动( )
A.匀速直线运动
B.匀加速直线运动
C.匀变速运动
D.变加速运动
10.如图所示,一轻弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点。已知OC=h,弹簧的劲度系数为k,某时刻物体恰好以大小为v的速度经过C点并向上运动,则从此时刻开始的半个周期时间内,对质量为m的物体,下列说法不正确的是( )
A.重力势能减少了2mgh
B.回复力做功为2mgh
C.回复力的冲量大小为2mv
D.通过A点时回复力的大小为2kh
11.图为一质点做简谐运动的位移随时间变化的图像,由图可知,在t=4s 时刻,质点的( )
A.速度为零,位移为正的最大值
B.速度为零,位移为负的最大值
C.速度为正的最大值,位移为零
D.速度为负的最大值,位移为零
12.把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它的平衡位置为O,在A、B间振动,如图所示,下列结论正确的是( )
A.小球在O位置时,动能最大,加速度最小
B.小球在A、B位置时,动能最大,加速度最大
C.小球从A经O到B的过程中,回复力一直做正功
D.小球从A经O到B的过程中,回复力一直做负功
13.弹簧振子在从一端向平衡位置运动的过程中( )
A.速度增大,振幅减小 B.速度增大,加速度也增大
C.速度增大,加速度减小 D.速度与加速度的方向相反
14.下列说法正确的是
A.在同一地点,当摆长不变时,摆球质量越大,单摆做简谐振动的周期越小
B.已知弹簧振子初始时刻的位置及振动周期,就可知振子任意时刻运动速度的方向
C.当一列声波从空气中传入水中时,因水的阻力作用,波长一定会变短
D.医院检查身体的“彩超”仪利用了超声波的多普勒效应
二、填空题(共4题)
15.被拍打的篮球上下运动不是简谐运动(______)
16.弹簧振子
(1)机械振动:物体或物体的一部分在一个位置附近的_____运动,简称振动。
(2)弹簧振子:_____和弹簧组成的系统。
17.回复力是根据力的_______命名的.弹簧振子是一个典型的简谐运动模型,它的回复力是由_____提供的.
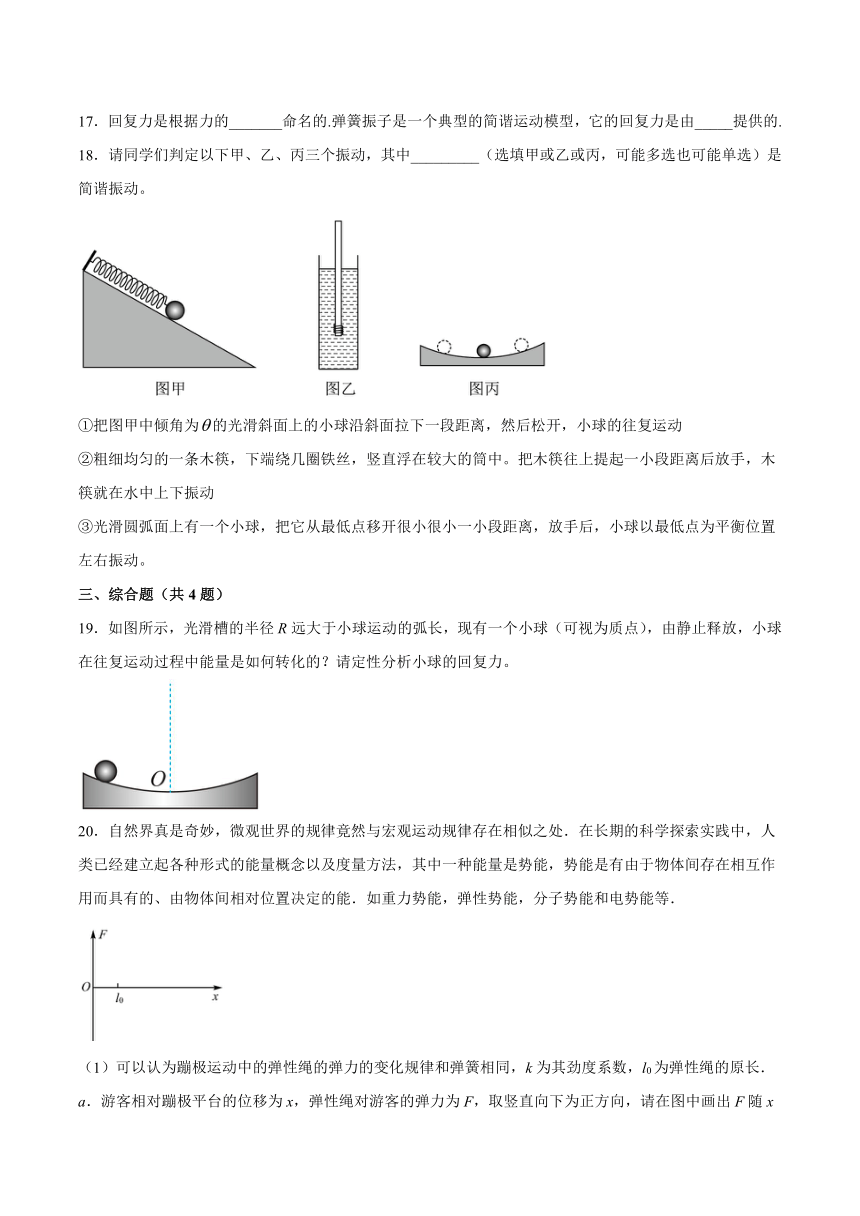
18.请同学们判定以下甲、乙、丙三个振动,其中_________(选填甲或乙或丙,可能多选也可能单选)是简谐振动。
①把图甲中倾角为的光滑斜面上的小球沿斜面拉下一段距离,然后松开,小球的往复运动
②粗细均匀的一条木筷,下端绕几圈铁丝,竖直浮在较大的筒中。把木筷往上提起一小段距离后放手,木筷就在水中上下振动
③光滑圆弧面上有一个小球,把它从最低点移开很小很小一小段距离,放手后,小球以最低点为平衡位置左右振动。
三、综合题(共4题)
19.如图所示,光滑槽的半径R远大于小球运动的弧长,现有一个小球(可视为质点),由静止释放,小球在往复运动过程中能量是如何转化的?请定性分析小球的回复力。
20.自然界真是奇妙,微观世界的规律竟然与宏观运动规律存在相似之处.在长期的科学探索实践中,人类已经建立起各种形式的能量概念以及度量方法,其中一种能量是势能,势能是有由于物体间存在相互作用而具有的、由物体间相对位置决定的能.如重力势能,弹性势能,分子势能和电势能等.
(1)可以认为蹦极运动中的弹性绳的弹力的变化规律和弹簧相同,k为其劲度系数,l0为弹性绳的原长.
a.游客相对蹦极平台的位移为x,弹性绳对游客的弹力为F,取竖直向下为正方向,请在图中画出F随x变化的示意图,并借助F-x图像推导当游客位移为x(x>l0)时,弹性绳弹性势能EP的表达式;
b.已知l0=10m,k=100N/m,蹦极平台与地面间的距离D=55m.取重力加速度g=10m/s2.计算总质量M=160kg的游客使用该蹦极设施时距离地面的最小距离.
(2)如图甲所示,a、b为某种物质的两个分子,假设分子a固定不动,分子b只在ab间分子力的作用下运动(在x轴上),以a为原点,沿两分子连线建立x轴.两个分子之间的作用力与它们之间距离x的F-x关系图线如图乙所示.图线在r0处的斜率为k,当分子b在两分子间距r0附近小范围振动时.
a.弹簧、橡皮筋等弹性物质,大多有“弹性限度”,在“弹性限度”范围遵守胡克定律,请结合图乙从微观尺度上谈谈你对“弹性限度”范围的理解.说明在“弹性限度”范围内,微观层面上分子b的运动形式;
b.推导两分子间距为x(x>r0)时,两分子间分子势能EP的表达式;当两分子间距离为r0时,b分子的动能为Ek0.求两分子在r0附近小范围振动时的振动范围.当温度小范围升高时,热运动加剧,A同学认为分子振动范围变大,B同学认为分子振动频率变大,哪位同学的观点正确?
21.如图所示,盛水(密度为ρ1)容器的水面上漂浮着一块质量分布均匀的高为h、底面积为S的长方体木块(密度为ρ2),浸入水中的深度为a,O为木块质心,现在将木块相对于原来静止的位置轻轻按下距离A(木块没有完全浸没),木块就在水面上下振动(木块始终没有离开水面),不考虑任何阻力,重力加速度为g,试证明木块做简谐运动。
22.如图所示为一弹簧振子在A、C间振动,图中黑点为振子球心的位置。
(1)画出振子位于C点时离开平衡位置O的位移;
(2)标出振子位于A点时加速度的方向。
参考答案
1.B
2.B
3.D
4.D
5.C
6.B
7.B
8.C
9.D
10.B
11.A
12.A
13.C
14.D
15.正确
16.往复 小球(或物体)
17.效果 弹簧的弹力
18.甲乙丙
19.
设小球从A静止释放,如图
从,小球的重力势能转化为动能,从,动能转化为重力势能,从,小球的重力势能转化为动能,从,动能转化为重力势能,周而复始,其中小球在O点速度最大,在A、B点速度为零;
在运动过程中小球的回复力,由小球重力沿圆弧切线方向的分力提供。
20.(1)a. b.(2)a.弹力是分子力的宏观表现,从微观尺度上看,只有在r0附近,分子力才和分子偏离r0的距离成正比,宏观上表现为“弹性限度”范围.简谐运动b.振动范围温度升高,Ek0增大,振动范围增大,频率不变.
21.
木块的平衡位置就在原来静止的位置,木块漂浮(静止)时由力平衡可得
G=F浮
即
ρ2ghS=ρ1gSa
现在以木块振动到平衡位置下方情形为例来证明,设木块振动到平衡位置下方x时(x≤A),其偏离平衡位置的位移大小为x,所受到的浮力变为
回复力为
解得
F回=ρ1gSx
显然回复力大小与偏离平衡位置的位移大小成正比,同理可证,木块振动到平衡位置上方时回复力大小与偏离平衡位置的位移大小成正比,分析木块在平衡位置上方和下方时的回复力方向可知,回复力恒指向平衡位置,所以木块此时做简谐运动。
22.(1) ;(2)
一、选择题(共14题)
1.水平弹簧振子在运动过程中,不发生的变化的是( )
A.动能 B.机械能 C.回复力 D.弹性势能
2.下列运动可以看成机械振动的是
A.秋风中树叶下落
B.声带发声
C.音叉被移动
D.火车沿斜坡行驶
3.下列日常生活中常见情形中不属于机械振动的是( )
A.水中浮标上下浮动 B.秋千的摆动
C.拨动后的琴弦 D.表针沿表盘转动
4.质点运动的位移 x 与时间 t 的关系如图所示,其中不属于机械振动的是
A. B.
C. D.
5.关于简谐运动的位移、加速度和速度的关系,下列说法中正确的是( )
A.位移减少时,加速度减少,速度也减少
B.位移方向总是跟加速度方向相反,跟速度方向相同
C.物体的运动方向指向平衡位置时,速度方向跟位移方向相反;背离平衡位置时,速度方向跟位移方向相同
D.物体向负方向运动时,加速度方向跟速度方向相同;向正方向运动时,加速度方向跟速度方向相反
6.关于单摆,下列说法中正确的是( ).
A.摆球运动的回复力是摆线拉力与重力的合力
B.摆球在运动过程中经过轨迹上的同一点时,加速度是不变的
C.摆球在运动过程中加速度方向始终指向平衡位置
D.摆球经过平衡位置时,加速度为零
7.关于简谐运动,下列说法正确的是( )
A.位移的方向总指向平衡位置
B.加速度方向总和位移方向相反
C.位移方向总和速度方向相反
D.速度方向总和位移方向相同
8.关于简谐振动的加速度,下列说法正确的是
A.大小与位移成正比,方向周期变化一次
B.大小不变,方向始终指向平衡位置
C.大小与位移成正比,方向始终指向平衡位置
D.大小变化是均匀的,方向一周期变化一次
9.简谐运动是下列哪一种运动( )
A.匀速直线运动
B.匀加速直线运动
C.匀变速运动
D.变加速运动
10.如图所示,一轻弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点。已知OC=h,弹簧的劲度系数为k,某时刻物体恰好以大小为v的速度经过C点并向上运动,则从此时刻开始的半个周期时间内,对质量为m的物体,下列说法不正确的是( )
A.重力势能减少了2mgh
B.回复力做功为2mgh
C.回复力的冲量大小为2mv
D.通过A点时回复力的大小为2kh
11.图为一质点做简谐运动的位移随时间变化的图像,由图可知,在t=4s 时刻,质点的( )
A.速度为零,位移为正的最大值
B.速度为零,位移为负的最大值
C.速度为正的最大值,位移为零
D.速度为负的最大值,位移为零
12.把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它的平衡位置为O,在A、B间振动,如图所示,下列结论正确的是( )
A.小球在O位置时,动能最大,加速度最小
B.小球在A、B位置时,动能最大,加速度最大
C.小球从A经O到B的过程中,回复力一直做正功
D.小球从A经O到B的过程中,回复力一直做负功
13.弹簧振子在从一端向平衡位置运动的过程中( )
A.速度增大,振幅减小 B.速度增大,加速度也增大
C.速度增大,加速度减小 D.速度与加速度的方向相反
14.下列说法正确的是
A.在同一地点,当摆长不变时,摆球质量越大,单摆做简谐振动的周期越小
B.已知弹簧振子初始时刻的位置及振动周期,就可知振子任意时刻运动速度的方向
C.当一列声波从空气中传入水中时,因水的阻力作用,波长一定会变短
D.医院检查身体的“彩超”仪利用了超声波的多普勒效应
二、填空题(共4题)
15.被拍打的篮球上下运动不是简谐运动(______)
16.弹簧振子
(1)机械振动:物体或物体的一部分在一个位置附近的_____运动,简称振动。
(2)弹簧振子:_____和弹簧组成的系统。
17.回复力是根据力的_______命名的.弹簧振子是一个典型的简谐运动模型,它的回复力是由_____提供的.
18.请同学们判定以下甲、乙、丙三个振动,其中_________(选填甲或乙或丙,可能多选也可能单选)是简谐振动。
①把图甲中倾角为的光滑斜面上的小球沿斜面拉下一段距离,然后松开,小球的往复运动
②粗细均匀的一条木筷,下端绕几圈铁丝,竖直浮在较大的筒中。把木筷往上提起一小段距离后放手,木筷就在水中上下振动
③光滑圆弧面上有一个小球,把它从最低点移开很小很小一小段距离,放手后,小球以最低点为平衡位置左右振动。
三、综合题(共4题)
19.如图所示,光滑槽的半径R远大于小球运动的弧长,现有一个小球(可视为质点),由静止释放,小球在往复运动过程中能量是如何转化的?请定性分析小球的回复力。
20.自然界真是奇妙,微观世界的规律竟然与宏观运动规律存在相似之处.在长期的科学探索实践中,人类已经建立起各种形式的能量概念以及度量方法,其中一种能量是势能,势能是有由于物体间存在相互作用而具有的、由物体间相对位置决定的能.如重力势能,弹性势能,分子势能和电势能等.
(1)可以认为蹦极运动中的弹性绳的弹力的变化规律和弹簧相同,k为其劲度系数,l0为弹性绳的原长.
a.游客相对蹦极平台的位移为x,弹性绳对游客的弹力为F,取竖直向下为正方向,请在图中画出F随x变化的示意图,并借助F-x图像推导当游客位移为x(x>l0)时,弹性绳弹性势能EP的表达式;
b.已知l0=10m,k=100N/m,蹦极平台与地面间的距离D=55m.取重力加速度g=10m/s2.计算总质量M=160kg的游客使用该蹦极设施时距离地面的最小距离.
(2)如图甲所示,a、b为某种物质的两个分子,假设分子a固定不动,分子b只在ab间分子力的作用下运动(在x轴上),以a为原点,沿两分子连线建立x轴.两个分子之间的作用力与它们之间距离x的F-x关系图线如图乙所示.图线在r0处的斜率为k,当分子b在两分子间距r0附近小范围振动时.
a.弹簧、橡皮筋等弹性物质,大多有“弹性限度”,在“弹性限度”范围遵守胡克定律,请结合图乙从微观尺度上谈谈你对“弹性限度”范围的理解.说明在“弹性限度”范围内,微观层面上分子b的运动形式;
b.推导两分子间距为x(x>r0)时,两分子间分子势能EP的表达式;当两分子间距离为r0时,b分子的动能为Ek0.求两分子在r0附近小范围振动时的振动范围.当温度小范围升高时,热运动加剧,A同学认为分子振动范围变大,B同学认为分子振动频率变大,哪位同学的观点正确?
21.如图所示,盛水(密度为ρ1)容器的水面上漂浮着一块质量分布均匀的高为h、底面积为S的长方体木块(密度为ρ2),浸入水中的深度为a,O为木块质心,现在将木块相对于原来静止的位置轻轻按下距离A(木块没有完全浸没),木块就在水面上下振动(木块始终没有离开水面),不考虑任何阻力,重力加速度为g,试证明木块做简谐运动。
22.如图所示为一弹簧振子在A、C间振动,图中黑点为振子球心的位置。
(1)画出振子位于C点时离开平衡位置O的位移;
(2)标出振子位于A点时加速度的方向。
参考答案
1.B
2.B
3.D
4.D
5.C
6.B
7.B
8.C
9.D
10.B
11.A
12.A
13.C
14.D
15.正确
16.往复 小球(或物体)
17.效果 弹簧的弹力
18.甲乙丙
19.
设小球从A静止释放,如图
从,小球的重力势能转化为动能,从,动能转化为重力势能,从,小球的重力势能转化为动能,从,动能转化为重力势能,周而复始,其中小球在O点速度最大,在A、B点速度为零;
在运动过程中小球的回复力,由小球重力沿圆弧切线方向的分力提供。
20.(1)a. b.(2)a.弹力是分子力的宏观表现,从微观尺度上看,只有在r0附近,分子力才和分子偏离r0的距离成正比,宏观上表现为“弹性限度”范围.简谐运动b.振动范围温度升高,Ek0增大,振动范围增大,频率不变.
21.
木块的平衡位置就在原来静止的位置,木块漂浮(静止)时由力平衡可得
G=F浮
即
ρ2ghS=ρ1gSa
现在以木块振动到平衡位置下方情形为例来证明,设木块振动到平衡位置下方x时(x≤A),其偏离平衡位置的位移大小为x,所受到的浮力变为
回复力为
解得
F回=ρ1gSx
显然回复力大小与偏离平衡位置的位移大小成正比,同理可证,木块振动到平衡位置上方时回复力大小与偏离平衡位置的位移大小成正比,分析木块在平衡位置上方和下方时的回复力方向可知,回复力恒指向平衡位置,所以木块此时做简谐运动。
22.(1) ;(2)
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
