2021—2022学年人教版数学七年级下册第五章相交线与平行线复习课件(20张)
文档属性
| 名称 | 2021—2022学年人教版数学七年级下册第五章相交线与平行线复习课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 14.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
相交线与平行线小结
学习目标
1.使学生认识平面内两条直线的位 置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案.
经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化,梳理本章的知识结构.
通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形
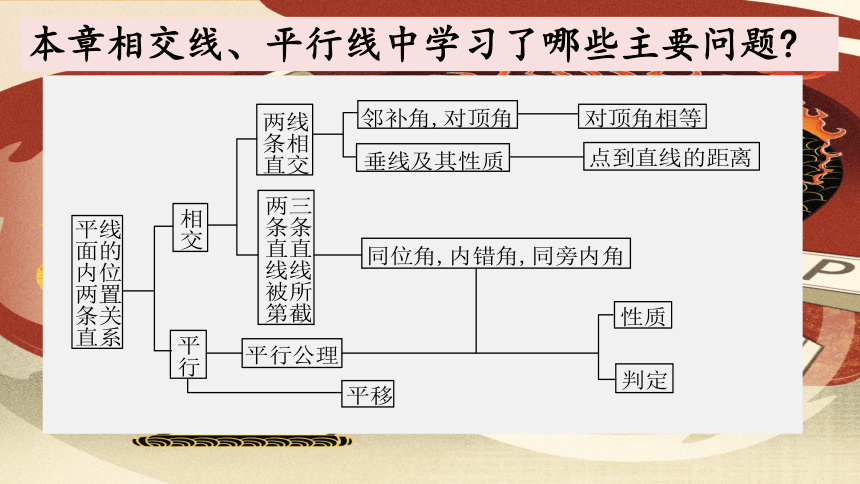
本章相交线、平行线中学习了哪些主要问题
1.对顶角、邻补角
有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
(1)邻补角互补.但两个角的和等于180°,这两个角不一定是邻补角. (2)对顶角相等.但反过来,相等的两个角不一定是对顶角
有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
邻补角、对顶角是成对出现的,在相交直线中,一个角的邻补角有两个
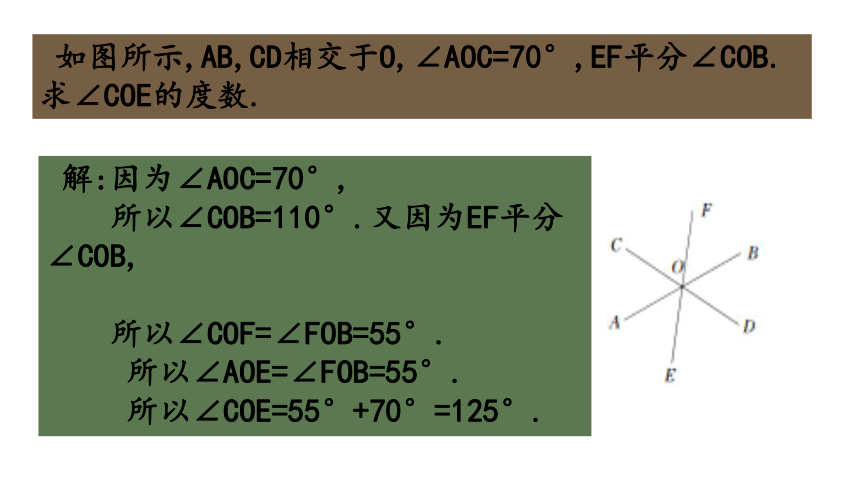
如图所示,AB,CD相交于O,∠AOC=70°,EF平分∠COB.求∠COE的度数.
解:因为∠AOC=70°,
所以∠COB=110°.又因为EF平分∠COB,
所以∠COF=∠FOB=55°.
所以∠AOE=∠FOB=55°.
所以∠COE=55°+70°=125°.
在同一平面内,过一点有且只有一条直线与已知直线垂直.
“有且只有”中,“有”指“存在性”,“只有”指“唯一性”.
“过一点”中的“点”在直线上或直线外都可以.
垂线的性质:
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
垂线的概念:
3
2
4.点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
下列四个条件中能判断两条直线互相垂直的有 ( )①两条直线相交所成的四个角中,有一个角是直角;②两条直线相交所成的四个角相等;③两条直线相交所成的四个角中,有一组相邻的角相等;④两条直线相交所成的四个角中,有一组对顶角的和为180°.A.4个 B.3个 C.2个 D.1个
A
1.构成同位角、内错角、同旁内角的一对角研究的是三条直线相交的角的情况;
2.同位角、内错角、同旁内角这三类角都是一种位置关系,而不是大小关系;
3.同位角、内错角、同旁内角总是成对出现的;
4.判断“三线八角”中的两个角的位置关系,同位角为“F”形,内错角为“Z”形,同旁内角为“U”形,截线是这些角的边所共有的直线.
5.三线八角
如图所示,将一块三角板镶嵌在两根木棒(AD与AE)之间(木棒可看成是线段),则图中共有 对同旁内角.
4
1.平行线是在同一平面内具有特殊位置关系的两条直线.平行线没有公共点,但没有交点未必就平行,只有在“同一平面内”才平行;
2.平行线指的是“两条直线”,而不是两条线段或射线,若说两条线段(射线)平行,则指的是两条线段(射线)所在的直线平行;
3.“不相交”就是说两条直线没有交点,即没有公共点;
4.平行关系是相互的,若AB∥CD,也可写作CD∥AB;
5.平行公理中的“有”是指存在性,即“经过直线外一点,有一条直线与已知直线平行”,“只有”是指唯一性,即“经过直线外一点,只有一条直线与已知直线平行”.二者缺一不可.
6.平行线的判定及平行公理
7.判断两条直线平行的步骤:先找同位角或内错角,看它们是否相等;若没有,再找同旁内角,看它们是否互补;若还没有,再找题中有无对顶角等可以转换为同位角、内错角或同旁内角;若没有,看两条直线是否平行于第三条直线.
如图所示,已知∠1=∠2,AC平分∠DAB,试说明DC∥AB.
解:因为AC平分∠DAB(已知),
所以∠1=∠CAB(角平分线定义).
又因为∠1=∠2(已知),
所以∠CAB=∠2(等量代换).
所以AB∥CD(内错角相等,两直线平行).
8.平行线的性质
1.平行线的性质与判定的联系与区别.联系:性质与判定的已知和结论正好相反,都是角的关系与平行线相关.区别:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行.
2.同位角相等、同旁内角互补、内错角相等,都是平行线特有的性质,且不可忽略前提条件“两直线平行”,不要看到同位角或内错角,就认为是相等的.
如图所示,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
解:因为EF∥BC,
所以∠BAF=180°-∠B=100°,
因为AC平分∠BAF,
所以∠CAF=∠BAF=50°,
因为EF∥BC,
所以∠C=∠CAF=50°
9.命题,定理。证明
1.必须是对某件事情作出判断的句子,才能叫命题,反之不能作出判断的句子,不叫命题,这是辨别一个语句是否是命题的根本原则.
2.命题的形式并非全部是语言叙述的形式,也可以用数学符号表示.
3.命题的内容并非全部为数学语言,还有生活中其他方面更广泛的内涵.
说出下列命题的题设和结论.
(1)互为邻补角的两个角的平分线互相垂直;
(2)钝角大于它的补角.
(1)题设:两角互为邻补角,结论:它们的平分线互相垂直.
(2)题设:一个角是钝角,结论:这个角大于它的补角.
9.平移
1.平移是图形的基本变换,方向和距离是平移变换的基本要素:平移的方向,它可以是上、下、左、右或用方向角表示;平移的距离就是新图形与原图形对应点连线的长度.
2.平移时图形的所有点移动方向一致,并且移动的距离相等,所以确定一个图形平移的方向和距离,只需确定其中一个点平移的方向和距离.
3.平移与平行有关,平移可以将一个角、一条线段、一个图形平移到另一个位置,使分散的条件集中到一个图形上,便于解决问题.
关于图形平移,下列结论错误的是 ( )A.对应线段相等B.对应角相等C.对应点所连的线段互相平分D.对应点所连的线段相等
c
相交线与平行线小结
学习目标
1.使学生认识平面内两条直线的位 置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案.
经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化,梳理本章的知识结构.
通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形
本章相交线、平行线中学习了哪些主要问题
1.对顶角、邻补角
有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
(1)邻补角互补.但两个角的和等于180°,这两个角不一定是邻补角. (2)对顶角相等.但反过来,相等的两个角不一定是对顶角
有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
邻补角、对顶角是成对出现的,在相交直线中,一个角的邻补角有两个
如图所示,AB,CD相交于O,∠AOC=70°,EF平分∠COB.求∠COE的度数.
解:因为∠AOC=70°,
所以∠COB=110°.又因为EF平分∠COB,
所以∠COF=∠FOB=55°.
所以∠AOE=∠FOB=55°.
所以∠COE=55°+70°=125°.
在同一平面内,过一点有且只有一条直线与已知直线垂直.
“有且只有”中,“有”指“存在性”,“只有”指“唯一性”.
“过一点”中的“点”在直线上或直线外都可以.
垂线的性质:
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
垂线的概念:
3
2
4.点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
下列四个条件中能判断两条直线互相垂直的有 ( )①两条直线相交所成的四个角中,有一个角是直角;②两条直线相交所成的四个角相等;③两条直线相交所成的四个角中,有一组相邻的角相等;④两条直线相交所成的四个角中,有一组对顶角的和为180°.A.4个 B.3个 C.2个 D.1个
A
1.构成同位角、内错角、同旁内角的一对角研究的是三条直线相交的角的情况;
2.同位角、内错角、同旁内角这三类角都是一种位置关系,而不是大小关系;
3.同位角、内错角、同旁内角总是成对出现的;
4.判断“三线八角”中的两个角的位置关系,同位角为“F”形,内错角为“Z”形,同旁内角为“U”形,截线是这些角的边所共有的直线.
5.三线八角
如图所示,将一块三角板镶嵌在两根木棒(AD与AE)之间(木棒可看成是线段),则图中共有 对同旁内角.
4
1.平行线是在同一平面内具有特殊位置关系的两条直线.平行线没有公共点,但没有交点未必就平行,只有在“同一平面内”才平行;
2.平行线指的是“两条直线”,而不是两条线段或射线,若说两条线段(射线)平行,则指的是两条线段(射线)所在的直线平行;
3.“不相交”就是说两条直线没有交点,即没有公共点;
4.平行关系是相互的,若AB∥CD,也可写作CD∥AB;
5.平行公理中的“有”是指存在性,即“经过直线外一点,有一条直线与已知直线平行”,“只有”是指唯一性,即“经过直线外一点,只有一条直线与已知直线平行”.二者缺一不可.
6.平行线的判定及平行公理
7.判断两条直线平行的步骤:先找同位角或内错角,看它们是否相等;若没有,再找同旁内角,看它们是否互补;若还没有,再找题中有无对顶角等可以转换为同位角、内错角或同旁内角;若没有,看两条直线是否平行于第三条直线.
如图所示,已知∠1=∠2,AC平分∠DAB,试说明DC∥AB.
解:因为AC平分∠DAB(已知),
所以∠1=∠CAB(角平分线定义).
又因为∠1=∠2(已知),
所以∠CAB=∠2(等量代换).
所以AB∥CD(内错角相等,两直线平行).
8.平行线的性质
1.平行线的性质与判定的联系与区别.联系:性质与判定的已知和结论正好相反,都是角的关系与平行线相关.区别:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行.
2.同位角相等、同旁内角互补、内错角相等,都是平行线特有的性质,且不可忽略前提条件“两直线平行”,不要看到同位角或内错角,就认为是相等的.
如图所示,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
解:因为EF∥BC,
所以∠BAF=180°-∠B=100°,
因为AC平分∠BAF,
所以∠CAF=∠BAF=50°,
因为EF∥BC,
所以∠C=∠CAF=50°
9.命题,定理。证明
1.必须是对某件事情作出判断的句子,才能叫命题,反之不能作出判断的句子,不叫命题,这是辨别一个语句是否是命题的根本原则.
2.命题的形式并非全部是语言叙述的形式,也可以用数学符号表示.
3.命题的内容并非全部为数学语言,还有生活中其他方面更广泛的内涵.
说出下列命题的题设和结论.
(1)互为邻补角的两个角的平分线互相垂直;
(2)钝角大于它的补角.
(1)题设:两角互为邻补角,结论:它们的平分线互相垂直.
(2)题设:一个角是钝角,结论:这个角大于它的补角.
9.平移
1.平移是图形的基本变换,方向和距离是平移变换的基本要素:平移的方向,它可以是上、下、左、右或用方向角表示;平移的距离就是新图形与原图形对应点连线的长度.
2.平移时图形的所有点移动方向一致,并且移动的距离相等,所以确定一个图形平移的方向和距离,只需确定其中一个点平移的方向和距离.
3.平移与平行有关,平移可以将一个角、一条线段、一个图形平移到另一个位置,使分散的条件集中到一个图形上,便于解决问题.
关于图形平移,下列结论错误的是 ( )A.对应线段相等B.对应角相等C.对应点所连的线段互相平分D.对应点所连的线段相等
c
