2020-2021学年人教版数学七年级下册5.3.2命题、定理、证明课件(44张)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册5.3.2命题、定理、证明课件(44张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 00:00:00 | ||
图片预览











文档简介
(共44张PPT)
人教版 · 数学· 七年级(下)
第5章 相交线与平行线
5.3.2 命题、定理、证明
1.理解命题,定理及证明的概念,会区分命题的题设和结论。
2.会判断真假命题,知道证明的意义及必要性,了解反例的作用。
学习目标
请同学读出下列语句:
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)两条平行线被第三条直线所截,同旁内角互补;
(3)对顶角相等;
(4)等式两边都加同一个数,结果仍是等式.
像这样判断一件事情的语句,叫做命题.
新知一 命题的概念
合作探究
2.如果一个句子没有对某一件事情作出任何判断,那么
它就不是命题.
如:画线段AB=CD.
1.只要对一件事情作出了判断,不管正确与否,都是命题.
如:相等的角是对顶角.
注意:
例 判断下列四个语句中,哪个是命题, 哪个不是命题?并
说明理由:
(1)对顶角相等吗?
(2)画一条线段AB=2cm;
(3)两条直线平行,同位角相等;
(4)相等的两个角,一定是对顶角.
解:(3)(4)是命题,(1)(2)不是命题.
理由如下:(1)是问句,故不是命题;
(2)是做一件事情,也不是命题.
典例精析 命题的识别
下列语句在表述形式上,哪些是命题?哪些不是命题?
(1)对顶角相等;
(2)画一个角等于已知角;
(3)两直线平行,同位角相等;
(4)a、b两条直线平行吗?
(5)温柔的李明明;
(6)玫瑰花是动物;
(7)若a2=4,求a的值;
(8)若a2=b2,则a=b.
否
是
否
否
是
否
是
是
巩固新知
观察下列命题,你能发现这些命题有什么共同的结构特
征?与同伴交流.
(1)如果两个三角形的三条边相等,那么这两个三角形的周长相等;
(2)如果两个数的绝对值相等,那么这两个数也相等;
(3)如果一个数的平方等于9,那么这个数是3.
都是“如果……那么……”的形式.
新知二 命题的构成
合作探究
命题一般都可以写成“如果……那么……”的形式.
1.“如果”后接的部分是题设,
2.“那么”后接的部分是结论.
如命题:熊猫没有翅膀.改写为:
如果这个动物是熊猫,那么它就没有翅膀.
注意:添加“如果”“那么”后,命题的意义不能改变,改写的句子要完整,语句要通顺,使命题的题设和结论更明朗,易于分辨,改写过程中,要适当增加词语,切不可生搬硬套.
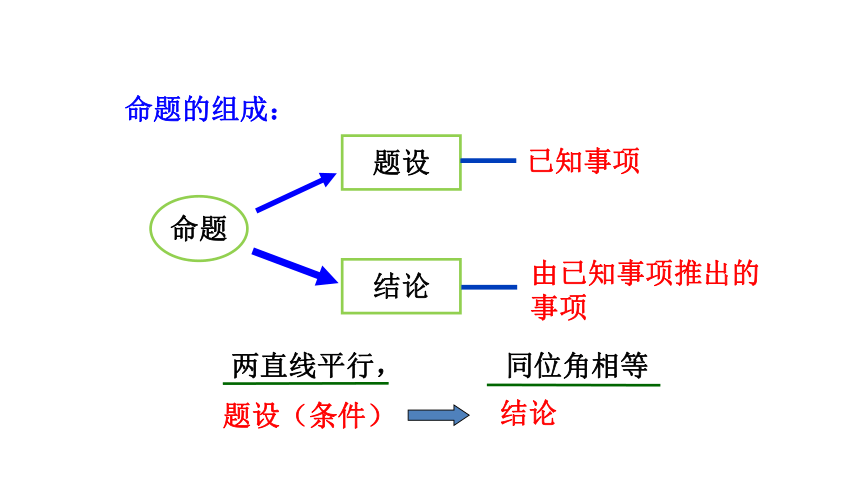
命题
题设
结论
已知事项
由已知事项推出的事项
两直线平行, 同位角相等
题设(条件)
结论
命题的组成:
例 分别把下列命题写成“如果……那么……”的形式.
(1)两点确定一条直线;
(2)等角的补角相等;
(3)内错角相等.
解:(1)如果有两个定点,那么过这两点有且只有一条直线;
(2)如果两个角分别是两个等角的补角,那么这两个角相等;
(3)如果两个角是内错角,那么这两个角相等.
典例精析 命题表述形式的变换
请将它们改写成“如果……,那么……”的形式.
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
(5)对顶角相等.
如果两条直线被第三条直线所截,那么同旁内角互补;
如果等式两边都加同一个数,那么结果仍是等式;
如果两个数互为相反数,那么这两个数相加得0;
如果两个角是同旁内角,那么这两个角互补;
如果两个角互为对顶角,那么这两个角相等.
巩固新知
有些命题如果题设成立,那么结论一定成立;而有些命题题设成立时,结论不一定成立.
正确的命题叫真命题,错误的命题叫假命题.
如命题:“如果两个角互补,那么它们是邻补角”就是一个错误的命题.
如命题:“如果一个数能被4整除,那么它也能被2整除”就是一个正确的命题.
确定一个命题真假的方法:
利用已有的知识,通过观察、验证、推理、举反例等方法.
新知三 真假命题的概念
合作探究
例 下列命题哪些命题是正确的,哪些命题是错误的?
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
(5)对顶角相等.
√
√
√
典例精析 真假命题的识别
×
×
下列句子哪些是命题?是命题的,指出是真命题还是假命题?
(1)猪有四只脚;
(2)内错角相等;
(3)画一条直线;
(4)四边形是正方形;
(5)你的作业做完了吗?
(6)同位角相等,两直线平行;
(7)同角的补角相等;
(8)同垂直于一直线的两直线平行;
(9)过点P画线段MN的垂线;
(10)x>2.
是
真命题
否
是
假命题
是
假命题
否
是
真命题
是
真命题
是
真命题
否
否
巩固新知
“因为早上我发现王五从苹果园那边过来,把一袋东西背回家,还发现我果园的苹果被人偷了,我知道王五家没有苹果树.
所以我家苹果肯定是王五偷的.”
情节1:一天早上,张老汉来到公安局里告状说:王五刚刚在他地里偷了一袋子苹果.文局长立即派干警将王五传唤到公安局审讯:
文局长问张老汉:“你怎知是王五偷了你的苹果 ”
这种从已知条件出发(列出理由),推断出结论的证明方法,叫综合法.综合法是最常用的证明方法.
新知四 证明和反证法(举反例)
张老汉想证明什么?他是怎么证明的?
根据张老汉的证明,你能断定苹果是王五偷的吗?你觉得有疑点吗?
合作探究
情节2:文局长一时拿不定主意,就问旁边的梁副局长:“梁局长,你怎么看?”
梁局长说“这事要证明是王五干的,还得弄清那袋子里装的是不是刚摘的苹果,还要看看地里的脚印是不是王五的才行.
如果袋子里装的是刚摘的苹果,且地里的脚印是王五的,那就一定是他偷的.”
从结论出发,逆着寻找所需要的条件的思考过程,叫分析.
在分析的过程中,如果发现所需要的条件,都已具备或可从已知条件中推得.那么证明就很容易了.
在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程叫作证明.
注意:证明的每一步推理都要有根据,不能“想当然”.
这些根据,可以是已知条件,也可以是学过的定义、
基本事实、定理等.
证明的概念
确定一个命题是假命题的方法:
例如,要判定命题“相等的角是对顶角”是假命题 ,可以举出如下反例:
如图,OC是∠AOB的平分线, ∠1=∠2,但它们不是对顶角.
)
)
1
2
A
O
C
B
只要举出一个例子(反例):它符合命题的题设,但不满足结论即可.
【讨论】如何判定一个命题是假命题呢?
举反例
分析:要证明AB,CD平行,就需要同位角相等的条件,图中∠1与∠3就是同位角.我们只要找到:能说明它们相等的条件就行了.
从图中,我们可以发现:∠2与∠3是对顶角,所以∠3=∠2.这样我们就找到了∠1与∠3相等的确切条件了.
例 如图,∠1=∠2,试说明直线AB,CD平行.
典例精析 利用证明推理解决问题
证明:
∵∠2与∠3是对顶角,
∴∠3=∠2.
又∵∠1=∠2,
∴∠1=∠3.
∴AB∥CD.
B
D
C
E
A
F
1
2
3
如图所示,直线AB和直线CD,直线BE和直线CF都被直线
BC所截,在下面三个式子中,请你选择其中两个作为题设,
剩下的一个作为结论,组成一个真命题并写出对应的推理过程
①AB∥CD,②BE∥CF,③∠1=∠2
题设(已知); .
结论(求证): .
①②
③
巩固新知
理由:
证明:∵AB∥CD,
∠ABC=∠DCB,
又∵BE∥CF.
∴∠EBC=∠FCB.
∵∠ABC-∠EBC=∠DCB-∠FCB,
∴∠1=∠2.
数学中有些命题的正确性是人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据,这样的真命题叫做公理.
两点确定一条直线.
两点间线段最短.
经过直线外的一点有且仅有一条直线与已知直线平行.
直线公理:
线段公理:
平行线公理:
公理的概念
新知五 公理和定理的概念
合作探究
有些命题是基本事实,还有些命题它们的正确性是经过推理证实的,这样得到的真命题叫做定理.定理也可以作为继续推理的依据.
同角或等角的补角相等.
(2)余角的性质:
同角或等角的余角相等.
(4)垂线的性质:
①在同一平面内过一点有且只有一条直线与已知直线垂直;
(1)补角的性质:
(3)对顶角的性质:
对顶角相等.
②垂线段最短.
学过的定理:
定理的概念
例 已知:b∥c, a⊥b .
求证:a⊥c.
证明: ∵ a ⊥b(已知),
∴ ∠1=90°(垂直的定义).
又∵ b ∥ c(已知),
∴ ∠2=∠1=90°(两直线平行,同位角相等).
∴ a ⊥ c(垂直的定义).
a
b
c
1
2
典例精析 利用公理定理进行推理
填空:
已知:如图,∠1=∠2,∠3=∠4,
求证:EG∥FH.
证明:∵∠1=∠2(已知), ∠AEF=∠1 ( ),
∴∠AEF=∠2 ( ).
∴AB∥CD ( ).
∴∠BEF=∠CFE ( ).
∵∠3=∠4(已知),∴∠BEF-∠4=∠CFE-∠3.
即∠GEF=∠HFE ( ).
∴EG∥FH ( ).
对顶角相等
等量代换
同位角相等,两直线平行
两直线平行,内错角相等
等式性质
内错角相等,两直线平行
巩固新知
1.(3分)下列语句,不是命题的是( )
A.两点之间线段最短
B.两直线不平行就相交
C.连接A,B两点
D.对顶角相等
C
课堂练习
2.(4分)“垂直于同一条直线的两条直线互相平行”的
题设是_________________________,结论是________________.
两条直线和同一条直线垂直
这两条直线平行
3.(6分)把下列命题改写成“如果……那么……”的形式.
(1)平行于同一直线的两条直线互相平行;
(2)两点确定一条直线;
(3)同旁内角互补.
解:(1)如果两条直线都平行于同一条直线,那么这两条直线互相平行
(2)如果有两个已知点,那么经过这两个已知点有且只有一条直线
(3)如果两个角是同旁内角,那么这两个角互补
4.(3分)下列命题中,是假命题的是( )
A.内错角相等
B.等角的补角相等
C.能被6整除的数一定能被3整除
D.一个角的余角可以等于它本身
A
A
6.(6分)判断下列命题的真假,是假命题的举出反例.
(1)两个锐角的和是钝角;
(2)一个角的补角大于这个角;
(3)不相等的角不是对顶角.
解:(1)假命题.反例为30°+30°=60°
(2)假命题.反例为120°的补角为60°
(3)真命题
7.(3分)下列说法错误的是( )
A.命题不一定是定理,定理一定是命题
B.定理不可能是假命题
C.真命题是定理
D.如果真命题的正确性是经过推理证实的,那么这样得到的真命题是定理
C
角平分线的定义
55
DAC
等量代换
内错角相等,两直线平行
9.(6分)已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中是真命题的是_________(填写所有真命题的序号),
请你选出一个真命题给出证明.
解:答案不唯一,选择①证明:已知:如图,a∥b,a⊥c,求证:b⊥c.
证明:∵a∥b,∴∠1=∠2.又∵a⊥c,∴∠1=∠2=90°,∴b⊥c
①②④
真命题
假命题
公理
定理
(只需举一个反例)
(不需证明)
(由推理证实)
1.命题的定义:
2.命题的组成:
3.命题的分类:
判断一件事情的句子
题设和结论
归纳新知
1.下列命题中真命题的个数是( )
(1)过一点作已知直线的垂线,有且只有一条;
(2)垂线段最短;
(3)过直线外一点有且只有一条直线与已知直线平行;
(4)垂直于同一直线的两条直线平行;
(5)内错角相等.
A.1 B.2 C.3 D.4
B
课后练习
2.下列命题中,假命题有( )
①若a2=4,则a=2;②若a>b,则a2>b2;
③若a>b,b>c,则a>c;④若a2=b2,则|a|=|b|.
A.1个 B.2个 C.3个 D.4个
3.把“等角的余角相等”改写成“如果……那么……”的形式
是_______________________________________,该命题是____命题.(填“真”或“假”)
B
如果两个角是等角的余角,那么这两个角相等
真
4.对于同一平面内的三条直线a,b,c,给出下列五个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c,以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题:_____________.(用序号写出一个即可)
①② ④
5.如图所示,如果已知∠1=∠2,则AB∥CD,这个命题是真命题吗?若不是,请你再添加一个条件,使该命题成为真命题,并说明理由.
解:是假命题,添加BE∥DF,∵BE∥DF,∴∠EBD=∠FDN.∵∠1=∠2,
∴∠ABD=∠CDN,
∴AB∥CD
6.命题“两直线平行,内错角的平分线互相平行”是真命题吗?如果是,请给出证明;如果不是,请举出反例.
7.如图,有三个论断:①∠1=∠2;②∠B=∠D;③∠A=∠C,请从中任选两个作为条件,另一个作为结论构成一个真命题,并证明该命题的正确性.
解:答案不唯一.如选②∠B=∠D;③∠A=∠C.
求证:①∠1=∠2.
证明:∵∠A=∠C,∴AB∥CD.∴∠B=∠BFC.
∵∠B=∠D,∴∠BFC=∠D.
∴DE∥BF.∴∠DMN=∠BNM.
∵∠1=∠DMN,∠2=∠BNM,
∴∠1=∠2
8.阅读以下两题后作出相应的解答:
(1)“同位角相等,两直线平行”,“两直线平行,同位角相等”,这两个命题的题设和结论在命题中的位置恰好对调,我们把其中一命题叫做另一个命题的逆命题,请你写出命题“角平分线上的点到角两边的距离相等”的逆命题,并指出逆命题的题设和结论;
(2)根据以下语句作出图形,并写出该命题的文字表述.
已知:过直线AB上一点O任作射线OC,OM,ON分别平分∠AOC,
∠BOC,则OM⊥ON.
解:(1)逆命题:在角的内部到角两边距离相等的点
在这个角的平分线上 题设:在角的内部到角两边距离相等的点
结论:这个点在这个角的平分线上
(2)图略,邻补角的角平分线互相垂直
再见
人教版 · 数学· 七年级(下)
第5章 相交线与平行线
5.3.2 命题、定理、证明
1.理解命题,定理及证明的概念,会区分命题的题设和结论。
2.会判断真假命题,知道证明的意义及必要性,了解反例的作用。
学习目标
请同学读出下列语句:
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)两条平行线被第三条直线所截,同旁内角互补;
(3)对顶角相等;
(4)等式两边都加同一个数,结果仍是等式.
像这样判断一件事情的语句,叫做命题.
新知一 命题的概念
合作探究
2.如果一个句子没有对某一件事情作出任何判断,那么
它就不是命题.
如:画线段AB=CD.
1.只要对一件事情作出了判断,不管正确与否,都是命题.
如:相等的角是对顶角.
注意:
例 判断下列四个语句中,哪个是命题, 哪个不是命题?并
说明理由:
(1)对顶角相等吗?
(2)画一条线段AB=2cm;
(3)两条直线平行,同位角相等;
(4)相等的两个角,一定是对顶角.
解:(3)(4)是命题,(1)(2)不是命题.
理由如下:(1)是问句,故不是命题;
(2)是做一件事情,也不是命题.
典例精析 命题的识别
下列语句在表述形式上,哪些是命题?哪些不是命题?
(1)对顶角相等;
(2)画一个角等于已知角;
(3)两直线平行,同位角相等;
(4)a、b两条直线平行吗?
(5)温柔的李明明;
(6)玫瑰花是动物;
(7)若a2=4,求a的值;
(8)若a2=b2,则a=b.
否
是
否
否
是
否
是
是
巩固新知
观察下列命题,你能发现这些命题有什么共同的结构特
征?与同伴交流.
(1)如果两个三角形的三条边相等,那么这两个三角形的周长相等;
(2)如果两个数的绝对值相等,那么这两个数也相等;
(3)如果一个数的平方等于9,那么这个数是3.
都是“如果……那么……”的形式.
新知二 命题的构成
合作探究
命题一般都可以写成“如果……那么……”的形式.
1.“如果”后接的部分是题设,
2.“那么”后接的部分是结论.
如命题:熊猫没有翅膀.改写为:
如果这个动物是熊猫,那么它就没有翅膀.
注意:添加“如果”“那么”后,命题的意义不能改变,改写的句子要完整,语句要通顺,使命题的题设和结论更明朗,易于分辨,改写过程中,要适当增加词语,切不可生搬硬套.
命题
题设
结论
已知事项
由已知事项推出的事项
两直线平行, 同位角相等
题设(条件)
结论
命题的组成:
例 分别把下列命题写成“如果……那么……”的形式.
(1)两点确定一条直线;
(2)等角的补角相等;
(3)内错角相等.
解:(1)如果有两个定点,那么过这两点有且只有一条直线;
(2)如果两个角分别是两个等角的补角,那么这两个角相等;
(3)如果两个角是内错角,那么这两个角相等.
典例精析 命题表述形式的变换
请将它们改写成“如果……,那么……”的形式.
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
(5)对顶角相等.
如果两条直线被第三条直线所截,那么同旁内角互补;
如果等式两边都加同一个数,那么结果仍是等式;
如果两个数互为相反数,那么这两个数相加得0;
如果两个角是同旁内角,那么这两个角互补;
如果两个角互为对顶角,那么这两个角相等.
巩固新知
有些命题如果题设成立,那么结论一定成立;而有些命题题设成立时,结论不一定成立.
正确的命题叫真命题,错误的命题叫假命题.
如命题:“如果两个角互补,那么它们是邻补角”就是一个错误的命题.
如命题:“如果一个数能被4整除,那么它也能被2整除”就是一个正确的命题.
确定一个命题真假的方法:
利用已有的知识,通过观察、验证、推理、举反例等方法.
新知三 真假命题的概念
合作探究
例 下列命题哪些命题是正确的,哪些命题是错误的?
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
(5)对顶角相等.
√
√
√
典例精析 真假命题的识别
×
×
下列句子哪些是命题?是命题的,指出是真命题还是假命题?
(1)猪有四只脚;
(2)内错角相等;
(3)画一条直线;
(4)四边形是正方形;
(5)你的作业做完了吗?
(6)同位角相等,两直线平行;
(7)同角的补角相等;
(8)同垂直于一直线的两直线平行;
(9)过点P画线段MN的垂线;
(10)x>2.
是
真命题
否
是
假命题
是
假命题
否
是
真命题
是
真命题
是
真命题
否
否
巩固新知
“因为早上我发现王五从苹果园那边过来,把一袋东西背回家,还发现我果园的苹果被人偷了,我知道王五家没有苹果树.
所以我家苹果肯定是王五偷的.”
情节1:一天早上,张老汉来到公安局里告状说:王五刚刚在他地里偷了一袋子苹果.文局长立即派干警将王五传唤到公安局审讯:
文局长问张老汉:“你怎知是王五偷了你的苹果 ”
这种从已知条件出发(列出理由),推断出结论的证明方法,叫综合法.综合法是最常用的证明方法.
新知四 证明和反证法(举反例)
张老汉想证明什么?他是怎么证明的?
根据张老汉的证明,你能断定苹果是王五偷的吗?你觉得有疑点吗?
合作探究
情节2:文局长一时拿不定主意,就问旁边的梁副局长:“梁局长,你怎么看?”
梁局长说“这事要证明是王五干的,还得弄清那袋子里装的是不是刚摘的苹果,还要看看地里的脚印是不是王五的才行.
如果袋子里装的是刚摘的苹果,且地里的脚印是王五的,那就一定是他偷的.”
从结论出发,逆着寻找所需要的条件的思考过程,叫分析.
在分析的过程中,如果发现所需要的条件,都已具备或可从已知条件中推得.那么证明就很容易了.
在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程叫作证明.
注意:证明的每一步推理都要有根据,不能“想当然”.
这些根据,可以是已知条件,也可以是学过的定义、
基本事实、定理等.
证明的概念
确定一个命题是假命题的方法:
例如,要判定命题“相等的角是对顶角”是假命题 ,可以举出如下反例:
如图,OC是∠AOB的平分线, ∠1=∠2,但它们不是对顶角.
)
)
1
2
A
O
C
B
只要举出一个例子(反例):它符合命题的题设,但不满足结论即可.
【讨论】如何判定一个命题是假命题呢?
举反例
分析:要证明AB,CD平行,就需要同位角相等的条件,图中∠1与∠3就是同位角.我们只要找到:能说明它们相等的条件就行了.
从图中,我们可以发现:∠2与∠3是对顶角,所以∠3=∠2.这样我们就找到了∠1与∠3相等的确切条件了.
例 如图,∠1=∠2,试说明直线AB,CD平行.
典例精析 利用证明推理解决问题
证明:
∵∠2与∠3是对顶角,
∴∠3=∠2.
又∵∠1=∠2,
∴∠1=∠3.
∴AB∥CD.
B
D
C
E
A
F
1
2
3
如图所示,直线AB和直线CD,直线BE和直线CF都被直线
BC所截,在下面三个式子中,请你选择其中两个作为题设,
剩下的一个作为结论,组成一个真命题并写出对应的推理过程
①AB∥CD,②BE∥CF,③∠1=∠2
题设(已知); .
结论(求证): .
①②
③
巩固新知
理由:
证明:∵AB∥CD,
∠ABC=∠DCB,
又∵BE∥CF.
∴∠EBC=∠FCB.
∵∠ABC-∠EBC=∠DCB-∠FCB,
∴∠1=∠2.
数学中有些命题的正确性是人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据,这样的真命题叫做公理.
两点确定一条直线.
两点间线段最短.
经过直线外的一点有且仅有一条直线与已知直线平行.
直线公理:
线段公理:
平行线公理:
公理的概念
新知五 公理和定理的概念
合作探究
有些命题是基本事实,还有些命题它们的正确性是经过推理证实的,这样得到的真命题叫做定理.定理也可以作为继续推理的依据.
同角或等角的补角相等.
(2)余角的性质:
同角或等角的余角相等.
(4)垂线的性质:
①在同一平面内过一点有且只有一条直线与已知直线垂直;
(1)补角的性质:
(3)对顶角的性质:
对顶角相等.
②垂线段最短.
学过的定理:
定理的概念
例 已知:b∥c, a⊥b .
求证:a⊥c.
证明: ∵ a ⊥b(已知),
∴ ∠1=90°(垂直的定义).
又∵ b ∥ c(已知),
∴ ∠2=∠1=90°(两直线平行,同位角相等).
∴ a ⊥ c(垂直的定义).
a
b
c
1
2
典例精析 利用公理定理进行推理
填空:
已知:如图,∠1=∠2,∠3=∠4,
求证:EG∥FH.
证明:∵∠1=∠2(已知), ∠AEF=∠1 ( ),
∴∠AEF=∠2 ( ).
∴AB∥CD ( ).
∴∠BEF=∠CFE ( ).
∵∠3=∠4(已知),∴∠BEF-∠4=∠CFE-∠3.
即∠GEF=∠HFE ( ).
∴EG∥FH ( ).
对顶角相等
等量代换
同位角相等,两直线平行
两直线平行,内错角相等
等式性质
内错角相等,两直线平行
巩固新知
1.(3分)下列语句,不是命题的是( )
A.两点之间线段最短
B.两直线不平行就相交
C.连接A,B两点
D.对顶角相等
C
课堂练习
2.(4分)“垂直于同一条直线的两条直线互相平行”的
题设是_________________________,结论是________________.
两条直线和同一条直线垂直
这两条直线平行
3.(6分)把下列命题改写成“如果……那么……”的形式.
(1)平行于同一直线的两条直线互相平行;
(2)两点确定一条直线;
(3)同旁内角互补.
解:(1)如果两条直线都平行于同一条直线,那么这两条直线互相平行
(2)如果有两个已知点,那么经过这两个已知点有且只有一条直线
(3)如果两个角是同旁内角,那么这两个角互补
4.(3分)下列命题中,是假命题的是( )
A.内错角相等
B.等角的补角相等
C.能被6整除的数一定能被3整除
D.一个角的余角可以等于它本身
A
A
6.(6分)判断下列命题的真假,是假命题的举出反例.
(1)两个锐角的和是钝角;
(2)一个角的补角大于这个角;
(3)不相等的角不是对顶角.
解:(1)假命题.反例为30°+30°=60°
(2)假命题.反例为120°的补角为60°
(3)真命题
7.(3分)下列说法错误的是( )
A.命题不一定是定理,定理一定是命题
B.定理不可能是假命题
C.真命题是定理
D.如果真命题的正确性是经过推理证实的,那么这样得到的真命题是定理
C
角平分线的定义
55
DAC
等量代换
内错角相等,两直线平行
9.(6分)已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中是真命题的是_________(填写所有真命题的序号),
请你选出一个真命题给出证明.
解:答案不唯一,选择①证明:已知:如图,a∥b,a⊥c,求证:b⊥c.
证明:∵a∥b,∴∠1=∠2.又∵a⊥c,∴∠1=∠2=90°,∴b⊥c
①②④
真命题
假命题
公理
定理
(只需举一个反例)
(不需证明)
(由推理证实)
1.命题的定义:
2.命题的组成:
3.命题的分类:
判断一件事情的句子
题设和结论
归纳新知
1.下列命题中真命题的个数是( )
(1)过一点作已知直线的垂线,有且只有一条;
(2)垂线段最短;
(3)过直线外一点有且只有一条直线与已知直线平行;
(4)垂直于同一直线的两条直线平行;
(5)内错角相等.
A.1 B.2 C.3 D.4
B
课后练习
2.下列命题中,假命题有( )
①若a2=4,则a=2;②若a>b,则a2>b2;
③若a>b,b>c,则a>c;④若a2=b2,则|a|=|b|.
A.1个 B.2个 C.3个 D.4个
3.把“等角的余角相等”改写成“如果……那么……”的形式
是_______________________________________,该命题是____命题.(填“真”或“假”)
B
如果两个角是等角的余角,那么这两个角相等
真
4.对于同一平面内的三条直线a,b,c,给出下列五个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c,以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题:_____________.(用序号写出一个即可)
①② ④
5.如图所示,如果已知∠1=∠2,则AB∥CD,这个命题是真命题吗?若不是,请你再添加一个条件,使该命题成为真命题,并说明理由.
解:是假命题,添加BE∥DF,∵BE∥DF,∴∠EBD=∠FDN.∵∠1=∠2,
∴∠ABD=∠CDN,
∴AB∥CD
6.命题“两直线平行,内错角的平分线互相平行”是真命题吗?如果是,请给出证明;如果不是,请举出反例.
7.如图,有三个论断:①∠1=∠2;②∠B=∠D;③∠A=∠C,请从中任选两个作为条件,另一个作为结论构成一个真命题,并证明该命题的正确性.
解:答案不唯一.如选②∠B=∠D;③∠A=∠C.
求证:①∠1=∠2.
证明:∵∠A=∠C,∴AB∥CD.∴∠B=∠BFC.
∵∠B=∠D,∴∠BFC=∠D.
∴DE∥BF.∴∠DMN=∠BNM.
∵∠1=∠DMN,∠2=∠BNM,
∴∠1=∠2
8.阅读以下两题后作出相应的解答:
(1)“同位角相等,两直线平行”,“两直线平行,同位角相等”,这两个命题的题设和结论在命题中的位置恰好对调,我们把其中一命题叫做另一个命题的逆命题,请你写出命题“角平分线上的点到角两边的距离相等”的逆命题,并指出逆命题的题设和结论;
(2)根据以下语句作出图形,并写出该命题的文字表述.
已知:过直线AB上一点O任作射线OC,OM,ON分别平分∠AOC,
∠BOC,则OM⊥ON.
解:(1)逆命题:在角的内部到角两边距离相等的点
在这个角的平分线上 题设:在角的内部到角两边距离相等的点
结论:这个点在这个角的平分线上
(2)图略,邻补角的角平分线互相垂直
再见
