5.2.2平行线的判定 课件(共35张PPT)
文档属性
| 名称 | 5.2.2平行线的判定 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 950.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 18:46:05 | ||
图片预览






文档简介
(共35张PPT)
平行线的判定
七年级下册
1、能根据“同位角相等,两直线平行”证明“同旁内角互补,两直线平行”“内错角相等,两直线平行”,并能简单地应用这些结论.
2、初步了解证明的基本步骤和书写格式.
3、体会几何中推理的严谨性、书写的规范性,发展初步的演绎推理能力.
1.下列说法:①用两根钉子固定一根木条,体现数学事实是两点之间线段最短;②射线AB与射线BA表示同一条射线;③若AB=BC,则B为线段AC的中点;④不相交的两条直线叫做平行线;⑤过一点有且只有一条直线与已知直线垂直,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2. 下列说法中,正确的是( )
A.两条不相交的直线叫做平行线
B.一条直线的平行线有且只有一条
C.在同一平面内,若直线a∥b,a∥c,则b∥c
D.若两条线段不相交,则它们互相平行
B
C
3. 给出下列判断:①两条不相交的直线叫做平行线;②不相等的两个角一定不是对顶角;③若两个角的一边在同一直线上,另一对边互相平行,则这两个角相等;④如果两个角是邻补角,那么这两个角的平分线组成的图形是直角,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
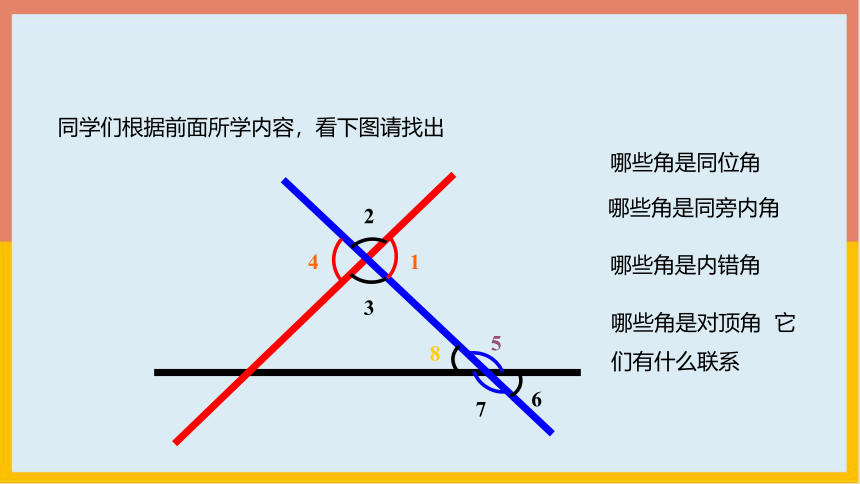
同学们根据前面所学内容,看下图请找出
哪些角是内错角
哪些角是同位角
哪些角是同旁内角
哪些角是对顶角 它们有什么联系
2
3
4
1
5
7
8
6
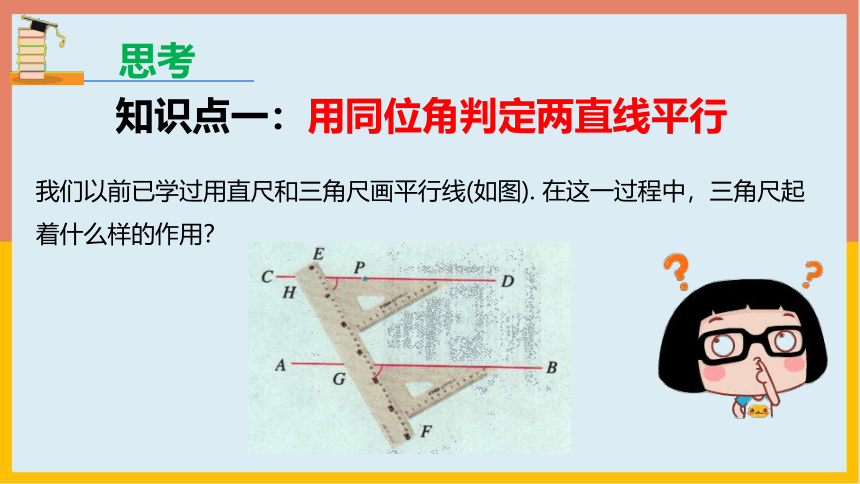
我们以前已学过用直尺和三角尺画平行线(如图). 在这一过程中,三角尺起着什么样的作用?
思考
知识点一:用同位角判定两直线平行
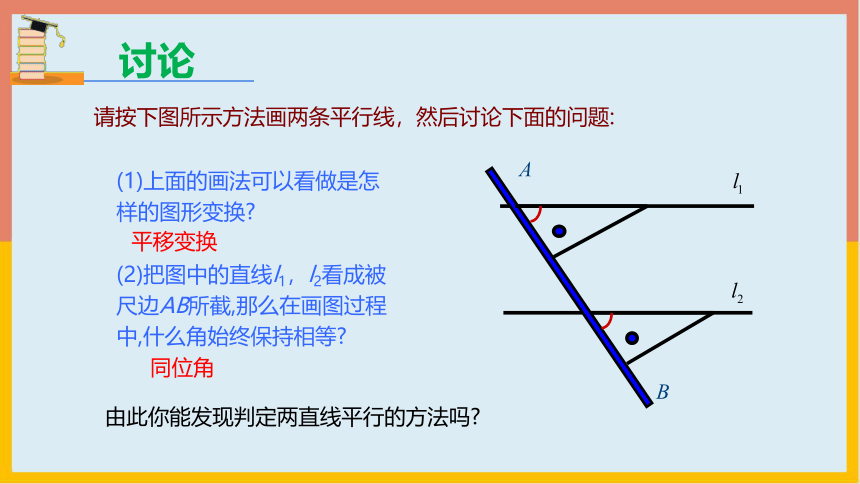
请按下图所示方法画两条平行线,然后讨论下面的问题:
(1)上面的画法可以看做是怎样的图形变换
(2)把图中的直线l1,l2看成被尺边AB所截,那么在画图过程中,什么角始终保持相等
平移变换
同位角
由此你能发现判定两直线平行的方法吗
讨论
公理 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行
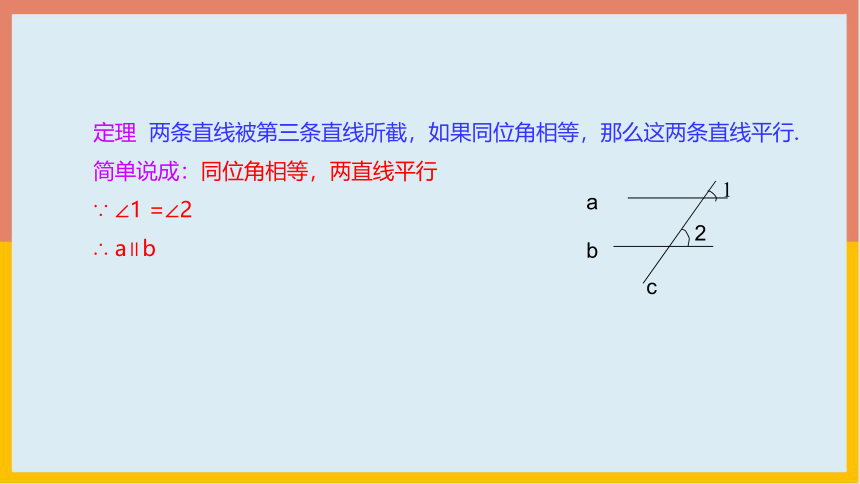
定理 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行
∵ ∠1 =∠2
∴ a∥b
1
a
b
c
2
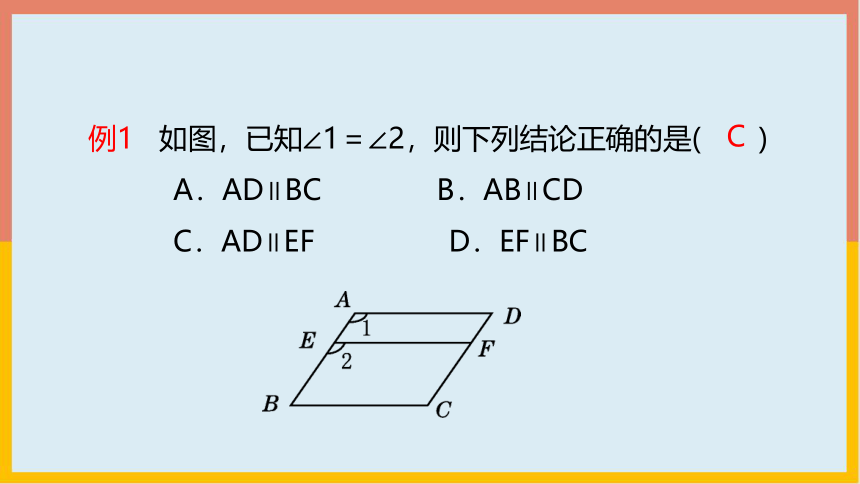
例1 如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
C
利用同位角相等来判定两直线平行的方法:
首先要找出这对同位角是哪两条直线被第三条直线所截形成的;再根据“同位角相等,两直线平行”推导出这两条直线平行.
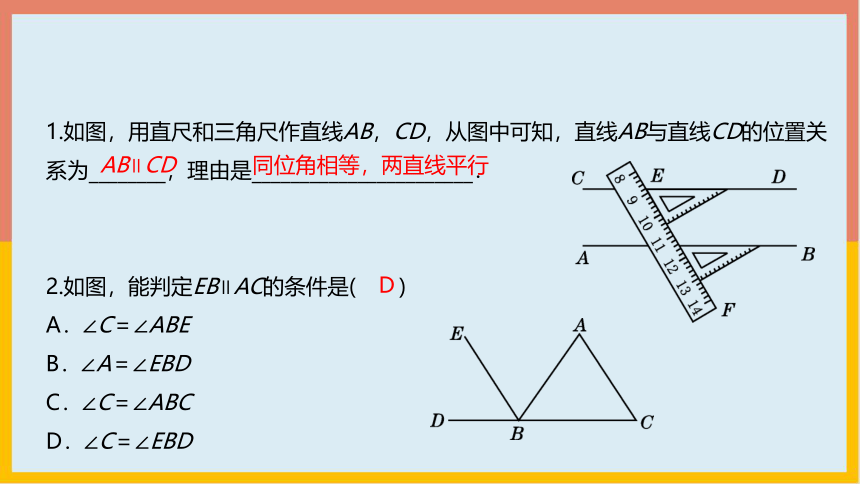
1.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为________,理由是_______________________.
2.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠C=∠EBD
AB∥CD
同位角相等,两直线平行
D
猜想: 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
可以简单说成:内错角相等,两直线平行.
你能运用所学知识来证实它是一个真命题吗
知识点二:用内错角判定两直线平行
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.求证:a∥b.
证明:∵∠1=∠2 (已知),
∠1+∠3=180°(平角的定义).
∴∠2+∠3 = 180°(等量代换).
∴∠2与∠3互补(互补的意义).
∴ a∥b(同旁内角互补,两直线平行).
把你所悟到的证明一个命题的方法,步骤,书写格式以及注意事项内化为一种方法.
借助“同位角相等,两直线平行”这一公理,你还能证明哪些熟悉的结论
a
b
c
1
3
2
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行
∵ ∠1= ∠2
∴ a∥b
1
a
b
c
2
例2 如图,已知∠ADE=60°,DF平分∠ADE,∠1=30°,试说明:DF∥BE.
解:∵DF平分∠ADE(已知),
∴∠EDF= ∠ADE(角平分线的定义).
又∵∠ADE=60°,
∴∠EDF=30°.
又∵∠1=30°(已知),
∴∠EDF=∠1,
∴DF∥BE(内错角相等,两直线平行).
利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
1.如图,BE是AB的延长线.
(1)由∠CBE= ∠A 可以判定哪两条直线平行? 根据是什么?
(2)由∠CBE= ∠C可以判定哪两条直线平行? 根据是什么?
解:(1)由∠CBE=∠A可以判定AD∥BC. 根据是:同位角相等,两直线平行.
(2)由∠CBE=∠C可以判定AB∥CD. 根据是:内错角相等,两直线平行
2.如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2 B.∠2=∠3
C.∠3=∠4 D.∠4=∠5
3.如图,若∠1与∠2互补,∠2与∠4互补,则( )
A.l4∥l5
B.l1∥l2
C.l1∥l3
D.l2∥l3
D
C
思考:你认为“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题正确吗?说明理由.
思考
知识点三:用同旁内角判定两直线平行
a
b
c
1
3
2
已知:如图,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b
证明:∵ ∠1与∠2互补 (已知),
∴∠1+∠2=180°(互补的定义).
∴∠1= 180°-∠2(等式的性质).
又∵∠3+∠2=180° (平角的定义),
∴∠3= 180°-∠2(等式的性质).
∴∠1=∠3(等量代换).
∴ a∥b(同位角相等,两直线平行).
已给的公理,定义和定理以后都可以作为依据,用来证明新的命题.
说说你所悟到的证明一个命题的方法,步骤,书写格式以及注意事项.
定理 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行
∵ ∠1+ ∠2=180°
∴ a∥b
1
a
b
c
2
a
b
c
1
2
公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
同旁内角互补,两直线平行.
∵∠1+∠2=180°, ∴ a∥b.
平行线的判定方法
a
b
c
2
1
a
b
c
1
2
例3 如图,直线AE,CD相交于点O,如果∠A=110°,∠1=70°,就可以说明AB∥CD,这是为什么?
解:因为∠1=∠AOD(对顶角相等),∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD(同旁内角互补,两直线平行).
例4 在同一平面内,如果两条直线都垂直于同 一条直线,那么这两条直线平行吗?为什么?
解:这两条直线平行. 理由如下:
如图.
∵a⊥b,
∴∠1=90°.
同理∠2=90°.
∴∠1=∠2 .
∵ ∠1和∠2 是同位角,
∴b∥c (同位角相等,两直线平行).
判断两条直线是否平行,可以找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行.
判定两直线平行的方法:
方法一:平行线的定义:在同一平面内,不相交的两
条直线就是平行线.
方法二:如果两条直线都和第三条直线平行,那么这
两条直线也互相平行.
方法三:同位角相等,两直线平行.
方法四:内错角相等,两直线平行.
方法五:同旁内角互补,两直线平行.
方法六:在同一平面内,垂直于同一条直线的两条直
线平行.
1. 下列说法中不正确的有( )
①两条不相交的直线叫做平行线;
②经过一点,有且只有一条直线与已知直线垂直;
③经过一点,有且只有一条直线与已知直线平行;
④一个角的两边与另一个角两边互相垂直,那么这两个角相等.
A.1个 B.2个 C.3个 D.4个
2. 已知在同一平面内有三条不同的直线a,b,c,下列说法错误的是( )
A.如果a∥b,a⊥c,那么b⊥c B.如果b∥a,c∥a,那么b∥c
C.如果b⊥a,c⊥a,那么b⊥c D.如果b⊥a,c⊥a,那么b∥c
C
C
3. 平面内有三条直线a、b、c,下列说法:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c,其中正确的是( )
A.只有① B.只有② C.①②都正确 D.①②都不正确
4、 如图,点在延长线上,下列条件中不能判定BD∥AC的是( )
A.∠1=∠2 B.∠3=∠4 C.∠5=∠C D.∠C+∠BDC=180°
5、 如图,下列说法中,正确的是( )
A.若∠3=∠8,则AB∥CD
B.若∠1=∠5,则AB∥CD
C.若∠DAB+∠ABC=180°,则AB∥CD
D.若∠2=∠6,则AB∥CD
A
B
D
6、如图,平行直线AB、CD与相交直线EF、GH相交,图中的同旁内角共有( )
A.4对 B.8对 C.12对 D.16对
7、如图,若直线a,b分别与直线c,d相交,且∠1+∠3=90°,∠2﹣∠3=90°,∠4=115°,那么∠3=___________.
D
65°
8、如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°
求证:AB∥EF.
解:过C点作CG∥AB,过点D作DH∥AB,则CG∥DH,
∵∠B=25°,∴∠BCG=25°,
∵∠BCD=45°,∴∠GCD=20°,
∵CG∥HD,∴∠CDH=20°,
∵∠CDE=30°,∴∠HDE=10°∴∠HDE=∠E=10°,
∴DH∥EF,∴DH∥AB,∴AB∥EF.
9、如图,直线MN和直线AB,CD,EF分别交于点G,H,P,∠1=∠2,∠2+∠3=180°,试问:AB与EF平行吗?为什么?
解:平行.
因为∠1=∠2,∠1=∠BGH,
所以∠2=∠BGH(等量代换),
所以AB∥CD(同位角相等,两直线平行).
所以∠2+∠3=180°,∠3=∠HPF,
所以∠2+∠HPF =180°(等量代换).
所以CD∥EF(同旁内角互补,两直线平行).
所以AB∥EF(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行).
通过本课时的学习,需要我们掌握:
1.两条直线被第三条直线所截,会产生同位角、内错角、同旁内角.角的关系决定了两条直线是否平行,因此在做题时要掌握好“三线八角”;
2.平行线的判定:
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补两直线平行.
1、完成课后习题
再见
平行线的判定
七年级下册
1、能根据“同位角相等,两直线平行”证明“同旁内角互补,两直线平行”“内错角相等,两直线平行”,并能简单地应用这些结论.
2、初步了解证明的基本步骤和书写格式.
3、体会几何中推理的严谨性、书写的规范性,发展初步的演绎推理能力.
1.下列说法:①用两根钉子固定一根木条,体现数学事实是两点之间线段最短;②射线AB与射线BA表示同一条射线;③若AB=BC,则B为线段AC的中点;④不相交的两条直线叫做平行线;⑤过一点有且只有一条直线与已知直线垂直,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2. 下列说法中,正确的是( )
A.两条不相交的直线叫做平行线
B.一条直线的平行线有且只有一条
C.在同一平面内,若直线a∥b,a∥c,则b∥c
D.若两条线段不相交,则它们互相平行
B
C
3. 给出下列判断:①两条不相交的直线叫做平行线;②不相等的两个角一定不是对顶角;③若两个角的一边在同一直线上,另一对边互相平行,则这两个角相等;④如果两个角是邻补角,那么这两个角的平分线组成的图形是直角,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
同学们根据前面所学内容,看下图请找出
哪些角是内错角
哪些角是同位角
哪些角是同旁内角
哪些角是对顶角 它们有什么联系
2
3
4
1
5
7
8
6
我们以前已学过用直尺和三角尺画平行线(如图). 在这一过程中,三角尺起着什么样的作用?
思考
知识点一:用同位角判定两直线平行
请按下图所示方法画两条平行线,然后讨论下面的问题:
(1)上面的画法可以看做是怎样的图形变换
(2)把图中的直线l1,l2看成被尺边AB所截,那么在画图过程中,什么角始终保持相等
平移变换
同位角
由此你能发现判定两直线平行的方法吗
讨论
公理 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行
定理 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行
∵ ∠1 =∠2
∴ a∥b
1
a
b
c
2
例1 如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
C
利用同位角相等来判定两直线平行的方法:
首先要找出这对同位角是哪两条直线被第三条直线所截形成的;再根据“同位角相等,两直线平行”推导出这两条直线平行.
1.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为________,理由是_______________________.
2.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠C=∠EBD
AB∥CD
同位角相等,两直线平行
D
猜想: 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
可以简单说成:内错角相等,两直线平行.
你能运用所学知识来证实它是一个真命题吗
知识点二:用内错角判定两直线平行
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.求证:a∥b.
证明:∵∠1=∠2 (已知),
∠1+∠3=180°(平角的定义).
∴∠2+∠3 = 180°(等量代换).
∴∠2与∠3互补(互补的意义).
∴ a∥b(同旁内角互补,两直线平行).
把你所悟到的证明一个命题的方法,步骤,书写格式以及注意事项内化为一种方法.
借助“同位角相等,两直线平行”这一公理,你还能证明哪些熟悉的结论
a
b
c
1
3
2
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行
∵ ∠1= ∠2
∴ a∥b
1
a
b
c
2
例2 如图,已知∠ADE=60°,DF平分∠ADE,∠1=30°,试说明:DF∥BE.
解:∵DF平分∠ADE(已知),
∴∠EDF= ∠ADE(角平分线的定义).
又∵∠ADE=60°,
∴∠EDF=30°.
又∵∠1=30°(已知),
∴∠EDF=∠1,
∴DF∥BE(内错角相等,两直线平行).
利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
1.如图,BE是AB的延长线.
(1)由∠CBE= ∠A 可以判定哪两条直线平行? 根据是什么?
(2)由∠CBE= ∠C可以判定哪两条直线平行? 根据是什么?
解:(1)由∠CBE=∠A可以判定AD∥BC. 根据是:同位角相等,两直线平行.
(2)由∠CBE=∠C可以判定AB∥CD. 根据是:内错角相等,两直线平行
2.如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2 B.∠2=∠3
C.∠3=∠4 D.∠4=∠5
3.如图,若∠1与∠2互补,∠2与∠4互补,则( )
A.l4∥l5
B.l1∥l2
C.l1∥l3
D.l2∥l3
D
C
思考:你认为“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题正确吗?说明理由.
思考
知识点三:用同旁内角判定两直线平行
a
b
c
1
3
2
已知:如图,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b
证明:∵ ∠1与∠2互补 (已知),
∴∠1+∠2=180°(互补的定义).
∴∠1= 180°-∠2(等式的性质).
又∵∠3+∠2=180° (平角的定义),
∴∠3= 180°-∠2(等式的性质).
∴∠1=∠3(等量代换).
∴ a∥b(同位角相等,两直线平行).
已给的公理,定义和定理以后都可以作为依据,用来证明新的命题.
说说你所悟到的证明一个命题的方法,步骤,书写格式以及注意事项.
定理 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行
∵ ∠1+ ∠2=180°
∴ a∥b
1
a
b
c
2
a
b
c
1
2
公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
同旁内角互补,两直线平行.
∵∠1+∠2=180°, ∴ a∥b.
平行线的判定方法
a
b
c
2
1
a
b
c
1
2
例3 如图,直线AE,CD相交于点O,如果∠A=110°,∠1=70°,就可以说明AB∥CD,这是为什么?
解:因为∠1=∠AOD(对顶角相等),∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD(同旁内角互补,两直线平行).
例4 在同一平面内,如果两条直线都垂直于同 一条直线,那么这两条直线平行吗?为什么?
解:这两条直线平行. 理由如下:
如图.
∵a⊥b,
∴∠1=90°.
同理∠2=90°.
∴∠1=∠2 .
∵ ∠1和∠2 是同位角,
∴b∥c (同位角相等,两直线平行).
判断两条直线是否平行,可以找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行.
判定两直线平行的方法:
方法一:平行线的定义:在同一平面内,不相交的两
条直线就是平行线.
方法二:如果两条直线都和第三条直线平行,那么这
两条直线也互相平行.
方法三:同位角相等,两直线平行.
方法四:内错角相等,两直线平行.
方法五:同旁内角互补,两直线平行.
方法六:在同一平面内,垂直于同一条直线的两条直
线平行.
1. 下列说法中不正确的有( )
①两条不相交的直线叫做平行线;
②经过一点,有且只有一条直线与已知直线垂直;
③经过一点,有且只有一条直线与已知直线平行;
④一个角的两边与另一个角两边互相垂直,那么这两个角相等.
A.1个 B.2个 C.3个 D.4个
2. 已知在同一平面内有三条不同的直线a,b,c,下列说法错误的是( )
A.如果a∥b,a⊥c,那么b⊥c B.如果b∥a,c∥a,那么b∥c
C.如果b⊥a,c⊥a,那么b⊥c D.如果b⊥a,c⊥a,那么b∥c
C
C
3. 平面内有三条直线a、b、c,下列说法:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c,其中正确的是( )
A.只有① B.只有② C.①②都正确 D.①②都不正确
4、 如图,点在延长线上,下列条件中不能判定BD∥AC的是( )
A.∠1=∠2 B.∠3=∠4 C.∠5=∠C D.∠C+∠BDC=180°
5、 如图,下列说法中,正确的是( )
A.若∠3=∠8,则AB∥CD
B.若∠1=∠5,则AB∥CD
C.若∠DAB+∠ABC=180°,则AB∥CD
D.若∠2=∠6,则AB∥CD
A
B
D
6、如图,平行直线AB、CD与相交直线EF、GH相交,图中的同旁内角共有( )
A.4对 B.8对 C.12对 D.16对
7、如图,若直线a,b分别与直线c,d相交,且∠1+∠3=90°,∠2﹣∠3=90°,∠4=115°,那么∠3=___________.
D
65°
8、如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°
求证:AB∥EF.
解:过C点作CG∥AB,过点D作DH∥AB,则CG∥DH,
∵∠B=25°,∴∠BCG=25°,
∵∠BCD=45°,∴∠GCD=20°,
∵CG∥HD,∴∠CDH=20°,
∵∠CDE=30°,∴∠HDE=10°∴∠HDE=∠E=10°,
∴DH∥EF,∴DH∥AB,∴AB∥EF.
9、如图,直线MN和直线AB,CD,EF分别交于点G,H,P,∠1=∠2,∠2+∠3=180°,试问:AB与EF平行吗?为什么?
解:平行.
因为∠1=∠2,∠1=∠BGH,
所以∠2=∠BGH(等量代换),
所以AB∥CD(同位角相等,两直线平行).
所以∠2+∠3=180°,∠3=∠HPF,
所以∠2+∠HPF =180°(等量代换).
所以CD∥EF(同旁内角互补,两直线平行).
所以AB∥EF(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行).
通过本课时的学习,需要我们掌握:
1.两条直线被第三条直线所截,会产生同位角、内错角、同旁内角.角的关系决定了两条直线是否平行,因此在做题时要掌握好“三线八角”;
2.平行线的判定:
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补两直线平行.
1、完成课后习题
再见
