【专练】5.3平行线的判定与性质 专练(含答案)
文档属性
| 名称 | 【专练】5.3平行线的判定与性质 专练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 256.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 11:20:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版七年级数学下册专练
平行线的判定与性质
一.选择题
1.(2021 鞍山一模)如图,∠1=∠2=∠3=56°,则∠4的度数是( )
A.56° B.114° C.124° D.146°
2.(2021 雁塔区校级模拟)如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=( )
A.36° B.52° C.72° D.80°
3.(2021春 单县期末)如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个
C.1个 D.0个
4.(2021春 德宏州期末)如图所示,AC⊥BC,DC⊥EC,则下列结论:①∠1=∠3;②∠ACE+∠2=180°;③若∠A=∠2,则有AB∥CE;④若∠2=∠E,则有∠4=∠A.其中正确的有( )
A.①②③ B.①②④
C.③④ D.①②③④
5.(2021春 汉川市期末)如图,AD∥BC,∠B=∠D,延长BA至点E,连接CE,∠EAD和∠ECD的角平分线交于点P.下列三个结论:①AB∥CD;②∠AOC∠EAD+∠ECD;③若∠E=60°,∠APC=70°,则∠D=80°.其中结论正确的个数有( )
A.0 B.1
C.2 D.3
二.填空题
6.(2021春 夏津县期末)如图,CB平分∠ACD,∠2=∠3,若∠4=60°,则∠5的度数是 .
7.(2021秋 嵩县期末)如图,AE∥CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD⊥BC,下列结论:①BC平分∠ABG;②AC∥BG;③与∠DBE互余的角有2个;④若∠A=α,则∠BDF=180°.其中正确的是 .(请把正确结论的序号都填上)
三.解答题
8.(2021春 凤山县期末)如图,已知∠1=∠2,∠C=∠F.请指出∠A与∠D的数量关系,并说明理由.
9.(2021春 陇县期末)如图,∠AEM+∠CDN=180°,EC平分∠AEF.若∠EFC=62°,求∠C的度数.
10.(2021春 江都区校级期中)已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2.
(1)那么DE与BC平行吗?为什么?
(2)如果∠B=40°,且∠A比∠ACB小10°,求∠DEC的度数.
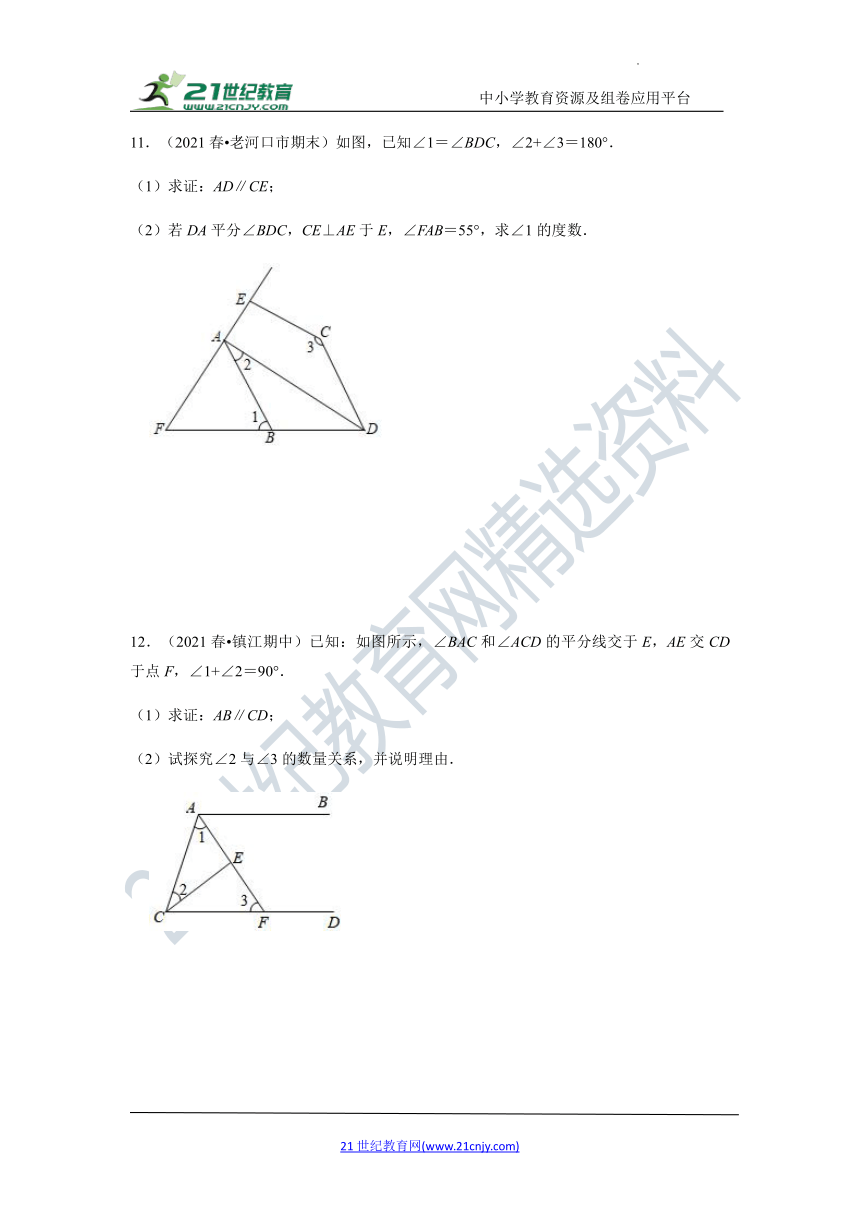
11.(2021春 老河口市期末)如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)求证:AD∥CE;
(2)若DA平分∠BDC,CE⊥AE于E,∠FAB=55°,求∠1的度数.
12.(2021春 镇江期中)已知:如图所示,∠BAC和∠ACD的平分线交于E,AE交CD于点F,∠1+∠2=90°.
(1)求证:AB∥CD;
(2)试探究∠2与∠3的数量关系,并说明理由.
13.(2021秋 禅城区期末)已知:如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点,∠AEG=∠AGE,∠C=∠DGC.
(1)求证:AB∥CD;
(2)若∠AGE+∠AHF=180°,求证:∠B=∠C;
(3)在(2)的条件下,若∠BFC=4∠C,求∠D的度数.
14.(2021秋 南岗区期末)已知:在四边形ABCD中,∠B=∠D,点E在边BC的延长线上,连接AE交CD于点F,若∠BAF+∠AFC=180°.
(1)如图1,求证:AD∥BC;
(2)如图2,过点D作DG∥AE交BE的延长线于点C,若∠G=∠B,在不添加任何辅助线的情况下,请直接写出图2中除∠B以外的四个与∠G相等的角.
15.(2021秋 安居区期末)如图,∠ADE+∠BCF=180°,AF平分∠BAD,∠BAD=2∠F.
(1)AD与BC平行吗?请说明理由.
(2)AB与EF的位置关系如何?为什么?
(3)若BE平分∠ABC.试说明:①∠ABC=2∠E;②∠E+∠F=90°.
16.(2021春 铁西区期末)如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)请直接写出直线AC与DG的位置关系;
(2)求证:BE∥CF;
(3)若∠C=35°,求∠BED的度数.
17.(2021春 广陵区校级期中)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠AEF与∠EFC的角平分线交于点P,EP延长线与CD交于点G,点H是MN上一点,且PF∥GH,试判断直GH与EG的位置关系,并说明理由.
18.(2021秋 嵩县期末)图1展示了光线反射定律:EF是镜面AB的垂线,一束光线m射到平面镜AB上,被AB反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角θ1=θ2.
(1)在图1中,证明:∠1=∠2.
(2)图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知∠1=30°,∠4=60°,判断直线m与直线n的位置关系,并说明理由.
(3)图3是潜望镜工作原理示意图,AB,CD是平行放置的两面平面镜.请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的?
19.(2021秋 上蔡县期末)已知:如图,AB∥CD∥GH,GH过点P.
(1)如图1,若∠BAP=40°,∠DCP=30°,则∠APC= (直接写出结果);
(2)如图2,直线MN分别交AB于点E,交CD于点F,点P在线段EF上,点Q在射线FC上.若∠MEB=110°,∠PQF=50°,求∠EPQ的度数;
(3)如图3,点P在射线FN上,点Q在射线FD上,∠AEF的平分线交CD于点O.若∠PQF∠MEB,试判断OE与PQ是否平行?并说明理由.
20.(2021春 汉阳区期中)如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,F,EM平分∠AEF交CD于点M,且∠FEM=∠FME.
(1)直线AB与直线CD的位置关系是 ;
(2)如图2,点G是射线FD上一动点(不与点F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.
①当点G在运动过程中,若β=56°,求α的度数;
②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.
21.(2021秋 南岗区校级期中)已知,直线EF分别与直线AB、CD相交于点G、H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD.
(2)如图2,点M在直线AB、CD之间,连接MG、HM,当∠AGM=32°,∠MHC=68°时,求∠GMH的度数.
(3)只保持(2)中所求∠GMH的度数不变,如图3,GP是∠AGM的平分线,HQ是∠MHD的平分线,作HN∥PG,则∠QHN的度数是否改变?若不发生改变,请求出它的度数.若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角)
22.(2021秋 香坊区校级期中)点E在射线DA上,点F、G为射线BC上两个动点,满足∠DBF=∠DEF,∠BDG=∠BGD,DG平分∠BDE.
(1)如图1,当点G在F右侧时,求证:BD∥EF;
(2)如图2,当点G在BF左侧时,求证:∠DGE=∠BDG+∠FEG;
(3)如图3,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分∠PDM,交EF于点N,连接NG,若DG⊥NG,∠B﹣∠DNG=∠EDN,求∠B的度数.
参考答案
1.【思路点拨】
根据对顶角相等得到∠2=∠5,结合∠1=∠2,得到∠1=∠5,即可判定l1∥l2,根据平行线的性质得出∠6=56°,再根据邻补角的定义求解即可.
【解题过程】
解:如图,
∵∠1=∠2,∠2=∠5,
∴∠1=∠5,
∴l1∥l2,
∴∠3=∠6,
∵∠3=56°,
∴∠6=56°,
∵∠4+∠6=180°,
∴∠4=180°﹣56°=124°,
故选:C.
2.【思路点拨】
由平行线的判定定理可得AC∥DE,由平行线的性质可得∠ACB=∠3,由平分线的定义可得∠ACB=2∠1=72°,即得∠3的度数.
【解题过程】
解:∵∠1=∠2=36°,
∴AC∥DE,
∴∠ACB=∠3,
∵CD平分∠ACB,
∴∠ACB=2∠1=72°,
∴∠3=72°.
故选:C.
3.【思路点拨】
①证明AB∥CD,可做判断;
②根据平行线的判定和性质可做判断;
③根据AF∥ED得内错角相等和同位角相等,再由角平分线的定义得∠ADE=∠CDE,从而可做判断.
【解题过程】
解:①∵AB⊥BC,DC⊥BC,
∴AB∥CD,
∴∠BAD+∠ADC=180°,
故①正确;
②∵AB∥CD,
∴∠AFD+∠BAF=180°,
∵∠BAF=∠EDF,
∴∠AFD+∠EDF=180°,
∴AF∥DE,
故②正确;
③∵AF∥ED,
∴∠DAF=∠ADE,∠F=∠CDE,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DAF=∠F,
故③正确;
故选:A.
4.【思路点拨】
由已知可得∠1+∠2=90°,∠3+∠2=90°,等量代换即可得出①结论;
延长EC,如图1,由已知条件可得∠1+∠5=90°,∠1+∠2=90°,可得∠2=∠5,根据平角的性质可得∠ACE+∠5=180°,等量代换即可得出②结论;
由已知条件可得∠A=∠2,∠ACE+∠2=180°,等量代换可得∠A+∠ACE=180°,根据平行线的判定即可得出③结论;
由平行线的性质可得∠E=∠4,由已知条件∠2=∠E,∠2=∠A,等量代换可得∠4=∠A.即可得出④结论.
【解题过程】
证明:∵AC⊥BC,DC⊥EC,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3.
故结论①正确;
延长EC,如图1,
∵DC⊥CE,AC⊥BC,
∴∠1+∠5=90°,∠1+∠2=90°,
∴∠2=∠5,
∵∠ACE+∠5=180°,
∴∠ACE+∠2=180°.
故结论②正确;
∵∠A=∠2,∠ACE+∠2=180°,
∴∠A+∠ACE=180°,
∴AB∥CE.
故结论③正确;
∵AB∥CE,
∴∠E=∠4,
∵∠2=∠E,∠2=∠A,
∴∠4=∠A.
故结论④正确.
所以结论正确的有①②③④.
故选:D.
5.【思路点拨】
①根据平行线的性质与判定即可判断;②∠AOC=∠EAP+∠E,而∠EAP∠EAD,∠E=∠ECD,即可判断;③利用平行线的性质和角平分线定义即可判断.
【解题过程】
解:∵AD∥BC,
∴∠BAD+∠B=180o,
∵∠B=∠D,
∴∠BAD+∠D=180o,
∴AB∥CD,故①正确;
∵AB∥CD,
∴∠ECD=∠E,
∵AP平分∠EAD,
∴∠EAP∠EAD
∵∠AOC=∠EAP+∠E,
∴∠AOC∠EAD+∠ECD,故②正确;
∴∠ECD=∠E=60o,
∵CP平分∠ECD,
∴∠ECP∠ECD=30°,
∵∠APC=70°,∠AOE=∠COP,
∴∠EAP=40°,
∵AP平分∠EAD,
∴∠EAD=2∠EAP=80°,
∵AB∥CD,
∴∠D=∠EAD=80°,故③正确;
故选:D.
6.【思路点拨】
由∠2与∠3间关系,可得到AB与CD的位置关系,利用角平分线的性质和平行线的性质可求得∠5度数.
【解题过程】
解:∵CB平分∠ACD,
∴∠1=∠2∠ACD..
∵∠2=∠3,
∴AB∥CD.
∴∠5=∠2,∠4=∠ACD=60°.
∴∠5=∠2=30°.
故答案为:30°.
7.【思路点拨】
根据平行线的性质得出∠A和∠ACB的关系,再根据角平分线的性质找出图中相等的角,由等角的余角相等即可得出结论.
【解题过程】
解:∵CBD=90°,
∴∠ABC+∠EBD=90°,
又∵∠DBG=∠EBD,
∴∠ABC=∠CBG,
∴BC平分∠ABG,
∴①正确,
∵∠GBC=∠ABC=∠ACB,
∴AC∥BG,
∴②正确,
∵∠DBE=∠DBG,
∴与∠DBE互余的角有∠ABC,∠GBC,∠ACB,∠GCB,有4个,
∴③错误,
∵∠BDF=180°﹣∠BDG,∠BDG=90°﹣∠CBG=90°﹣∠ACB,
又∵∠ACB(180°﹣α)=90°,
∴∠BDF=180°﹣[90°﹣(90°)]=180°,
∴④错误,
故答案为:①②.
8.【思路点拨】
根据∠1=∠2,∠3=∠2,可得∠1=∠3,得BF∥CE,根据平行线的性质得∠ABF=∠C,由∠C=∠F,得∠ABF=∠F,即可得出AC∥DF,得∠A和∠D的数量关系是相等.
【解题过程】
解:∠A和∠D的数量关系是相等.
理由是:如图,
∵∠1=∠2,∠3=∠2,
∴∠1=∠3,
∴BF∥CE,
∴∠ABF=∠C,
∵∠C=∠F,
∴∠ABF=∠F,
∴AC∥DF,
∴∠A=∠D.
9.【思路点拨】
根据同角的补角相等可得出∠AEM=∠CDM,利用“同位角相等,两直线平行”可得出AB∥CD,由“两直线平行,同旁内角互补”及∠EFC=62°可求出∠AEF=118°,结合角平分线的定义可求出∠AEC的度数,再利用“两直线平行,内错角相等”即可求出∠C的度数.
【解题过程】
解:∵∠CDM+∠CDN=180°,
又∵∠AEM+∠CDN=180°,
∴∠AEM=∠CDM,
∴AB∥CD,
∴∠AEF+∠EFC=180°,
∵∠EFC=62°,
∴∠AEF=118°,
∵EC平分∠AEF,
∴∠AEC=59°,
∵AB∥CD,
∴∠C=∠AEC=59°.
10.【思路点拨】
(1)根据CD⊥AB,FG⊥AB,可判定CD∥FG,利用平行线的性质可知∠2=∠BCD,已知∠1=∠2,等量代换得∠1=∠BCD,故可证DE与BC平行;
(2)根据三角形内角和求出∠ACB=75°,再根据平行线的性质即可求解.
【解题过程】
解:(1)DE∥BC,理由如下:
∵CD⊥AB,FG⊥AB,
∴CD∥FG.
∴∠2=∠BCD,
又∵∠1=∠2,
∴∠1=∠BCD,
∴DE∥BC;
(2)∵∠B=40°,∠ACB﹣10°=∠A,
∴∠ACB+(∠ACB﹣10°)+40°=180°,
∴∠ACB=75°,
由(1)知,DE∥BC,
∴∠DEC+∠ACB=180°,
∴∠DEC=105°.
11.【思路点拨】
(1)根据同位角相等,两直线平行可判定AB∥CD,得到∠2=∠ADC,等量代换得出∠ADC+∠3=180°,即可根据同旁内角互补,两直线平行得解;
(2)由CE⊥AE,AD∥CE得出∠DAF=∠CEF=90°,再根据平行线的性质即可求出∠ADC=∠2=35°,再根据角平分线的定义即可得解.
【解题过程】
(1)证明:∵∠1=∠BDC,
∴AB∥CD,
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴∠ADC+∠3=180°,
∴AD∥CE;
(2)解:∵CE⊥AE于E,
∴∠CEF=90°,
由(1)知AD∥CE,
∴∠DAF=∠CEF=90°,
∴∠ADC=∠2=∠DAF﹣∠FAB,
∵∠FAB=55°,
∴∠ADC=35°,
∵DA平分∠BDC,∠1=∠BDC,
∴∠1=∠BDC=2∠ADC=70°.
12.【思路点拨】
(1)根据角平分线定义得出∠BAC=2∠1,∠ACD=2∠2,根据∠1+∠2=90°得出∠BAC+∠ACD=180°,根据平行线的判定得出即可;
(2)根据平行线的性质和角平分线定义得出∠1=∠3,即可求出答案.
【解题过程】
(1)证明:∵∠BAC和∠ACD的平分线交于E,
∴∠BAC=2∠1,∠ACD=2∠2,
∵∠1+∠2=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)解:∠2+∠3=90°,理由如下:
∵AF平分∠BAC,
∴∠BAF=∠1,
∵AB∥CD,
∴∠BAF=∠3,
∴∠1=∠3,
∵∠1+∠2=90°,
∴∠2+∠3=90°.
13.【思路点拨】
(1)由对顶角相等可得∠AGE=∠DGC,从而可得∠AEG=∠C,则可判定AB∥CD;
(2)由平角的定义可得∠AGE+∠EGH=180°,从而可求得∠EGH=∠AHF,则可判定EC∥BF,则有∠B=∠AEG,从而可求证;
(3)由(2)得BF∥EC,则有∠C+∠BFC=180°,从而可求∠C的度数,利用三角形的内角和即可求∠D的度数.
【解题过程】
(1)证明:∵∠AEG=∠AGE,∠C=∠DGC,∠AGE=∠DGC,
∴∠AEG=∠C,
∴AB∥CD;
(2)证明:∵∠AGE+∠EGH=180°,∠AGE+∠AHF=180°,
∴∠EGH=∠AHF,
∴EC∥BF,
∴∠B=∠AEG,
∵AB∥CD,
∴∠C=∠AEG,
∴∠B=∠C;
(3)解:∵BF∥EC,
∴∠C+∠BFC=180°,
∵∠BFC=4∠C,
∴∠C+4∠C=180°,
解得∠C=36°,
∵∠C=∠DGC,
∴∠DGC=36°,
∴∠D=180°﹣∠C﹣∠DGC=108°.
14.【思路点拨】
(1)由已知条件可得AB∥CD,从而有∠B=∠ECD,则可求得∠D=∠ECD,即可得AD∥BC;
(2)利用平行线的性质进行求解即可.
【解题过程】
(1)证明:∵∠BAF+∠AFC=180°,
∴AB∥CD,
∴∠B=∠ECD,
∵∠B=∠D,
∴∠D=∠ECD,
∴AD∥BC;
(2)∵DG∥AE,
∴∠G=∠AEB,
由(1)得AD∥BC,
∴∠AEB=∠DAE,∠ADC=∠DCG,
∴∠G=∠DAE,
∵∠B=∠ADC,∠G=∠B,
∴∠G=∠ADC=∠DCG,
综上所述,所∠G相等的角有:∠AEB,∠DAE,∠ADC,∠DCG.
15.【思路点拨】
(1)由∠ADE+∠BCF=180°结合邻补角互补,可得出∠BCF=∠ADC,再利用“同位角相等,两直线平行”可得出AD∥BC;
(2)根据角平分线的定义及∠BAD=2∠F,可得出∠BAF=∠F,再利用“内错角相等,两直线平行”可得出AB∥EF;
(3)①由AB∥EF,利用“两直线平行,内错角相等”可得出∠ABE=∠E,结合角平分线的定义可得出∠ABC=2∠E;
②由AD∥BC,利用“两直线平行,同旁内角互补”可得出∠BAD+∠ABC=180°,再结合∠BAD=2∠F,∠ABC=2∠E可得出∠E+∠F=90°.
【解题过程】
解:(1)AD∥BC,理由如下:
∵∠ADE+∠BCF=180°,∠ADE+∠ADC=180°,
∴∠BCF=∠ADC,
∴AD∥BC.
(2)AB∥EF,理由如下:
∵AF平分∠BAD,∠BAD=2∠F,
∴∠BAF∠BAD=∠F,
∴AB∥EF.
(3)①∠ABC=2∠E,理由如下:
∵AB∥EF,
∴∠ABE=∠E.
∵BE平分∠ABC,
∴∠ABC=2∠ABE=2∠E.
②∠E+∠F=90°,理由如下:
∵AD∥BC,
∴∠BAD+∠ABC=180°.
∵∠BAD=2∠F,∠ABC=2∠E,
∴2∠E+2∠F=180°,
∴∠E+∠F=90°.
16.【思路点拨】
(1)由对顶角相等可得∠ABF=∠1,从而有∠ABF=∠2,即可得AC∥DG;
(2)求出∠1=∠BFG,根据平行线的判定得出AC∥DG,求出∠EBF=∠BFC,根据平行线的判定得出即可;
(3)根据平行线的性质得出∠C=∠CFG=∠BEF=35°,再求出答案即可.
【解题过程】
解:(1)AC∥DG,理由如下:
∵∠ABF=∠1,∠1=∠2,
∴∠ABF=∠2,
∴AC∥DG;
(2)由(1)知AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴,∠CFB∠BFG,
∴∠EBF=∠CFB,
∴BE∥CF.
(3)∵AC∥DG,∠C=35°,
∴∠C=∠CFG=35°,
∵BE∥CF,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
17.【思路点拨】
(1)利用邻补角的定义及已知得出∠1=∠CFE,即可判定AB∥CD;
(2)利用(1)中平行线的性质推知∠AEF+∠EFC=180°,然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG⊥PF,故结合已知条件PF∥GH,易证GH⊥EG;
【解题过程】
解:(1)AB∥CD,理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
又∵∠2+∠CFE=180°,
∴∠1=∠CFE,
∴AB∥CD;
(2)GH⊥EG,理由如下:
由(1)知,AB∥CD,
∴∠AEF+∠EFC=180°.
又∵∠AEF与∠EFC的角平分线交于点P,
∴∠FEP+∠EFP(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF,
∵PF∥GH,
∴GH⊥EG.
18.【思路点拨】
(1)根据角的关系解答即可;
(2)求出∠5+∠6=180°,根据平行线的判定得出即可;
(3)根据平行线的性质和平均的定义得到∠5=∠6,根据平行线的判定得出即可.
【解题过程】
(1)证明:∵∠AFE=∠BFE=90°,
∵θ1=θ2.
∴∠1=∠2;
(2)解:直线m∥直线n,
理由:如图2,
∵∠1=∠2=30°,∠3=∠4=60°,
∴∠5=180°﹣∠1﹣∠2=120°,∠6=180°﹣∠3﹣∠4=60°,
∴∠5+∠6=180°,
∴直线m∥直线n;
(3)解:∵AB∥CD,
∴∠2=∠3,
∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4,
∴180°﹣∠1﹣∠2=180°﹣∠3﹣∠4,
即:∠5=∠6,
∴m∥n.
19.【思路点拨】
(1)依据平行线的性质,即可得到∠APG=∠BAP=40°,∠CPG=∠DCP=30,再根据∠APC=∠APG+∠CPG进行计算即可;
(2)利用邻补角的定义可得∠BEP=180°﹣110°=70°,利用(1)的结论即可得∠EPQ的度数;
(3)根据对顶角相等以及角平分线的定义可得∠PQF∠MEB∠AEF=∠AEO,再根据平行线的性质∠AEO=∠EOF,可得∠PQF=∠EOF,根据内错角相等两直线平行即可得OE∥PQ.
【解题过程】
解:(1)∵AB∥CD∥GH,
∴∠APG=∠BAP=40°,∠CPG=∠DCP=30,
∴∠APC=∠APG+∠CPG=40°+30°=70°,
故答案为:70°;
(2)∵∠MEB=110°,
∴∠BEP=180°﹣110°=70°,
由(1)可得:∠EPQ=∠EPG+∠QPG=∠BEP+∠PQF=70°+50°=120°;
(3)OE∥PQ.
理由:∵∠PQF∠MEB,∠MEB=∠AEF,
∴∠PQF∠MEB∠AEF,
∵EO平分∠AEF.
∴∠PQF∠AEF=∠AEO,
∵AB∥CD,
∴∠AEO=∠EOF,
∴∠PQF=∠EOF,
∴OE∥PQ.
20.【思路点拨】
(1)根据角平分线的性质可得∠AEM=∠FEM,由已知条件∠FEM=∠FME,等量代换可得∠AEM=∠FME,由平行线的判定即可得出答案;
(2)由平行线的性质可得β=∠GEB,由平角的性质可得∠AED=180°﹣∠GEB,根据角平分线的性质可得∠CEF,∠FEH,由∠CEH=∠CEF+∠FEH可计算出度数,根据垂线的性质可得α+∠CEH=90°,代入计算即可得出答案;
(3)证明方法同(2).
【解题过程】
证明:(1)∵EM平分∠AEF,
∴∠AEM=∠FEM,
∵∠FEM=∠FME,
∴∠AEM=∠FME,
∴AB∥CD.
故答案为:AB∥CD;
(2)①∵AB∥CD,
∴β=∠GEB=56°,
∴∠AEG=180°﹣∠GEB=180°﹣56°=124°,
∵EH平分∠FEG,EM平分∠AEF,
∴∠CEF,∠FEH,
∴∠CEH=∠CEF+∠FEH,
∵HN⊥EM,
∴α+∠CEH=90°,
∴α=90°﹣∠CEH=90°﹣62°=28°;
②a.理由如下:
∵AB∥CD,
∴β=∠GEB,
∴∠AED=180°﹣∠GEB=180°﹣β,
∵EH平分∠FEG,EM平分∠AEF,
∴∠CEF,∠FEH,
∴∠CEH=∠CEF+∠FEH,
∵HN⊥EM,
∴α+∠CEH=90°,
∴α90°,
即a.
21.【思路点拨】
(1)先由邻补角得到∠AGE+∠BGE=180°,然后结合∠AGE+∠DHE=180°得到∠BGE=∠DHE,最后得证AB∥CD;
(2)先由AB∥CD得到∠AGH+∠CHG=180°,即∠AGM+∠MGH+∠MHG+∠MHC=180°,再结合∠MGH+∠MHG+∠GMH=180°得到∠GMH=∠AGM+∠MHC,最后结合已知条件得到∠GMH的大小;
(3)先由(2)得到∠AGM+∠MHC=∠GMH=100°,∠MGH+∠MHG=80°,然后结合角平分线的定义得到∠MGP和∠MHQ,再结合HN∥PG得到∠GHN=∠PGH,最后由∠QHN=∠GHN﹣∠GHQ求得∠QHN的大小.
【解题过程】
(1)证明:∵∠AGE+∠BGE=180°,∠AGE+∠DHE=180°,
∴∠BGE=∠DHE,
∴AB∥CD.
(2)解:∵AB∥CD,
∴∠AGH+∠CHG=180°,即∠AGM+∠MGH+∠MHG+∠MHC=180°,
∵∠MGH+∠MHG+∠GMH=180°,
∴∠GMH=∠AGM+∠MHC,
∵∠AGM=32°,∠MHC=68°,
∴∠GMH=100°.
(3)解:∠QHN的度数不发生改变,理由如下,
由(2)得,∠AGM+∠MHC=∠GMH=100°,
∴∠MGH+∠MHG=80°,
∵GP、HQ分别平分∠MGA和∠MHD,
∴∠MGP∠MGA,∠MHQ∠MHD(180°﹣∠MHC)=90°∠MHC,
∴∠PGH=∠MGP+∠MGH∠MGA+∠MGH,
∵HN∥PG,
∴∠GHN=∠PGH∠MGA+∠MGH,
∴∠QHN=∠GHN﹣∠GHQ=(∠MGA+∠MGH)﹣(∠MHQ﹣∠MHG)∠MGA+∠MGH﹣∠MHQ+∠MHG∠MGA+80°﹣∠MHQ,
∴∠QHN∠MGA+80°﹣(90°∠MHC)=﹣10°(∠MGA+∠MHC)=﹣10°100°=40°.
22.【思路点拨】
(1)通过证明∠DBF=∠EFG,利用同位角相等,两直线平行即可得出结论;
(2)过点E作GH∥BD,交AD于点H,利用(1)的结论和平行线的性质即可得出结论;
(3)设∠BDM=∠MDG=α,则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α,∠PDM=180°﹣α;利用已知条件用含α的式子表示∠PDN,∠EDN,∠GDN,∠DNG,再利用∠B﹣∠DNG=∠EDN,得到关于α的方程,解方程求得α的值,则∠B=180°﹣4α,结论可求.
【解题过程】
证明:(1)∵DG平分∠BDE,
∴∠BDG=∠ADG.
又∵∠BDG=∠BGD,
∴∠ADG=∠DGB.
∴AD∥BC.
∴∠DEF=∠EFG.
∵∠DBF=∠DEF,
∴∠DBF=∠EFG.
∴BD∥EF.
(2)过点G作GH∥BD,交AD于点H,如图,
∵BD∥EF,
∴GH∥EF.
∴∠BDG=∠DGH,∠GEF=∠HGE,
∵∠DGE=∠DGH+∠HGE,
∴∠DGE=∠BDG+∠FEG.
(3)设∠BDM=∠MDG=α,
则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α.
∴∠PDM=180°﹣α.
∵DN平分∠PDM
∴.
∴.
∴∠GDN=∠MDN﹣∠MDG=90°α=90°.
∵DG⊥ON,
∴∠DNG=90°.
∴.
∵DE∥BF,
∴∠B=∠PDE=180°﹣4α.
∵∠B﹣∠DNG=∠EDN,
∴,
解得:α=30°.
∴∠B=180°﹣4α=60°
21世纪教育网(www.21cnjy.com)
人教版七年级数学下册专练
平行线的判定与性质
一.选择题
1.(2021 鞍山一模)如图,∠1=∠2=∠3=56°,则∠4的度数是( )
A.56° B.114° C.124° D.146°
2.(2021 雁塔区校级模拟)如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=( )
A.36° B.52° C.72° D.80°
3.(2021春 单县期末)如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个
C.1个 D.0个
4.(2021春 德宏州期末)如图所示,AC⊥BC,DC⊥EC,则下列结论:①∠1=∠3;②∠ACE+∠2=180°;③若∠A=∠2,则有AB∥CE;④若∠2=∠E,则有∠4=∠A.其中正确的有( )
A.①②③ B.①②④
C.③④ D.①②③④
5.(2021春 汉川市期末)如图,AD∥BC,∠B=∠D,延长BA至点E,连接CE,∠EAD和∠ECD的角平分线交于点P.下列三个结论:①AB∥CD;②∠AOC∠EAD+∠ECD;③若∠E=60°,∠APC=70°,则∠D=80°.其中结论正确的个数有( )
A.0 B.1
C.2 D.3
二.填空题
6.(2021春 夏津县期末)如图,CB平分∠ACD,∠2=∠3,若∠4=60°,则∠5的度数是 .
7.(2021秋 嵩县期末)如图,AE∥CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD⊥BC,下列结论:①BC平分∠ABG;②AC∥BG;③与∠DBE互余的角有2个;④若∠A=α,则∠BDF=180°.其中正确的是 .(请把正确结论的序号都填上)
三.解答题
8.(2021春 凤山县期末)如图,已知∠1=∠2,∠C=∠F.请指出∠A与∠D的数量关系,并说明理由.
9.(2021春 陇县期末)如图,∠AEM+∠CDN=180°,EC平分∠AEF.若∠EFC=62°,求∠C的度数.
10.(2021春 江都区校级期中)已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2.
(1)那么DE与BC平行吗?为什么?
(2)如果∠B=40°,且∠A比∠ACB小10°,求∠DEC的度数.
11.(2021春 老河口市期末)如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)求证:AD∥CE;
(2)若DA平分∠BDC,CE⊥AE于E,∠FAB=55°,求∠1的度数.
12.(2021春 镇江期中)已知:如图所示,∠BAC和∠ACD的平分线交于E,AE交CD于点F,∠1+∠2=90°.
(1)求证:AB∥CD;
(2)试探究∠2与∠3的数量关系,并说明理由.
13.(2021秋 禅城区期末)已知:如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点,∠AEG=∠AGE,∠C=∠DGC.
(1)求证:AB∥CD;
(2)若∠AGE+∠AHF=180°,求证:∠B=∠C;
(3)在(2)的条件下,若∠BFC=4∠C,求∠D的度数.
14.(2021秋 南岗区期末)已知:在四边形ABCD中,∠B=∠D,点E在边BC的延长线上,连接AE交CD于点F,若∠BAF+∠AFC=180°.
(1)如图1,求证:AD∥BC;
(2)如图2,过点D作DG∥AE交BE的延长线于点C,若∠G=∠B,在不添加任何辅助线的情况下,请直接写出图2中除∠B以外的四个与∠G相等的角.
15.(2021秋 安居区期末)如图,∠ADE+∠BCF=180°,AF平分∠BAD,∠BAD=2∠F.
(1)AD与BC平行吗?请说明理由.
(2)AB与EF的位置关系如何?为什么?
(3)若BE平分∠ABC.试说明:①∠ABC=2∠E;②∠E+∠F=90°.
16.(2021春 铁西区期末)如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)请直接写出直线AC与DG的位置关系;
(2)求证:BE∥CF;
(3)若∠C=35°,求∠BED的度数.
17.(2021春 广陵区校级期中)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠AEF与∠EFC的角平分线交于点P,EP延长线与CD交于点G,点H是MN上一点,且PF∥GH,试判断直GH与EG的位置关系,并说明理由.
18.(2021秋 嵩县期末)图1展示了光线反射定律:EF是镜面AB的垂线,一束光线m射到平面镜AB上,被AB反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角θ1=θ2.
(1)在图1中,证明:∠1=∠2.
(2)图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知∠1=30°,∠4=60°,判断直线m与直线n的位置关系,并说明理由.
(3)图3是潜望镜工作原理示意图,AB,CD是平行放置的两面平面镜.请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的?
19.(2021秋 上蔡县期末)已知:如图,AB∥CD∥GH,GH过点P.
(1)如图1,若∠BAP=40°,∠DCP=30°,则∠APC= (直接写出结果);
(2)如图2,直线MN分别交AB于点E,交CD于点F,点P在线段EF上,点Q在射线FC上.若∠MEB=110°,∠PQF=50°,求∠EPQ的度数;
(3)如图3,点P在射线FN上,点Q在射线FD上,∠AEF的平分线交CD于点O.若∠PQF∠MEB,试判断OE与PQ是否平行?并说明理由.
20.(2021春 汉阳区期中)如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,F,EM平分∠AEF交CD于点M,且∠FEM=∠FME.
(1)直线AB与直线CD的位置关系是 ;
(2)如图2,点G是射线FD上一动点(不与点F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.
①当点G在运动过程中,若β=56°,求α的度数;
②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.
21.(2021秋 南岗区校级期中)已知,直线EF分别与直线AB、CD相交于点G、H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD.
(2)如图2,点M在直线AB、CD之间,连接MG、HM,当∠AGM=32°,∠MHC=68°时,求∠GMH的度数.
(3)只保持(2)中所求∠GMH的度数不变,如图3,GP是∠AGM的平分线,HQ是∠MHD的平分线,作HN∥PG,则∠QHN的度数是否改变?若不发生改变,请求出它的度数.若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角)
22.(2021秋 香坊区校级期中)点E在射线DA上,点F、G为射线BC上两个动点,满足∠DBF=∠DEF,∠BDG=∠BGD,DG平分∠BDE.
(1)如图1,当点G在F右侧时,求证:BD∥EF;
(2)如图2,当点G在BF左侧时,求证:∠DGE=∠BDG+∠FEG;
(3)如图3,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分∠PDM,交EF于点N,连接NG,若DG⊥NG,∠B﹣∠DNG=∠EDN,求∠B的度数.
参考答案
1.【思路点拨】
根据对顶角相等得到∠2=∠5,结合∠1=∠2,得到∠1=∠5,即可判定l1∥l2,根据平行线的性质得出∠6=56°,再根据邻补角的定义求解即可.
【解题过程】
解:如图,
∵∠1=∠2,∠2=∠5,
∴∠1=∠5,
∴l1∥l2,
∴∠3=∠6,
∵∠3=56°,
∴∠6=56°,
∵∠4+∠6=180°,
∴∠4=180°﹣56°=124°,
故选:C.
2.【思路点拨】
由平行线的判定定理可得AC∥DE,由平行线的性质可得∠ACB=∠3,由平分线的定义可得∠ACB=2∠1=72°,即得∠3的度数.
【解题过程】
解:∵∠1=∠2=36°,
∴AC∥DE,
∴∠ACB=∠3,
∵CD平分∠ACB,
∴∠ACB=2∠1=72°,
∴∠3=72°.
故选:C.
3.【思路点拨】
①证明AB∥CD,可做判断;
②根据平行线的判定和性质可做判断;
③根据AF∥ED得内错角相等和同位角相等,再由角平分线的定义得∠ADE=∠CDE,从而可做判断.
【解题过程】
解:①∵AB⊥BC,DC⊥BC,
∴AB∥CD,
∴∠BAD+∠ADC=180°,
故①正确;
②∵AB∥CD,
∴∠AFD+∠BAF=180°,
∵∠BAF=∠EDF,
∴∠AFD+∠EDF=180°,
∴AF∥DE,
故②正确;
③∵AF∥ED,
∴∠DAF=∠ADE,∠F=∠CDE,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DAF=∠F,
故③正确;
故选:A.
4.【思路点拨】
由已知可得∠1+∠2=90°,∠3+∠2=90°,等量代换即可得出①结论;
延长EC,如图1,由已知条件可得∠1+∠5=90°,∠1+∠2=90°,可得∠2=∠5,根据平角的性质可得∠ACE+∠5=180°,等量代换即可得出②结论;
由已知条件可得∠A=∠2,∠ACE+∠2=180°,等量代换可得∠A+∠ACE=180°,根据平行线的判定即可得出③结论;
由平行线的性质可得∠E=∠4,由已知条件∠2=∠E,∠2=∠A,等量代换可得∠4=∠A.即可得出④结论.
【解题过程】
证明:∵AC⊥BC,DC⊥EC,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3.
故结论①正确;
延长EC,如图1,
∵DC⊥CE,AC⊥BC,
∴∠1+∠5=90°,∠1+∠2=90°,
∴∠2=∠5,
∵∠ACE+∠5=180°,
∴∠ACE+∠2=180°.
故结论②正确;
∵∠A=∠2,∠ACE+∠2=180°,
∴∠A+∠ACE=180°,
∴AB∥CE.
故结论③正确;
∵AB∥CE,
∴∠E=∠4,
∵∠2=∠E,∠2=∠A,
∴∠4=∠A.
故结论④正确.
所以结论正确的有①②③④.
故选:D.
5.【思路点拨】
①根据平行线的性质与判定即可判断;②∠AOC=∠EAP+∠E,而∠EAP∠EAD,∠E=∠ECD,即可判断;③利用平行线的性质和角平分线定义即可判断.
【解题过程】
解:∵AD∥BC,
∴∠BAD+∠B=180o,
∵∠B=∠D,
∴∠BAD+∠D=180o,
∴AB∥CD,故①正确;
∵AB∥CD,
∴∠ECD=∠E,
∵AP平分∠EAD,
∴∠EAP∠EAD
∵∠AOC=∠EAP+∠E,
∴∠AOC∠EAD+∠ECD,故②正确;
∴∠ECD=∠E=60o,
∵CP平分∠ECD,
∴∠ECP∠ECD=30°,
∵∠APC=70°,∠AOE=∠COP,
∴∠EAP=40°,
∵AP平分∠EAD,
∴∠EAD=2∠EAP=80°,
∵AB∥CD,
∴∠D=∠EAD=80°,故③正确;
故选:D.
6.【思路点拨】
由∠2与∠3间关系,可得到AB与CD的位置关系,利用角平分线的性质和平行线的性质可求得∠5度数.
【解题过程】
解:∵CB平分∠ACD,
∴∠1=∠2∠ACD..
∵∠2=∠3,
∴AB∥CD.
∴∠5=∠2,∠4=∠ACD=60°.
∴∠5=∠2=30°.
故答案为:30°.
7.【思路点拨】
根据平行线的性质得出∠A和∠ACB的关系,再根据角平分线的性质找出图中相等的角,由等角的余角相等即可得出结论.
【解题过程】
解:∵CBD=90°,
∴∠ABC+∠EBD=90°,
又∵∠DBG=∠EBD,
∴∠ABC=∠CBG,
∴BC平分∠ABG,
∴①正确,
∵∠GBC=∠ABC=∠ACB,
∴AC∥BG,
∴②正确,
∵∠DBE=∠DBG,
∴与∠DBE互余的角有∠ABC,∠GBC,∠ACB,∠GCB,有4个,
∴③错误,
∵∠BDF=180°﹣∠BDG,∠BDG=90°﹣∠CBG=90°﹣∠ACB,
又∵∠ACB(180°﹣α)=90°,
∴∠BDF=180°﹣[90°﹣(90°)]=180°,
∴④错误,
故答案为:①②.
8.【思路点拨】
根据∠1=∠2,∠3=∠2,可得∠1=∠3,得BF∥CE,根据平行线的性质得∠ABF=∠C,由∠C=∠F,得∠ABF=∠F,即可得出AC∥DF,得∠A和∠D的数量关系是相等.
【解题过程】
解:∠A和∠D的数量关系是相等.
理由是:如图,
∵∠1=∠2,∠3=∠2,
∴∠1=∠3,
∴BF∥CE,
∴∠ABF=∠C,
∵∠C=∠F,
∴∠ABF=∠F,
∴AC∥DF,
∴∠A=∠D.
9.【思路点拨】
根据同角的补角相等可得出∠AEM=∠CDM,利用“同位角相等,两直线平行”可得出AB∥CD,由“两直线平行,同旁内角互补”及∠EFC=62°可求出∠AEF=118°,结合角平分线的定义可求出∠AEC的度数,再利用“两直线平行,内错角相等”即可求出∠C的度数.
【解题过程】
解:∵∠CDM+∠CDN=180°,
又∵∠AEM+∠CDN=180°,
∴∠AEM=∠CDM,
∴AB∥CD,
∴∠AEF+∠EFC=180°,
∵∠EFC=62°,
∴∠AEF=118°,
∵EC平分∠AEF,
∴∠AEC=59°,
∵AB∥CD,
∴∠C=∠AEC=59°.
10.【思路点拨】
(1)根据CD⊥AB,FG⊥AB,可判定CD∥FG,利用平行线的性质可知∠2=∠BCD,已知∠1=∠2,等量代换得∠1=∠BCD,故可证DE与BC平行;
(2)根据三角形内角和求出∠ACB=75°,再根据平行线的性质即可求解.
【解题过程】
解:(1)DE∥BC,理由如下:
∵CD⊥AB,FG⊥AB,
∴CD∥FG.
∴∠2=∠BCD,
又∵∠1=∠2,
∴∠1=∠BCD,
∴DE∥BC;
(2)∵∠B=40°,∠ACB﹣10°=∠A,
∴∠ACB+(∠ACB﹣10°)+40°=180°,
∴∠ACB=75°,
由(1)知,DE∥BC,
∴∠DEC+∠ACB=180°,
∴∠DEC=105°.
11.【思路点拨】
(1)根据同位角相等,两直线平行可判定AB∥CD,得到∠2=∠ADC,等量代换得出∠ADC+∠3=180°,即可根据同旁内角互补,两直线平行得解;
(2)由CE⊥AE,AD∥CE得出∠DAF=∠CEF=90°,再根据平行线的性质即可求出∠ADC=∠2=35°,再根据角平分线的定义即可得解.
【解题过程】
(1)证明:∵∠1=∠BDC,
∴AB∥CD,
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴∠ADC+∠3=180°,
∴AD∥CE;
(2)解:∵CE⊥AE于E,
∴∠CEF=90°,
由(1)知AD∥CE,
∴∠DAF=∠CEF=90°,
∴∠ADC=∠2=∠DAF﹣∠FAB,
∵∠FAB=55°,
∴∠ADC=35°,
∵DA平分∠BDC,∠1=∠BDC,
∴∠1=∠BDC=2∠ADC=70°.
12.【思路点拨】
(1)根据角平分线定义得出∠BAC=2∠1,∠ACD=2∠2,根据∠1+∠2=90°得出∠BAC+∠ACD=180°,根据平行线的判定得出即可;
(2)根据平行线的性质和角平分线定义得出∠1=∠3,即可求出答案.
【解题过程】
(1)证明:∵∠BAC和∠ACD的平分线交于E,
∴∠BAC=2∠1,∠ACD=2∠2,
∵∠1+∠2=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)解:∠2+∠3=90°,理由如下:
∵AF平分∠BAC,
∴∠BAF=∠1,
∵AB∥CD,
∴∠BAF=∠3,
∴∠1=∠3,
∵∠1+∠2=90°,
∴∠2+∠3=90°.
13.【思路点拨】
(1)由对顶角相等可得∠AGE=∠DGC,从而可得∠AEG=∠C,则可判定AB∥CD;
(2)由平角的定义可得∠AGE+∠EGH=180°,从而可求得∠EGH=∠AHF,则可判定EC∥BF,则有∠B=∠AEG,从而可求证;
(3)由(2)得BF∥EC,则有∠C+∠BFC=180°,从而可求∠C的度数,利用三角形的内角和即可求∠D的度数.
【解题过程】
(1)证明:∵∠AEG=∠AGE,∠C=∠DGC,∠AGE=∠DGC,
∴∠AEG=∠C,
∴AB∥CD;
(2)证明:∵∠AGE+∠EGH=180°,∠AGE+∠AHF=180°,
∴∠EGH=∠AHF,
∴EC∥BF,
∴∠B=∠AEG,
∵AB∥CD,
∴∠C=∠AEG,
∴∠B=∠C;
(3)解:∵BF∥EC,
∴∠C+∠BFC=180°,
∵∠BFC=4∠C,
∴∠C+4∠C=180°,
解得∠C=36°,
∵∠C=∠DGC,
∴∠DGC=36°,
∴∠D=180°﹣∠C﹣∠DGC=108°.
14.【思路点拨】
(1)由已知条件可得AB∥CD,从而有∠B=∠ECD,则可求得∠D=∠ECD,即可得AD∥BC;
(2)利用平行线的性质进行求解即可.
【解题过程】
(1)证明:∵∠BAF+∠AFC=180°,
∴AB∥CD,
∴∠B=∠ECD,
∵∠B=∠D,
∴∠D=∠ECD,
∴AD∥BC;
(2)∵DG∥AE,
∴∠G=∠AEB,
由(1)得AD∥BC,
∴∠AEB=∠DAE,∠ADC=∠DCG,
∴∠G=∠DAE,
∵∠B=∠ADC,∠G=∠B,
∴∠G=∠ADC=∠DCG,
综上所述,所∠G相等的角有:∠AEB,∠DAE,∠ADC,∠DCG.
15.【思路点拨】
(1)由∠ADE+∠BCF=180°结合邻补角互补,可得出∠BCF=∠ADC,再利用“同位角相等,两直线平行”可得出AD∥BC;
(2)根据角平分线的定义及∠BAD=2∠F,可得出∠BAF=∠F,再利用“内错角相等,两直线平行”可得出AB∥EF;
(3)①由AB∥EF,利用“两直线平行,内错角相等”可得出∠ABE=∠E,结合角平分线的定义可得出∠ABC=2∠E;
②由AD∥BC,利用“两直线平行,同旁内角互补”可得出∠BAD+∠ABC=180°,再结合∠BAD=2∠F,∠ABC=2∠E可得出∠E+∠F=90°.
【解题过程】
解:(1)AD∥BC,理由如下:
∵∠ADE+∠BCF=180°,∠ADE+∠ADC=180°,
∴∠BCF=∠ADC,
∴AD∥BC.
(2)AB∥EF,理由如下:
∵AF平分∠BAD,∠BAD=2∠F,
∴∠BAF∠BAD=∠F,
∴AB∥EF.
(3)①∠ABC=2∠E,理由如下:
∵AB∥EF,
∴∠ABE=∠E.
∵BE平分∠ABC,
∴∠ABC=2∠ABE=2∠E.
②∠E+∠F=90°,理由如下:
∵AD∥BC,
∴∠BAD+∠ABC=180°.
∵∠BAD=2∠F,∠ABC=2∠E,
∴2∠E+2∠F=180°,
∴∠E+∠F=90°.
16.【思路点拨】
(1)由对顶角相等可得∠ABF=∠1,从而有∠ABF=∠2,即可得AC∥DG;
(2)求出∠1=∠BFG,根据平行线的判定得出AC∥DG,求出∠EBF=∠BFC,根据平行线的判定得出即可;
(3)根据平行线的性质得出∠C=∠CFG=∠BEF=35°,再求出答案即可.
【解题过程】
解:(1)AC∥DG,理由如下:
∵∠ABF=∠1,∠1=∠2,
∴∠ABF=∠2,
∴AC∥DG;
(2)由(1)知AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴,∠CFB∠BFG,
∴∠EBF=∠CFB,
∴BE∥CF.
(3)∵AC∥DG,∠C=35°,
∴∠C=∠CFG=35°,
∵BE∥CF,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
17.【思路点拨】
(1)利用邻补角的定义及已知得出∠1=∠CFE,即可判定AB∥CD;
(2)利用(1)中平行线的性质推知∠AEF+∠EFC=180°,然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG⊥PF,故结合已知条件PF∥GH,易证GH⊥EG;
【解题过程】
解:(1)AB∥CD,理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
又∵∠2+∠CFE=180°,
∴∠1=∠CFE,
∴AB∥CD;
(2)GH⊥EG,理由如下:
由(1)知,AB∥CD,
∴∠AEF+∠EFC=180°.
又∵∠AEF与∠EFC的角平分线交于点P,
∴∠FEP+∠EFP(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF,
∵PF∥GH,
∴GH⊥EG.
18.【思路点拨】
(1)根据角的关系解答即可;
(2)求出∠5+∠6=180°,根据平行线的判定得出即可;
(3)根据平行线的性质和平均的定义得到∠5=∠6,根据平行线的判定得出即可.
【解题过程】
(1)证明:∵∠AFE=∠BFE=90°,
∵θ1=θ2.
∴∠1=∠2;
(2)解:直线m∥直线n,
理由:如图2,
∵∠1=∠2=30°,∠3=∠4=60°,
∴∠5=180°﹣∠1﹣∠2=120°,∠6=180°﹣∠3﹣∠4=60°,
∴∠5+∠6=180°,
∴直线m∥直线n;
(3)解:∵AB∥CD,
∴∠2=∠3,
∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4,
∴180°﹣∠1﹣∠2=180°﹣∠3﹣∠4,
即:∠5=∠6,
∴m∥n.
19.【思路点拨】
(1)依据平行线的性质,即可得到∠APG=∠BAP=40°,∠CPG=∠DCP=30,再根据∠APC=∠APG+∠CPG进行计算即可;
(2)利用邻补角的定义可得∠BEP=180°﹣110°=70°,利用(1)的结论即可得∠EPQ的度数;
(3)根据对顶角相等以及角平分线的定义可得∠PQF∠MEB∠AEF=∠AEO,再根据平行线的性质∠AEO=∠EOF,可得∠PQF=∠EOF,根据内错角相等两直线平行即可得OE∥PQ.
【解题过程】
解:(1)∵AB∥CD∥GH,
∴∠APG=∠BAP=40°,∠CPG=∠DCP=30,
∴∠APC=∠APG+∠CPG=40°+30°=70°,
故答案为:70°;
(2)∵∠MEB=110°,
∴∠BEP=180°﹣110°=70°,
由(1)可得:∠EPQ=∠EPG+∠QPG=∠BEP+∠PQF=70°+50°=120°;
(3)OE∥PQ.
理由:∵∠PQF∠MEB,∠MEB=∠AEF,
∴∠PQF∠MEB∠AEF,
∵EO平分∠AEF.
∴∠PQF∠AEF=∠AEO,
∵AB∥CD,
∴∠AEO=∠EOF,
∴∠PQF=∠EOF,
∴OE∥PQ.
20.【思路点拨】
(1)根据角平分线的性质可得∠AEM=∠FEM,由已知条件∠FEM=∠FME,等量代换可得∠AEM=∠FME,由平行线的判定即可得出答案;
(2)由平行线的性质可得β=∠GEB,由平角的性质可得∠AED=180°﹣∠GEB,根据角平分线的性质可得∠CEF,∠FEH,由∠CEH=∠CEF+∠FEH可计算出度数,根据垂线的性质可得α+∠CEH=90°,代入计算即可得出答案;
(3)证明方法同(2).
【解题过程】
证明:(1)∵EM平分∠AEF,
∴∠AEM=∠FEM,
∵∠FEM=∠FME,
∴∠AEM=∠FME,
∴AB∥CD.
故答案为:AB∥CD;
(2)①∵AB∥CD,
∴β=∠GEB=56°,
∴∠AEG=180°﹣∠GEB=180°﹣56°=124°,
∵EH平分∠FEG,EM平分∠AEF,
∴∠CEF,∠FEH,
∴∠CEH=∠CEF+∠FEH,
∵HN⊥EM,
∴α+∠CEH=90°,
∴α=90°﹣∠CEH=90°﹣62°=28°;
②a.理由如下:
∵AB∥CD,
∴β=∠GEB,
∴∠AED=180°﹣∠GEB=180°﹣β,
∵EH平分∠FEG,EM平分∠AEF,
∴∠CEF,∠FEH,
∴∠CEH=∠CEF+∠FEH,
∵HN⊥EM,
∴α+∠CEH=90°,
∴α90°,
即a.
21.【思路点拨】
(1)先由邻补角得到∠AGE+∠BGE=180°,然后结合∠AGE+∠DHE=180°得到∠BGE=∠DHE,最后得证AB∥CD;
(2)先由AB∥CD得到∠AGH+∠CHG=180°,即∠AGM+∠MGH+∠MHG+∠MHC=180°,再结合∠MGH+∠MHG+∠GMH=180°得到∠GMH=∠AGM+∠MHC,最后结合已知条件得到∠GMH的大小;
(3)先由(2)得到∠AGM+∠MHC=∠GMH=100°,∠MGH+∠MHG=80°,然后结合角平分线的定义得到∠MGP和∠MHQ,再结合HN∥PG得到∠GHN=∠PGH,最后由∠QHN=∠GHN﹣∠GHQ求得∠QHN的大小.
【解题过程】
(1)证明:∵∠AGE+∠BGE=180°,∠AGE+∠DHE=180°,
∴∠BGE=∠DHE,
∴AB∥CD.
(2)解:∵AB∥CD,
∴∠AGH+∠CHG=180°,即∠AGM+∠MGH+∠MHG+∠MHC=180°,
∵∠MGH+∠MHG+∠GMH=180°,
∴∠GMH=∠AGM+∠MHC,
∵∠AGM=32°,∠MHC=68°,
∴∠GMH=100°.
(3)解:∠QHN的度数不发生改变,理由如下,
由(2)得,∠AGM+∠MHC=∠GMH=100°,
∴∠MGH+∠MHG=80°,
∵GP、HQ分别平分∠MGA和∠MHD,
∴∠MGP∠MGA,∠MHQ∠MHD(180°﹣∠MHC)=90°∠MHC,
∴∠PGH=∠MGP+∠MGH∠MGA+∠MGH,
∵HN∥PG,
∴∠GHN=∠PGH∠MGA+∠MGH,
∴∠QHN=∠GHN﹣∠GHQ=(∠MGA+∠MGH)﹣(∠MHQ﹣∠MHG)∠MGA+∠MGH﹣∠MHQ+∠MHG∠MGA+80°﹣∠MHQ,
∴∠QHN∠MGA+80°﹣(90°∠MHC)=﹣10°(∠MGA+∠MHC)=﹣10°100°=40°.
22.【思路点拨】
(1)通过证明∠DBF=∠EFG,利用同位角相等,两直线平行即可得出结论;
(2)过点E作GH∥BD,交AD于点H,利用(1)的结论和平行线的性质即可得出结论;
(3)设∠BDM=∠MDG=α,则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α,∠PDM=180°﹣α;利用已知条件用含α的式子表示∠PDN,∠EDN,∠GDN,∠DNG,再利用∠B﹣∠DNG=∠EDN,得到关于α的方程,解方程求得α的值,则∠B=180°﹣4α,结论可求.
【解题过程】
证明:(1)∵DG平分∠BDE,
∴∠BDG=∠ADG.
又∵∠BDG=∠BGD,
∴∠ADG=∠DGB.
∴AD∥BC.
∴∠DEF=∠EFG.
∵∠DBF=∠DEF,
∴∠DBF=∠EFG.
∴BD∥EF.
(2)过点G作GH∥BD,交AD于点H,如图,
∵BD∥EF,
∴GH∥EF.
∴∠BDG=∠DGH,∠GEF=∠HGE,
∵∠DGE=∠DGH+∠HGE,
∴∠DGE=∠BDG+∠FEG.
(3)设∠BDM=∠MDG=α,
则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α.
∴∠PDM=180°﹣α.
∵DN平分∠PDM
∴.
∴.
∴∠GDN=∠MDN﹣∠MDG=90°α=90°.
∵DG⊥ON,
∴∠DNG=90°.
∴.
∵DE∥BF,
∴∠B=∠PDE=180°﹣4α.
∵∠B﹣∠DNG=∠EDN,
∴,
解得:α=30°.
∴∠B=180°﹣4α=60°
21世纪教育网(www.21cnjy.com)
