湖南省怀化市2021-2022学年度高一下学期入学考试数学试题(Word版,含解析)
文档属性
| 名称 | 湖南省怀化市2021-2022学年度高一下学期入学考试数学试题(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 534.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 21:41:23 | ||
图片预览




文档简介
湖南省怀化市高一下学期入学考试数学试题
一、单选题
1.已知,,则等于( )
A. B. C.(0,2) D.(1,2)
2.已知函数f(x)是定义在R上的偶函数,且在[0,+∞)上单调递减,f(2)=0,则不等式f(log2x)>0的解集为( )
A.(,4) B.(2,2) C.(,+∞) D.(4,+∞)
3.直线l:x-y=1与圆C:x2+y2-4x=0的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
4.( ).A. B. C. D.
5.已知函数f(x)=a+log2(x2+a)(a>0)的最小值为8,则实数a的取值属于以下哪个范围( )
A.(5,6) B.(7,8) C.(8,9) D.(9,10)
6.将函数y=sin2x的图象向左平移(>0)个单位,得到的图象恰好关于直线对称,则的一个值是( )
A. B. C. D.
7.已知,则( )
A. B. C. D.
8.直线的倾斜角的取值范围是( )
A. B.
C. D.
9.若,则
A. B. C. D.
10.椭圆的焦点为,点为椭圆上的动点若为钝角,点的横坐标的取值范围为( )
A. B. C. D.
二、填空题
11.大于且终边与角重合的负角是________.
12.为了解网课学习效果,组织了一次网上测试.并利用分层抽样的方法从高中3个年级的学生中随机抽取了150人的测试成绩,其中高一、高二年级各抽取了40人,50人,若高三年级有学生1200人,则该高中共有学生_________人.
13.已知,,则__________.
14.已知函数,则______.
15.(2016年苏州11)已知角的终边经过点,则______.
三、解答题
16.已知直线l1:x+y+2=0,直线l2在y轴上的截距为-1,且l1⊥l2.
(1)求直线l1与l2的交点坐标;
(2)已知直线l3经过l1与l2的交点,且在y轴上的截距是在x轴上的截距的3倍,求l3的方程.
17.已知函数,.
(1)证明函数为奇函数;
(2)判断函数的单调性(无需证明),并求函数的值域;
(3)是否存在实数,使得的最大值为?若存在,求出的取值范围;若不存在,请说明理由.
18.在长方体中,,过、、三点的平面截去长方体的一个角后,得到如图所示的几何体,且这个几何体的体积为.
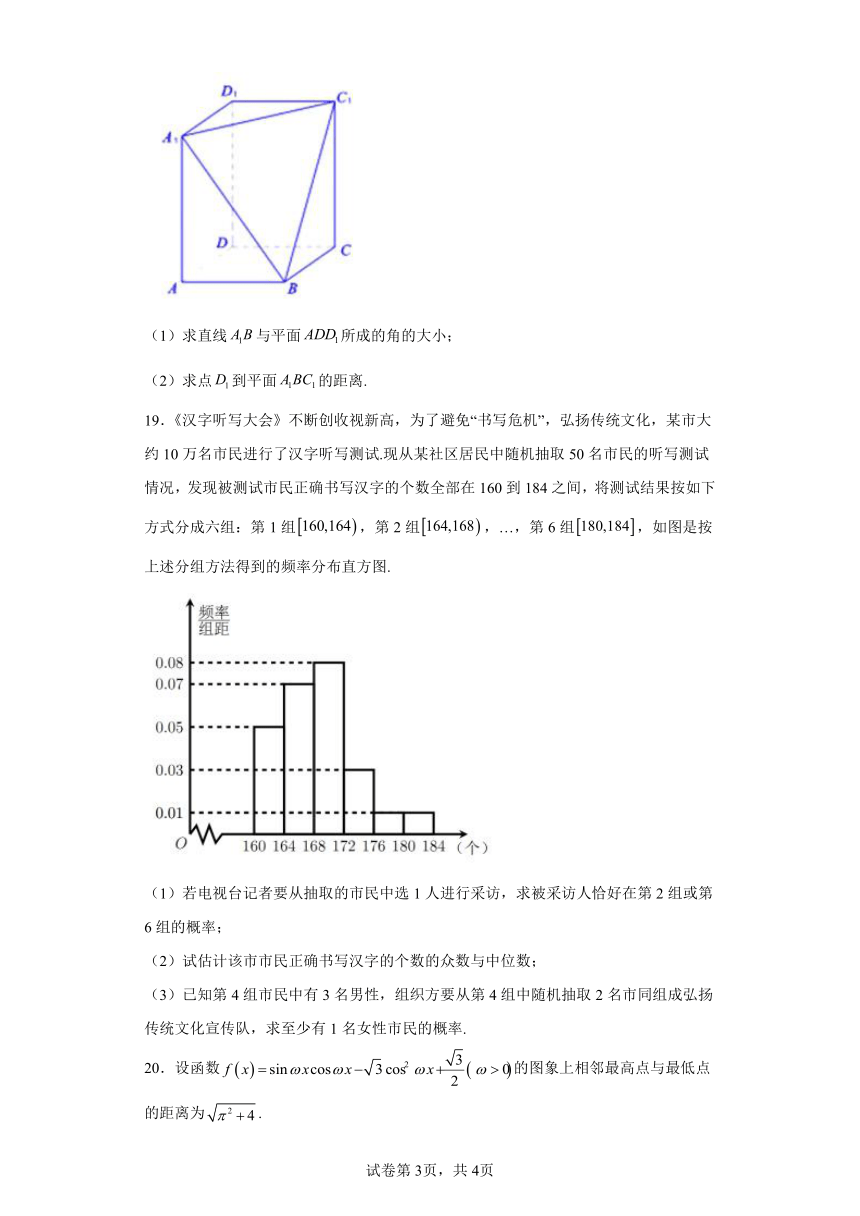
(1)求直线与平面所成的角的大小;
(2)求点到平面的距离.
19.《汉字听写大会》不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组,第2组,…,第6组,如图是按上述分组方法得到的频率分布直方图.
(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
(2)试估计该市市民正确书写汉字的个数的众数与中位数;
(3)已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市同组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
20.设函数的图象上相邻最高点与最低点的距离为.
(1)求的值;
(2)若函数是奇函数,求函数的单调递减区间.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
化简集合B,再进行并集运算.
【详解】
因为
所以
故选:B
【点睛】
本题主要考查了集合间的并集运算以及求定义域,属于基础题.
2.A
【解析】
【分析】
根据题意,由函数f(x)的奇偶性与f(2)=0可得f(log2x)>0 f(|log2x|)>f(2),结合函数f(x)的单调性分析可原不等式等价于|log2x|<2,解可得x的取值范围,即可得答案.
【详解】
根据题意,函数f(x)是定义在R上的偶函数,且f(2)=0,
则f(log2x)>0 f(|log2x|)>f(2),
又由f(x)在[0,+∞)上单调递减,f(|log2x|)>f(2) |log2x|<2,
变形可得:﹣2<log2x<2,
解得:x<2,不等式的解集为(,2);
故选:A.
【点睛】
本题主要考查函数的性质,利用函数的性质求解不等式,通常利用数形结合的方法求解,侧重考查数学抽象的核心素养.
3.C
【解析】
【详解】
圆C:x2+y2-4x=0,即.圆心为(2,0),半径为2.
圆心到直线的距离为:.
所以直线与圆相交,故选C.
点睛:对于直线和圆的位置关系的问题,可用“代数法”或“几何法”求解,直线与圆的位置关系体现了圆的几何性质和代数方法的结合,“代数法”与“几何法”是从不同的方面和思路来判断的,解题时不要单纯依靠代数计算,若选用几何法可使得解题过程既简单又不容易出错.
4.A
【解析】
由即可求出.
【详解】
.
故选:A.
5.A
【解析】
【分析】
根复合函数的单调性,得到函数f(x)的单调性,求解函数的最小值f(x)min=8,构造新函数g(a)=a+log2a-8,利用零点的存在定理,即可求解.
【详解】
由题意,根复合函数的单调性,可得函数f(x)在[0,+∞)上是增函数,在(-∞,0)上递减,
所以函数f(x)的最小值f(x)min=f(0)=a+log2a=8,
令g(a)=a+log2a-8,a>0,
则g(5)=log25-3<0,g(6)=log26-2>0,
又g(a)在(0,+∞)上是增函数,
所以实数a所在的区间为(5,6).
【点睛】
本题主要考查了函数的单调性的应用,以及零点的存在定理的应用,其中解答中根据复合函数的单调性,求得函数的最小值,构造新函数,利用零点的存在定理求解是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.
6.A
【解析】
【分析】
根据左加右减,写出三角函数平移后的解析式,根据平移后图象的对称轴,把对称轴代入使得函数式的值等于±1,写出自变量的值,根据求最小值得到结果.
【详解】
∵把函数y=sin2x的图象向左平移(>0)个单位,
∴平移后函数的解析式是 ,
∵所得图象关于直线 对称,
∴由正弦函数的图象和性质可得:
解得:
∴当 时,的最小值是.
故选A.
【点睛】
本题考查由三角函数图象的平移求函数的解析式,本题解题的关键是先表示出函数的解析式,再根据题意来写出结果,属于基础题.
7.A
【解析】
【分析】
根据正弦的和角公式展开,再运用辅助角公式得,再由根据诱导公式可得出所求的值.
【详解】
由,得
,所以,
,
故选:A.
【点睛】
本题考查正弦函数的和角公式,辅助角公式和三角函数的诱导公式,在解决给值求值的问题时,关键需找出待求的角与已知角的特殊关系,属于基础题.
8.B
【解析】
根据直线方程求出直线的斜率,再由的范围即可求解.
【详解】
直线2xcos α-y-3=0的斜率k=2cos α,
因为α∈,所以≤≤,
因此k=2cos α∈.
设直线的倾斜角为θ,则有tan θ∈.
又θ∈[0,π),且正切函数在上单调递增,在上为单调递增函数,
结合正切函数的图像可知
所以θ∈,即倾斜角的取值范围是.
故选:B
【点睛】
本题考查了直线的斜率与倾斜角,需熟记直线的斜率与倾斜角的关系,属于基础题.
9.B
【解析】
求解出集合,根据交集定义得到结果.
【详解】
本题正确选项:
【点睛】
本题考查集合运算中的交集运算,属于基础题.
10.B
【解析】
【分析】
根据椭圆方程,得到,,设,根据为钝角,推出,再由集合椭圆的方程,即可求出结果.
【详解】
因为,为椭圆的两焦点,则,,
设,则,,
因为为钝角,
所以,
又∵,∴,
∴.
故选:B.
【点睛】
本题主要考查求椭圆上点的横坐标的范围,涉及向量数量积的坐标表示,属于常考题型.
11.
【解析】
【分析】
根据终边相同的角的概念进行判断.
【详解】
大于且终边与角重合的负角是.
故答案为:
【点睛】
本题考查终边相同的角,属于基础题.
12.3000
【解析】
先求出高三年级抽取的人数为60人,由分层抽样的性质可得答案.
【详解】
由已知高三年级抽取的学生人数为:人.
设该校高中的学生总数为,则,解得
所以该高中共有学生3000
故答案为:3000
13.
【解析】
【分析】
根据已知条件和正弦的二倍角公式,求得,再利用诱导公式、同角三角函数的平方关系和象限角的符号,即可求得的值.
【详解】
∵,即,
∴,
∵,∴.
∴.
故答案为.
【点睛】
本题考查正弦函数的二倍角公式、同角三角函数的平方关系以及三角函数的符号与位置关系,属于三角函数求值问题中的“给值求值”问题.
14..
【解析】
【分析】
根据分段函数的解析式,代入准确运算,即可求解.
【详解】
由题意,函数,可得,
所以.
故答案为:
15.
【解析】
【详解】
由题意可得:,且:.
16.(1)
(2)或
【解析】
【分析】
(1)由直线的垂直关系可设设的方程为,根据纵截距求得的值,得到直线的方程,然后解方程组求得交点坐标;
(2)要考虑到直线l3经过经过原点和不经过原点的两种情况,结合直线方程的截距式求解即可.
(1)
解:设的方程为,
因为在y轴上的截距为,
所以,解得,
所以.
由,得,
所以直线与的交点坐标为.
(2)
解:①当过原点时,的方程为.
②当不过原点时,设的方程为.
又直线经过与的交点,
所以,解得,
则的方程为.
综上,的方程为或.
17.(1)证明见解析;(2) 在上单调递增,值域为 (3)
【解析】
【分析】
(1)证明函数为奇函数,首先判断定义域是否关于原点对称.奇函数还要满足.
(2)可通过改变函数单调性两个因素:取倒数和负号.较易判断单调性.单调性知道后值域就在端点出取得.
(3)首先令进行换元,注意换元后的定义域,将带有根式的函数换元成二次函数进行求解即可.
【详解】
(1),
的定义域为
又
奇函数.
(2)判断:在上单调递增
在上单调递增
,的值域为
(3)
令
则,
①时,在单调递增,
时,(符合题意)
②时,开口向下,对称轴,
当,即时,时,
;
当,即时,时,(符合题意)
③时,开口向上,对称轴,
当时,(符合题意)
综上:.
【点睛】
此题考查奇偶性的判断,根据改变函数单调性的两个因素判断函数单调性,单调函数值域求法,带根号函数换元处理成二次函数求解,属于一般性题目.
18.(1);(2)
【解析】
【分析】
设长方体高为,由长方体体积减去截掉的三棱锥体积可得几何体体积,由此建立方程求得;
(1)根据直线与平面所成角定义可知即为所求角,由可得结果;
(2)设所求距离为,由等体积法可知,由此构造关于的方程,解方程求得结果.
【详解】
设长方体的高
则几何体体积:,解得:
(1)平面 直线与平面所成角即为
所求线面夹角为:
(2)设点到平面的距离为
则由得:
为等腰三角形,,
高为
又 ,解得:
即点到面的距离为
【点睛】
本题考查立体几何中直线与平面所成角、点到面的距离的求解问题;立体几何中求解点到面的距离常采用等体积法,将问题转化为三棱锥高的求解,从而利用等体积转化构造方程求得结果,属于常考题型.
19.(1)0.32 ;(2)众数是170,中位数是168.25 ;(3)
【解析】
【分析】
(1)利用频率分布直方图能求出被采访人恰好在第2组或第6组的概率;
(2)利用频率分布直方图能求出众数和中位数;
(3)共50×0.12=6人,其中男生3人,设为a,b,c,女生三人,设为d,e,f,利用列举法能求出至少有1名女性市民的概率.
【详解】
(1)被采访人拾好在第2组或第6组的概率.
(2)众数:;
设中位数为,则
∴中位数.
(3)共人,其中男生3人,设为,,,女生三人,设为,,,则任选2人,
可能为,,,,,,,,,,,,,,,共15种,
其中两个全是男生的有,,,共3种情况,
设事件:至少有1名女性,则至少有1名女性市民的概率.
【点睛】
本题考查概率、众数、中位数的求法,考查频率分布直方图、列举法等基础知识,考查运算求解能力,属于基础题.
20.(1);
(2).
【解析】
【分析】
(1)利用三角恒等变换化简函数的解析式,可求得该函数的最小正周期以及最大值、最小值,由已知条件可得出关于的等式,即可求得正数的值;
(2)求出函数的表达式,利用该函数为奇函数可求得的值,然后利用余弦型函数的单调性可求得函数的单调递减区间.
(1)
解:
,
所以,函数的最小正周期为,
,,且函数的图象上相邻最高点与最低点的距离为,
则,所以,,解得,故.
(2)
解:为奇函数,
则,可得,,则,
所以,,
由,解得,
因此,函数的单调递减区间为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知,,则等于( )
A. B. C.(0,2) D.(1,2)
2.已知函数f(x)是定义在R上的偶函数,且在[0,+∞)上单调递减,f(2)=0,则不等式f(log2x)>0的解集为( )
A.(,4) B.(2,2) C.(,+∞) D.(4,+∞)
3.直线l:x-y=1与圆C:x2+y2-4x=0的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
4.( ).A. B. C. D.
5.已知函数f(x)=a+log2(x2+a)(a>0)的最小值为8,则实数a的取值属于以下哪个范围( )
A.(5,6) B.(7,8) C.(8,9) D.(9,10)
6.将函数y=sin2x的图象向左平移(>0)个单位,得到的图象恰好关于直线对称,则的一个值是( )
A. B. C. D.
7.已知,则( )
A. B. C. D.
8.直线的倾斜角的取值范围是( )
A. B.
C. D.
9.若,则
A. B. C. D.
10.椭圆的焦点为,点为椭圆上的动点若为钝角,点的横坐标的取值范围为( )
A. B. C. D.
二、填空题
11.大于且终边与角重合的负角是________.
12.为了解网课学习效果,组织了一次网上测试.并利用分层抽样的方法从高中3个年级的学生中随机抽取了150人的测试成绩,其中高一、高二年级各抽取了40人,50人,若高三年级有学生1200人,则该高中共有学生_________人.
13.已知,,则__________.
14.已知函数,则______.
15.(2016年苏州11)已知角的终边经过点,则______.
三、解答题
16.已知直线l1:x+y+2=0,直线l2在y轴上的截距为-1,且l1⊥l2.
(1)求直线l1与l2的交点坐标;
(2)已知直线l3经过l1与l2的交点,且在y轴上的截距是在x轴上的截距的3倍,求l3的方程.
17.已知函数,.
(1)证明函数为奇函数;
(2)判断函数的单调性(无需证明),并求函数的值域;
(3)是否存在实数,使得的最大值为?若存在,求出的取值范围;若不存在,请说明理由.
18.在长方体中,,过、、三点的平面截去长方体的一个角后,得到如图所示的几何体,且这个几何体的体积为.
(1)求直线与平面所成的角的大小;
(2)求点到平面的距离.
19.《汉字听写大会》不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组,第2组,…,第6组,如图是按上述分组方法得到的频率分布直方图.
(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
(2)试估计该市市民正确书写汉字的个数的众数与中位数;
(3)已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市同组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
20.设函数的图象上相邻最高点与最低点的距离为.
(1)求的值;
(2)若函数是奇函数,求函数的单调递减区间.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
化简集合B,再进行并集运算.
【详解】
因为
所以
故选:B
【点睛】
本题主要考查了集合间的并集运算以及求定义域,属于基础题.
2.A
【解析】
【分析】
根据题意,由函数f(x)的奇偶性与f(2)=0可得f(log2x)>0 f(|log2x|)>f(2),结合函数f(x)的单调性分析可原不等式等价于|log2x|<2,解可得x的取值范围,即可得答案.
【详解】
根据题意,函数f(x)是定义在R上的偶函数,且f(2)=0,
则f(log2x)>0 f(|log2x|)>f(2),
又由f(x)在[0,+∞)上单调递减,f(|log2x|)>f(2) |log2x|<2,
变形可得:﹣2<log2x<2,
解得:x<2,不等式的解集为(,2);
故选:A.
【点睛】
本题主要考查函数的性质,利用函数的性质求解不等式,通常利用数形结合的方法求解,侧重考查数学抽象的核心素养.
3.C
【解析】
【详解】
圆C:x2+y2-4x=0,即.圆心为(2,0),半径为2.
圆心到直线的距离为:.
所以直线与圆相交,故选C.
点睛:对于直线和圆的位置关系的问题,可用“代数法”或“几何法”求解,直线与圆的位置关系体现了圆的几何性质和代数方法的结合,“代数法”与“几何法”是从不同的方面和思路来判断的,解题时不要单纯依靠代数计算,若选用几何法可使得解题过程既简单又不容易出错.
4.A
【解析】
由即可求出.
【详解】
.
故选:A.
5.A
【解析】
【分析】
根复合函数的单调性,得到函数f(x)的单调性,求解函数的最小值f(x)min=8,构造新函数g(a)=a+log2a-8,利用零点的存在定理,即可求解.
【详解】
由题意,根复合函数的单调性,可得函数f(x)在[0,+∞)上是增函数,在(-∞,0)上递减,
所以函数f(x)的最小值f(x)min=f(0)=a+log2a=8,
令g(a)=a+log2a-8,a>0,
则g(5)=log25-3<0,g(6)=log26-2>0,
又g(a)在(0,+∞)上是增函数,
所以实数a所在的区间为(5,6).
【点睛】
本题主要考查了函数的单调性的应用,以及零点的存在定理的应用,其中解答中根据复合函数的单调性,求得函数的最小值,构造新函数,利用零点的存在定理求解是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.
6.A
【解析】
【分析】
根据左加右减,写出三角函数平移后的解析式,根据平移后图象的对称轴,把对称轴代入使得函数式的值等于±1,写出自变量的值,根据求最小值得到结果.
【详解】
∵把函数y=sin2x的图象向左平移(>0)个单位,
∴平移后函数的解析式是 ,
∵所得图象关于直线 对称,
∴由正弦函数的图象和性质可得:
解得:
∴当 时,的最小值是.
故选A.
【点睛】
本题考查由三角函数图象的平移求函数的解析式,本题解题的关键是先表示出函数的解析式,再根据题意来写出结果,属于基础题.
7.A
【解析】
【分析】
根据正弦的和角公式展开,再运用辅助角公式得,再由根据诱导公式可得出所求的值.
【详解】
由,得
,所以,
,
故选:A.
【点睛】
本题考查正弦函数的和角公式,辅助角公式和三角函数的诱导公式,在解决给值求值的问题时,关键需找出待求的角与已知角的特殊关系,属于基础题.
8.B
【解析】
根据直线方程求出直线的斜率,再由的范围即可求解.
【详解】
直线2xcos α-y-3=0的斜率k=2cos α,
因为α∈,所以≤≤,
因此k=2cos α∈.
设直线的倾斜角为θ,则有tan θ∈.
又θ∈[0,π),且正切函数在上单调递增,在上为单调递增函数,
结合正切函数的图像可知
所以θ∈,即倾斜角的取值范围是.
故选:B
【点睛】
本题考查了直线的斜率与倾斜角,需熟记直线的斜率与倾斜角的关系,属于基础题.
9.B
【解析】
求解出集合,根据交集定义得到结果.
【详解】
本题正确选项:
【点睛】
本题考查集合运算中的交集运算,属于基础题.
10.B
【解析】
【分析】
根据椭圆方程,得到,,设,根据为钝角,推出,再由集合椭圆的方程,即可求出结果.
【详解】
因为,为椭圆的两焦点,则,,
设,则,,
因为为钝角,
所以,
又∵,∴,
∴.
故选:B.
【点睛】
本题主要考查求椭圆上点的横坐标的范围,涉及向量数量积的坐标表示,属于常考题型.
11.
【解析】
【分析】
根据终边相同的角的概念进行判断.
【详解】
大于且终边与角重合的负角是.
故答案为:
【点睛】
本题考查终边相同的角,属于基础题.
12.3000
【解析】
先求出高三年级抽取的人数为60人,由分层抽样的性质可得答案.
【详解】
由已知高三年级抽取的学生人数为:人.
设该校高中的学生总数为,则,解得
所以该高中共有学生3000
故答案为:3000
13.
【解析】
【分析】
根据已知条件和正弦的二倍角公式,求得,再利用诱导公式、同角三角函数的平方关系和象限角的符号,即可求得的值.
【详解】
∵,即,
∴,
∵,∴.
∴.
故答案为.
【点睛】
本题考查正弦函数的二倍角公式、同角三角函数的平方关系以及三角函数的符号与位置关系,属于三角函数求值问题中的“给值求值”问题.
14..
【解析】
【分析】
根据分段函数的解析式,代入准确运算,即可求解.
【详解】
由题意,函数,可得,
所以.
故答案为:
15.
【解析】
【详解】
由题意可得:,且:.
16.(1)
(2)或
【解析】
【分析】
(1)由直线的垂直关系可设设的方程为,根据纵截距求得的值,得到直线的方程,然后解方程组求得交点坐标;
(2)要考虑到直线l3经过经过原点和不经过原点的两种情况,结合直线方程的截距式求解即可.
(1)
解:设的方程为,
因为在y轴上的截距为,
所以,解得,
所以.
由,得,
所以直线与的交点坐标为.
(2)
解:①当过原点时,的方程为.
②当不过原点时,设的方程为.
又直线经过与的交点,
所以,解得,
则的方程为.
综上,的方程为或.
17.(1)证明见解析;(2) 在上单调递增,值域为 (3)
【解析】
【分析】
(1)证明函数为奇函数,首先判断定义域是否关于原点对称.奇函数还要满足.
(2)可通过改变函数单调性两个因素:取倒数和负号.较易判断单调性.单调性知道后值域就在端点出取得.
(3)首先令进行换元,注意换元后的定义域,将带有根式的函数换元成二次函数进行求解即可.
【详解】
(1),
的定义域为
又
奇函数.
(2)判断:在上单调递增
在上单调递增
,的值域为
(3)
令
则,
①时,在单调递增,
时,(符合题意)
②时,开口向下,对称轴,
当,即时,时,
;
当,即时,时,(符合题意)
③时,开口向上,对称轴,
当时,(符合题意)
综上:.
【点睛】
此题考查奇偶性的判断,根据改变函数单调性的两个因素判断函数单调性,单调函数值域求法,带根号函数换元处理成二次函数求解,属于一般性题目.
18.(1);(2)
【解析】
【分析】
设长方体高为,由长方体体积减去截掉的三棱锥体积可得几何体体积,由此建立方程求得;
(1)根据直线与平面所成角定义可知即为所求角,由可得结果;
(2)设所求距离为,由等体积法可知,由此构造关于的方程,解方程求得结果.
【详解】
设长方体的高
则几何体体积:,解得:
(1)平面 直线与平面所成角即为
所求线面夹角为:
(2)设点到平面的距离为
则由得:
为等腰三角形,,
高为
又 ,解得:
即点到面的距离为
【点睛】
本题考查立体几何中直线与平面所成角、点到面的距离的求解问题;立体几何中求解点到面的距离常采用等体积法,将问题转化为三棱锥高的求解,从而利用等体积转化构造方程求得结果,属于常考题型.
19.(1)0.32 ;(2)众数是170,中位数是168.25 ;(3)
【解析】
【分析】
(1)利用频率分布直方图能求出被采访人恰好在第2组或第6组的概率;
(2)利用频率分布直方图能求出众数和中位数;
(3)共50×0.12=6人,其中男生3人,设为a,b,c,女生三人,设为d,e,f,利用列举法能求出至少有1名女性市民的概率.
【详解】
(1)被采访人拾好在第2组或第6组的概率.
(2)众数:;
设中位数为,则
∴中位数.
(3)共人,其中男生3人,设为,,,女生三人,设为,,,则任选2人,
可能为,,,,,,,,,,,,,,,共15种,
其中两个全是男生的有,,,共3种情况,
设事件:至少有1名女性,则至少有1名女性市民的概率.
【点睛】
本题考查概率、众数、中位数的求法,考查频率分布直方图、列举法等基础知识,考查运算求解能力,属于基础题.
20.(1);
(2).
【解析】
【分析】
(1)利用三角恒等变换化简函数的解析式,可求得该函数的最小正周期以及最大值、最小值,由已知条件可得出关于的等式,即可求得正数的值;
(2)求出函数的表达式,利用该函数为奇函数可求得的值,然后利用余弦型函数的单调性可求得函数的单调递减区间.
(1)
解:
,
所以,函数的最小正周期为,
,,且函数的图象上相邻最高点与最低点的距离为,
则,所以,,解得,故.
(2)
解:为奇函数,
则,可得,,则,
所以,,
由,解得,
因此,函数的单调递减区间为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
