云南省昆明市官渡区2021-2022学年度高一下学期开学考试数学试题(Word版,含解析)
文档属性
| 名称 | 云南省昆明市官渡区2021-2022学年度高一下学期开学考试数学试题(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 842.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 21:48:09 | ||
图片预览




文档简介
云南省昆明市官渡区高一下学期开学考试数学试题
一、单选题
1.已知,,则( )
A. B. C. D.
2.自古以来,人们对于崇山峻岭都心存敬畏,同时感慨大自然的鬼斧神工,一代诗圣杜甫曾赋诗《望岳》:“岱宗夫如何?齐鲁青未了.造化钟神秀,阴阳割昏晓.荡胸生层云,决毗入归鸟.会当凌绝顶,一览众山小.”然而,随着技术手段的发展,山高路远便不再人们出行的阻碍,伟大领袖毛主席曾作词:“桥飞架南北,天堑变通途”.在科技腾飞的当下,路桥建设部门仍然潜心研究如何缩短空间距离方便出行,如港珠澳跨海大桥等.如图为某工程队将A到D修建条隧道,测量员测得些数据如图所示(A,B,C,D在同一水平面内),则A,D间的距离为( )
A.km B.km C.km D.km
3.在中,,则角等于( )
A. B. C. D.
4.已知函数,若,且,则取最大值时的值为
A. B.
C. D.
5.已知函数既是二次函数又是幂函数,函数,函数,则的值为( )
A.0 B.20 C.80 D.82
6.在流行病学中,基本传染数R0是指在没有外力介入,同时所有人都没有免疫力的情况下,一个感染者平均传染的人数.初始感染者传染R0个人,为第一轮传染,这R0个人中每人再传染R0个人,为第二轮传染,…….R0一般由疾病的感染周期 感染者与其他人的接触频率 每次接触过程中传染的概率决定.假设新冠肺炎的基本传染数,平均感染周期为7天,设某一轮新增加的感染人数为M,则当M>1000时需要的天数至少为( )参考数据:lg38≈1.58
A.34 B.35 C.36 D.37
7.若,则a,b,c的大小关系是( )
A. B. C. D.
8.若命题:“,”为真命题,则的取值范围是( )
A. B. C. D.
9.下列各式中,值为的是( )
A. B. C. D.
10.已知函数y=f(x)(x∈R)的图像如图所示,给出下列四个命题:
p1:函数y=f(x)满足f(-x)=-f(x);
p2:函数y=f(x)满足f(x+2)=f(-x);
p3:函数y=f(x)满足f(x)=f(-x);
p4:函数y=f(x)满足f(x+2)=f(x),
其中的真命题是( )
A.p1,p3 B.p2,p4
C.p1,p2 D.p3,p4
11.将函数,且,下列说法错误的是( )
A.为偶函数 B.
C.若在上单调递减,则的最大值为9 D.当时,在上有3个零点
12.已知向量,不共线,且向量与共线,则实数的值为( )
A.-2或-1 B.-2或1 C.-1或2 D.1或2
二、填空题
13.在中,,,有下述四个结论:
①若为的重心,则
②若为边上的一个动点,则为定值2
③若,为边上的两个动点,且,则的最小值为
④已知为内一点,若,且,则的最大值为2
其中所有正确结论的编号是______.
14.已知函数的图象关于直线对称,当时,,当时,,则(8)______.
15.已知函数满足,则__________.
16.设是等差数列的前项和,若,则__________.
三、解答题
17.已知等差数列满足,的前项和为.
(1)求及;
(2)记,求
18.已知中,角A,B,C所对的边分别为a,b,c,满足.
(1)求B的大小;
(2)如图,,在直线的右侧取点D,使得,求四边形面积的最大值.
19.已知函数,,.
(1)求函数的值域;
(2)若函数在区间上为增函数,求实数的取值范围.
20.已知是递增数列,其前项和为,,且,.
(Ⅰ)求数列的通项;
(Ⅱ)是否存在使得成立?若存在,写出一组符合条件的的值;若不存在,请说明理由;
(Ⅲ)设,若对于任意的,不等式
恒成立,求正整数的最大值.
21.已知非零向量与不共线,.
(1)若,求t的值;
(2)若A、B、C三点共线,求t的值.
22.已知二次函数满足以下条件:①经过原点②,③函数只有一个零点
(1)求二次函数的解析式;
(2)若对任意,恒成立,求实数m的取值范围:
(3)若函数与的图象有两个公共点,求实数t的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
根据并集定义计算,
【详解】
,,,
故选:D.
【点睛】
本题考查集合的交集运算,属于简单题.
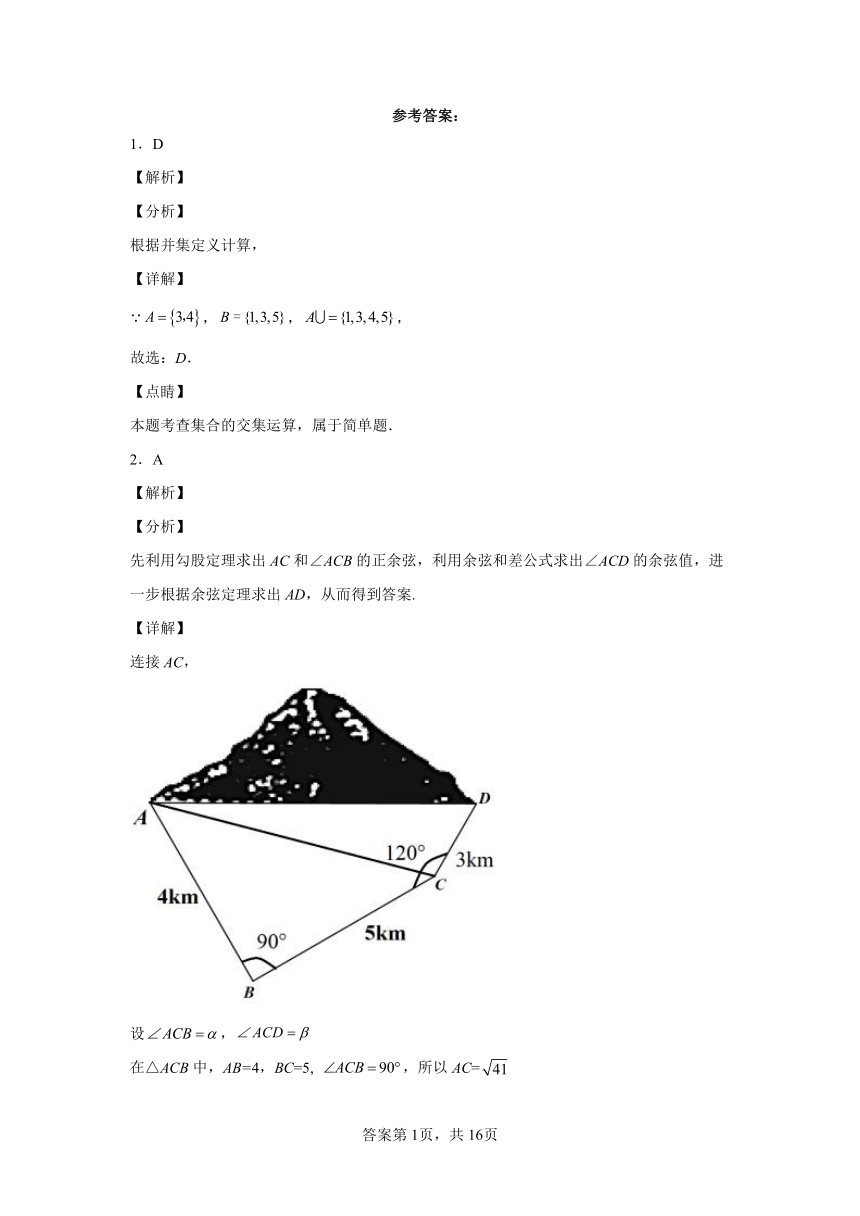
2.A
【解析】
【分析】
先利用勾股定理求出AC和∠ACB的正余弦,利用余弦和差公式求出∠ACD的余弦值,进一步根据余弦定理求出AD,从而得到答案.
【详解】
连接AC,
设,
在△ACB中,AB=4,BC=5, ,所以AC=
所以,
所以cos=
所以
多以.
故选:A.
【点睛】
本题考查利用余弦定理解决实际问题的知识点,考查计算能力,属于比较常见的题型.
3.D
【解析】
根据,利用求解.
【详解】
因为,
所以,
因为,
所以.
故选:D
【点睛】
本题主要考查两角和正切公式的变形应用,还考查运算求解的能力,属于中档题.
4.C
【解析】
根据可求得的范围;利用可知关于对称,从而可得的取值;二者结合求得,代入函数解析式,令解出即为结果.
【详解】
由得:,即:
由得:关于对称
,又
当,即时,取最大值
本题正确选项:
【点睛】
本题考查根据三角函数的性质求解函数解析式、根据函数的最值求解自变量取值的问题,关键是能够判断出函数的对称轴,并能够根据函数值的大小关系得到的范围.
5.D
【解析】
【分析】
根据和的性质可以判断关于中心对称,所求的函数值之和可根据对称性求解
【详解】
因为函数既是二次函数又是幂函数,所以函数,又,所以是奇函数,,因为,所以关于中心对称,
所以,故选:D
6.D
【解析】
假设第轮感染人数为,根据条件构造等比数列并写出其通项公式,根据题意列出关于的不等式,求解出结果,从而可确定出所需要的天数.
【详解】
设第轮感染人数为,则数列为等比数列,其中,公比为,
所以,解得,
而每轮感染周期为7天,所以需要的天数至少为.
故选:D.
【点睛】
关键点点睛:解答本题的关键点有两个:(1)理解题意构造合适的等比数列;(2)对数的计算.
7.D
【解析】
【分析】
,利用指数函数的单调性即可比较,再利用中间量法即可与比较,从而可得答案.
【详解】
解:,
因为函数在上时减函数,且
所以,
又,
所以.
故选:D.
8.C
【解析】
【分析】
分类讨论,时满足题意,时利用二次函数的性质求解.
【详解】
时,不等式为恒成立,
时,由题意得,解得,
综上的取值范围是.
故选:C.
【点睛】
本题考查一元二次不等式恒成立问题,掌握二次函数性质是解题关键,解题时注意对最高次系数是否为0进行讨论,最高次项系数为0,不等式不是二次不等式,求解方法与二次不等式不相同.
9.D
【解析】
【分析】
本题可通过二倍角公式以及同角三角函数关系得出结果.
【详解】
,
,
,
,
故选:D.
10.C
【解析】
【分析】
根据函数图像判断出函数的奇偶性和周期,从而可确定选项.
【详解】
从函数图像上可以看出函数的图像关于原点对称,所以是奇函数,函数y=f(x)满足f(-x)=-f(x),p1为真命题,p3为假命题;从函数图像上可以看出函数的周期为4,由p2:f(x+2)=f(-x)=-f(x),即f(x+4)=f(x),知函数的周期为4,所以p2为真命题,p4为假命题,
故选C.
【点睛】
本题考查由函数图像确定函数的有关性质.
11.C
【解析】
【分析】
先求得,然后结合函数的奇偶性、单调性、零点对选项进行分析,从而确定正确选项.
【详解】
,
,
所以,为偶函数,A选项正确.
,B选项正确.
,若在上单调递减,
则,,
由于,所以,
所以的最大值为,的最大值为,C选项错误.
当时,,
,当时,,所以D选项正确.
故选:C
12.B
【解析】
【分析】
利用平面向量共线基本定理列等式,利用不共线向量相等列方程组求解.
【详解】
若向量与共线,则存在实数,使得
,
又因为向量,不共线,所以
,
解得或.
故选:B.
13.①③
【解析】
【分析】
易知三角形是等腰直角三角形,
①取BC的中点D,根据为的重心,利用平面向量的基本定理求解判断;②由在上的投影为求解判断;③以A为原点,分别以AB,AC为x,y轴,建立平面坐标系,易知直线BC的方程为,设,利用数量积运算求解判断;④设,,且,易得,再由,得到求解判断.
【详解】
在中,,,所以三角形是等腰直角三角形,
如图所示:
①取BC的中点D,因为为的重心,则,故正确;
②若为边上的一个动点,向量在上的投影为,所以,故错误;
③如图所示:
以A为原点,分别以AB,AC为x,y轴,建立平面坐标系,则,直线BC的方程为,,
因为,为边上的两个动点,设,且,不妨设,
因为,则 ,即,所以,
所以,当时,等号成立,所以的最小值为,故正确;
④如图所示:
,设,因为,所以,即,
设,且,又,
所以,
因为,所以,所以无最大值,则无最大值,故错误.
故答案为:①③
【点睛】
方法点睛:平面向量的基本运算方法是:一是基底法;二是坐标法.
14.1
【解析】
【分析】
由函数的图象关于直线对称,可求得,由时,,可求得,再结合当时,,可求得答案
【详解】
解:的图象关于对称,当时,,
,
当时,,
(8)(6)(4),
则(8),
故答案为:1.
15.1
【解析】
在中,令即可得解.
【详解】
因为,
所以,
故答案为:1
16.2
【解析】
【分析】
根据等差数列可知,代入可求得结果.
【详解】
由等差数列性质可知:
本题正确结果:
【点睛】
本题考查等差数列性质的应用,属于基础题.
17.(1),;(2).
【解析】
【分析】
(1)利用等差数列的通项公式,结合,可以得到两个关于首项和公差的二元一次方程,解这个方程组即可求出首项和公差,最后利用等差数列的通项公式 和前项和公式求出及;
(2)利用裂项相消法可以求出.
【详解】
1)设等差数列的公差为,
(2)由(1)知:
【点睛】
本题考查了等差数列的通项公式和前项和公式,考查了裂项相消法求数列前项和,考查了数学运算能力.
18.(1);(2).
【解析】
(1)由正弦定理将中的边化为角,再结合正弦的两角和公式化简可求得,从而得解;
(2)易知为等边三角形,在中,由余弦定理可求得,再根据和,可推出四边形的面积,最后由和正弦函数的图象与性质即可得解.
【详解】
解:(1)由正弦定理知,,
∵,
∴,
即,
∵,∴,
∵,∴.
(2)由(1)知,,
∵,∴为等边三角形,
在中,由余弦定理知,,
而,
,
∴四边形的面积,
∵,∴,
∴当即时,S取得最大值,为,
故四边形面积的最大值为.
【点睛】
解三角形的基本策略:一是利用正弦定理实现“边化角”,二是利用余弦定理实现“角化边”;求三角形面积的最大值也是一种常见类型,主要方法有两类,一是找到边之间的关系,利用基本不等式求最值,二是利用正弦定理,转化为关于某个角的函数,利用函数思想求最值.
19.(1);(2)
【解析】
【详解】
试题分析:(1),∵,∴,∴同理,∴∵,∴,∴由此可求出结果;(2)由(1)∵,,∴,令,;解之得,,则的单调递增区间为,,由已知,解之得,再根据,即可求出结果
试题解析:(1),∵
∴,∴
同理,∴
∵,∴,∴
∴
(2)由(1)
∵,,∴
令,;解之得,
则的单调递增区间为,,
由已知,解之得,
∵,∴,∴.
考点:1.由的部分图象确定其解析式;2.函数的值域;3.函数解析式的求解及常用方法.
20.(1)(2)不存在(3)8
【解析】
【详解】
(Ⅰ),得,解得,或.
由于,所以.
因为,所以.
故,
整理,得,即.
因为是递增数列,且,故,因此.
则数列是以2为首项,为公差的等差数列.
所以.………………………………………………5分
(Ⅱ)满足条件的正整数不存在,证明如下:
假设存在,使得,
则.
整理,得, ①
显然,左边为整数,所以①式不成立.
故满足条件的正整数不存在. ……………………8分
(Ⅲ),
不等式可转化为
.
设,
则
.
所以,即当增大时,也增大.
要使不等式对于任意的恒成立,只需即可.
因为,所以.
即.
所以,正整数的最大值为8. ………………………………………14分
21.(1)(2)
【解析】
【分析】
(1)由题意结合平面向量数乘的概念即可得解;
(2)由题意结合平面向量共线定理、平面向量线性运算法则可得,再由平面向量基本定理即可得解.
【详解】
(1)∵,∴,
∴,∵,∴,
∴;
(2)∵A、B、C三点共线,∴存在非零实数使,
∴即,
∴,
∵与不共线,∴,
∴.
【点睛】
本题考查了平面向量数乘的应用,考查了平面向量线性运算法则、共线定理及平面向量基本定理的应用,属于中档题.
22.(1);(2);(3).
【解析】
【分析】
(1)由题意可得,的最值为,且对称轴为,可设顶点式,又,代入可得的解析式;
(2)由参数分离可得对任意恒成立,令,则,则,,再由二次函数的最值求法,可得所求范围;
(3)由题意可得.此方程有两个实数根,令,,则关于的方程只有一个正实根,对的符号讨论,结合二次方程实根的分布,解不等式可得所求范围.
【详解】
(1)由条件②可知的对称轴为,由条件③可知的最值为,
可设顶点式,再根据,解得,
故解析式为.
(2)若对任意,恒成立,只需对任意恒成立,
即求在的最小值即可,
令,则,令,
所以,所以.
(3)由函数与的图象有两个公共点,即,整理得
.此方程有两个实数根,
令,,由m与x的图像关系知,当时,一个m对应两个x,
则关于m的方程只有一个正实数根,
分为以下三种情况:
若即时,,所以;
若即时,满足只有一个正实数根,有两种情况,
有2个相等的正实根或两异号根,即或
解得或,
综上所述,t的取值范围是.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知,,则( )
A. B. C. D.
2.自古以来,人们对于崇山峻岭都心存敬畏,同时感慨大自然的鬼斧神工,一代诗圣杜甫曾赋诗《望岳》:“岱宗夫如何?齐鲁青未了.造化钟神秀,阴阳割昏晓.荡胸生层云,决毗入归鸟.会当凌绝顶,一览众山小.”然而,随着技术手段的发展,山高路远便不再人们出行的阻碍,伟大领袖毛主席曾作词:“桥飞架南北,天堑变通途”.在科技腾飞的当下,路桥建设部门仍然潜心研究如何缩短空间距离方便出行,如港珠澳跨海大桥等.如图为某工程队将A到D修建条隧道,测量员测得些数据如图所示(A,B,C,D在同一水平面内),则A,D间的距离为( )
A.km B.km C.km D.km
3.在中,,则角等于( )
A. B. C. D.
4.已知函数,若,且,则取最大值时的值为
A. B.
C. D.
5.已知函数既是二次函数又是幂函数,函数,函数,则的值为( )
A.0 B.20 C.80 D.82
6.在流行病学中,基本传染数R0是指在没有外力介入,同时所有人都没有免疫力的情况下,一个感染者平均传染的人数.初始感染者传染R0个人,为第一轮传染,这R0个人中每人再传染R0个人,为第二轮传染,…….R0一般由疾病的感染周期 感染者与其他人的接触频率 每次接触过程中传染的概率决定.假设新冠肺炎的基本传染数,平均感染周期为7天,设某一轮新增加的感染人数为M,则当M>1000时需要的天数至少为( )参考数据:lg38≈1.58
A.34 B.35 C.36 D.37
7.若,则a,b,c的大小关系是( )
A. B. C. D.
8.若命题:“,”为真命题,则的取值范围是( )
A. B. C. D.
9.下列各式中,值为的是( )
A. B. C. D.
10.已知函数y=f(x)(x∈R)的图像如图所示,给出下列四个命题:
p1:函数y=f(x)满足f(-x)=-f(x);
p2:函数y=f(x)满足f(x+2)=f(-x);
p3:函数y=f(x)满足f(x)=f(-x);
p4:函数y=f(x)满足f(x+2)=f(x),
其中的真命题是( )
A.p1,p3 B.p2,p4
C.p1,p2 D.p3,p4
11.将函数,且,下列说法错误的是( )
A.为偶函数 B.
C.若在上单调递减,则的最大值为9 D.当时,在上有3个零点
12.已知向量,不共线,且向量与共线,则实数的值为( )
A.-2或-1 B.-2或1 C.-1或2 D.1或2
二、填空题
13.在中,,,有下述四个结论:
①若为的重心,则
②若为边上的一个动点,则为定值2
③若,为边上的两个动点,且,则的最小值为
④已知为内一点,若,且,则的最大值为2
其中所有正确结论的编号是______.
14.已知函数的图象关于直线对称,当时,,当时,,则(8)______.
15.已知函数满足,则__________.
16.设是等差数列的前项和,若,则__________.
三、解答题
17.已知等差数列满足,的前项和为.
(1)求及;
(2)记,求
18.已知中,角A,B,C所对的边分别为a,b,c,满足.
(1)求B的大小;
(2)如图,,在直线的右侧取点D,使得,求四边形面积的最大值.
19.已知函数,,.
(1)求函数的值域;
(2)若函数在区间上为增函数,求实数的取值范围.
20.已知是递增数列,其前项和为,,且,.
(Ⅰ)求数列的通项;
(Ⅱ)是否存在使得成立?若存在,写出一组符合条件的的值;若不存在,请说明理由;
(Ⅲ)设,若对于任意的,不等式
恒成立,求正整数的最大值.
21.已知非零向量与不共线,.
(1)若,求t的值;
(2)若A、B、C三点共线,求t的值.
22.已知二次函数满足以下条件:①经过原点②,③函数只有一个零点
(1)求二次函数的解析式;
(2)若对任意,恒成立,求实数m的取值范围:
(3)若函数与的图象有两个公共点,求实数t的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
根据并集定义计算,
【详解】
,,,
故选:D.
【点睛】
本题考查集合的交集运算,属于简单题.
2.A
【解析】
【分析】
先利用勾股定理求出AC和∠ACB的正余弦,利用余弦和差公式求出∠ACD的余弦值,进一步根据余弦定理求出AD,从而得到答案.
【详解】
连接AC,
设,
在△ACB中,AB=4,BC=5, ,所以AC=
所以,
所以cos=
所以
多以.
故选:A.
【点睛】
本题考查利用余弦定理解决实际问题的知识点,考查计算能力,属于比较常见的题型.
3.D
【解析】
根据,利用求解.
【详解】
因为,
所以,
因为,
所以.
故选:D
【点睛】
本题主要考查两角和正切公式的变形应用,还考查运算求解的能力,属于中档题.
4.C
【解析】
根据可求得的范围;利用可知关于对称,从而可得的取值;二者结合求得,代入函数解析式,令解出即为结果.
【详解】
由得:,即:
由得:关于对称
,又
当,即时,取最大值
本题正确选项:
【点睛】
本题考查根据三角函数的性质求解函数解析式、根据函数的最值求解自变量取值的问题,关键是能够判断出函数的对称轴,并能够根据函数值的大小关系得到的范围.
5.D
【解析】
【分析】
根据和的性质可以判断关于中心对称,所求的函数值之和可根据对称性求解
【详解】
因为函数既是二次函数又是幂函数,所以函数,又,所以是奇函数,,因为,所以关于中心对称,
所以,故选:D
6.D
【解析】
假设第轮感染人数为,根据条件构造等比数列并写出其通项公式,根据题意列出关于的不等式,求解出结果,从而可确定出所需要的天数.
【详解】
设第轮感染人数为,则数列为等比数列,其中,公比为,
所以,解得,
而每轮感染周期为7天,所以需要的天数至少为.
故选:D.
【点睛】
关键点点睛:解答本题的关键点有两个:(1)理解题意构造合适的等比数列;(2)对数的计算.
7.D
【解析】
【分析】
,利用指数函数的单调性即可比较,再利用中间量法即可与比较,从而可得答案.
【详解】
解:,
因为函数在上时减函数,且
所以,
又,
所以.
故选:D.
8.C
【解析】
【分析】
分类讨论,时满足题意,时利用二次函数的性质求解.
【详解】
时,不等式为恒成立,
时,由题意得,解得,
综上的取值范围是.
故选:C.
【点睛】
本题考查一元二次不等式恒成立问题,掌握二次函数性质是解题关键,解题时注意对最高次系数是否为0进行讨论,最高次项系数为0,不等式不是二次不等式,求解方法与二次不等式不相同.
9.D
【解析】
【分析】
本题可通过二倍角公式以及同角三角函数关系得出结果.
【详解】
,
,
,
,
故选:D.
10.C
【解析】
【分析】
根据函数图像判断出函数的奇偶性和周期,从而可确定选项.
【详解】
从函数图像上可以看出函数的图像关于原点对称,所以是奇函数,函数y=f(x)满足f(-x)=-f(x),p1为真命题,p3为假命题;从函数图像上可以看出函数的周期为4,由p2:f(x+2)=f(-x)=-f(x),即f(x+4)=f(x),知函数的周期为4,所以p2为真命题,p4为假命题,
故选C.
【点睛】
本题考查由函数图像确定函数的有关性质.
11.C
【解析】
【分析】
先求得,然后结合函数的奇偶性、单调性、零点对选项进行分析,从而确定正确选项.
【详解】
,
,
所以,为偶函数,A选项正确.
,B选项正确.
,若在上单调递减,
则,,
由于,所以,
所以的最大值为,的最大值为,C选项错误.
当时,,
,当时,,所以D选项正确.
故选:C
12.B
【解析】
【分析】
利用平面向量共线基本定理列等式,利用不共线向量相等列方程组求解.
【详解】
若向量与共线,则存在实数,使得
,
又因为向量,不共线,所以
,
解得或.
故选:B.
13.①③
【解析】
【分析】
易知三角形是等腰直角三角形,
①取BC的中点D,根据为的重心,利用平面向量的基本定理求解判断;②由在上的投影为求解判断;③以A为原点,分别以AB,AC为x,y轴,建立平面坐标系,易知直线BC的方程为,设,利用数量积运算求解判断;④设,,且,易得,再由,得到求解判断.
【详解】
在中,,,所以三角形是等腰直角三角形,
如图所示:
①取BC的中点D,因为为的重心,则,故正确;
②若为边上的一个动点,向量在上的投影为,所以,故错误;
③如图所示:
以A为原点,分别以AB,AC为x,y轴,建立平面坐标系,则,直线BC的方程为,,
因为,为边上的两个动点,设,且,不妨设,
因为,则 ,即,所以,
所以,当时,等号成立,所以的最小值为,故正确;
④如图所示:
,设,因为,所以,即,
设,且,又,
所以,
因为,所以,所以无最大值,则无最大值,故错误.
故答案为:①③
【点睛】
方法点睛:平面向量的基本运算方法是:一是基底法;二是坐标法.
14.1
【解析】
【分析】
由函数的图象关于直线对称,可求得,由时,,可求得,再结合当时,,可求得答案
【详解】
解:的图象关于对称,当时,,
,
当时,,
(8)(6)(4),
则(8),
故答案为:1.
15.1
【解析】
在中,令即可得解.
【详解】
因为,
所以,
故答案为:1
16.2
【解析】
【分析】
根据等差数列可知,代入可求得结果.
【详解】
由等差数列性质可知:
本题正确结果:
【点睛】
本题考查等差数列性质的应用,属于基础题.
17.(1),;(2).
【解析】
【分析】
(1)利用等差数列的通项公式,结合,可以得到两个关于首项和公差的二元一次方程,解这个方程组即可求出首项和公差,最后利用等差数列的通项公式 和前项和公式求出及;
(2)利用裂项相消法可以求出.
【详解】
1)设等差数列的公差为,
(2)由(1)知:
【点睛】
本题考查了等差数列的通项公式和前项和公式,考查了裂项相消法求数列前项和,考查了数学运算能力.
18.(1);(2).
【解析】
(1)由正弦定理将中的边化为角,再结合正弦的两角和公式化简可求得,从而得解;
(2)易知为等边三角形,在中,由余弦定理可求得,再根据和,可推出四边形的面积,最后由和正弦函数的图象与性质即可得解.
【详解】
解:(1)由正弦定理知,,
∵,
∴,
即,
∵,∴,
∵,∴.
(2)由(1)知,,
∵,∴为等边三角形,
在中,由余弦定理知,,
而,
,
∴四边形的面积,
∵,∴,
∴当即时,S取得最大值,为,
故四边形面积的最大值为.
【点睛】
解三角形的基本策略:一是利用正弦定理实现“边化角”,二是利用余弦定理实现“角化边”;求三角形面积的最大值也是一种常见类型,主要方法有两类,一是找到边之间的关系,利用基本不等式求最值,二是利用正弦定理,转化为关于某个角的函数,利用函数思想求最值.
19.(1);(2)
【解析】
【详解】
试题分析:(1),∵,∴,∴同理,∴∵,∴,∴由此可求出结果;(2)由(1)∵,,∴,令,;解之得,,则的单调递增区间为,,由已知,解之得,再根据,即可求出结果
试题解析:(1),∵
∴,∴
同理,∴
∵,∴,∴
∴
(2)由(1)
∵,,∴
令,;解之得,
则的单调递增区间为,,
由已知,解之得,
∵,∴,∴.
考点:1.由的部分图象确定其解析式;2.函数的值域;3.函数解析式的求解及常用方法.
20.(1)(2)不存在(3)8
【解析】
【详解】
(Ⅰ),得,解得,或.
由于,所以.
因为,所以.
故,
整理,得,即.
因为是递增数列,且,故,因此.
则数列是以2为首项,为公差的等差数列.
所以.………………………………………………5分
(Ⅱ)满足条件的正整数不存在,证明如下:
假设存在,使得,
则.
整理,得, ①
显然,左边为整数,所以①式不成立.
故满足条件的正整数不存在. ……………………8分
(Ⅲ),
不等式可转化为
.
设,
则
.
所以,即当增大时,也增大.
要使不等式对于任意的恒成立,只需即可.
因为,所以.
即.
所以,正整数的最大值为8. ………………………………………14分
21.(1)(2)
【解析】
【分析】
(1)由题意结合平面向量数乘的概念即可得解;
(2)由题意结合平面向量共线定理、平面向量线性运算法则可得,再由平面向量基本定理即可得解.
【详解】
(1)∵,∴,
∴,∵,∴,
∴;
(2)∵A、B、C三点共线,∴存在非零实数使,
∴即,
∴,
∵与不共线,∴,
∴.
【点睛】
本题考查了平面向量数乘的应用,考查了平面向量线性运算法则、共线定理及平面向量基本定理的应用,属于中档题.
22.(1);(2);(3).
【解析】
【分析】
(1)由题意可得,的最值为,且对称轴为,可设顶点式,又,代入可得的解析式;
(2)由参数分离可得对任意恒成立,令,则,则,,再由二次函数的最值求法,可得所求范围;
(3)由题意可得.此方程有两个实数根,令,,则关于的方程只有一个正实根,对的符号讨论,结合二次方程实根的分布,解不等式可得所求范围.
【详解】
(1)由条件②可知的对称轴为,由条件③可知的最值为,
可设顶点式,再根据,解得,
故解析式为.
(2)若对任意,恒成立,只需对任意恒成立,
即求在的最小值即可,
令,则,令,
所以,所以.
(3)由函数与的图象有两个公共点,即,整理得
.此方程有两个实数根,
令,,由m与x的图像关系知,当时,一个m对应两个x,
则关于m的方程只有一个正实数根,
分为以下三种情况:
若即时,,所以;
若即时,满足只有一个正实数根,有两种情况,
有2个相等的正实根或两异号根,即或
解得或,
综上所述,t的取值范围是.
答案第1页,共2页
答案第1页,共2页
同课章节目录
