2021—2022学年人教版八年级数学下册18.1.1平行四边形的性质课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.1.1平行四边形的性质课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 316.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 15:48:02 | ||
图片预览



文档简介
第十八章 平行四边形
18.1.1 平行四边形的性质
一、选择题
1.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD周长是( )
A.22 B.18 C.22或20 D.18或22
2.有下列说法:
①平行四边形具有四边形的所有性质:②平行四边形是中心对称图形:③平行四边形的任一条对角线可把平行四边形分成两个全等的三角形;④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形.
其中正确说法的序号是( ).A.①②④ B.①③④ C.①②③ D.①②③④
3.如图,平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
4.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=128°,则∠A=( )
A.32° B.42° C.52° D.62°
5.如图,在 ABCD中,∠D=80°,N是AD上一点,且AB=AN,则∠ANB的度数是( )
A.60° B.50° C.40° D.30°
6.如图,已知AOBC的顶点O(0,0),点B在x轴正半轴上,按以下步骤作图:
①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.若G的坐标为(2,4),则点A的坐标是( )
A.(﹣3,4) B.(﹣2,4) C. D.
7.如图,在中,,为对角线,将沿方向平移,使得与重合,点的对应点为点,过点作交的延长线于点,则下列说法正确的是( )
A. B.平分 C. D.
8.如图,在平行四边形中,对角线,相交于点,下列条说法不正确的是( )
A. B.
C. D.
9.如图, ABCD的对角线AC,BD相交于点O,则下列结论一定正确的是( )
A.OB=OD B.AB=BC C.AC⊥BD D.∠ABD=∠CBD
10.如图,中,对角线相交于点交于点,连接,若的周长为28,则的周长为( )
A.28 B.24 C.21 D.14
二、填空题
11.平行四边形ABCD中,∠ABC的平分线把AD分成5和7两部分,则平行四边形ABCD的周长为__.
12.如图,在平行四边形ABCD中,DE平分∠ADC,,,则平行四边形ABCD的周长是____.
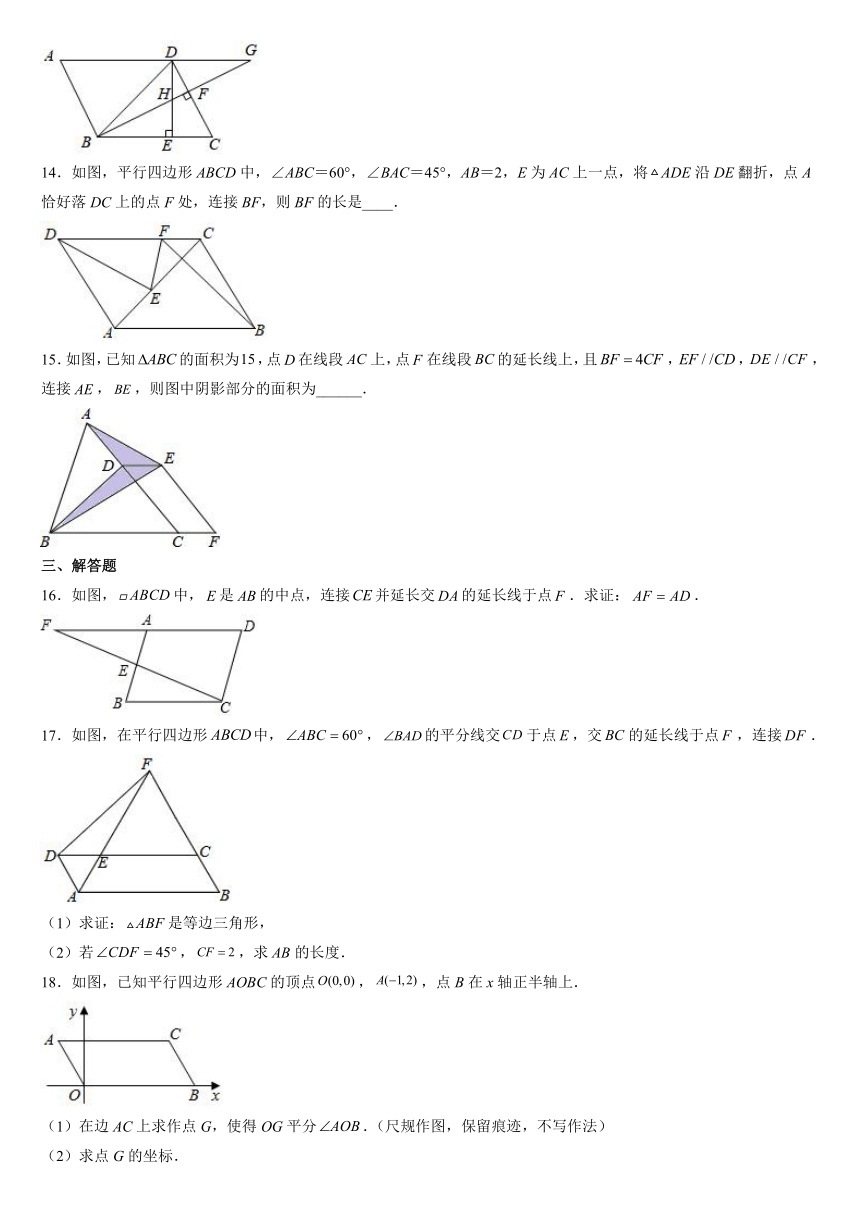
13.如图,在平行四边形ABCD中,DE⊥BC于点E,BF⊥CD于点F,DE和BF相交于点H,BF的延长线与AD的延长线相交于点G.若∠DBC=45°,现有以下四个说法:①BD=BE;②∠A=∠BHE;③△BCF≌△DCE;④AB=BH,则其中正确的是_____.
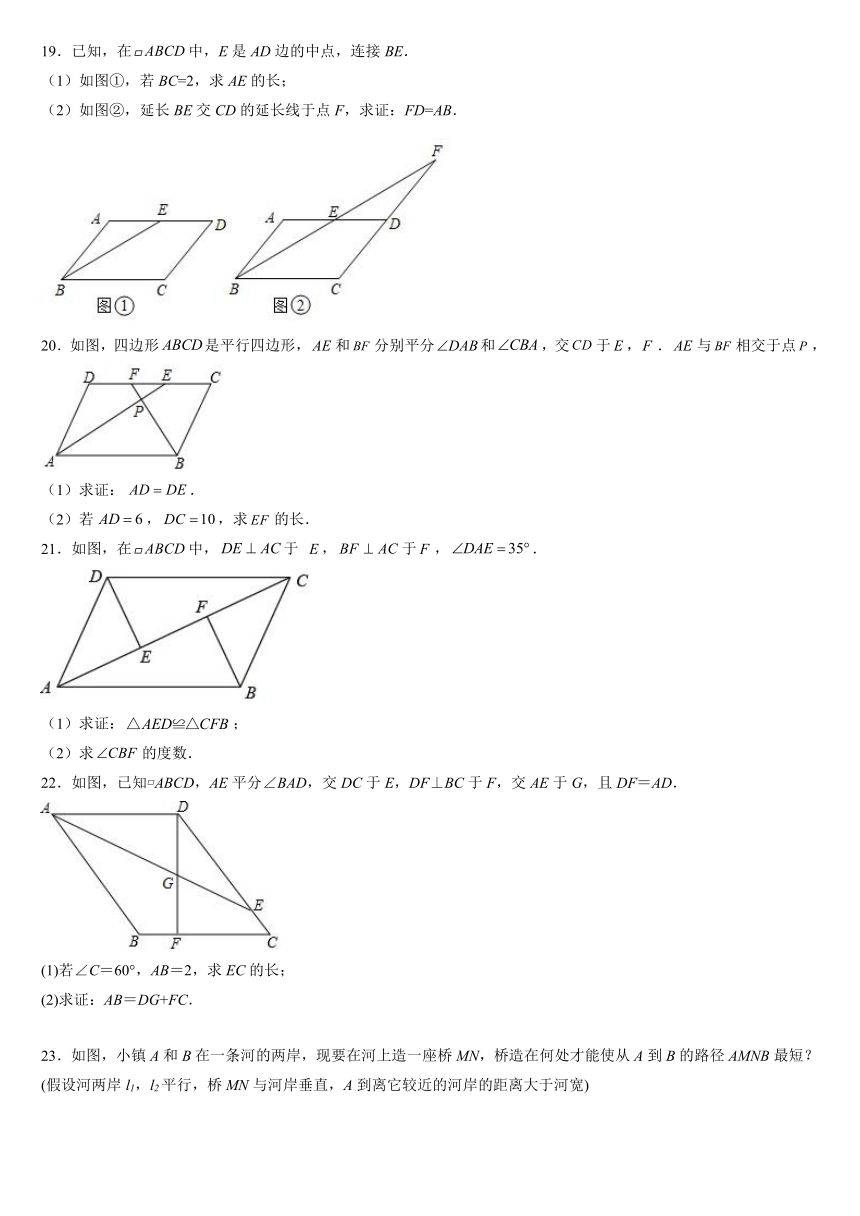
14.如图,平行四边形ABCD中,∠ABC=60°,∠BAC=45°,AB=2,E为AC上一点,将ADE沿DE翻折,点A恰好落DC上的点F处,连接BF,则BF的长是____.
15.如图,已知的面积为,点在线段上,点在线段的延长线上,且,,,连接,,则图中阴影部分的面积为______.
三、解答题
16.如图,中,是的中点,连接并延长交的延长线于点.求证:.
17.如图,在平行四边形中,,的平分线交于点,交的延长线于点,连接.
(1)求证:是等边三角形,
(2)若,,求的长度.
18.如图,已知平行四边形AOBC的顶点,,点B在x轴正半轴上.
(1)在边AC上求作点G,使得OG平分.(尺规作图,保留痕迹,不写作法)
(2)求点G的坐标.
19.已知,在中,E是AD边的中点,连接BE.
(1)如图①,若BC=2,求AE的长;
(2)如图②,延长BE交CD的延长线于点F,求证:FD=AB.
20.如图,四边形是平行四边形,和分别平分和,交于,.与相交于点,
(1)求证:.
(2)若,,求的长.
21.如图,在中,于 ,于,.
(1)求证:;
(2)求的度数.
22.如图,已知 ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
(1)若∠C=60°,AB=2,求EC的长;
(2)求证:AB=DG+FC.
23.如图,小镇A和B在一条河的两岸,现要在河上造一座桥MN,桥造在何处才能使从A到B的路径AMNB最短?(假设河两岸l1,l2平行,桥MN与河岸垂直,A到离它较近的河岸的距离大于河宽)
【参考答案】
1.C 2.D 3.B 4.C 5.C 6.A 7.D 8.C 9.A 10.D
11.34或38
12.28
13.①②④
14.2
15.5
16.证明:四边形是平行四边形,
,,
,
点为的中点,
,
在和中,
,
,
.
17.证明:(1)在平行四边形中,,,
∴
∵为的平分线
∴
又∵
∴是等边三角形
(2)过点作,如下图:
∵
∴,
∴为等边三角形
∴
∵
∴,
在中,,,
∴,
∵
∴
∴
∴
∴
18.解:(1)如图所示,以O为圆心,以任意长为半径画弧,分别交OA于E,OB于F,再分别以E、F为圆心,以大于EF长的一半为半径画弧,两者交于D,连接OD并延长,交AC于G,即为所求;
(2)∵四边形AOBC是平行四边形,
∴AC∥OB,
∴∠AGO=∠BOG,G的纵坐标与A相同
∵OG平分∠AOB,
∴∠AOG=∠BOG,
∴∠AOG=∠AGO,
∴AO=AG,
∵A( 1,2)
∴,
∴G的横坐标为,
∴.
19.(1)解:∵四边形ABCD是平行四边形,
∴BC=AD=2,
∵E是AD边的中点,
∴AE=1,
(2)证明:∵E为AD中点,
∴AE=DE,
∵四边形ABCD是平行四边形,
∴BA∥CD,
∴∠ABE=∠F
∵∠BEA=∠FED,
∴△ABE≌△DFE(AAS)
∴FD=AB.
20.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠DAE=∠DEA,
∴AD=DE;
(2)∵AD=6,DC=10,
∴DE=AD=6,
∴EC=DC-DE=10-6=4,
∵四边形ABCD是平行四边形,
∴AB∥DC,AD=BC=6,
∴∠CFB=∠FBA,
∵BF平分∠CBA,
∴∠CBF=∠FBA,
∴∠CFB=∠CBF,
∴BC=FC=6,
∴EF=FC-EC=6-4=2.
21.(1)证明:在平行四边形中,,
又,
,
,.
,
在和中,
(2)解:在中,, ,
.
22.(1)解:在中,,,,
∴,
∴,
在中,
,
.
,
∵,平分,
,,
,
;
(2)证明:如图所示:延长至,连接,使,
在和中,
,
,,
由(1)可得:
,
,即,
,
即.
18.1.1 平行四边形的性质
一、选择题
1.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD周长是( )
A.22 B.18 C.22或20 D.18或22
2.有下列说法:
①平行四边形具有四边形的所有性质:②平行四边形是中心对称图形:③平行四边形的任一条对角线可把平行四边形分成两个全等的三角形;④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形.
其中正确说法的序号是( ).A.①②④ B.①③④ C.①②③ D.①②③④
3.如图,平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
4.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=128°,则∠A=( )
A.32° B.42° C.52° D.62°
5.如图,在 ABCD中,∠D=80°,N是AD上一点,且AB=AN,则∠ANB的度数是( )
A.60° B.50° C.40° D.30°
6.如图,已知AOBC的顶点O(0,0),点B在x轴正半轴上,按以下步骤作图:
①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.若G的坐标为(2,4),则点A的坐标是( )
A.(﹣3,4) B.(﹣2,4) C. D.
7.如图,在中,,为对角线,将沿方向平移,使得与重合,点的对应点为点,过点作交的延长线于点,则下列说法正确的是( )
A. B.平分 C. D.
8.如图,在平行四边形中,对角线,相交于点,下列条说法不正确的是( )
A. B.
C. D.
9.如图, ABCD的对角线AC,BD相交于点O,则下列结论一定正确的是( )
A.OB=OD B.AB=BC C.AC⊥BD D.∠ABD=∠CBD
10.如图,中,对角线相交于点交于点,连接,若的周长为28,则的周长为( )
A.28 B.24 C.21 D.14
二、填空题
11.平行四边形ABCD中,∠ABC的平分线把AD分成5和7两部分,则平行四边形ABCD的周长为__.
12.如图,在平行四边形ABCD中,DE平分∠ADC,,,则平行四边形ABCD的周长是____.
13.如图,在平行四边形ABCD中,DE⊥BC于点E,BF⊥CD于点F,DE和BF相交于点H,BF的延长线与AD的延长线相交于点G.若∠DBC=45°,现有以下四个说法:①BD=BE;②∠A=∠BHE;③△BCF≌△DCE;④AB=BH,则其中正确的是_____.
14.如图,平行四边形ABCD中,∠ABC=60°,∠BAC=45°,AB=2,E为AC上一点,将ADE沿DE翻折,点A恰好落DC上的点F处,连接BF,则BF的长是____.
15.如图,已知的面积为,点在线段上,点在线段的延长线上,且,,,连接,,则图中阴影部分的面积为______.
三、解答题
16.如图,中,是的中点,连接并延长交的延长线于点.求证:.
17.如图,在平行四边形中,,的平分线交于点,交的延长线于点,连接.
(1)求证:是等边三角形,
(2)若,,求的长度.
18.如图,已知平行四边形AOBC的顶点,,点B在x轴正半轴上.
(1)在边AC上求作点G,使得OG平分.(尺规作图,保留痕迹,不写作法)
(2)求点G的坐标.
19.已知,在中,E是AD边的中点,连接BE.
(1)如图①,若BC=2,求AE的长;
(2)如图②,延长BE交CD的延长线于点F,求证:FD=AB.
20.如图,四边形是平行四边形,和分别平分和,交于,.与相交于点,
(1)求证:.
(2)若,,求的长.
21.如图,在中,于 ,于,.
(1)求证:;
(2)求的度数.
22.如图,已知 ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
(1)若∠C=60°,AB=2,求EC的长;
(2)求证:AB=DG+FC.
23.如图,小镇A和B在一条河的两岸,现要在河上造一座桥MN,桥造在何处才能使从A到B的路径AMNB最短?(假设河两岸l1,l2平行,桥MN与河岸垂直,A到离它较近的河岸的距离大于河宽)
【参考答案】
1.C 2.D 3.B 4.C 5.C 6.A 7.D 8.C 9.A 10.D
11.34或38
12.28
13.①②④
14.2
15.5
16.证明:四边形是平行四边形,
,,
,
点为的中点,
,
在和中,
,
,
.
17.证明:(1)在平行四边形中,,,
∴
∵为的平分线
∴
又∵
∴是等边三角形
(2)过点作,如下图:
∵
∴,
∴为等边三角形
∴
∵
∴,
在中,,,
∴,
∵
∴
∴
∴
∴
18.解:(1)如图所示,以O为圆心,以任意长为半径画弧,分别交OA于E,OB于F,再分别以E、F为圆心,以大于EF长的一半为半径画弧,两者交于D,连接OD并延长,交AC于G,即为所求;
(2)∵四边形AOBC是平行四边形,
∴AC∥OB,
∴∠AGO=∠BOG,G的纵坐标与A相同
∵OG平分∠AOB,
∴∠AOG=∠BOG,
∴∠AOG=∠AGO,
∴AO=AG,
∵A( 1,2)
∴,
∴G的横坐标为,
∴.
19.(1)解:∵四边形ABCD是平行四边形,
∴BC=AD=2,
∵E是AD边的中点,
∴AE=1,
(2)证明:∵E为AD中点,
∴AE=DE,
∵四边形ABCD是平行四边形,
∴BA∥CD,
∴∠ABE=∠F
∵∠BEA=∠FED,
∴△ABE≌△DFE(AAS)
∴FD=AB.
20.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠DAE=∠DEA,
∴AD=DE;
(2)∵AD=6,DC=10,
∴DE=AD=6,
∴EC=DC-DE=10-6=4,
∵四边形ABCD是平行四边形,
∴AB∥DC,AD=BC=6,
∴∠CFB=∠FBA,
∵BF平分∠CBA,
∴∠CBF=∠FBA,
∴∠CFB=∠CBF,
∴BC=FC=6,
∴EF=FC-EC=6-4=2.
21.(1)证明:在平行四边形中,,
又,
,
,.
,
在和中,
(2)解:在中,, ,
.
22.(1)解:在中,,,,
∴,
∴,
在中,
,
.
,
∵,平分,
,,
,
;
(2)证明:如图所示:延长至,连接,使,
在和中,
,
,,
由(1)可得:
,
,即,
,
即.
