2021-2022学年华东师大版九年级数学下册第27章 圆 单元测试训练卷(word版 含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册第27章 圆 单元测试训练卷(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 249.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 18:02:45 | ||
图片预览



文档简介
华东师大版九年级数学下册
第27章 圆
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列说法正确的是( )
A.平分弦的直径垂直于弦
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.若直线与圆有公共点,则直线与圆相切
2. 在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以点O为圆心,OA的长为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的树为( )
A.E、F、G B.F、G、H
C.G、H、E D.H、E、F
3. 如图,AB是⊙O的直径,D、C在⊙O上,AD∥OC,∠DAC=30°,连结AC,则∠BOC的度数为( )
A.30° B.60° C.45° D.80°
4. 如图,在△ABC中,∠BAC=28°,以AB为直径的⊙O交AC于点D,DE∥CB,连结BD,若添加一个条件,使BC是⊙O的切线,则下列四个条件中不符合的是( )
A.DE⊥AB B.∠EDB=28°
C.∠ADE=∠ABD D.OB=BC
5. 点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B.100°
C.40°或140° D.40°或100°
6. 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是( )
A.70° B.50° C.45° D.20°
7. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,∠B=20°,则∠C的度数为( )
A.70° B.60° C.50° D.40°
8. 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,到半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
A.3π B.4π C.5π D.6π
9.如图,AB为半圆O的直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连结OD,OC,下列结论:①∠DOC=90°;②AD+BC=CD;③S△AOD∶S△BOC=AD2∶AO2;④OD∶OC=DE∶EC;⑤OD2=DE·CD.正确的有( )
A.2个 B.3个 C.4个 D.5个
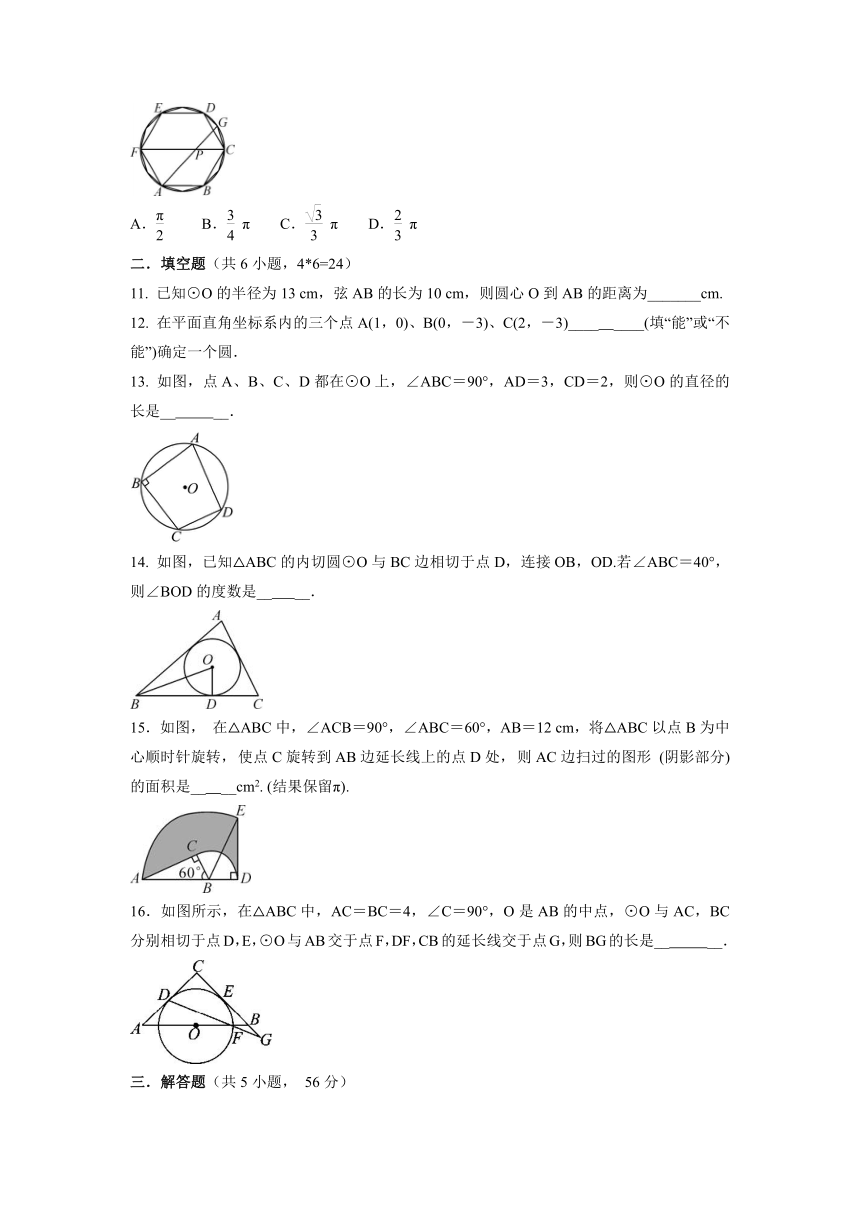
10. 如图,六边形ABCDEF是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结AG,CF,AG交CF于点P,若AP=2.则的长为( )
A. B.π C.π D.π
二.填空题(共6小题,4*6=24)
11. 已知⊙O的半径为13 cm,弦AB的长为10 cm,则圆心O到AB的距离为_______cm.
12. 在平面直角坐标系内的三个点A(1,0)、B(0,-3)、C(2,-3)____ ____(填“能”或“不能”)确定一个圆.
13. 如图,点A、B、C、D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是__ __.
14. 如图,已知△ABC的内切圆⊙O与BC边相切于点D,连接OB,OD.若∠ABC=40°,则∠BOD的度数是__ __.
15.如图, 在△ABC中,∠ACB=90°,∠ABC=60°,AB=12 cm,将△ABC以点B为中心顺时针旋转, 使点C旋转到AB边延长线上的点D处, 则AC边扫过的图形 (阴影部分) 的面积是__ __cm2. (结果保留π).
16.如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC,BC分别相切于点D,E,⊙O与AB交于点F,DF,CB的延长线交于点G,则BG的长是__ __.
三.解答题(共5小题, 56分)
17.(6分) 如图,AB是半圆O的直径,C,D是半圆O上的两点,OD∥BC,OD与AC交于点E.
(1)若∠D=70°,求∠CAD的度数;
(2)若AC=8,DE=2,求AB的长.
18.(8分) 如图,水平放置的圆柱形排水管的截面为⊙O,有水部分弓形的高为2,弦AB=4,求⊙O的半径.
19.(8分) 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC.
(2)若⊙O的半径为4,∠BAC=60°,求DE的长.
20.(10分) 如图,AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:△ACB∽△CDB;
(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积.
21.(12分) 如图,已知PA、PB分别切⊙O于点A、B,BC为⊙O的直径.
(1)求证:AC∥OP;
(2)若∠APB=60°,BC=10 cm,求AC的长.
22.(12分) 如图,已知⊙O上依次有A,B,C,D四个点, =,连接AB,AD,BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
(1)若⊙O的半径为3,∠DAB=120°,求劣弧的长;
(2)求证:BF=BD;
(3)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.
参考答案
1-5BABDC 6-10BCCCD
11.12
12.能
13.
17.70°
15.36π
16.2-2
17.解:(1)∵OA=OD,∠D=70°,∴∠OAD=∠D=70°,∴∠AOD=180°-∠OAD-∠D=40°.∵AB是半圆O的直径,∴∠C=90°.∵OD∥BC,∴∠AEO=∠C=90°,即OD⊥AC.∴=,∴∠CAD=∠AOD=20°.
(2)由(1)可知OD⊥AC,∴AE=AC=×8=4.设OA=x,则OE=OD-DE=x-2.在Rt△OAE中,OE2+AE2=OA2,即(x-2)2+42=x2,解得x=5.∴AB=2OA=10.
18.解:过点O作OC⊥AB于点C,连结OB,设⊙O的半径为r,则OC=r-2,∵OC⊥AB,∴BC=AB=×4=2.在Rt△BOC中,∵OC2+BC2=OB2,即(r-2)2+(2)2=r2,解得r=4.
19.(1)证明:如图,连接AD.∵AB是⊙O的直径,∴∠ADB=90°.∵DC=BD,∴AB=AC.
(2)解:由(1)知AB=AC,∵∠BAC=60°,∠ADB=90°,∴△ABC是等边三角形,∠BAD=30°.∴∠C=60°.在Rt△BAD中,∠BAD=30°,AB=8,∴BD=4,∴DC=4.∵DE⊥AC,∴∠DEC=90°,∴∠CDE=30°,∴CE=DC=2.∴DE==2.
20.解:(1)∵直线CP是⊙O的切线,∴∠BCD=∠BAC,∵AB是直径,∴∠ACB=90°,又∵BD⊥CP,∴∠CDB=90°,∴∠ACB=∠CDB=90°,∴△ACB∽△CDB
(2)连结OC,∵直线CP是⊙O的切线,∠BCP=30°,∴∠COB=2∠BCP=60°,∴△OCB是正三角形,∵⊙O的半径为1,∴S△OCB=,S扇形OCB==π,∴S阴影=S扇形OCB-S△OCB=-
21.解:(1)证明:连结OA. ∵PA、PB分别切⊙O于点A、B,∴OA⊥PA,OB⊥PB,PA=PB,∴OP平分∠AOB,∴∠BOA=2∠POB.∵∠OAC=∠C,∴∠BOA=∠C+∠OAC=2∠C,∴∠POB=∠C,∴AC∥OP.
(2)连结AB. ∵PA=PB,∠APB=60°,∴△PAB是等边三角形,∴∠PBA=60°.又∵∠PBC=90°,∴∠ABC=30°.∵BC为⊙O的直径,∴∠BAC=90°,∴AC=BC=5 cm.
22.解:(1)连接OB,OD,∵∠DAB=120°,∴所对圆心角的度数为240°,∴∠BOD=120°.∵⊙O的半径为3,∴劣弧的长为×π×3=2π
(2)连接AC,∵AB=BE,∴点B为AE的中点.∵F是EC的中点,∴BF为△EAC的中位线,∴BF=AC.∵=,∴+=+,∴=,∴BD=AC,∴BF=BD
(3)过点B作AE的垂线,与⊙O的交点即为所求的点P,∵BF为△EAC的中位线,∴BF∥AC,∴∠FBE=∠CAE.∵=,∴∠DBA=∠CAB,∴∠FBE=∠DBA.由作法可知BP⊥AE,∴∠GBP=∠FBP.∵G为BD的中点,∴BG=BD,∴BG=BF.在△PBG和△PBF中,BG=BF,∠PBG=∠PBF,BP=BP,∴△PBG≌△PBF(SAS),∴PG=PF.故在⊙O上存在点P,使得PG=PF,此时PB⊥AE
第27章 圆
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列说法正确的是( )
A.平分弦的直径垂直于弦
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.若直线与圆有公共点,则直线与圆相切
2. 在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以点O为圆心,OA的长为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的树为( )
A.E、F、G B.F、G、H
C.G、H、E D.H、E、F
3. 如图,AB是⊙O的直径,D、C在⊙O上,AD∥OC,∠DAC=30°,连结AC,则∠BOC的度数为( )
A.30° B.60° C.45° D.80°
4. 如图,在△ABC中,∠BAC=28°,以AB为直径的⊙O交AC于点D,DE∥CB,连结BD,若添加一个条件,使BC是⊙O的切线,则下列四个条件中不符合的是( )
A.DE⊥AB B.∠EDB=28°
C.∠ADE=∠ABD D.OB=BC
5. 点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B.100°
C.40°或140° D.40°或100°
6. 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是( )
A.70° B.50° C.45° D.20°
7. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,∠B=20°,则∠C的度数为( )
A.70° B.60° C.50° D.40°
8. 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,到半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
A.3π B.4π C.5π D.6π
9.如图,AB为半圆O的直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连结OD,OC,下列结论:①∠DOC=90°;②AD+BC=CD;③S△AOD∶S△BOC=AD2∶AO2;④OD∶OC=DE∶EC;⑤OD2=DE·CD.正确的有( )
A.2个 B.3个 C.4个 D.5个
10. 如图,六边形ABCDEF是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结AG,CF,AG交CF于点P,若AP=2.则的长为( )
A. B.π C.π D.π
二.填空题(共6小题,4*6=24)
11. 已知⊙O的半径为13 cm,弦AB的长为10 cm,则圆心O到AB的距离为_______cm.
12. 在平面直角坐标系内的三个点A(1,0)、B(0,-3)、C(2,-3)____ ____(填“能”或“不能”)确定一个圆.
13. 如图,点A、B、C、D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是__ __.
14. 如图,已知△ABC的内切圆⊙O与BC边相切于点D,连接OB,OD.若∠ABC=40°,则∠BOD的度数是__ __.
15.如图, 在△ABC中,∠ACB=90°,∠ABC=60°,AB=12 cm,将△ABC以点B为中心顺时针旋转, 使点C旋转到AB边延长线上的点D处, 则AC边扫过的图形 (阴影部分) 的面积是__ __cm2. (结果保留π).
16.如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC,BC分别相切于点D,E,⊙O与AB交于点F,DF,CB的延长线交于点G,则BG的长是__ __.
三.解答题(共5小题, 56分)
17.(6分) 如图,AB是半圆O的直径,C,D是半圆O上的两点,OD∥BC,OD与AC交于点E.
(1)若∠D=70°,求∠CAD的度数;
(2)若AC=8,DE=2,求AB的长.
18.(8分) 如图,水平放置的圆柱形排水管的截面为⊙O,有水部分弓形的高为2,弦AB=4,求⊙O的半径.
19.(8分) 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC.
(2)若⊙O的半径为4,∠BAC=60°,求DE的长.
20.(10分) 如图,AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:△ACB∽△CDB;
(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积.
21.(12分) 如图,已知PA、PB分别切⊙O于点A、B,BC为⊙O的直径.
(1)求证:AC∥OP;
(2)若∠APB=60°,BC=10 cm,求AC的长.
22.(12分) 如图,已知⊙O上依次有A,B,C,D四个点, =,连接AB,AD,BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
(1)若⊙O的半径为3,∠DAB=120°,求劣弧的长;
(2)求证:BF=BD;
(3)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.
参考答案
1-5BABDC 6-10BCCCD
11.12
12.能
13.
17.70°
15.36π
16.2-2
17.解:(1)∵OA=OD,∠D=70°,∴∠OAD=∠D=70°,∴∠AOD=180°-∠OAD-∠D=40°.∵AB是半圆O的直径,∴∠C=90°.∵OD∥BC,∴∠AEO=∠C=90°,即OD⊥AC.∴=,∴∠CAD=∠AOD=20°.
(2)由(1)可知OD⊥AC,∴AE=AC=×8=4.设OA=x,则OE=OD-DE=x-2.在Rt△OAE中,OE2+AE2=OA2,即(x-2)2+42=x2,解得x=5.∴AB=2OA=10.
18.解:过点O作OC⊥AB于点C,连结OB,设⊙O的半径为r,则OC=r-2,∵OC⊥AB,∴BC=AB=×4=2.在Rt△BOC中,∵OC2+BC2=OB2,即(r-2)2+(2)2=r2,解得r=4.
19.(1)证明:如图,连接AD.∵AB是⊙O的直径,∴∠ADB=90°.∵DC=BD,∴AB=AC.
(2)解:由(1)知AB=AC,∵∠BAC=60°,∠ADB=90°,∴△ABC是等边三角形,∠BAD=30°.∴∠C=60°.在Rt△BAD中,∠BAD=30°,AB=8,∴BD=4,∴DC=4.∵DE⊥AC,∴∠DEC=90°,∴∠CDE=30°,∴CE=DC=2.∴DE==2.
20.解:(1)∵直线CP是⊙O的切线,∴∠BCD=∠BAC,∵AB是直径,∴∠ACB=90°,又∵BD⊥CP,∴∠CDB=90°,∴∠ACB=∠CDB=90°,∴△ACB∽△CDB
(2)连结OC,∵直线CP是⊙O的切线,∠BCP=30°,∴∠COB=2∠BCP=60°,∴△OCB是正三角形,∵⊙O的半径为1,∴S△OCB=,S扇形OCB==π,∴S阴影=S扇形OCB-S△OCB=-
21.解:(1)证明:连结OA. ∵PA、PB分别切⊙O于点A、B,∴OA⊥PA,OB⊥PB,PA=PB,∴OP平分∠AOB,∴∠BOA=2∠POB.∵∠OAC=∠C,∴∠BOA=∠C+∠OAC=2∠C,∴∠POB=∠C,∴AC∥OP.
(2)连结AB. ∵PA=PB,∠APB=60°,∴△PAB是等边三角形,∴∠PBA=60°.又∵∠PBC=90°,∴∠ABC=30°.∵BC为⊙O的直径,∴∠BAC=90°,∴AC=BC=5 cm.
22.解:(1)连接OB,OD,∵∠DAB=120°,∴所对圆心角的度数为240°,∴∠BOD=120°.∵⊙O的半径为3,∴劣弧的长为×π×3=2π
(2)连接AC,∵AB=BE,∴点B为AE的中点.∵F是EC的中点,∴BF为△EAC的中位线,∴BF=AC.∵=,∴+=+,∴=,∴BD=AC,∴BF=BD
(3)过点B作AE的垂线,与⊙O的交点即为所求的点P,∵BF为△EAC的中位线,∴BF∥AC,∴∠FBE=∠CAE.∵=,∴∠DBA=∠CAB,∴∠FBE=∠DBA.由作法可知BP⊥AE,∴∠GBP=∠FBP.∵G为BD的中点,∴BG=BD,∴BG=BF.在△PBG和△PBF中,BG=BF,∠PBG=∠PBF,BP=BP,∴△PBG≌△PBF(SAS),∴PG=PF.故在⊙O上存在点P,使得PG=PF,此时PB⊥AE
