华东师大版七年级下册数学 9.2 多边形的内角和 教案
文档属性
| 名称 | 华东师大版七年级下册数学 9.2 多边形的内角和 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 92.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 00:00:00 | ||
图片预览

文档简介
多边形的内角和
华东师大2011版 七年级下
教学目标
1.使学生了解多边形及多边形的内角、外角等概念。
2.使学生通过不同方法探索多边形的内角和公式,并会利用它进行有关计算。
重点、难点
1.重点:多边形的内角和定理。
2.难点:多边形的内角和定理的推导。
教学过程
一、复习提问
1.什么叫三角形
2.三角形的内角和是多少
3.什么叫三角形的外角 什么叫外角和 三角形的外角和是多少
二、新知讲解
1.多边形的概念,
三角形有三个内角、三条边,我们也可以把三角形称为三边形(但习惯称三角形)。我们知道:不在同一直线上的三条线段首尾顺次连结组成的平面图形叫三角形。
你能说出什么叫四边形、五边形吗
一般地,由n条不在同一直线上的线段首尾顺次连结组成的平面图形,记为n边形,又称多边形。
如果多边形的各边都相等,各内角也都相等,则称为正多边形,如正三角形、正四边形(正方形)、正五边形等等。连结多边形不相邻的两个顶点的线段叫做多边形的对角线,如图1,线段AC是四边形 ABCD的对角线,如图2,线段AD、AC是四边形ABCDE的对角线,如图3中线段AC、AD、AE是六边形ABCDEF的对角线。
问: (1)四边形有几条对角线 (两条AC、BD)
(2)五边形有几条对角线
(3)六边形有几条对角线 n边形呢
从以上分析可知从n边形的一个顶点引对角线,可以引(n-3)条, (除本身这个点以及和这点相邻的两点外),那么n个顶点,就有n(n- 3)条。
2.多边形的内角和公式。
三角形是边数最少的多边形,它的内角和等于180°,那么一般n边形是否也有内角和公式呢 让我们先从四边形,正边形,六边形……开始。
从上面对角线的研究可知,一条对角线把四边形分成2个三角形,这两个三角形的内角和的和就是四边形的内角和,五边形的内角和就是图中3个三角表内角和的和。
让学生填写表,由此,你可以得到”边形的内角和公式吗
n边形的内角和=(n-2)·180°
知道一个多边形的内角和,根据公式也可以求边数n。
知道多边形的边数,可以求出多边形的度数
例1.求八边形的内角和的度数。
分析: n边形的内角和公式为(n-2) 180 ° ,现在知道这个多边形的边数是八,代入这个公式既可求出.
解 : (n-2)×180°
=(8-2)×180°
=1 080°
例2.略
多边形的内角和等于(n-2)·180°,还可以用以下的划分来说明,即在n边形内任取一点P,连结点P与多边形的每个顶点,可得几个三角形 这几个三角形的各内角与这个多边的各内角之间有什么关系 请你试一试。
问:还有其他方法吗 让学生自主探索,对不同方法给予鼓励。
三、巩固练习
1.略
2.多边形的内角和为1620°,则它为_____边行。多边形每个内角都等于120°,则它为_____边形。
3.四边形各内角的度数之比为2∶3∶5∶8,则各角度数为 .
四、小结
本节课我们通过把多边形划分成若干个三角形,用三角形内角和去求多边形的内角和,从而得到多边形的内角和公式为(n-2)·180°。这种化未知为已知的转化方法,必须在学习中逐步掌握。希望同学们在以后学习生活中勤思考,多练习!灵活运用所学知识解题。
五、作业
教科书P88习题9.2第1、2、3、题。
教科书第88页练习1、2。
。
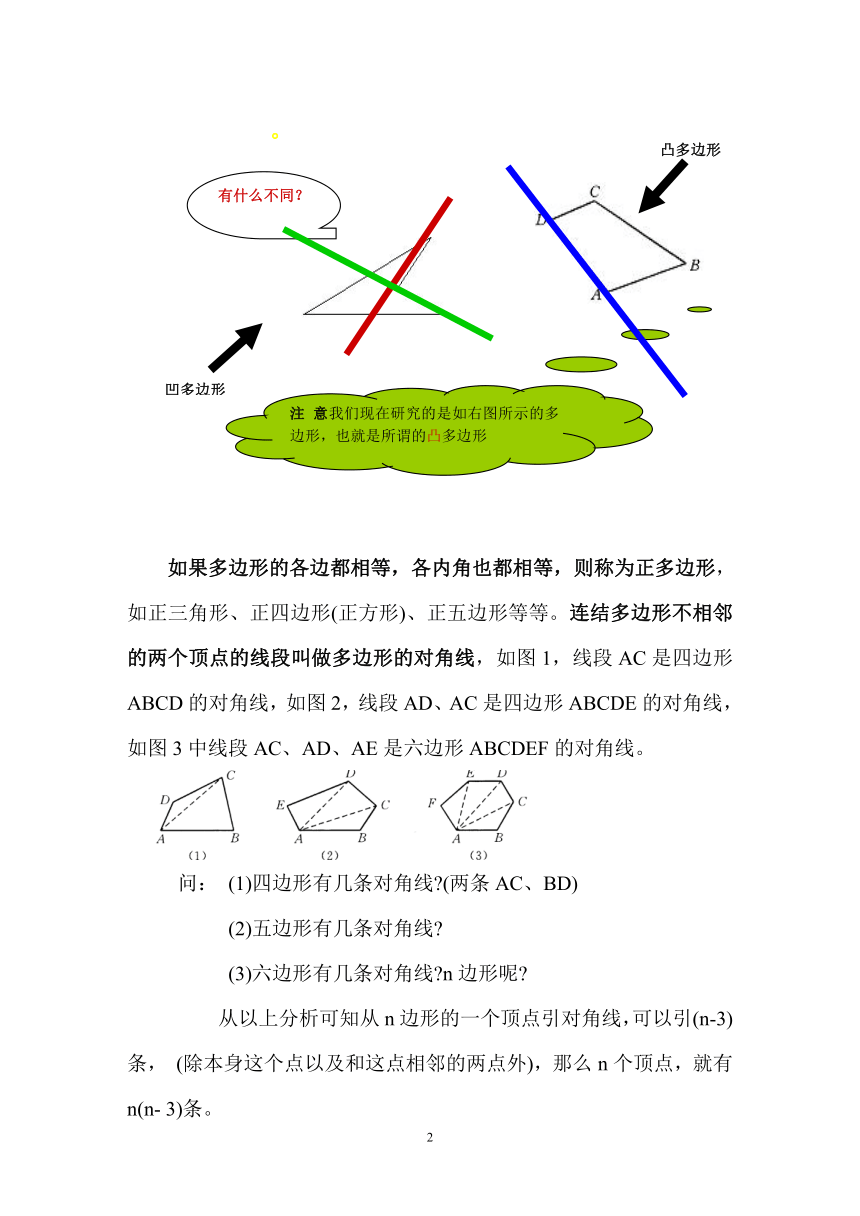
注 意我们现在研究的是如右图所示的多边形,也就是所谓的凸多边形
有什么不同?
凹多边形
凸多边形
PAGE
4
华东师大2011版 七年级下
教学目标
1.使学生了解多边形及多边形的内角、外角等概念。
2.使学生通过不同方法探索多边形的内角和公式,并会利用它进行有关计算。
重点、难点
1.重点:多边形的内角和定理。
2.难点:多边形的内角和定理的推导。
教学过程
一、复习提问
1.什么叫三角形
2.三角形的内角和是多少
3.什么叫三角形的外角 什么叫外角和 三角形的外角和是多少
二、新知讲解
1.多边形的概念,
三角形有三个内角、三条边,我们也可以把三角形称为三边形(但习惯称三角形)。我们知道:不在同一直线上的三条线段首尾顺次连结组成的平面图形叫三角形。
你能说出什么叫四边形、五边形吗
一般地,由n条不在同一直线上的线段首尾顺次连结组成的平面图形,记为n边形,又称多边形。
如果多边形的各边都相等,各内角也都相等,则称为正多边形,如正三角形、正四边形(正方形)、正五边形等等。连结多边形不相邻的两个顶点的线段叫做多边形的对角线,如图1,线段AC是四边形 ABCD的对角线,如图2,线段AD、AC是四边形ABCDE的对角线,如图3中线段AC、AD、AE是六边形ABCDEF的对角线。
问: (1)四边形有几条对角线 (两条AC、BD)
(2)五边形有几条对角线
(3)六边形有几条对角线 n边形呢
从以上分析可知从n边形的一个顶点引对角线,可以引(n-3)条, (除本身这个点以及和这点相邻的两点外),那么n个顶点,就有n(n- 3)条。
2.多边形的内角和公式。
三角形是边数最少的多边形,它的内角和等于180°,那么一般n边形是否也有内角和公式呢 让我们先从四边形,正边形,六边形……开始。
从上面对角线的研究可知,一条对角线把四边形分成2个三角形,这两个三角形的内角和的和就是四边形的内角和,五边形的内角和就是图中3个三角表内角和的和。
让学生填写表,由此,你可以得到”边形的内角和公式吗
n边形的内角和=(n-2)·180°
知道一个多边形的内角和,根据公式也可以求边数n。
知道多边形的边数,可以求出多边形的度数
例1.求八边形的内角和的度数。
分析: n边形的内角和公式为(n-2) 180 ° ,现在知道这个多边形的边数是八,代入这个公式既可求出.
解 : (n-2)×180°
=(8-2)×180°
=1 080°
例2.略
多边形的内角和等于(n-2)·180°,还可以用以下的划分来说明,即在n边形内任取一点P,连结点P与多边形的每个顶点,可得几个三角形 这几个三角形的各内角与这个多边的各内角之间有什么关系 请你试一试。
问:还有其他方法吗 让学生自主探索,对不同方法给予鼓励。
三、巩固练习
1.略
2.多边形的内角和为1620°,则它为_____边行。多边形每个内角都等于120°,则它为_____边形。
3.四边形各内角的度数之比为2∶3∶5∶8,则各角度数为 .
四、小结
本节课我们通过把多边形划分成若干个三角形,用三角形内角和去求多边形的内角和,从而得到多边形的内角和公式为(n-2)·180°。这种化未知为已知的转化方法,必须在学习中逐步掌握。希望同学们在以后学习生活中勤思考,多练习!灵活运用所学知识解题。
五、作业
教科书P88习题9.2第1、2、3、题。
教科书第88页练习1、2。
。
注 意我们现在研究的是如右图所示的多边形,也就是所谓的凸多边形
有什么不同?
凹多边形
凸多边形
PAGE
4
