华东师大版七年级下册数学 10.5 图形的全等 课件(共21张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 10.5 图形的全等 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
10.5 图形的全等
情境引入
在通往数学王国的道路上,有一天,小聪聪遇到了一个难题:在一个房间内有四扇门,其中只有一扇是智慧之门,小聪聪只知道这扇门与其他几扇门不太一样,有它自己特有的特征。但是,特征是什么,他也不知道,只能通过自己的观察来作出判断。同学们,假如你是小聪聪,你会选择哪一扇门呢
请欣赏图片
能够完全重合的两个图形称为全等图形。
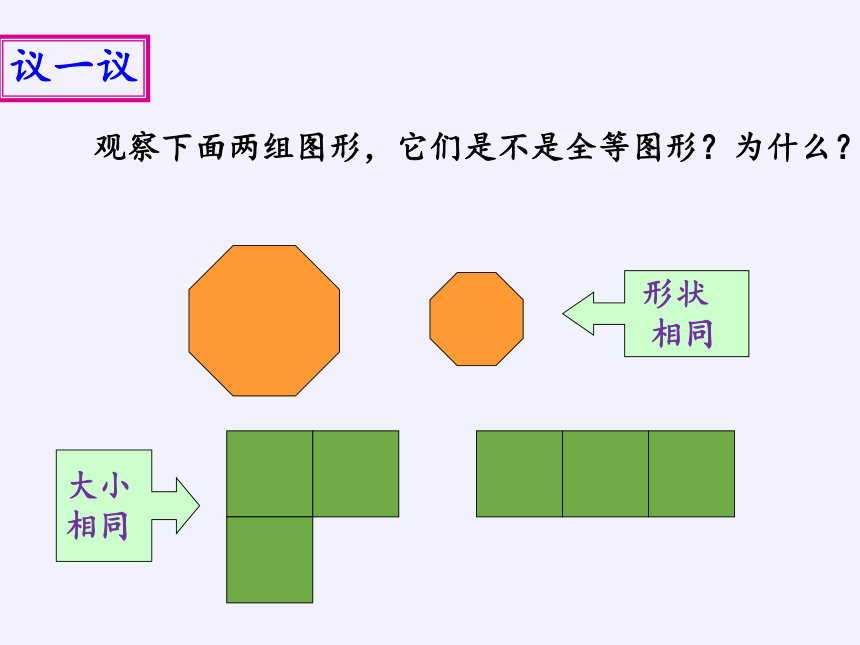
大小
相同
议一议
观察下面两组图形,它们是不是全等图形?为什么?
形状
相同
观察下列各组图形是不是全等图形 为什么
全等图形的 和 都相同。
形状
大小
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
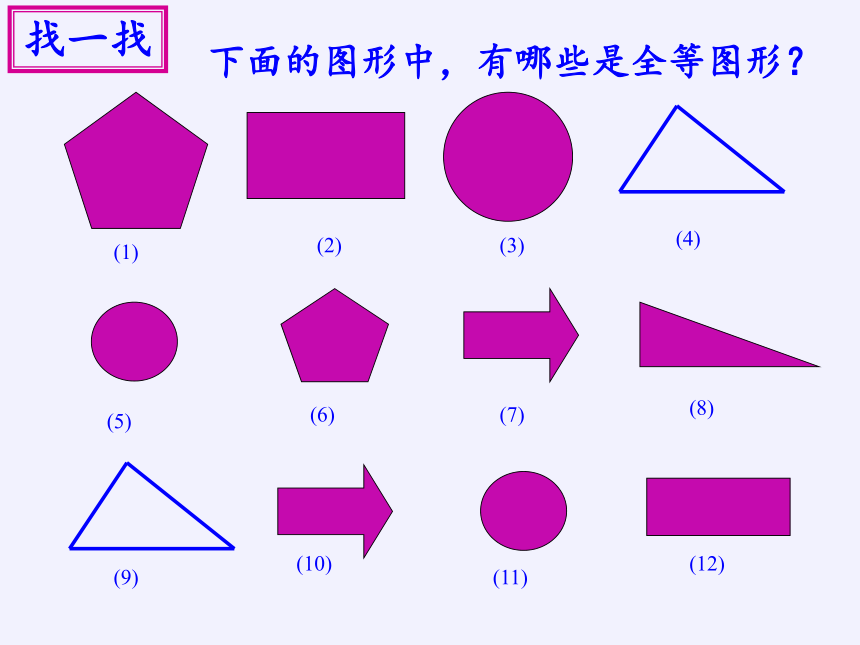
下面的图形中,有哪些是全等图形?
找一找
说一说
说说你生活中见过的全等图形的例子。
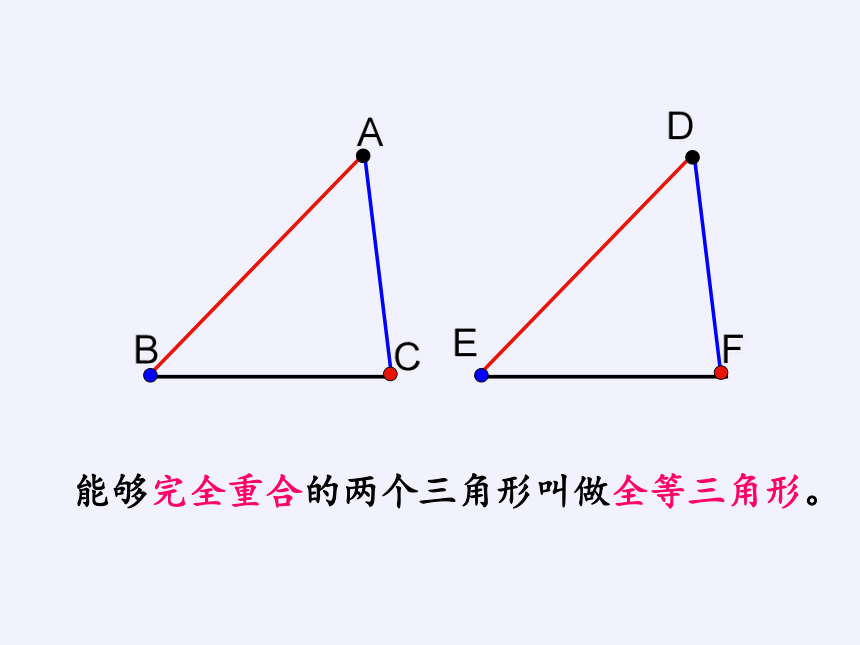
能够完全重合的两个三角形叫做全等三角形。
A
B
C
D
E
F
表示方法:如图,图中的两个三角形是全等的
注意:对应顶点的字母应该写在对应的位置上。
A
B
C
E
D
F
记作:△ABC≌△DEF
读作:△ABC全等于△DEF
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
全等三角形的性质
全等三角形的对应边相等,对应角相等。
D
E
F
A
B
C
∵△ABC≌△DEF
∴AB=DE AC=DF BC=EF (全等三角形的对应边相等)
∠A=∠D ∠B=∠E ∠C=∠F
(全等三角形的对应角相等)
A
D
B
C
E
F
≌
试一试: 根据图形所提供的条件和全等式:
(1)在图上标出所缺的字母;
(2)说出它们的对应边和对应角
对应边:AF ED,AB EC,FB DC
对应角:∠A ∠E, ∠F ∠D, ∠B ∠C
= = =
与 与 与
与 与 与
= = =
已知,△ABC≌△DEF,AM是△ABC的高,DN是△DEF的高,AM与DN相等吗?
A
B
C
M
E
D
F
N
全等三角形的对应线段都相等
议一议
练一练
1、如图:△ABC≌△AEC,∠B=30°,∠ACB=85°,求出△AEC各内角的度数。
解:∵ △AEC≌△ABC
∴ ∠E=∠B=30°
∠ACE=∠ACB=85°
∠EAC=∠BAC
=180°-30°-85°
=65°
2、如图:△ABD≌ △EBC,AB=3cm,BC=5cm, 求DE的长。
解:∵△ABD≌ △EBC
∴AB=EB、BD=BC
∵BD=DE+EB
∴DE=BD-EB
=BC-AB
=5-3=2cm
下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?
延伸与拓展
全等图形
对应边
对应角
对应顶点
能够重合的两个三角形
互相重合的角叫做__ _.
互相重合的边叫做____;
其中:互相重合的顶点叫做_ _ _;
4.书写全等式时要求把对应字母写在对应的位置上
2. 叫做全等三角形。
1.能够重合的两个图形叫做 。
5.全等三角形的 和 分别相等
3.“全等”用符号“≌”来表示,读作“ ”
对应边
对应角
全等于
谈谈你的收获
必做题:习题4.5 第2、3题
作 业
选做题:如图,如果△ADE ≌ △CBF,那么AE∥CF吗? 说明理由。
A
C
D
B
E
F
图片欣赏
谢 谢
10.5 图形的全等
情境引入
在通往数学王国的道路上,有一天,小聪聪遇到了一个难题:在一个房间内有四扇门,其中只有一扇是智慧之门,小聪聪只知道这扇门与其他几扇门不太一样,有它自己特有的特征。但是,特征是什么,他也不知道,只能通过自己的观察来作出判断。同学们,假如你是小聪聪,你会选择哪一扇门呢
请欣赏图片
能够完全重合的两个图形称为全等图形。
大小
相同
议一议
观察下面两组图形,它们是不是全等图形?为什么?
形状
相同
观察下列各组图形是不是全等图形 为什么
全等图形的 和 都相同。
形状
大小
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
下面的图形中,有哪些是全等图形?
找一找
说一说
说说你生活中见过的全等图形的例子。
能够完全重合的两个三角形叫做全等三角形。
A
B
C
D
E
F
表示方法:如图,图中的两个三角形是全等的
注意:对应顶点的字母应该写在对应的位置上。
A
B
C
E
D
F
记作:△ABC≌△DEF
读作:△ABC全等于△DEF
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
全等三角形的性质
全等三角形的对应边相等,对应角相等。
D
E
F
A
B
C
∵△ABC≌△DEF
∴AB=DE AC=DF BC=EF (全等三角形的对应边相等)
∠A=∠D ∠B=∠E ∠C=∠F
(全等三角形的对应角相等)
A
D
B
C
E
F
≌
试一试: 根据图形所提供的条件和全等式:
(1)在图上标出所缺的字母;
(2)说出它们的对应边和对应角
对应边:AF ED,AB EC,FB DC
对应角:∠A ∠E, ∠F ∠D, ∠B ∠C
= = =
与 与 与
与 与 与
= = =
已知,△ABC≌△DEF,AM是△ABC的高,DN是△DEF的高,AM与DN相等吗?
A
B
C
M
E
D
F
N
全等三角形的对应线段都相等
议一议
练一练
1、如图:△ABC≌△AEC,∠B=30°,∠ACB=85°,求出△AEC各内角的度数。
解:∵ △AEC≌△ABC
∴ ∠E=∠B=30°
∠ACE=∠ACB=85°
∠EAC=∠BAC
=180°-30°-85°
=65°
2、如图:△ABD≌ △EBC,AB=3cm,BC=5cm, 求DE的长。
解:∵△ABD≌ △EBC
∴AB=EB、BD=BC
∵BD=DE+EB
∴DE=BD-EB
=BC-AB
=5-3=2cm
下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?
延伸与拓展
全等图形
对应边
对应角
对应顶点
能够重合的两个三角形
互相重合的角叫做__ _.
互相重合的边叫做____;
其中:互相重合的顶点叫做_ _ _;
4.书写全等式时要求把对应字母写在对应的位置上
2. 叫做全等三角形。
1.能够重合的两个图形叫做 。
5.全等三角形的 和 分别相等
3.“全等”用符号“≌”来表示,读作“ ”
对应边
对应角
全等于
谈谈你的收获
必做题:习题4.5 第2、3题
作 业
选做题:如图,如果△ADE ≌ △CBF,那么AE∥CF吗? 说明理由。
A
C
D
B
E
F
图片欣赏
谢 谢
