7.2 万有引力定律计算题练习(word版含答案)
文档属性
| 名称 | 7.2 万有引力定律计算题练习(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 854.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-16 00:00:00 | ||
图片预览




文档简介
万有引力定律计算题练习
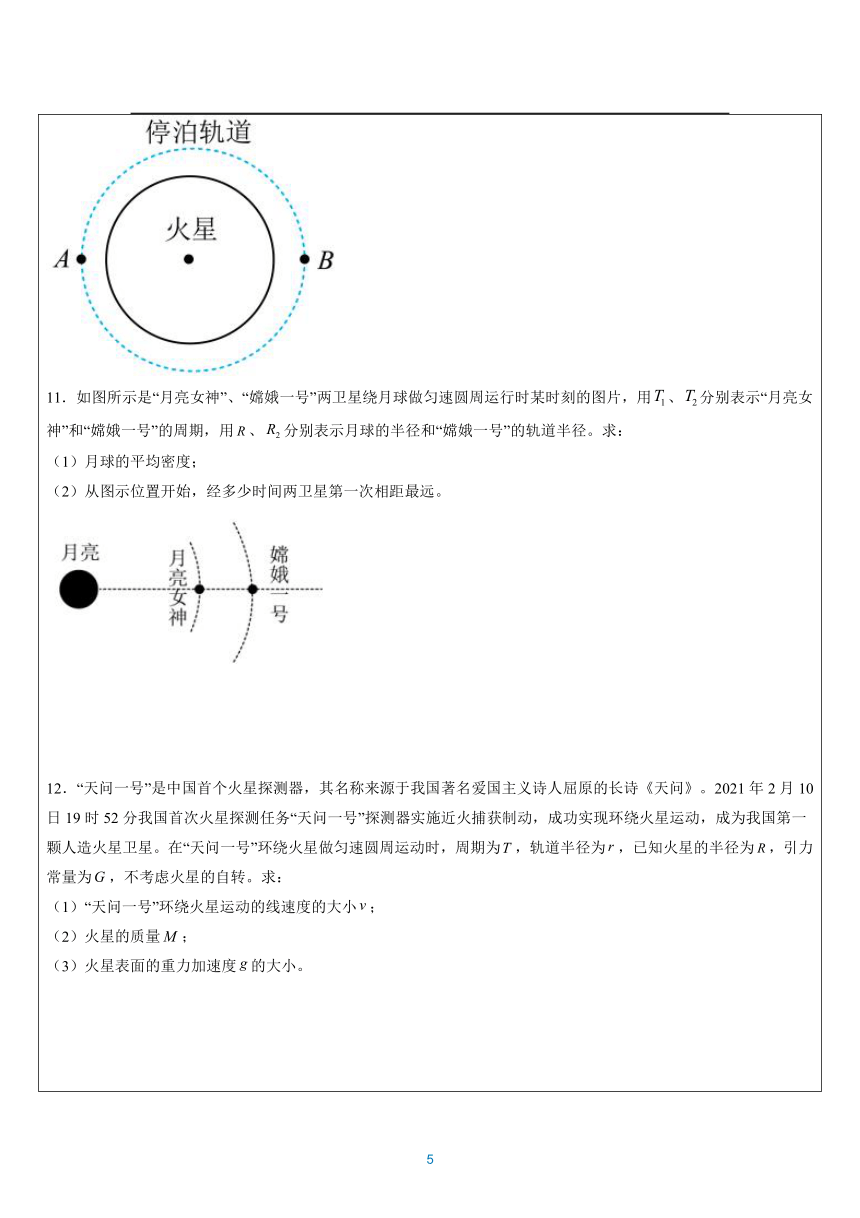
1.航天员景海鹏和陈冬进入天宫二号,开展相关空间科学试验。航天员测出天宫二号绕地球做匀速圆周运动的周期为T,距地面的高度为h,已知地球半径为R,引力常量为G,不考虑地球的自转。求: (1)地球的平均密度; (2)地球表面的重力加速度。 2.2019年1月3日,我国“嫦娥四号”探测器成功着陆在月球背面预选着陆区,月球车“玉兔二号”到达月面开始巡视探测,对研究月球和太阳系早期历史具有重要价值。已知地球半径为R,地球表面的重力加速度大小为g,月球半径是地球的,质量是地球的,着陆前探测器在距月面高度为h的环月轨道上做圆周运动。求: (1)月球表面处重力加速度的大小; (2)探测器在环月轨道上做圆周运动的周期T。 3.宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处。(取地球表面重力加速度g1=10m/s2,空气阻力不计, 该星球的半径与地球半径之比为R星∶R地=1∶4) 求: (1) 求该星球表面附近的重力加速度g2; (2) 求该星球的质量与地球质量之比M星∶M地。 4.2021年10月16日,我国成功发射了神舟十三号载人飞船,与空间站组合体完成自主快速交会对接,3名航天员翟志刚、王亚平、叶光富成功送入了天和核心舱,他们将在轨驻留6个月,任务主要目标为验证中国空间站建造相关技术,为我国空间站后续建造及运营任务奠定基础。 已知神舟十三号与空间站组合体完成对接后在轨道上运行,可视为匀速圆周运动,它们飞行n圈所用时间为t。已知它们的总质量为m,它们距地面的高度为h,地球半径为R,引力常量为G。求: (1)神舟十三号与空间站组合体对接后,地球对它们的万有引力F; (2)地球的质量M; (3)地球表面的重力加速度g。 5.祝融号火星车在着陆火星之前,需经历动力减速、悬停避障两个阶段。在动力减速阶段可视为匀减速运动,速度大小由96m/s减小到0,历时80s。在悬停避障阶段,火星车将启用最大推力为7500N的变推力发动机,在距火星表面约百米高度处悬停,寻找着陆点。已知火星半径约为地球半径的,火星质量约为地球质量的,地球表面重力加速度大小取10m/s2,求: (1)在动力减速阶段的加速度大小和下降距离; (2)在悬停避障阶段,火星车能借助该变推力发动机实现悬停,若已知火星车质量为240kg,求火星车能携带物资的最大质量。 6.遥远的星球。某星球完全由不可压缩的液态水组成。星球的表面重力加速度为,半径为R,且没有自转。水的密度,万有引力常数。本题中可能用到如下公式:半径为R的球,其体积为,表面积为。 (1)星球的半径R是多少? (2)星球内部的重力加速度为,其中r是到球心的距离。请通过分析画出图。(提示:已知均匀球壳对球壳内部物体的万有引力为零) (3)假定该星球没有大气层,求这个星球中心处由水产生的压强。 7.“嫦娥一号”卫星在距月球表面高度为h处做匀速圆周运动的周期为T,已知月球半径为R,引力常量为G,(球的体积公式,其中R为球的半径)求: (1)月球的质量M; (2)月球表面的重力加速度g月; (3)月球的密度ρ。 8.宇航员在某质量分布均匀的星球表面,以速度v0竖直上抛一质量为m的物体(引力视为恒力,阻力可忽略),经过时间t落到地面。已知该行星半径为R,引力常量为G,忽略星球自转的影响,求: (1)该星球表面的重力加速度大小; (2)该星球的质量; (3)该星球的密度。 9.一个到达月球的宇航员随身携带一质量为1.0kg的物体A,在月球某处他捡起一块岩石B,然后他把A和B用轻绳连接并挂在一个定滑轮上(不计滑轮与绳的摩擦),如图所示,测量得到B下落的加速度为1.2m/s2.已知地球质量约为月球质量的81倍,地球半径约为月球半径倍,地球表面重力加速度约为10m/s2,计算结果均保留两位有效数字。求: (1)月球表面重力加速度约为多少 (2)B的质量约为多少 10.2021年2月,执行我国火星探测任务的“天问一号”探测器在成功实施三次近火制动后,进入近火点为A远火点为B的椭圆轨道上运行,A点距火星表面的高度为、B点距火星表面的高度为,探测器在椭圆轨道上运行的周期为。之后,探测器再经多次变轨,进入环绕火星表面的圆轨道上运行考察。最后,搭载“祝融号”火星车的着陆巡视器成功着陆火星表面。已知火星半径为R,引力常量为G。 (1)求探测器在环火表面圆轨道上运行的周期。 (2)火星着陆巡视器着陆火星的最后阶段,先在高度为h处悬停,关闭发动机后自由下落到火星表面,求其着陆时的速度。 11.如图所示是“月亮女神”、“嫦娥一号”两卫星绕月球做匀速圆周运行时某时刻的图片,用、分别表示“月亮女神”和“嫦娥一号”的周期,用、分别表示月球的半径和“嫦娥一号”的轨道半径。求: (1)月球的平均密度; (2)从图示位置开始,经多少时间两卫星第一次相距最远。 12.“天问一号”是中国首个火星探测器,其名称来源于我国著名爱国主义诗人屈原的长诗《天问》。2021年2月10日19时52分我国首次火星探测任务“天问一号”探测器实施近火捕获制动,成功实现环绕火星运动,成为我国第一颗人造火星卫星。在“天问一号”环绕火星做匀速圆周运动时,周期为,轨道半径为,已知火星的半径为,引力常量为,不考虑火星的自转。求: (1)“天问一号”环绕火星运动的线速度的大小; (2)火星的质量; (3)火星表面的重力加速度的大小。 13.2021年6月11日,天问一号探测器着陆火星首批科学影像图公布。质量为的天问一号在火星表面着陆前的动力减速阶段可看作竖直方向的匀变速直线运动,探测器发动机打开,会在火星表面附近经历一个时长为、速度由减速到零的过程。已知火星半径约为地球半径的二分之一,火星质量约为地球质量的八分之一,地球表面的重力加速度大小为,忽略火星大气阻力。求: (1)火星表面的重力加速度大小; (2)动力减速阶段着陆器受到的制动力大小。 14.我国发射的“嫦娥一号”探月卫星沿近似于圆形的轨道绕月飞行。设卫星距月球表面的高度为h,做匀速圆周运动的周期为T。已知月球半径为R,引力常量为G,球的体积公式。求: (1)月球的质量M; (2)月球表面的重力加速度g月; (3)月球的密度ρ。 15.开普勒第三定律指出:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等,该定律对一切具有中心天体的引力系统都成立。如图所示,已知嫦娥三号探月卫星在半径为r的圆形轨道Ⅰ上绕月球运行,周期为T,月球的半径为R,引力常量为G。某时刻嫦娥三号卫星在A点变轨进入椭圆轨道Ⅱ,在月球表面的B点着陆。A、O、B三点在一条直线上。求: (1)月球的密度; (2)探月卫星在轨道Ⅱ上从A点运动到B点所用的时间。 16.假设宇航员在质量为M,半径为R的某星球表面做了一个实验:将一个质量为m的物体置于半径为r的水平圆盘边缘,物体与圆盘间的动摩擦因数为μ,使圆盘绕过圆心的竖直轴转动,转速缓慢增加,某时刻物体从圆盘上滑出,经时间t落地。设引力常量为G;物体与圆盘间的最大静摩擦力等于滑动摩擦力。 求:(1)该星球表面的重力加速度大小; (2)物体离开圆盘时的速度大小; (3)落地点到圆盘圆心的水平距离。 17.2020年12月6日5时42分,嫦娥五号上升器成功与轨道器返回器组合体交会对接,并于6时12分将月球样品容器安全转移至返回器中。如图所示,返回式月球软着陆器在完成了对月球表面的考察任务后,由月球表面回到绕月球做圆周运动的轨道舱。已知月球表面的重力加速度为g,月球的半径为R,轨道舱到月球中心的距离为r,引力常量为G,不考虑月球的自转。求: (1)月球的质量M; (2)轨道舱绕月飞行的周期T。 18.2021年5月29日晚8时55分,中国“天舟二号”货运飞船从文昌航天发射场升空,飞船顺利进入预定轨道。5月30日上午5时01分,天舟二号货运飞船与天和核心舱交会对接,对接过程示意图如图所示。已知对接后的组合体沿圆形轨道运行,经过时间t,组合体绕地球球心转过的角度为,地球半径为R,地球表面重力加速度为g,引力常量为G,不考虑地球自转。求: (1)地球质量M; (2)组合体所在圆轨道距地面的高度H。 19.2021年5月15日,“天问一号”着陆巡视器成功着陆于火星乌托邦平原南部预选着陆区,我国首次火星探测任务着陆火星取得圆满成功。“天问一号”着陆巡视器质量为,其在火星表面着陆前的动力减速阶段可视为在竖直方向做匀变速直线运动,探测器制动打开后,会在火星表面附近经历一个时长为、速度由减速到零的过程。已知火星半径约为地球半径的二分之一,火星质量约为地球质量的十分之一,地球表面的重力加速度为,忽略火星大气阻力。求: (1)火星表面的重力加速度大小; (2)着陆巡视器在火星表面着陆前的动力减速阶段受到的制动力大小。 20.我国首次火星探测任务天问一号探测器在火星乌托邦平原南部预选着陆区着陆,迈出了我国星际探测征程的重要一步。探测器着陆前绕火星做匀速圆周运动,距火星表面的高度为h,做匀速圆周运动的角速度为ω,已知火星的半径为R,引力常量为G,(题中的字母是已知量),求: (1)火星的质量M的表达式; (2)火星表面的重力加速度g的表达式。 参考答案 1.(1);(2) 【解析】 (1)设地球质量为M,飞船质量为m 对飞船 联立得 (2)对地表上物体 联立得 2.(1);(2) 【解析】 (1)对于地球和月球表面的物体m,其重力近似等于万有引力,设地球质量为M,月球质量和半径分别为、,则 又 , 解得 (2)设探测器的质量为,其受到的万有引力提供向心力,则 又 ,, 解得 3.(1);(2) 【解析】 (1)竖直上抛运动的总时间 因为初速度相同,时间之比为1:5,所以星球表面的重力加速度 (2)设星球表面有一物体质量为m,则 所以 即 4.(1);(2);(3) 【解析】 (1)组合体绕地球运动的周期 则所受的万有引力为 (2) 根据万有引力等于向心力 解得地球的质量 (3)根据 解得 5.(1)1.2m/s2,3840m;(2)1635kg 【解析】 (1)在动力减速阶段所用时间为t,初速度大小为v1,末速度大小为v2,加速度大小为a,由匀变速直线运动速度公式有 代入题给数据得 设探测器下降的距离为s,由匀变速直线运动位移公式有 代入数据联立解得 (2)设火星的质量、半径和表面重力加速度大小分别为M火、r火和g火,地球的质量、半径和表面重力加速度大小分别为M地、r地和g地由牛顿运动定律和万有引力定律,对质量为m的物体有 式中G为引力常量。设变推力发动机的最大推力为F,能够悬停的火星车加物资最大质量为,由力的平衡条件有 代入数据联立解得 在悬停阶段,该变推力发动机能实现悬停携带物资最大质量约为 6.(1);(2) ;(3) 【解析】 (1)星球表面,万有引力等于重力 星球的质量 又 代入数据联立解得 (2)星球内部距球心处的重力加速度 则其图像为 (3)星球内部任意半径r处的重力加速度 现在做一根从星体表面到球心的细长的圆柱体液柱,圆柱体截面积是s,s非常小,星球中心的压力就是这个液柱的重力。因为液柱两侧的其他液体给予的力是垂直侧面的,没有径向分量,处液体体积元 则所受重力为 从球心处到星球表面重力积分为 则压强为 代入数据得 7.(1);(2);(3) 【解析】 (1)设“嫦娥一号”质量为m,根据牛顿第二定律有 ① 解得 ② (2)月球表面质量为m0的物体所受重力等于万有引力,即 ③ 联立②③解得 ④ (3)根据密度公式可得 ⑤ 8.(1);(2);(4) 【解析】 (1)设行星表面的重力加速度为,对小球,有 解得 (2)对行星表面的物体,有 故行星质量 (3)故行星的密度 可得 9.(1)1.7m/s2;(2)5.8kg 【解析】 (1)由 得 代入数据,可得 (2)对A、B利用牛顿第二定律得 解得 mB=5.8kg 10.(1);(2) 【解析】 (1)根据开普勒第三定律 解得 (2)在火星表面绕火星做圆周运动时 根据自由落体运动规律 解得 11.(1) ;(2) 【解析】 (1)设月球的质量为, 嫦娥一号的质量为,有 又 联立解得 (2)设经过时间两卫星第一次相距最远,有 解得 12.(1);(2);(3) 【解析】 (1)由线速度定义可得 (2)设“天问一号”的质量为m,引力提供向心力有 得 (3)忽略火星自转,火星表面质量为的物体,其所受引力等于重力 得 13.(1);(2) 【解析】 (1)由 解得火星表面的重力加速度与地球表面重力加速度的比值 即火星表面的重力加速度 (2)着陆器着陆过程可视为竖直向下的匀减速直线运动,由 可得 由牛顿第二定律有 解得此过程中着陆器受到的制动力大小 14.(1) ;(2) ;(3) 【解析】 (1)对卫星,由万有引力提供向心力,则 得 (2)假设月球表面附近有一物体m1,其所受万有引力等于其重力,则 解得 (3)根据 求得 15.(1);(2) 【解析】 (1)由万有引力充当向心力有 解得 月球的密度 解得 (2)椭圆轨道的半长轴 设椭圆轨道上运行周期为,由开普勒第三定律有 在轨道Ⅱ上运行的时间为 解得 16.(1);(2);(3) 【解析】 (1)由 得 (2)由 得 (3)水平射程 落地点到圆心的水平距离 17.(1);(2) 【解析】 (1)设月球表面上质量为m1的物体,其在月球表面有 月球质量 (2)轨道舱绕月球做圆周运动,设轨道舱的质量为m,由牛顿运动定律得 解得 18.(1);(2) 【解析】 (1)地球表面的万有引力等于重力 解得 (2)组合体运行的角速度 万有引力提供向心力 解得 19.(1);(2) 【解析】 (1)由 解得火星表面的重力加速度与地球表面重力加速度的比值 即火星表面的重力加速度 (2)着陆巡视器着陆过程可视为竖直向下的匀减速直线运动 由 可得 由牛顿第二定律有 解得此过程中着陆巡视器受到的制动力大小 20.(1);(2) 【解析】 (1)设探测器的质量为m,由万有引力提供向心力有 解得火星的质量 (2)设火星表面的物体质量为m1,物体受到的万有引力近似等于重力 联立解得
1
1.航天员景海鹏和陈冬进入天宫二号,开展相关空间科学试验。航天员测出天宫二号绕地球做匀速圆周运动的周期为T,距地面的高度为h,已知地球半径为R,引力常量为G,不考虑地球的自转。求: (1)地球的平均密度; (2)地球表面的重力加速度。 2.2019年1月3日,我国“嫦娥四号”探测器成功着陆在月球背面预选着陆区,月球车“玉兔二号”到达月面开始巡视探测,对研究月球和太阳系早期历史具有重要价值。已知地球半径为R,地球表面的重力加速度大小为g,月球半径是地球的,质量是地球的,着陆前探测器在距月面高度为h的环月轨道上做圆周运动。求: (1)月球表面处重力加速度的大小; (2)探测器在环月轨道上做圆周运动的周期T。 3.宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处。(取地球表面重力加速度g1=10m/s2,空气阻力不计, 该星球的半径与地球半径之比为R星∶R地=1∶4) 求: (1) 求该星球表面附近的重力加速度g2; (2) 求该星球的质量与地球质量之比M星∶M地。 4.2021年10月16日,我国成功发射了神舟十三号载人飞船,与空间站组合体完成自主快速交会对接,3名航天员翟志刚、王亚平、叶光富成功送入了天和核心舱,他们将在轨驻留6个月,任务主要目标为验证中国空间站建造相关技术,为我国空间站后续建造及运营任务奠定基础。 已知神舟十三号与空间站组合体完成对接后在轨道上运行,可视为匀速圆周运动,它们飞行n圈所用时间为t。已知它们的总质量为m,它们距地面的高度为h,地球半径为R,引力常量为G。求: (1)神舟十三号与空间站组合体对接后,地球对它们的万有引力F; (2)地球的质量M; (3)地球表面的重力加速度g。 5.祝融号火星车在着陆火星之前,需经历动力减速、悬停避障两个阶段。在动力减速阶段可视为匀减速运动,速度大小由96m/s减小到0,历时80s。在悬停避障阶段,火星车将启用最大推力为7500N的变推力发动机,在距火星表面约百米高度处悬停,寻找着陆点。已知火星半径约为地球半径的,火星质量约为地球质量的,地球表面重力加速度大小取10m/s2,求: (1)在动力减速阶段的加速度大小和下降距离; (2)在悬停避障阶段,火星车能借助该变推力发动机实现悬停,若已知火星车质量为240kg,求火星车能携带物资的最大质量。 6.遥远的星球。某星球完全由不可压缩的液态水组成。星球的表面重力加速度为,半径为R,且没有自转。水的密度,万有引力常数。本题中可能用到如下公式:半径为R的球,其体积为,表面积为。 (1)星球的半径R是多少? (2)星球内部的重力加速度为,其中r是到球心的距离。请通过分析画出图。(提示:已知均匀球壳对球壳内部物体的万有引力为零) (3)假定该星球没有大气层,求这个星球中心处由水产生的压强。 7.“嫦娥一号”卫星在距月球表面高度为h处做匀速圆周运动的周期为T,已知月球半径为R,引力常量为G,(球的体积公式,其中R为球的半径)求: (1)月球的质量M; (2)月球表面的重力加速度g月; (3)月球的密度ρ。 8.宇航员在某质量分布均匀的星球表面,以速度v0竖直上抛一质量为m的物体(引力视为恒力,阻力可忽略),经过时间t落到地面。已知该行星半径为R,引力常量为G,忽略星球自转的影响,求: (1)该星球表面的重力加速度大小; (2)该星球的质量; (3)该星球的密度。 9.一个到达月球的宇航员随身携带一质量为1.0kg的物体A,在月球某处他捡起一块岩石B,然后他把A和B用轻绳连接并挂在一个定滑轮上(不计滑轮与绳的摩擦),如图所示,测量得到B下落的加速度为1.2m/s2.已知地球质量约为月球质量的81倍,地球半径约为月球半径倍,地球表面重力加速度约为10m/s2,计算结果均保留两位有效数字。求: (1)月球表面重力加速度约为多少 (2)B的质量约为多少 10.2021年2月,执行我国火星探测任务的“天问一号”探测器在成功实施三次近火制动后,进入近火点为A远火点为B的椭圆轨道上运行,A点距火星表面的高度为、B点距火星表面的高度为,探测器在椭圆轨道上运行的周期为。之后,探测器再经多次变轨,进入环绕火星表面的圆轨道上运行考察。最后,搭载“祝融号”火星车的着陆巡视器成功着陆火星表面。已知火星半径为R,引力常量为G。 (1)求探测器在环火表面圆轨道上运行的周期。 (2)火星着陆巡视器着陆火星的最后阶段,先在高度为h处悬停,关闭发动机后自由下落到火星表面,求其着陆时的速度。 11.如图所示是“月亮女神”、“嫦娥一号”两卫星绕月球做匀速圆周运行时某时刻的图片,用、分别表示“月亮女神”和“嫦娥一号”的周期,用、分别表示月球的半径和“嫦娥一号”的轨道半径。求: (1)月球的平均密度; (2)从图示位置开始,经多少时间两卫星第一次相距最远。 12.“天问一号”是中国首个火星探测器,其名称来源于我国著名爱国主义诗人屈原的长诗《天问》。2021年2月10日19时52分我国首次火星探测任务“天问一号”探测器实施近火捕获制动,成功实现环绕火星运动,成为我国第一颗人造火星卫星。在“天问一号”环绕火星做匀速圆周运动时,周期为,轨道半径为,已知火星的半径为,引力常量为,不考虑火星的自转。求: (1)“天问一号”环绕火星运动的线速度的大小; (2)火星的质量; (3)火星表面的重力加速度的大小。 13.2021年6月11日,天问一号探测器着陆火星首批科学影像图公布。质量为的天问一号在火星表面着陆前的动力减速阶段可看作竖直方向的匀变速直线运动,探测器发动机打开,会在火星表面附近经历一个时长为、速度由减速到零的过程。已知火星半径约为地球半径的二分之一,火星质量约为地球质量的八分之一,地球表面的重力加速度大小为,忽略火星大气阻力。求: (1)火星表面的重力加速度大小; (2)动力减速阶段着陆器受到的制动力大小。 14.我国发射的“嫦娥一号”探月卫星沿近似于圆形的轨道绕月飞行。设卫星距月球表面的高度为h,做匀速圆周运动的周期为T。已知月球半径为R,引力常量为G,球的体积公式。求: (1)月球的质量M; (2)月球表面的重力加速度g月; (3)月球的密度ρ。 15.开普勒第三定律指出:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等,该定律对一切具有中心天体的引力系统都成立。如图所示,已知嫦娥三号探月卫星在半径为r的圆形轨道Ⅰ上绕月球运行,周期为T,月球的半径为R,引力常量为G。某时刻嫦娥三号卫星在A点变轨进入椭圆轨道Ⅱ,在月球表面的B点着陆。A、O、B三点在一条直线上。求: (1)月球的密度; (2)探月卫星在轨道Ⅱ上从A点运动到B点所用的时间。 16.假设宇航员在质量为M,半径为R的某星球表面做了一个实验:将一个质量为m的物体置于半径为r的水平圆盘边缘,物体与圆盘间的动摩擦因数为μ,使圆盘绕过圆心的竖直轴转动,转速缓慢增加,某时刻物体从圆盘上滑出,经时间t落地。设引力常量为G;物体与圆盘间的最大静摩擦力等于滑动摩擦力。 求:(1)该星球表面的重力加速度大小; (2)物体离开圆盘时的速度大小; (3)落地点到圆盘圆心的水平距离。 17.2020年12月6日5时42分,嫦娥五号上升器成功与轨道器返回器组合体交会对接,并于6时12分将月球样品容器安全转移至返回器中。如图所示,返回式月球软着陆器在完成了对月球表面的考察任务后,由月球表面回到绕月球做圆周运动的轨道舱。已知月球表面的重力加速度为g,月球的半径为R,轨道舱到月球中心的距离为r,引力常量为G,不考虑月球的自转。求: (1)月球的质量M; (2)轨道舱绕月飞行的周期T。 18.2021年5月29日晚8时55分,中国“天舟二号”货运飞船从文昌航天发射场升空,飞船顺利进入预定轨道。5月30日上午5时01分,天舟二号货运飞船与天和核心舱交会对接,对接过程示意图如图所示。已知对接后的组合体沿圆形轨道运行,经过时间t,组合体绕地球球心转过的角度为,地球半径为R,地球表面重力加速度为g,引力常量为G,不考虑地球自转。求: (1)地球质量M; (2)组合体所在圆轨道距地面的高度H。 19.2021年5月15日,“天问一号”着陆巡视器成功着陆于火星乌托邦平原南部预选着陆区,我国首次火星探测任务着陆火星取得圆满成功。“天问一号”着陆巡视器质量为,其在火星表面着陆前的动力减速阶段可视为在竖直方向做匀变速直线运动,探测器制动打开后,会在火星表面附近经历一个时长为、速度由减速到零的过程。已知火星半径约为地球半径的二分之一,火星质量约为地球质量的十分之一,地球表面的重力加速度为,忽略火星大气阻力。求: (1)火星表面的重力加速度大小; (2)着陆巡视器在火星表面着陆前的动力减速阶段受到的制动力大小。 20.我国首次火星探测任务天问一号探测器在火星乌托邦平原南部预选着陆区着陆,迈出了我国星际探测征程的重要一步。探测器着陆前绕火星做匀速圆周运动,距火星表面的高度为h,做匀速圆周运动的角速度为ω,已知火星的半径为R,引力常量为G,(题中的字母是已知量),求: (1)火星的质量M的表达式; (2)火星表面的重力加速度g的表达式。 参考答案 1.(1);(2) 【解析】 (1)设地球质量为M,飞船质量为m 对飞船 联立得 (2)对地表上物体 联立得 2.(1);(2) 【解析】 (1)对于地球和月球表面的物体m,其重力近似等于万有引力,设地球质量为M,月球质量和半径分别为、,则 又 , 解得 (2)设探测器的质量为,其受到的万有引力提供向心力,则 又 ,, 解得 3.(1);(2) 【解析】 (1)竖直上抛运动的总时间 因为初速度相同,时间之比为1:5,所以星球表面的重力加速度 (2)设星球表面有一物体质量为m,则 所以 即 4.(1);(2);(3) 【解析】 (1)组合体绕地球运动的周期 则所受的万有引力为 (2) 根据万有引力等于向心力 解得地球的质量 (3)根据 解得 5.(1)1.2m/s2,3840m;(2)1635kg 【解析】 (1)在动力减速阶段所用时间为t,初速度大小为v1,末速度大小为v2,加速度大小为a,由匀变速直线运动速度公式有 代入题给数据得 设探测器下降的距离为s,由匀变速直线运动位移公式有 代入数据联立解得 (2)设火星的质量、半径和表面重力加速度大小分别为M火、r火和g火,地球的质量、半径和表面重力加速度大小分别为M地、r地和g地由牛顿运动定律和万有引力定律,对质量为m的物体有 式中G为引力常量。设变推力发动机的最大推力为F,能够悬停的火星车加物资最大质量为,由力的平衡条件有 代入数据联立解得 在悬停阶段,该变推力发动机能实现悬停携带物资最大质量约为 6.(1);(2) ;(3) 【解析】 (1)星球表面,万有引力等于重力 星球的质量 又 代入数据联立解得 (2)星球内部距球心处的重力加速度 则其图像为 (3)星球内部任意半径r处的重力加速度 现在做一根从星体表面到球心的细长的圆柱体液柱,圆柱体截面积是s,s非常小,星球中心的压力就是这个液柱的重力。因为液柱两侧的其他液体给予的力是垂直侧面的,没有径向分量,处液体体积元 则所受重力为 从球心处到星球表面重力积分为 则压强为 代入数据得 7.(1);(2);(3) 【解析】 (1)设“嫦娥一号”质量为m,根据牛顿第二定律有 ① 解得 ② (2)月球表面质量为m0的物体所受重力等于万有引力,即 ③ 联立②③解得 ④ (3)根据密度公式可得 ⑤ 8.(1);(2);(4) 【解析】 (1)设行星表面的重力加速度为,对小球,有 解得 (2)对行星表面的物体,有 故行星质量 (3)故行星的密度 可得 9.(1)1.7m/s2;(2)5.8kg 【解析】 (1)由 得 代入数据,可得 (2)对A、B利用牛顿第二定律得 解得 mB=5.8kg 10.(1);(2) 【解析】 (1)根据开普勒第三定律 解得 (2)在火星表面绕火星做圆周运动时 根据自由落体运动规律 解得 11.(1) ;(2) 【解析】 (1)设月球的质量为, 嫦娥一号的质量为,有 又 联立解得 (2)设经过时间两卫星第一次相距最远,有 解得 12.(1);(2);(3) 【解析】 (1)由线速度定义可得 (2)设“天问一号”的质量为m,引力提供向心力有 得 (3)忽略火星自转,火星表面质量为的物体,其所受引力等于重力 得 13.(1);(2) 【解析】 (1)由 解得火星表面的重力加速度与地球表面重力加速度的比值 即火星表面的重力加速度 (2)着陆器着陆过程可视为竖直向下的匀减速直线运动,由 可得 由牛顿第二定律有 解得此过程中着陆器受到的制动力大小 14.(1) ;(2) ;(3) 【解析】 (1)对卫星,由万有引力提供向心力,则 得 (2)假设月球表面附近有一物体m1,其所受万有引力等于其重力,则 解得 (3)根据 求得 15.(1);(2) 【解析】 (1)由万有引力充当向心力有 解得 月球的密度 解得 (2)椭圆轨道的半长轴 设椭圆轨道上运行周期为,由开普勒第三定律有 在轨道Ⅱ上运行的时间为 解得 16.(1);(2);(3) 【解析】 (1)由 得 (2)由 得 (3)水平射程 落地点到圆心的水平距离 17.(1);(2) 【解析】 (1)设月球表面上质量为m1的物体,其在月球表面有 月球质量 (2)轨道舱绕月球做圆周运动,设轨道舱的质量为m,由牛顿运动定律得 解得 18.(1);(2) 【解析】 (1)地球表面的万有引力等于重力 解得 (2)组合体运行的角速度 万有引力提供向心力 解得 19.(1);(2) 【解析】 (1)由 解得火星表面的重力加速度与地球表面重力加速度的比值 即火星表面的重力加速度 (2)着陆巡视器着陆过程可视为竖直向下的匀减速直线运动 由 可得 由牛顿第二定律有 解得此过程中着陆巡视器受到的制动力大小 20.(1);(2) 【解析】 (1)设探测器的质量为m,由万有引力提供向心力有 解得火星的质量 (2)设火星表面的物体质量为m1,物体受到的万有引力近似等于重力 联立解得
1
