华东师大版八年级下册数学 19.1.2 矩形的判定 课件(共16张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.1.2 矩形的判定 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 296.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
矩形的判定
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探究矩形的判定吧.
情景导入
思考
学习目标
1.探索并证明矩形的判定定理.(重点)
2.能应用矩形的判定解答简单的证明题和计算题.(难点)
定义:有一个角是直角的平行四边形叫做矩形。
矩形的定义是什么?
问题
(类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法)
除了定义以外,判定矩形还有其他的方法吗?
问题
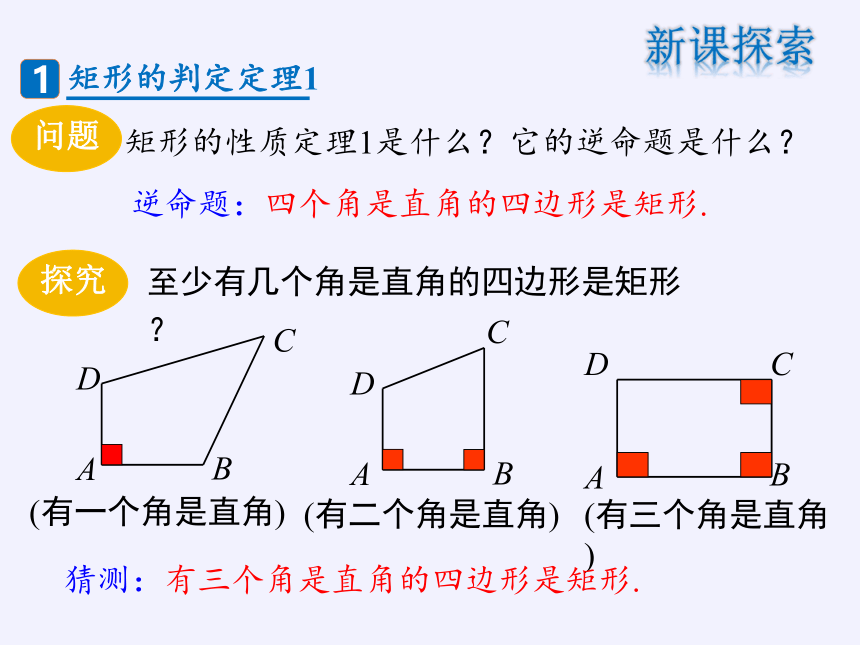
矩形的性质定理1是什么?它的逆命题是什么?
逆命题:四个角是直角的四边形是矩形.
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
新课探索
问题
至少有几个角是直角的四边形是矩形?
探究
1
矩形的判定定理1
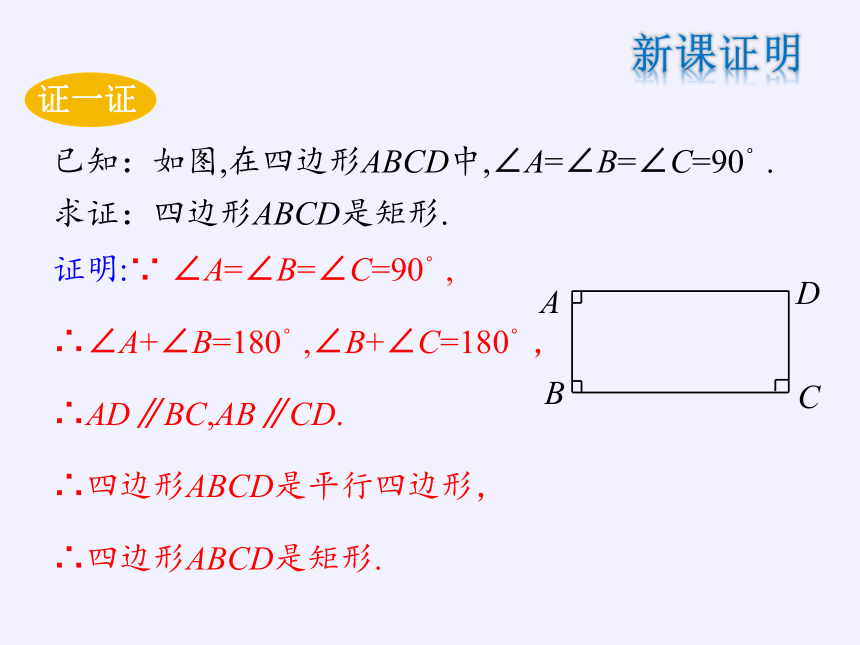
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
A
B
C
D
新课证明
证一证
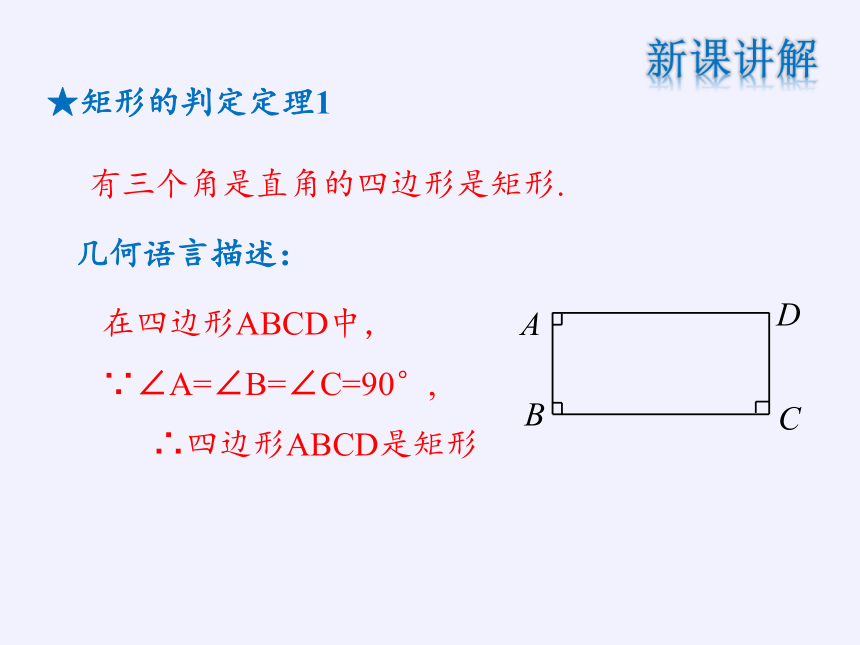
有三个角是直角的四边形是矩形.
几何语言描述:
A
B
C
D
新课讲解
★矩形的判定定理1
在四边形ABCD中,∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形
逆命题:对角线相等且互相平分的四边形是矩形。
新课讲解
2
矩形的判定定理2
矩形关于对角线的性质是什么?它的逆命题是什么?
问题
问题
可以改写为:对角线相等的平行四边形是矩形。
9
对角线相等的平行四边形是矩形
新课探索
通过课本P103“试一试”的操作可以得到:
已知:如图,在□ABCD中,AC 、 DB是它的两条对角
线, AC=DB.求证:□ABCD是矩形.
A
B
C
D
新课证明
证一证
证明:∵四边形ABCD是平行四边形
∴AB = DC,BC = CB
∵AC = DB,
∴ △ABC≌△DCB ,
∴∠ABC = ∠DCB.
∵AB∥CD,
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ □ ABCD是矩形(矩形的定义).
对角线相等的平行四边形是矩形.
几何语言描述:
在平行四边形ABCD中,∵AC=BD,
∴平行四边形ABCD是矩形.
A
B
C
D
新课讲解
★矩形的判定定理2
判断正误,如若有误请说明理由。
(1)对角线相等的四边形是矩形.
(2)对角线互相平分且相等的四边形是矩形.
(3)有一个角是直角的四边形是矩形.
(5)有三个角是直角的四边形是矩形.
(6)四个角都相等的四边形是矩形.
(4)有三个角都相等的四边形是矩形.
×
×
×
√
√
√
随堂即练
例1:如图,平行四边形ABCD中,对角线AC、BD相交于点O,延长OA到N,使ON=OB,再延长OC至M,
使CM=AN.求证:四边形NDMB为矩形.
证明:∵四边形ABCD为平行四边形
∴AO=OC OD=OB
∵AN=CM
∴AO+AN=OC+CM
∴ON=OM
∴四边形NDMB为平行四边形
∵ON=OB
∴2ON=2OB 即MN=BD
∵平行四边形NDMB为矩形
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
运用定理进行计算和证明
矩形的判定
定义
判定定理
课堂总结
有一个角是直角的平行四边形是矩形
通过本节课你学到了什么?
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
解决问题
思考
你会了吗
谢 谢
矩形的判定
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探究矩形的判定吧.
情景导入
思考
学习目标
1.探索并证明矩形的判定定理.(重点)
2.能应用矩形的判定解答简单的证明题和计算题.(难点)
定义:有一个角是直角的平行四边形叫做矩形。
矩形的定义是什么?
问题
(类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法)
除了定义以外,判定矩形还有其他的方法吗?
问题
矩形的性质定理1是什么?它的逆命题是什么?
逆命题:四个角是直角的四边形是矩形.
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
新课探索
问题
至少有几个角是直角的四边形是矩形?
探究
1
矩形的判定定理1
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
A
B
C
D
新课证明
证一证
有三个角是直角的四边形是矩形.
几何语言描述:
A
B
C
D
新课讲解
★矩形的判定定理1
在四边形ABCD中,∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形
逆命题:对角线相等且互相平分的四边形是矩形。
新课讲解
2
矩形的判定定理2
矩形关于对角线的性质是什么?它的逆命题是什么?
问题
问题
可以改写为:对角线相等的平行四边形是矩形。
9
对角线相等的平行四边形是矩形
新课探索
通过课本P103“试一试”的操作可以得到:
已知:如图,在□ABCD中,AC 、 DB是它的两条对角
线, AC=DB.求证:□ABCD是矩形.
A
B
C
D
新课证明
证一证
证明:∵四边形ABCD是平行四边形
∴AB = DC,BC = CB
∵AC = DB,
∴ △ABC≌△DCB ,
∴∠ABC = ∠DCB.
∵AB∥CD,
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ □ ABCD是矩形(矩形的定义).
对角线相等的平行四边形是矩形.
几何语言描述:
在平行四边形ABCD中,∵AC=BD,
∴平行四边形ABCD是矩形.
A
B
C
D
新课讲解
★矩形的判定定理2
判断正误,如若有误请说明理由。
(1)对角线相等的四边形是矩形.
(2)对角线互相平分且相等的四边形是矩形.
(3)有一个角是直角的四边形是矩形.
(5)有三个角是直角的四边形是矩形.
(6)四个角都相等的四边形是矩形.
(4)有三个角都相等的四边形是矩形.
×
×
×
√
√
√
随堂即练
例1:如图,平行四边形ABCD中,对角线AC、BD相交于点O,延长OA到N,使ON=OB,再延长OC至M,
使CM=AN.求证:四边形NDMB为矩形.
证明:∵四边形ABCD为平行四边形
∴AO=OC OD=OB
∵AN=CM
∴AO+AN=OC+CM
∴ON=OM
∴四边形NDMB为平行四边形
∵ON=OB
∴2ON=2OB 即MN=BD
∵平行四边形NDMB为矩形
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
运用定理进行计算和证明
矩形的判定
定义
判定定理
课堂总结
有一个角是直角的平行四边形是矩形
通过本节课你学到了什么?
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
解决问题
思考
你会了吗
谢 谢
