2.1.2空间中直线与直线之间的位置关系(下)
文档属性
| 名称 | 2.1.2空间中直线与直线之间的位置关系(下) |  | |
| 格式 | zip | ||
| 文件大小 | 194.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-30 09:20:40 | ||
图片预览



文档简介
课件24张PPT。2.1.2空间中直线与直线
之间的位置关系(下)湖南省耒阳市振兴学校
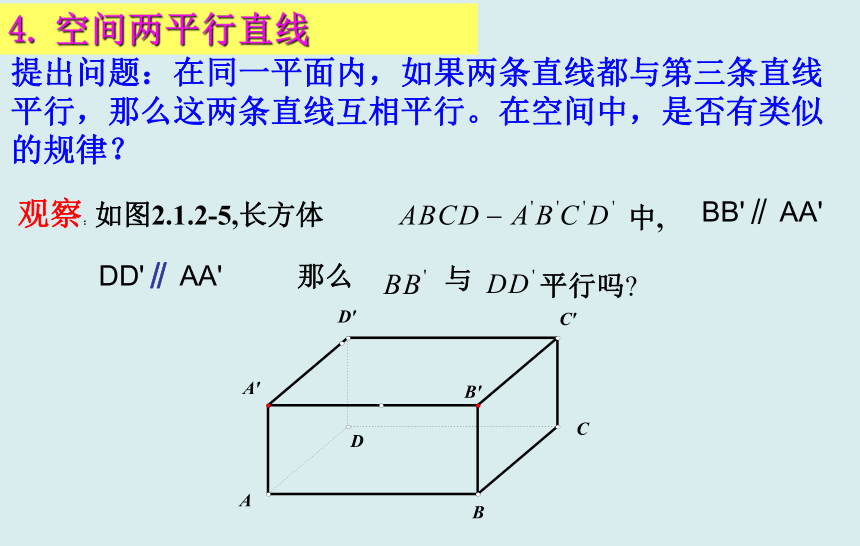
高中数学老师欧阳文丰制作4.?空间两平行直线提出问题:在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相平行。在空间中,是否有类似的规律?公理4:平行于同一条直线的两条直线互相平行。公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。公理4作用:判断空间两条直线平行的依据。a∥b
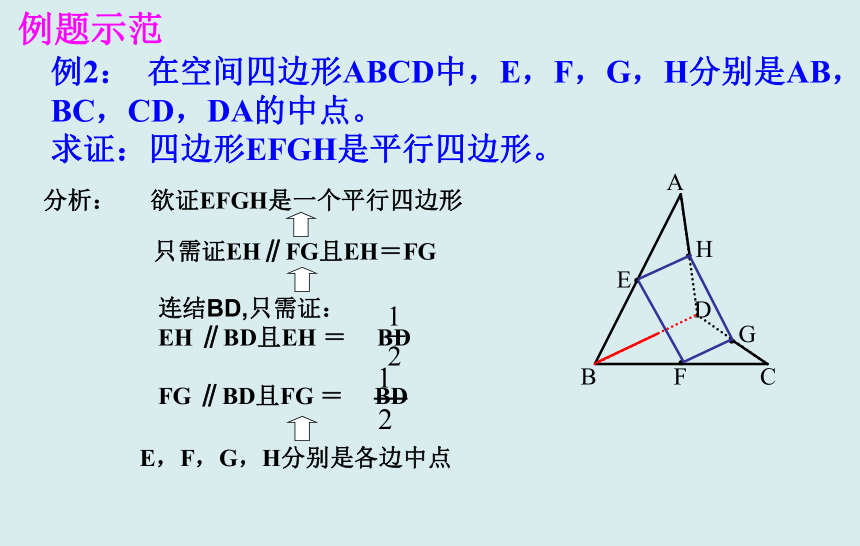
c∥ba∥c符号表示:设空间中的三条直线分别为a, b, c,若想一想:空间中,如果两条直线都与第三条直线垂直,是否也有类似的规律?问:垂直于同一条直线的两条直线,有几种位置关系——有三种:相交,平行,异面例题示范例2: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。分析:欲证EFGH是一个平行四边形只需证EH∥FG且EH=FGE,F,G,H分别是各边中点连结BD,只需证:
EH ∥BD且EH = BD
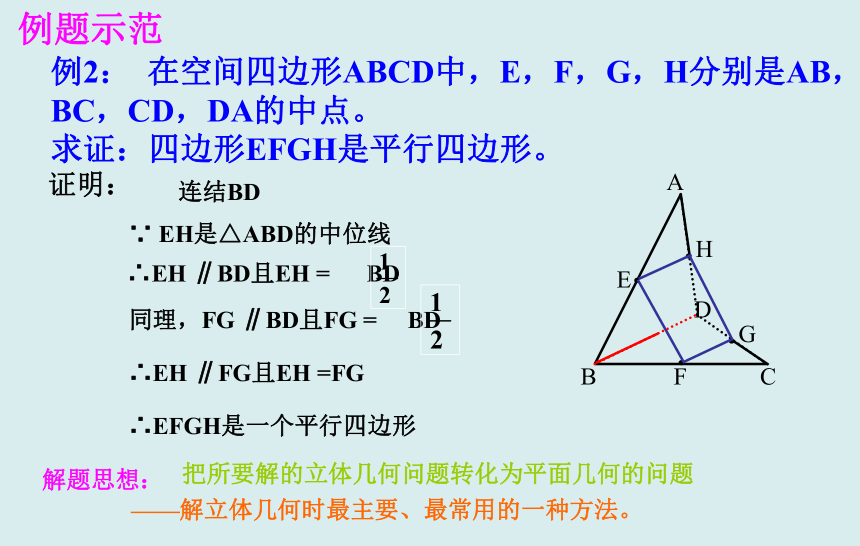
FG ∥BD且FG = BD例题示范例2: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
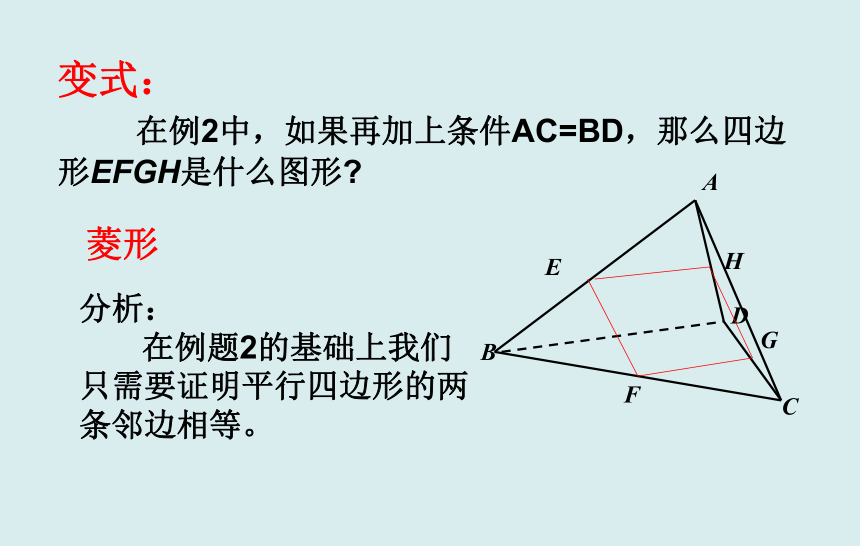
求证:四边形EFGH是平行四边形。解题思想:把所要解的立体几何问题转化为平面几何的问题——解立体几何时最主要、最常用的一种方法。变式: 在例2中,如果再加上条件AC=BD,那么四边形EFGH是什么图形? EHFG分析:
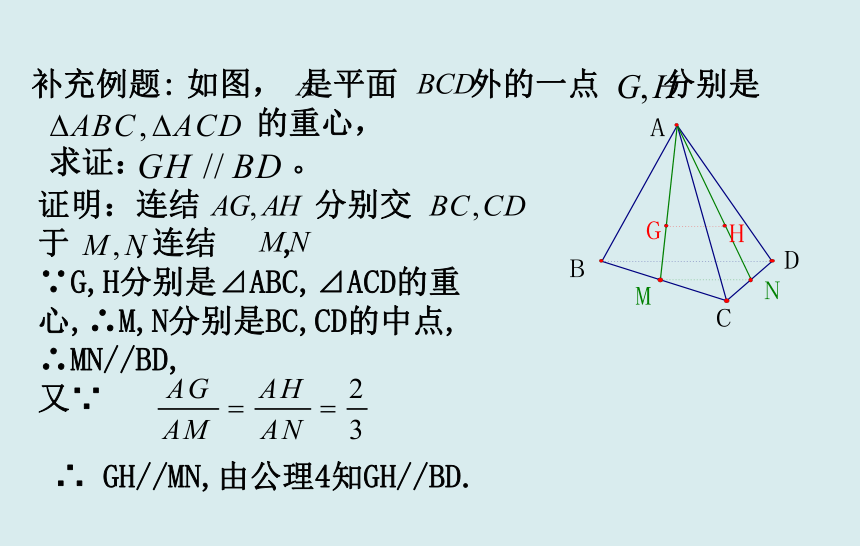
在例题2的基础上我们只需要证明平行四边形的两条邻边相等。菱形补充例题:?如图, 是平面 外的一点 分别是
的重心,
求证: 。 证明:连结 分别交
于 ,连结 ,
∵G,H分别是⊿ABC,⊿ACD的重心,∴M,N分别是BC,CD的中点,
∴MN//BD,
又∵
∴ GH//MN,由公理4知GH//BD.
练习:1.判断题
(1)平行于同一直线的两条直线平行 . ( )
(2)垂直于同一直线的两条直线平行 . ( )
(3)过直线外一点,有且只有一条直线与已知直线平行 . ( )
(4)与已知直线平行且距离等于定长的直线只有两条. ( ) √√××2.选择题
(1)分别在两个平面内的两条直线间的位置关系是( )
(A)异面 (B)平行 (C)相交 (D)以上都有可能
(2)长方体的一条对角线与长方体的棱所组成的异面直线有 ( )
(A)2对 (B)3对 (C)6对 (D)12对
(3)两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是( )
(A)一定是异面直线 (B)一定是相交直线
(C)可能是平行直线 (D)可能是异面直线,也可能是相交直线
(4)一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是( )
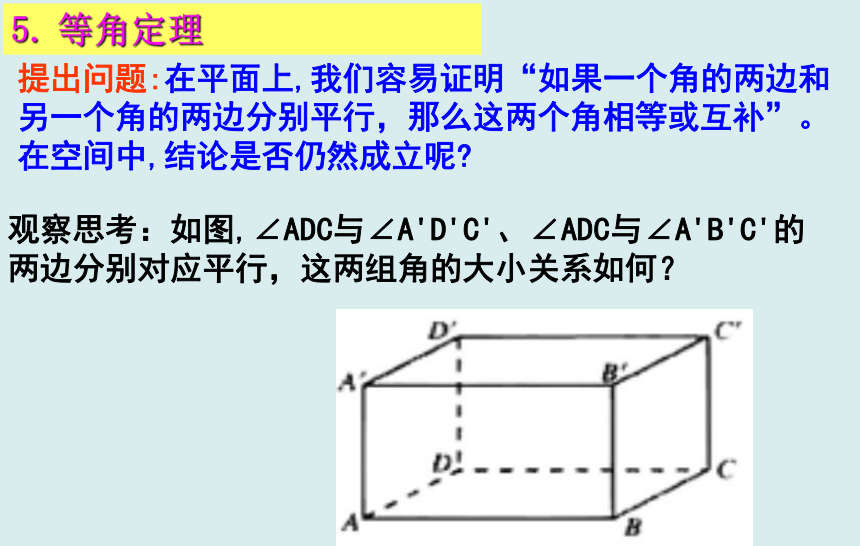
(A)平行 (B)相交 (C)异面 (D)相交或异面 D C A D 5.?等角定理提出问题:在平面上,我们容易证明“如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补”。在空间中,结论是否仍然成立呢?观察思考:如图,∠ADC与∠A'D'C'、∠ADC与∠A'B'C'的两边分别对应平行,这两组角的大小关系如何?等角定理1:如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补.推论1:如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等.5、等角定理推论2:如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等.6.?异面直线所成的角如图,已知两条异面直线a,b,经过空间任一点O作直线a'∥a,b'∥b,我们把a'与b'所成的锐角(或直角)叫做异面直线a,b所成的角(或夹角)。为了简便,点O通常取在两条异面直线中的一条上,例如,取在直线b上,然后经过点O作直线a'∥a,a'?和b所成的锐角(或直角)就是异面直线a与b所成的角。想一想:a'与b'?所成角的大小与点O的位置有关吗?6.?异面直线所成的角如果两条异面直线所成的角为直角,就说两条直线互相垂直,记作a⊥b。两条异面直线所成角的范围为
与两条异面直线的都垂直的直线叫做两条异面直线的公垂线
则两异面直线的公垂线有几条?
两条直线互相垂直,它们一定相交吗?(00,900]有且只有一条不一定,还可能异面探究:右图中有没有两条棱所在的直线是互相垂直的异面直线?
请说出其中的3对 垂直于同一条直线的两条直线是否平行 ——不一定,可能是平行直线,也可能是相交直线,也可能是异面直线。请对照右图说明。如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直?一定垂直例题示范例3、如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA‘?和CC’?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直? 解:(1)由异面直线的判定方法可知,与直线成异面直线的有直线,例题示范解:(2)由 可知,
等于异面直线 与 的夹角,所以异面直线 BA '和CC’
的夹角为450 。 (3) 直线分别与直线 都垂直.例3、如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA '和CC’?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直? 求两条异面直线所成的角的一般步骤:(1)构造:根据异面直线的定义,用平移法(常用三角形中位线、平行四边形性质)作出异面直线所成的角。(2)证明:证明作出的角就是要求的角.(3)计算:求角度,常利用三角形(4)结论:若求出的角是锐角或指教,则它就是所求异面直线补充例题 如图,在长方体中,已知AA1=AD=a,
AB= a,求AB1与BC1所成的角的余弦值.CBADA1B1C1D1aa练习反馈:1. 判断:
(1)平行于同一直线的两条直线平行.( )
(2)垂直于同一直线的两条直线平行.( ?)
(3)过直线外一点,有且只有一条直线与已知直线平行?.?( )
(4)与已知直线平行且距离等于定长的直线只有两条.????( )
(5)若一个角的两边分别与另一个角的两边平行,那么这两个角相等( )
(6)若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.?(???)????√×√√××练习反馈:2.选择题
?(1)“a,b是异面直线”是指?①?a∩b=Φ,且a不平行于b;②?a ì平面a,bì平面b且a∩b=Φ ③?a?ì平面a,b??平面a?④?不存在平面a,能使a?ìa且b?ìa成立
上述结论中,正确的是 (???)
(A)①② (B)①③ (C)①④ (D)③④(2)长方体的一条对角线与长方体的棱所组成的异面直线有 (???)
?(A)2对 (B)3对 (C)6对 (D)12对CC(3)两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是(??)
?(A)一定是异面直线 (B)一定是相交直线
?(C)可能是平行直线
(D)可能是异面直线,也可能是相交直线
(4)一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是(? )
(A)平行 (B)相交
(C)异面 (D)相交或异面3.两条直线互相垂直,它们一定相交吗????答:不一定,还可能异面.DD4.垂直于同一直线的两条直线,有几种位置关系?答:三种:相交,平行,异面.5.画两个相交平面,在这两个平面内各画一条直线使它们成为(1)平行直线;(2)相交直线;(3)异面直线.6.选择题
?(1)分别在两个平面内的两条直线间的位置关系是 (? )
?(A)异面 (B)平行
(C)相交 (D)以上都有可能??
(2)异面直线a,b满足a?ìa,b?ìb,a∩b=l,
则l与a,b的位置关系一定是(? )(A)l至多与a,b中的一条相交;
(B)l至少与a,b中的一条相交;
(C)l与a,b都相交;
(D)l至少与a,b中的一条平行.DB(3)两异面直线所成的角的范围是 ( )
(A)(0°,90°) (B)[0°,90°)
(C)(0°,90°] (D)[0°,90°]7.判断下列命题的真假,真的打“√”,假的打“×”
?(1)两条直线和第三条直线成等角,则这两条直线平行???????????(???)
?(2)平行移动两条异面直线中的任一条,它们所成的角不变???????(??)
?(3)四边相等且四个角也相等的四边形是正方形?????????????????(???)C×√×课堂小结:作业布置:
P51 A组3、4(1)(2)(3)、5、6.
之间的位置关系(下)湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作4.?空间两平行直线提出问题:在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相平行。在空间中,是否有类似的规律?公理4:平行于同一条直线的两条直线互相平行。公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。公理4作用:判断空间两条直线平行的依据。a∥b
c∥ba∥c符号表示:设空间中的三条直线分别为a, b, c,若想一想:空间中,如果两条直线都与第三条直线垂直,是否也有类似的规律?问:垂直于同一条直线的两条直线,有几种位置关系——有三种:相交,平行,异面例题示范例2: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。分析:欲证EFGH是一个平行四边形只需证EH∥FG且EH=FGE,F,G,H分别是各边中点连结BD,只需证:
EH ∥BD且EH = BD
FG ∥BD且FG = BD例题示范例2: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。解题思想:把所要解的立体几何问题转化为平面几何的问题——解立体几何时最主要、最常用的一种方法。变式: 在例2中,如果再加上条件AC=BD,那么四边形EFGH是什么图形? EHFG分析:
在例题2的基础上我们只需要证明平行四边形的两条邻边相等。菱形补充例题:?如图, 是平面 外的一点 分别是
的重心,
求证: 。 证明:连结 分别交
于 ,连结 ,
∵G,H分别是⊿ABC,⊿ACD的重心,∴M,N分别是BC,CD的中点,
∴MN//BD,
又∵
∴ GH//MN,由公理4知GH//BD.
练习:1.判断题
(1)平行于同一直线的两条直线平行 . ( )
(2)垂直于同一直线的两条直线平行 . ( )
(3)过直线外一点,有且只有一条直线与已知直线平行 . ( )
(4)与已知直线平行且距离等于定长的直线只有两条. ( ) √√××2.选择题
(1)分别在两个平面内的两条直线间的位置关系是( )
(A)异面 (B)平行 (C)相交 (D)以上都有可能
(2)长方体的一条对角线与长方体的棱所组成的异面直线有 ( )
(A)2对 (B)3对 (C)6对 (D)12对
(3)两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是( )
(A)一定是异面直线 (B)一定是相交直线
(C)可能是平行直线 (D)可能是异面直线,也可能是相交直线
(4)一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是( )
(A)平行 (B)相交 (C)异面 (D)相交或异面 D C A D 5.?等角定理提出问题:在平面上,我们容易证明“如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补”。在空间中,结论是否仍然成立呢?观察思考:如图,∠ADC与∠A'D'C'、∠ADC与∠A'B'C'的两边分别对应平行,这两组角的大小关系如何?等角定理1:如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补.推论1:如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等.5、等角定理推论2:如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等.6.?异面直线所成的角如图,已知两条异面直线a,b,经过空间任一点O作直线a'∥a,b'∥b,我们把a'与b'所成的锐角(或直角)叫做异面直线a,b所成的角(或夹角)。为了简便,点O通常取在两条异面直线中的一条上,例如,取在直线b上,然后经过点O作直线a'∥a,a'?和b所成的锐角(或直角)就是异面直线a与b所成的角。想一想:a'与b'?所成角的大小与点O的位置有关吗?6.?异面直线所成的角如果两条异面直线所成的角为直角,就说两条直线互相垂直,记作a⊥b。两条异面直线所成角的范围为
与两条异面直线的都垂直的直线叫做两条异面直线的公垂线
则两异面直线的公垂线有几条?
两条直线互相垂直,它们一定相交吗?(00,900]有且只有一条不一定,还可能异面探究:右图中有没有两条棱所在的直线是互相垂直的异面直线?
请说出其中的3对 垂直于同一条直线的两条直线是否平行 ——不一定,可能是平行直线,也可能是相交直线,也可能是异面直线。请对照右图说明。如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直?一定垂直例题示范例3、如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA‘?和CC’?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直? 解:(1)由异面直线的判定方法可知,与直线成异面直线的有直线,例题示范解:(2)由 可知,
等于异面直线 与 的夹角,所以异面直线 BA '和CC’
的夹角为450 。 (3) 直线分别与直线 都垂直.例3、如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA '和CC’?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直? 求两条异面直线所成的角的一般步骤:(1)构造:根据异面直线的定义,用平移法(常用三角形中位线、平行四边形性质)作出异面直线所成的角。(2)证明:证明作出的角就是要求的角.(3)计算:求角度,常利用三角形(4)结论:若求出的角是锐角或指教,则它就是所求异面直线补充例题 如图,在长方体中,已知AA1=AD=a,
AB= a,求AB1与BC1所成的角的余弦值.CBADA1B1C1D1aa练习反馈:1. 判断:
(1)平行于同一直线的两条直线平行.( )
(2)垂直于同一直线的两条直线平行.( ?)
(3)过直线外一点,有且只有一条直线与已知直线平行?.?( )
(4)与已知直线平行且距离等于定长的直线只有两条.????( )
(5)若一个角的两边分别与另一个角的两边平行,那么这两个角相等( )
(6)若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.?(???)????√×√√××练习反馈:2.选择题
?(1)“a,b是异面直线”是指?①?a∩b=Φ,且a不平行于b;②?a ì平面a,bì平面b且a∩b=Φ ③?a?ì平面a,b??平面a?④?不存在平面a,能使a?ìa且b?ìa成立
上述结论中,正确的是 (???)
(A)①② (B)①③ (C)①④ (D)③④(2)长方体的一条对角线与长方体的棱所组成的异面直线有 (???)
?(A)2对 (B)3对 (C)6对 (D)12对CC(3)两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是(??)
?(A)一定是异面直线 (B)一定是相交直线
?(C)可能是平行直线
(D)可能是异面直线,也可能是相交直线
(4)一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是(? )
(A)平行 (B)相交
(C)异面 (D)相交或异面3.两条直线互相垂直,它们一定相交吗????答:不一定,还可能异面.DD4.垂直于同一直线的两条直线,有几种位置关系?答:三种:相交,平行,异面.5.画两个相交平面,在这两个平面内各画一条直线使它们成为(1)平行直线;(2)相交直线;(3)异面直线.6.选择题
?(1)分别在两个平面内的两条直线间的位置关系是 (? )
?(A)异面 (B)平行
(C)相交 (D)以上都有可能??
(2)异面直线a,b满足a?ìa,b?ìb,a∩b=l,
则l与a,b的位置关系一定是(? )(A)l至多与a,b中的一条相交;
(B)l至少与a,b中的一条相交;
(C)l与a,b都相交;
(D)l至少与a,b中的一条平行.DB(3)两异面直线所成的角的范围是 ( )
(A)(0°,90°) (B)[0°,90°)
(C)(0°,90°] (D)[0°,90°]7.判断下列命题的真假,真的打“√”,假的打“×”
?(1)两条直线和第三条直线成等角,则这两条直线平行???????????(???)
?(2)平行移动两条异面直线中的任一条,它们所成的角不变???????(??)
?(3)四边相等且四个角也相等的四边形是正方形?????????????????(???)C×√×课堂小结:作业布置:
P51 A组3、4(1)(2)(3)、5、6.
