2.6.2一元一次不等式(组)的应用 课件(共41张PPT)
文档属性
| 名称 | 2.6.2一元一次不等式(组)的应用 课件(共41张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-14 00:00:00 | ||
图片预览









文档简介
(共41张PPT)
北师大版八年级下册数学
第二章 一元一次不等式与一元一次不等式组
2.6.2一元一次不等式(组)的应用
一元一次方程解实际问题的步骤 :
实际问题
设未知数
找相等关系
列出方程
检验解的合理性
解方程
交流 : 那么如何用一元一次不等式解实际问题呢 ?
复习引入
一、一元一次不等式的应用
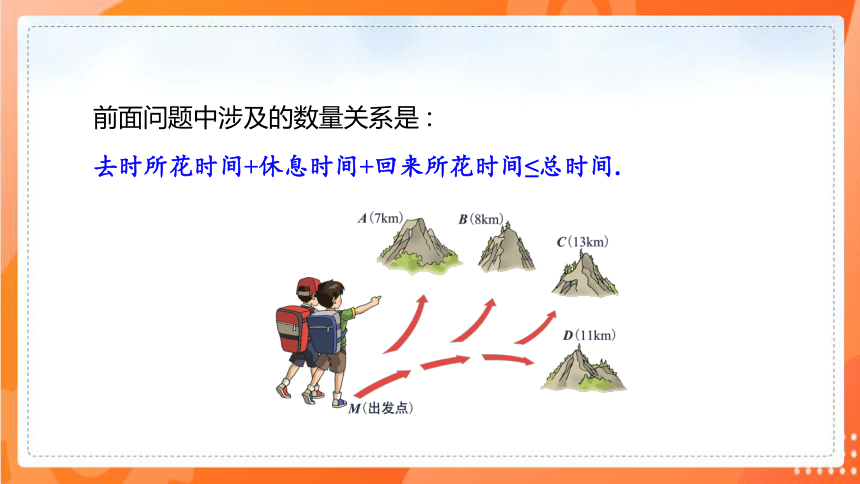
小华打算在星期天与同学去登山 , 计划上午7点出发 , 到达山顶后休息2h , 下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h , 回来时的平均速度是4km/h , 他们最远能登上哪座山顶〔图中数字表示出发点到山顶的路程〕 ?
前面问题中涉及的数量关系是 :
去时所花时间+休息时间+回来所花时间≤总时间.
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h,回来所花时间为 h.
他们在山顶休息了2 h , 又上午7点到下午4点之间总共相隔9 h , 即所用时间应小于或等于9 h.
所以有 +2+ ≤ 9.
解得 x≤12.
因此要满足下午4点以前必须返回出发点 , 小华他们最远能登上D山顶.
x ≥ 125.
例1 某童装店按每套90元的价格购进40套童装 , 应缴纳的税费为销售额的10%. 如果要获得900元的纯利润 , 每套童装的售价至少是多少元 ?
解 : 设每套童装的售价是 x 元.
那么 40x-90×40-40x·10%≥900.
解得
答 : 每套童装的售价至少是125元.
分析 : 此题涉及的数量关系是 :
销售额-成本-税费≥纯利润(900元).
典例精析
例2 当一个人坐下时 , 不宜提举超过4.5 kg的重物 , 以免受伤. 小明坐在书桌前 , 桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本 ?
解: 设小明应搬动x本记事本 , 那么
解得 x≤5.25.
x≤4.5.
答 : 小明最多只应搬动5本记事本.
由于记事本的数目必须是整数 , 所以x 的最大值为5.
解:设小明家每月用水x立方米.
∵5×1.8=9<15 ,
∴小明家每月用水超过5立方米 ,
那么超出(x-5)立方米 , 按每立方米2元收费 ,
列出不等式为 : 5×1.8+(x-5)×2≥15 ,
解不等式得 : x≥8.
答 : 小明家每月用水量至少是8立方米.
例3 小明家每月水费都不少于15元 , 自来水公司的收费标准如下 : 假设每户每月用水不超过5立方米 , 那么每立方米收费1.8元 ; 假设每户每月用水超过5立方米 , 那么超出部分每立方米收费2元 , 小明家每月用水量至少是多少 ?
例4 甲、乙两超市以同样价格出售同样的商品 , 并且给出了差别的优惠方案 : 在甲超市累计购物超过100元后 , 超出100元的部分按90%收费 ; 在乙超市累计购物超过50元后 , 超出50元的部分按95%收费. 顾客到哪家超市购物花费少 ?
分析:甲乙两超市的优惠价格不一样 , 因此需要分类讨论 :
(1)当购物不超过50元 ;
(2)当购物超过50元而不超过100元,
(3)当购物超过100元.
解:(1)当购物不超过50元时,在甲、乙两超市都不享受优惠 , 购物花费一样 ;
(2)当购物超过50元而不超过100元时,在乙超市享受优惠 , 购物花费少;
(3)当累计购物超过100元后 , 设购物为x(x>100)元
①假设 50+0.95(x-50)>100+0.9(x-100) 即x>150
在甲超市购物花费少;
②假设 50+0.95(x-50)<100+0.9(x-100) 即x<150
在乙超市购物花费少;
③假设 50+0.95(x-50)=100+0.9(x-100) 即x=150
在甲、乙两超市购物花费一样.
去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%. 那么明年空气质量良好的天数比去年至少要增加多少?
1
分析:
“明年这样的比值要超过70%”指出了这个问題
中蕴含的不等关系. 转化为不等式,即
练一练
解:
设明年比去年空气质量良好的天数增加了x.
去年有365×60%天空气质量良好,明年有
(x+365×60%)天空气质量良好,并且
去分母,得 x+219>255. 5 .
移项,合并同类项,得 x>36. 5.
由x应为正整数,得x≥37.
答:明年空气质量良好的天数比去年至少要增加
37,才能使这一年空气 质量良好的天数超过
全年天数的70%.
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的 优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收
费; 在乙商场累计购物超过50元后,超出50元
的部分按95%收费. 顾客到哪家 商场购物花费
少?
2
分析:
在甲商场购物超过100元后享受优惠,在乙商场
购物超过50元后享受优惠. 因此,我们需要分三
种情况讨论:
(1) 累计购物不超过50元;
(2) 累计购物超过50元而不超过100元;
(3) 累计购物超过100元.
解:
(1)当累计购物不超过50元时,在甲、乙两商场
购物都不享受优惠, 且两商场以同样价格出
售同样的商品,因此到两商场购物花费一样.
当累计购物超过50元而不超过100元时,享
受乙商场的购物优惠, 不享受甲商场的购物
优惠,因此到乙商场购物花费少.
(3)当累计购物超过100元时,设累计购物
x(x>100)元.
①若到甲商场购物花费少,则
50+0. 95(x-50)>100+0. 9(x-100).
解得x>150.
这就是说,累计购物超过150元时,到甲商场
购物花费少.
②若到乙商场购物花费少,则
50+0. 95(x-50)<100+0. 9(x-100).
解得x<150.
这就是说,累计购物超过100元而不到150元时,
到乙商场购物花费少.
③若50+0. 95(x-50)=100+0. 9(x-100),
解得x=150.
这就是说,累计购物为150元时,到甲、乙两
商场购物花费一样.
某物流公司,要将300吨物资运往某地,现有A,B两种型号的车可供调用,已知A型车每辆可装20吨,B型车每辆可装15吨,在每辆车不超载的条件下,把300吨物资装运完,问:在已确定调用5辆A型车的前提下至少还需调用B型车多少辆?
3
导引:
本题有一个不等关系,那就是A,B两种型号的
汽车总共调运的物资的吨数必须不少于300吨,
根据这个不等关系,列出一个一元一次不等式,
求出调用B型车辆数的范围.最后根据车辆数必
须为整数,得出B型车的辆数.
解:
设还需要B型车x辆.
根据题意,得20×5+15x≥300.
解得x≥13 .
由于x是车的辆数,应为正整数,
所以x的最小值为14.
答:至少还需调用B型车14辆.
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
总结归纳
3个小组方案在10天内生产500件产品〔每天生产量相同〕,按原先的生产速度,不能完成任务;如果每个小组每天比原先生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
合作与交流
二、一元一次不等式(组)的应用
解:设每个小组原先每天生产x件产品,由题意,得
3×10x<500,
3×10(x+1)>500
解不等式组,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
列一元一次不等式组解实际问题的一般步骤:
〔1〕审题;
〔2〕设未知数,找不等量关系;
〔3〕根据不等关系列不等式组;
〔4〕解不等式组;
〔5〕检验并作答.
总结归纳
例1:有假设干学生参加夏令营活动,晚上在一宾馆住宿
时,如果每间住4个,那么还有20人住不下,相同
的房间,如果每间住8人,那么还有一间住不满也
不空,请问:这群学生有多少人?有多少房间供
他们住?
解 设有x间房供他们住,那么学生有〔4x+20)人,
由题意,得
解不等式组,得5根据题意,x的值应是整数,所以x=6.
4x+20=44人.
答:有学生44人,有6间房供他们住.
(4x+20)-8(x-1)>0,
(4x+20)-8(x-1)<8.
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例2 用假设干辆载重量为 8 t 的汽车运一批货物,假设每辆汽车只装 4 t ,那么剩下 20 t 货物;假设每辆汽车装满 8 t,那么最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,那么这批货物共有〔4x+20 〕t.依题意得
解不等式组,得5<x <7.
小结
分析已知量、未知量及它们之间的关系,找出题目中的不等关系.
审
设出合适的未知数.
设
根据题中的不等关系列出不等式组.
列
解不等式组,求出其解集.
解
检验所求出的不等式组的解集是否符合题意.
验
写出答案.
答
用一元一次不等式组解决实际问题的步骤
1.红星商店计划用不超过 4200 元的资金,购进甲、乙两种单价分别为 60 元、100 元的商品共 50 件,据市场行情,销售甲、乙商品各一件分别可获利 10 元、20 元,两种商品均售完,若所获利润大于 750 元,则该店进货方案有( )
A.3种 B.4种
C.5种 D.6种
课堂练习
解析:设该店购进甲种商品 x 件,则购进乙种商品(50-x)件.
由题意得
解得 20≤ x<25.
∵ x 为整数,∴ x=20,21,22,23,24.
∴ 该店进货方案有 5 种.
2.为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 清理养鱼网箱人数/人 清理捕鱼网箱人数/人 总支出/元
A 15 9 57000
B 10 16 68000
(1)若两村清理同类渔具的人均支出费用一样,清理养鱼网箱和捕鱼网箱的人均支出费用分别是多少元?
解:(1)设清理养鱼网箱和捕鱼网箱的人均支出费用分别为 x 元、y 元.
根据题意,得
解得
答:清理养鱼网箱和捕鱼网箱的人均支出费用分别为 2000 元、3000 元.
(2)在人均支出费用不变的情况下,为节约开支,两村准备协调 40 人共同清理养鱼网箱和捕鱼网箱.要使总支出不超过 102000 元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
解:(2)设分配 a 人清理养鱼网箱,则分配(40-a)人清理捕鱼网箱.
根据题意,得
解得 18 ≤ a<20.
∵ a 为正整数,∴ a=18 或 19.
∴ 一共有 2 种分配方案,分别为:
方案一:分配 18 人清理养鱼网箱、22 人清理捕鱼网箱;
方案二:分配 19 人清理养鱼网箱、21 人清理捕鱼网箱.
某校组织学生参加“周末郊游”.甲旅行社说:“只要一名同学买全票,则其余学生可享受半价优惠.”乙旅行社说:“全体同学都可按6折优惠.”已知全票价为240元.
(1)设学生数为x,甲旅行社收费为y甲元,乙旅行
社收费为y乙元,用含x的代数式表述出y甲与
y乙的值;
(2)讨论哪一家旅行社更优惠.
3.
导引:
(1)根据题意直接列式、化简即可;(2)分三种情
况讨论:y甲>y乙,y甲=y乙,y甲<y乙,求满足要
求的学生数.
解:
(1)y甲=240+(x-1)×120=120x+120,
y乙=240×0.6x=144x.
(2)当y甲>y乙时,120x+120>144x,解得x<5.
∴当学生数少于5人时,乙旅行社更优惠.
当y甲=y乙时,120x+120=144x,解得x=5.
∴当学生数正好为5人时,两家旅行社一样优惠.
当y甲<y乙时,120x+120<144x,解得x>5.
∴当学生数超过5人时,甲旅行社更优惠.
4.今年秋天,某市某村水果喜获丰收,果农王灿收获枇杷 20吨、桃子 12 吨.现计划租用甲、乙两种货车共 8 辆,将这批水果全部运往外地销售.已知一辆甲种货车可装枇杷 4 吨和桃子 1 吨,一辆乙种货车可装枇杷和桃子各 2 吨.
(1)王灿如何安排甲、乙两种货车可一次性将这批水果运到销售地?有几种方案?
解:(1)设安排甲种货车 x 辆,则安排乙种货车 (8-x) 辆.
根据题意,得
解不等式组,得 2≤x≤4.
∵ x 是正整数,∴ x 可取的值为 2,3,4.
∴ 安排甲、乙两种货车有三种方案,如下表:
甲种货车 乙种货车
方案一 2辆 6辆
方案二 3辆 5辆
方案三 4辆 4辆
(2)若甲种货车每辆需付运输费 300 元,乙种货车每辆需付运输费 240 元,则果农王灿选择哪种方案可使运输费最少?最少运输费是多少?
解:(2)根据题意,可得
方案一所需运输费为 300×2+240×6= 2040(元);
方案二所需运输费为 300×3+240×5 =2100(元);
方案三所需运输费为 300×4+240×4 =2160(元).
∵ 2040<2100<2160,
∴ 王灿选择方案一可使运输费最少,最少运输费是 2040 元.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版八年级下册数学
第二章 一元一次不等式与一元一次不等式组
2.6.2一元一次不等式(组)的应用
一元一次方程解实际问题的步骤 :
实际问题
设未知数
找相等关系
列出方程
检验解的合理性
解方程
交流 : 那么如何用一元一次不等式解实际问题呢 ?
复习引入
一、一元一次不等式的应用
小华打算在星期天与同学去登山 , 计划上午7点出发 , 到达山顶后休息2h , 下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h , 回来时的平均速度是4km/h , 他们最远能登上哪座山顶〔图中数字表示出发点到山顶的路程〕 ?
前面问题中涉及的数量关系是 :
去时所花时间+休息时间+回来所花时间≤总时间.
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h,回来所花时间为 h.
他们在山顶休息了2 h , 又上午7点到下午4点之间总共相隔9 h , 即所用时间应小于或等于9 h.
所以有 +2+ ≤ 9.
解得 x≤12.
因此要满足下午4点以前必须返回出发点 , 小华他们最远能登上D山顶.
x ≥ 125.
例1 某童装店按每套90元的价格购进40套童装 , 应缴纳的税费为销售额的10%. 如果要获得900元的纯利润 , 每套童装的售价至少是多少元 ?
解 : 设每套童装的售价是 x 元.
那么 40x-90×40-40x·10%≥900.
解得
答 : 每套童装的售价至少是125元.
分析 : 此题涉及的数量关系是 :
销售额-成本-税费≥纯利润(900元).
典例精析
例2 当一个人坐下时 , 不宜提举超过4.5 kg的重物 , 以免受伤. 小明坐在书桌前 , 桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本 ?
解: 设小明应搬动x本记事本 , 那么
解得 x≤5.25.
x≤4.5.
答 : 小明最多只应搬动5本记事本.
由于记事本的数目必须是整数 , 所以x 的最大值为5.
解:设小明家每月用水x立方米.
∵5×1.8=9<15 ,
∴小明家每月用水超过5立方米 ,
那么超出(x-5)立方米 , 按每立方米2元收费 ,
列出不等式为 : 5×1.8+(x-5)×2≥15 ,
解不等式得 : x≥8.
答 : 小明家每月用水量至少是8立方米.
例3 小明家每月水费都不少于15元 , 自来水公司的收费标准如下 : 假设每户每月用水不超过5立方米 , 那么每立方米收费1.8元 ; 假设每户每月用水超过5立方米 , 那么超出部分每立方米收费2元 , 小明家每月用水量至少是多少 ?
例4 甲、乙两超市以同样价格出售同样的商品 , 并且给出了差别的优惠方案 : 在甲超市累计购物超过100元后 , 超出100元的部分按90%收费 ; 在乙超市累计购物超过50元后 , 超出50元的部分按95%收费. 顾客到哪家超市购物花费少 ?
分析:甲乙两超市的优惠价格不一样 , 因此需要分类讨论 :
(1)当购物不超过50元 ;
(2)当购物超过50元而不超过100元,
(3)当购物超过100元.
解:(1)当购物不超过50元时,在甲、乙两超市都不享受优惠 , 购物花费一样 ;
(2)当购物超过50元而不超过100元时,在乙超市享受优惠 , 购物花费少;
(3)当累计购物超过100元后 , 设购物为x(x>100)元
①假设 50+0.95(x-50)>100+0.9(x-100) 即x>150
在甲超市购物花费少;
②假设 50+0.95(x-50)<100+0.9(x-100) 即x<150
在乙超市购物花费少;
③假设 50+0.95(x-50)=100+0.9(x-100) 即x=150
在甲、乙两超市购物花费一样.
去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%. 那么明年空气质量良好的天数比去年至少要增加多少?
1
分析:
“明年这样的比值要超过70%”指出了这个问題
中蕴含的不等关系. 转化为不等式,即
练一练
解:
设明年比去年空气质量良好的天数增加了x.
去年有365×60%天空气质量良好,明年有
(x+365×60%)天空气质量良好,并且
去分母,得 x+219>255. 5 .
移项,合并同类项,得 x>36. 5.
由x应为正整数,得x≥37.
答:明年空气质量良好的天数比去年至少要增加
37,才能使这一年空气 质量良好的天数超过
全年天数的70%.
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的 优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收
费; 在乙商场累计购物超过50元后,超出50元
的部分按95%收费. 顾客到哪家 商场购物花费
少?
2
分析:
在甲商场购物超过100元后享受优惠,在乙商场
购物超过50元后享受优惠. 因此,我们需要分三
种情况讨论:
(1) 累计购物不超过50元;
(2) 累计购物超过50元而不超过100元;
(3) 累计购物超过100元.
解:
(1)当累计购物不超过50元时,在甲、乙两商场
购物都不享受优惠, 且两商场以同样价格出
售同样的商品,因此到两商场购物花费一样.
当累计购物超过50元而不超过100元时,享
受乙商场的购物优惠, 不享受甲商场的购物
优惠,因此到乙商场购物花费少.
(3)当累计购物超过100元时,设累计购物
x(x>100)元.
①若到甲商场购物花费少,则
50+0. 95(x-50)>100+0. 9(x-100).
解得x>150.
这就是说,累计购物超过150元时,到甲商场
购物花费少.
②若到乙商场购物花费少,则
50+0. 95(x-50)<100+0. 9(x-100).
解得x<150.
这就是说,累计购物超过100元而不到150元时,
到乙商场购物花费少.
③若50+0. 95(x-50)=100+0. 9(x-100),
解得x=150.
这就是说,累计购物为150元时,到甲、乙两
商场购物花费一样.
某物流公司,要将300吨物资运往某地,现有A,B两种型号的车可供调用,已知A型车每辆可装20吨,B型车每辆可装15吨,在每辆车不超载的条件下,把300吨物资装运完,问:在已确定调用5辆A型车的前提下至少还需调用B型车多少辆?
3
导引:
本题有一个不等关系,那就是A,B两种型号的
汽车总共调运的物资的吨数必须不少于300吨,
根据这个不等关系,列出一个一元一次不等式,
求出调用B型车辆数的范围.最后根据车辆数必
须为整数,得出B型车的辆数.
解:
设还需要B型车x辆.
根据题意,得20×5+15x≥300.
解得x≥13 .
由于x是车的辆数,应为正整数,
所以x的最小值为14.
答:至少还需调用B型车14辆.
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
总结归纳
3个小组方案在10天内生产500件产品〔每天生产量相同〕,按原先的生产速度,不能完成任务;如果每个小组每天比原先生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
合作与交流
二、一元一次不等式(组)的应用
解:设每个小组原先每天生产x件产品,由题意,得
3×10x<500,
3×10(x+1)>500
解不等式组,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
列一元一次不等式组解实际问题的一般步骤:
〔1〕审题;
〔2〕设未知数,找不等量关系;
〔3〕根据不等关系列不等式组;
〔4〕解不等式组;
〔5〕检验并作答.
总结归纳
例1:有假设干学生参加夏令营活动,晚上在一宾馆住宿
时,如果每间住4个,那么还有20人住不下,相同
的房间,如果每间住8人,那么还有一间住不满也
不空,请问:这群学生有多少人?有多少房间供
他们住?
解 设有x间房供他们住,那么学生有〔4x+20)人,
由题意,得
解不等式组,得5
4x+20=44人.
答:有学生44人,有6间房供他们住.
(4x+20)-8(x-1)>0,
(4x+20)-8(x-1)<8.
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例2 用假设干辆载重量为 8 t 的汽车运一批货物,假设每辆汽车只装 4 t ,那么剩下 20 t 货物;假设每辆汽车装满 8 t,那么最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,那么这批货物共有〔4x+20 〕t.依题意得
解不等式组,得5<x <7.
小结
分析已知量、未知量及它们之间的关系,找出题目中的不等关系.
审
设出合适的未知数.
设
根据题中的不等关系列出不等式组.
列
解不等式组,求出其解集.
解
检验所求出的不等式组的解集是否符合题意.
验
写出答案.
答
用一元一次不等式组解决实际问题的步骤
1.红星商店计划用不超过 4200 元的资金,购进甲、乙两种单价分别为 60 元、100 元的商品共 50 件,据市场行情,销售甲、乙商品各一件分别可获利 10 元、20 元,两种商品均售完,若所获利润大于 750 元,则该店进货方案有( )
A.3种 B.4种
C.5种 D.6种
课堂练习
解析:设该店购进甲种商品 x 件,则购进乙种商品(50-x)件.
由题意得
解得 20≤ x<25.
∵ x 为整数,∴ x=20,21,22,23,24.
∴ 该店进货方案有 5 种.
2.为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 清理养鱼网箱人数/人 清理捕鱼网箱人数/人 总支出/元
A 15 9 57000
B 10 16 68000
(1)若两村清理同类渔具的人均支出费用一样,清理养鱼网箱和捕鱼网箱的人均支出费用分别是多少元?
解:(1)设清理养鱼网箱和捕鱼网箱的人均支出费用分别为 x 元、y 元.
根据题意,得
解得
答:清理养鱼网箱和捕鱼网箱的人均支出费用分别为 2000 元、3000 元.
(2)在人均支出费用不变的情况下,为节约开支,两村准备协调 40 人共同清理养鱼网箱和捕鱼网箱.要使总支出不超过 102000 元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
解:(2)设分配 a 人清理养鱼网箱,则分配(40-a)人清理捕鱼网箱.
根据题意,得
解得 18 ≤ a<20.
∵ a 为正整数,∴ a=18 或 19.
∴ 一共有 2 种分配方案,分别为:
方案一:分配 18 人清理养鱼网箱、22 人清理捕鱼网箱;
方案二:分配 19 人清理养鱼网箱、21 人清理捕鱼网箱.
某校组织学生参加“周末郊游”.甲旅行社说:“只要一名同学买全票,则其余学生可享受半价优惠.”乙旅行社说:“全体同学都可按6折优惠.”已知全票价为240元.
(1)设学生数为x,甲旅行社收费为y甲元,乙旅行
社收费为y乙元,用含x的代数式表述出y甲与
y乙的值;
(2)讨论哪一家旅行社更优惠.
3.
导引:
(1)根据题意直接列式、化简即可;(2)分三种情
况讨论:y甲>y乙,y甲=y乙,y甲<y乙,求满足要
求的学生数.
解:
(1)y甲=240+(x-1)×120=120x+120,
y乙=240×0.6x=144x.
(2)当y甲>y乙时,120x+120>144x,解得x<5.
∴当学生数少于5人时,乙旅行社更优惠.
当y甲=y乙时,120x+120=144x,解得x=5.
∴当学生数正好为5人时,两家旅行社一样优惠.
当y甲<y乙时,120x+120<144x,解得x>5.
∴当学生数超过5人时,甲旅行社更优惠.
4.今年秋天,某市某村水果喜获丰收,果农王灿收获枇杷 20吨、桃子 12 吨.现计划租用甲、乙两种货车共 8 辆,将这批水果全部运往外地销售.已知一辆甲种货车可装枇杷 4 吨和桃子 1 吨,一辆乙种货车可装枇杷和桃子各 2 吨.
(1)王灿如何安排甲、乙两种货车可一次性将这批水果运到销售地?有几种方案?
解:(1)设安排甲种货车 x 辆,则安排乙种货车 (8-x) 辆.
根据题意,得
解不等式组,得 2≤x≤4.
∵ x 是正整数,∴ x 可取的值为 2,3,4.
∴ 安排甲、乙两种货车有三种方案,如下表:
甲种货车 乙种货车
方案一 2辆 6辆
方案二 3辆 5辆
方案三 4辆 4辆
(2)若甲种货车每辆需付运输费 300 元,乙种货车每辆需付运输费 240 元,则果农王灿选择哪种方案可使运输费最少?最少运输费是多少?
解:(2)根据题意,可得
方案一所需运输费为 300×2+240×6= 2040(元);
方案二所需运输费为 300×3+240×5 =2100(元);
方案三所需运输费为 300×4+240×4 =2160(元).
∵ 2040<2100<2160,
∴ 王灿选择方案一可使运输费最少,最少运输费是 2040 元.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
