华东师大版七年级下册数学 9.2 多边形的内角和课件 (共20张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 9.2 多边形的内角和课件 (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
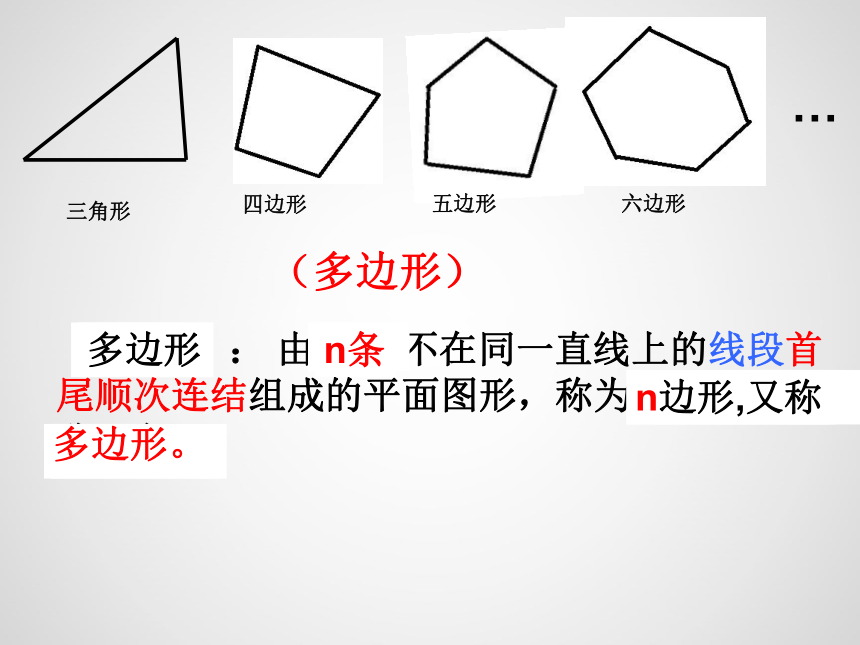
(多边形)
…
三角形
四边形
五边形
六边形
: 由 三条不在同一直线上的线段首尾顺次连结组成的平面图形,称为三边形,又称三角形。
三角形
四边形
四条
四边形
五边形
五条
五边形
多边形。
n边形,又称
n条
多边形
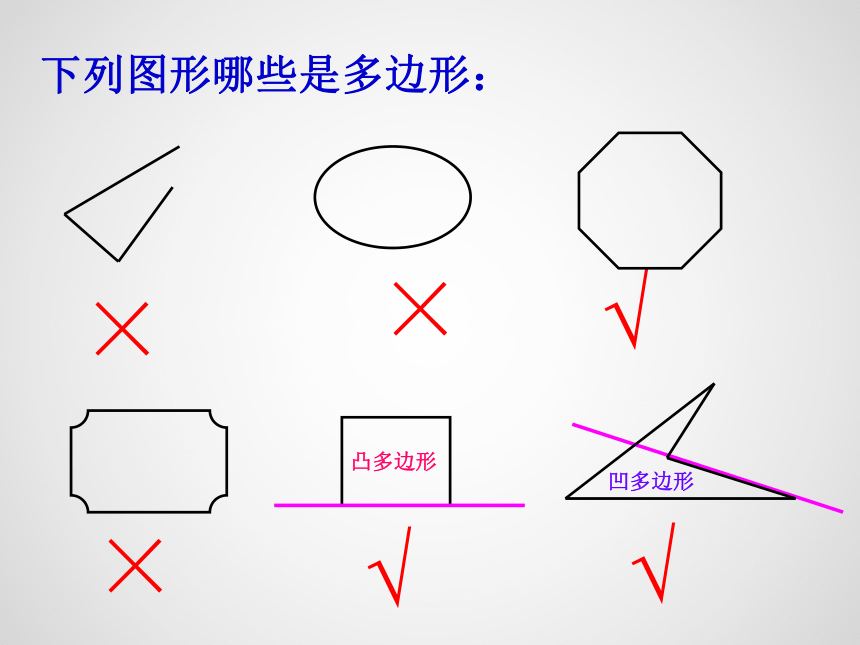
下列图形哪些是多边形:
√
×
×
×
√
√
凸多边形
凹多边形
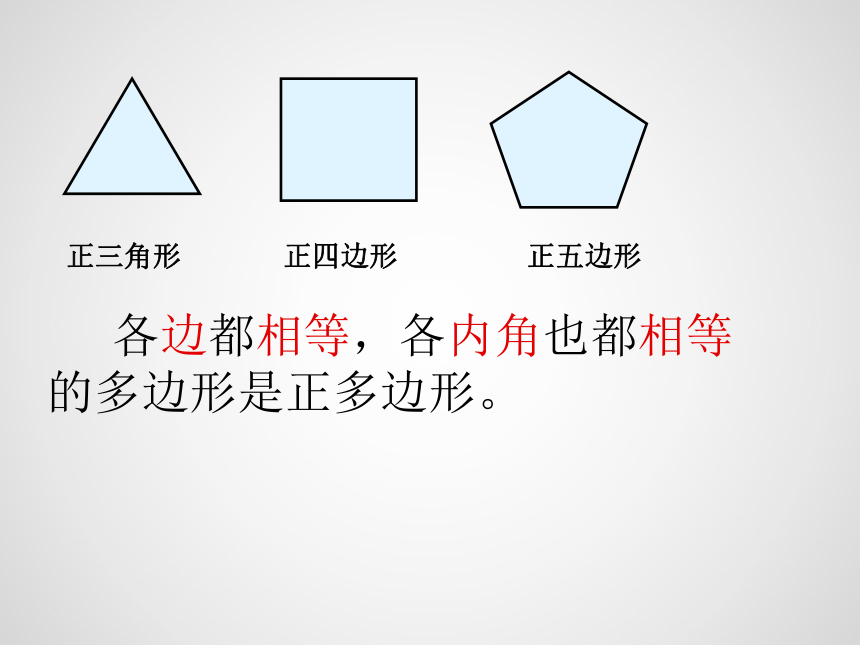
正三角形
正四边形
正五边形
各边都相等,各内角也都相等的多边形是正多边形。
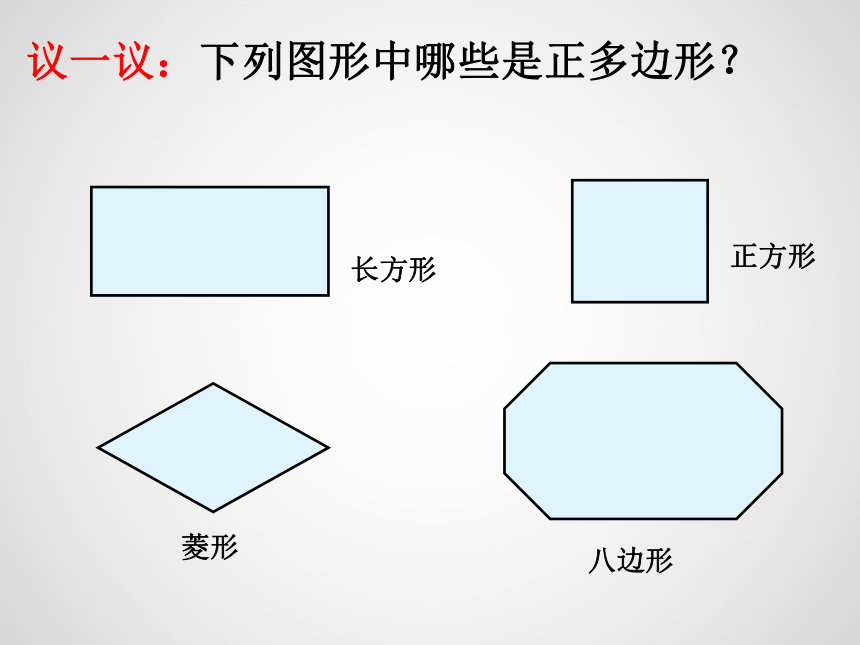
议一议:下列图形中哪些是正多边形?
长方形
八边形
菱形
正方形
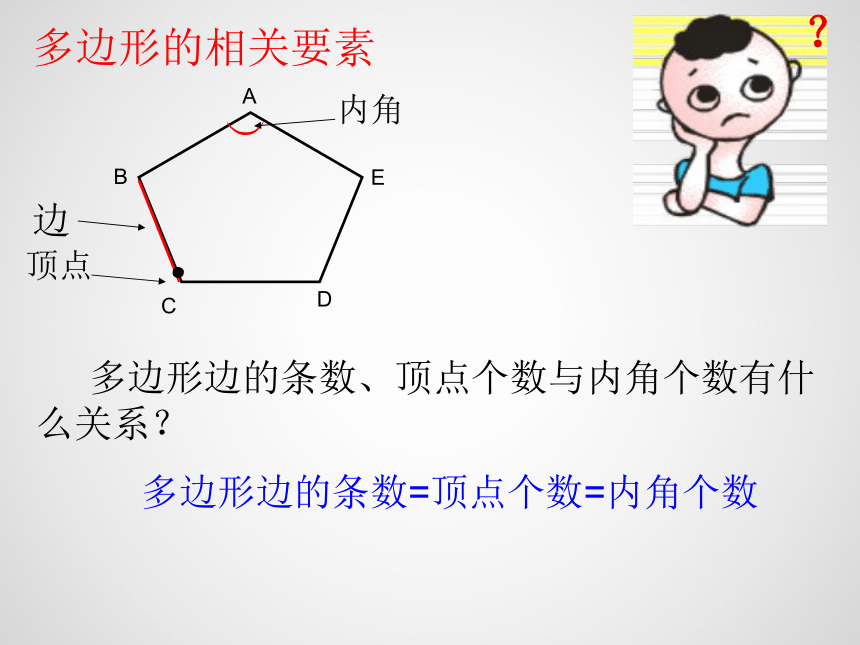
多边形的相关要素
.
(
边
顶点
内角
多边形边的条数、顶点个数与内角个数有什么关系?
多边形边的条数=顶点个数=内角个数
?
A
B
C
D
E
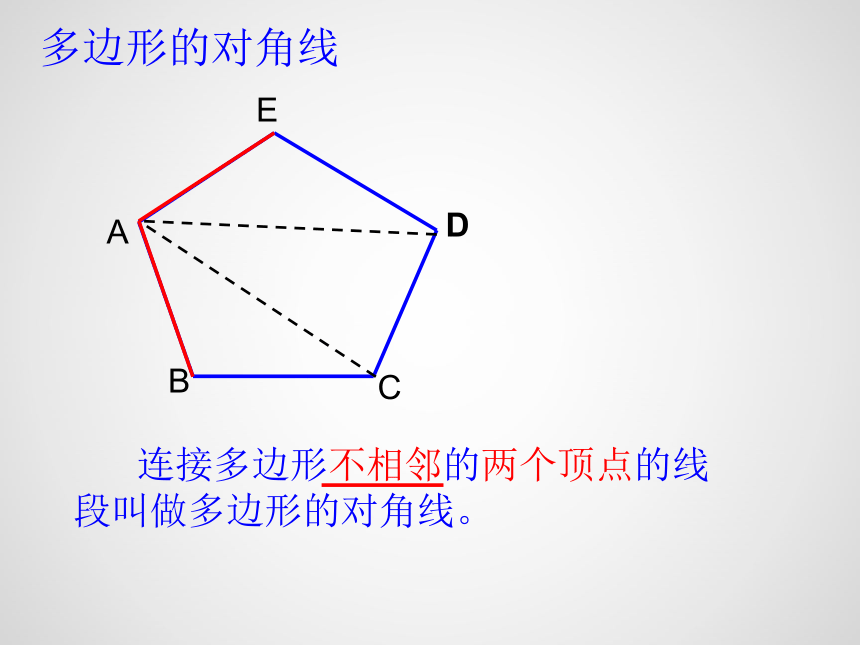
多边形的对角线
B
A
C
D
E
连接多边形不相邻的两个顶点的线段叫做多边形的对角线。
多边形 三角形 四边形 五边形 六边形 … n边形
从一个顶点引出对角线条数 …
多边形的内角和 …
分成三角形的个数 …
1
n-3
0
4×180° = 720°
3×180°=540°
2×180° = 360°
180°
n-2
4
2
3
(n-2)×180°
C
B
A
D
C
B
A
E
D
C
B
A
E
D
C
B
A
F
1
2
3
分别画出从三角形、四边形、五边形、六边形的一个顶点出发的所有对角线.
探索多边形的内角和
多边形的内角和为:
(n-2)·180°
总结:
多边形的内角和与边数有关,当边数每增加一边时,内角和就增加180°,也就是说多边形的内角和一定是180°的正整数倍。
(n≥3的整数)
抢答:
3、判断下列数据中哪个是多边形的内角和( ).
A.560° B.1000° C.780° D.1800°
D
1、过一个多边形的一个顶点有7条对角线,则这是 边形.
十
2、过一个多边形的一个顶点的所有对角线将这个多边形分成五个三角形,则是 边形.
七
多边形 四边形 六边形 八边形 十边形 十一边形
从一个顶点引出对角线条数 7
分成三角形个数 6
多边形内角和 360°
练习
完成下表:
多边形 四边形 六边形 八边形 十边形 十一边形
从一个顶点引出对角线条数 1 3 5 7 9
分成三角形个数 2 4 6 8 10
多边形内角和 360° 720° 1080° 1440° 1800°
练习
完成下表:
已知一个多边形内角和等于2340 ,求它的边数。
练一练,看你学得怎么样
如果一个正多边形的一个内角等于120°,则这个多边形的边数是多少?
巩固练习
畅所欲言、分享成果
这节课我学会了……
平面图形的密布
`
作业:
教材P86
练习第1、2题
从一个顶点出发可以引(n-3)条对角线,那么多边形一共用多少条对角线呢?
思考
(多边形)
…
三角形
四边形
五边形
六边形
: 由 三条不在同一直线上的线段首尾顺次连结组成的平面图形,称为三边形,又称三角形。
三角形
四边形
四条
四边形
五边形
五条
五边形
多边形。
n边形,又称
n条
多边形
下列图形哪些是多边形:
√
×
×
×
√
√
凸多边形
凹多边形
正三角形
正四边形
正五边形
各边都相等,各内角也都相等的多边形是正多边形。
议一议:下列图形中哪些是正多边形?
长方形
八边形
菱形
正方形
多边形的相关要素
.
(
边
顶点
内角
多边形边的条数、顶点个数与内角个数有什么关系?
多边形边的条数=顶点个数=内角个数
?
A
B
C
D
E
多边形的对角线
B
A
C
D
E
连接多边形不相邻的两个顶点的线段叫做多边形的对角线。
多边形 三角形 四边形 五边形 六边形 … n边形
从一个顶点引出对角线条数 …
多边形的内角和 …
分成三角形的个数 …
1
n-3
0
4×180° = 720°
3×180°=540°
2×180° = 360°
180°
n-2
4
2
3
(n-2)×180°
C
B
A
D
C
B
A
E
D
C
B
A
E
D
C
B
A
F
1
2
3
分别画出从三角形、四边形、五边形、六边形的一个顶点出发的所有对角线.
探索多边形的内角和
多边形的内角和为:
(n-2)·180°
总结:
多边形的内角和与边数有关,当边数每增加一边时,内角和就增加180°,也就是说多边形的内角和一定是180°的正整数倍。
(n≥3的整数)
抢答:
3、判断下列数据中哪个是多边形的内角和( ).
A.560° B.1000° C.780° D.1800°
D
1、过一个多边形的一个顶点有7条对角线,则这是 边形.
十
2、过一个多边形的一个顶点的所有对角线将这个多边形分成五个三角形,则是 边形.
七
多边形 四边形 六边形 八边形 十边形 十一边形
从一个顶点引出对角线条数 7
分成三角形个数 6
多边形内角和 360°
练习
完成下表:
多边形 四边形 六边形 八边形 十边形 十一边形
从一个顶点引出对角线条数 1 3 5 7 9
分成三角形个数 2 4 6 8 10
多边形内角和 360° 720° 1080° 1440° 1800°
练习
完成下表:
已知一个多边形内角和等于2340 ,求它的边数。
练一练,看你学得怎么样
如果一个正多边形的一个内角等于120°,则这个多边形的边数是多少?
巩固练习
畅所欲言、分享成果
这节课我学会了……
平面图形的密布
`
作业:
教材P86
练习第1、2题
从一个顶点出发可以引(n-3)条对角线,那么多边形一共用多少条对角线呢?
思考
